数据结构—散列表的查找
7.4散列表的查找
7.4.1散列表的基本概念
基本思想:记录的存储位置域关键字之间存在对应关系
对应关系——hash函数
Loc(i)= H(keyi)
如何查找:

根据散列函数 H(key) = k
查找key=9,则访问H(4)= 18号地址,若内容为18则成功;
若查不到,则返回一个特殊值,如空指针或空记录。
优点:查找效率高
缺点:空间效率低
7.4.2散列表的若干术语
散列方法(杂凑法):
选取某个函数,依该函数按关键字计算元素的存储位置,并按此存放;
查找时,由同一个函数对给定值K计算地址,将k与地址单元中元素关键码进行比,确定查找是否成功。
散列函数(杂凑函数):散列方法中使用的转换函数
散列表(杂凑表):按上述思想构造的表 散列函数:H(key)=k

冲突:不同的关键码映射到同一个散列地址 key1≠key2,但是H(key1)=H(key2)
例如:有6个元素的关键码分别为:(25,21,39,9,23,11)。
- 选取关键码与元素位置间的函数为H(k)=k mod 7,
- 地址编号从0-6
7.4.3散列函数的构造方法
散列存储:选取某个函数,依该函数按关键字计算元素的存储位置
Loc(i)=H(keyi)
在散列查找方法中,冲突是不可能避免的,只能尽可能减少。
使用散列表要解决好两个问题:
-
构造好的散列函数
a)所选函数尽可能简单,以便提高转换速度;
b)所选函数对关键码计算出的地址,应在散列地址集中致均匀分布,以减少空间浪费。
-
制定一个好的解决冲突的方案
查找时,如果从散列函数计算出的地址中查不到关键码,则应当依据解决冲突的规则,有规律地查询其他相关单元。
构造散列函数考虑的因素:
- 执行速度(即计算散列函数所需要的时间);
- 关键字的长度;
- 散列表的长度;
- 关键字的分布情况;
- 查找频率。
根据元素集合的特性构造
- 要求一:n 个数据源仅占用 n 个地址,虽然散列查找是以空间换时间,但仍希望散列的地址空间尽量小。
- 要求二:无论用什么方法存储,目的都是尽量均匀地存放元素,以避免冲突。
1、直接定址法
Hash(key)= a·key + b (a、b为常数)
优点:以关键码key的某个线性函数值为散列地址,不会产生冲突。
缺点:要占用连续地址空间,空间效率低。
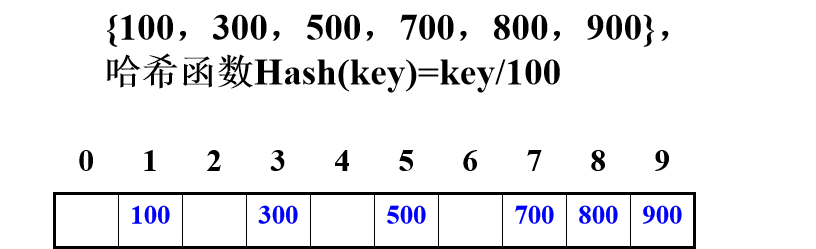
2、除留余数法
Hash(key)= key mod p(p是一个整数)
关键:如何选取合适的p?
技巧:设表长为m,取p≤m且为质数

7.4.4处理冲突的方法
1、开放地址法(开地址法)
基本思想:有冲突时就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将数据元素存入。
例如:除留余数法 Hi=(Hash(key)+di) mod m di为增量序列
常用方法:
线性探测法 di为1,2,…m-1线性序列 一旦冲突,就找下一个地址,直到找到空地址存入
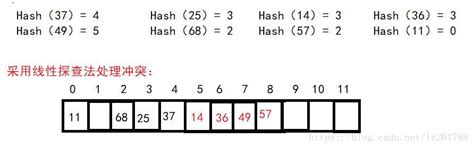
二次探测法 di为12,-12,22,-22,…,q2二次序列
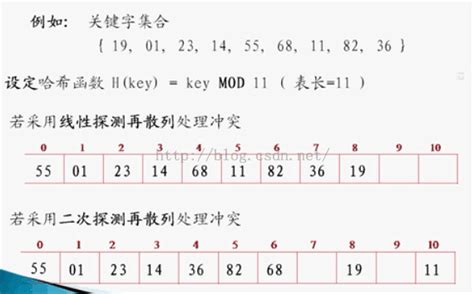
伪随机探测法 di为伪随机数序列
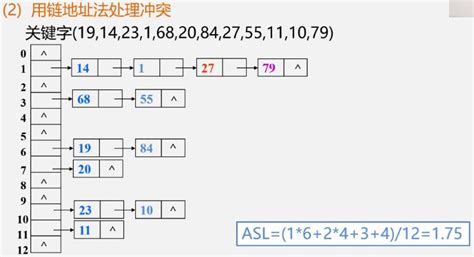
2、链地址法(拉链法)
基本思想:相同散列地址的记录链成一单链表
m个散列地址就设m个单链表,然后用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构。

链地址法建立散列表步骤:
- Step1:取数据元素的关键字key,计算其散列函数值(地址)。若该地址对应的链表为空,则将该元素插入此链表;否则执行Step2解决冲突。
- Step2:根据选择的冲突处理方法,计算关键字key的下一个存储地址。若该地址对应的链表不为空,则利用链表的前插法或后插法将该元素插入此链表。
链地址法的优点:
- 非同义词不会冲突,无聚集现象
- 链表上结点空间动态申请,更适合于表长不确定的情况
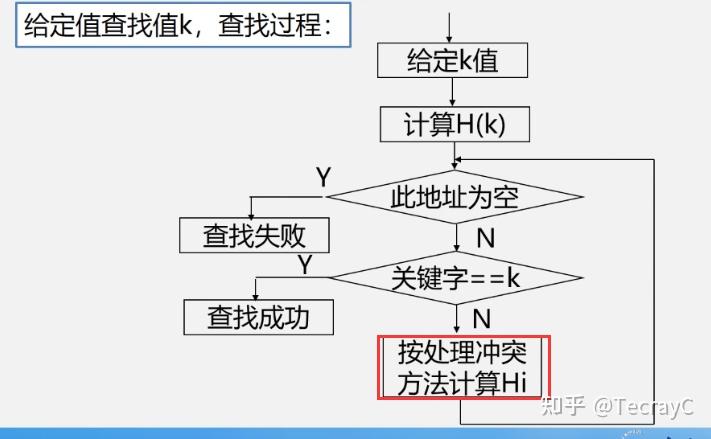
7.4.5散列表的查找
给定值查找值k,查找过程:
相关文章:

数据结构—散列表的查找
7.4散列表的查找 7.4.1散列表的基本概念 基本思想:记录的存储位置域关键字之间存在对应关系 对应关系——hash函数 Loc(i) H(keyi) 如何查找: 根据散列函数 H(key) k 查找key9,则访…...
Expo项目 使用Native base UI库
装包: yarn add native-base expo install react-native-svg12.1.1 Index.js: import React from react import { View, Text } from react-native import useList from ./useList import { NativeBaseProvider, Button, Box } from native-base import styles f…...
74、75、76——tomcat项目实战
tomcat项目实战 tomcat 依赖 java运行环境,必须要有jre , 选择 jdk1.8 JvmPertest 千万不能用 kyj易捷支付 项目机器 选择 一台机器 ,安装jdk1.8的机器下载tomcat的包 上传到机器,解压tomcattomcat文件 bin文件夹: 启动文件 堆栈配置文件 catalina.sh JAVA_OPTS="-Xm…...

jmeter errstr :“unsupported field type for multipart.FileHeader“
在使用jmeter测试接口的时候,提示errstr :"unsupported field type for multipart.FileHeader"如图所示 这是因为我们 在HTTP信息头管理加content-type参数有问题 直接在HTTP请求中,勾选: use multipart/form-data for POST【中文…...

C#调用C++ DLL传参byte[]数组字节值大于127时会变为0x3f的问题解决
最近做了一个网络编程的DLL给C#调用,DLL中封装了一个TCP Client的函数接口,如下所示 //C TCP报文发送接口 int TcpClient_send(unsigned char* buffSend, unsigned int nLen) {unsigned char buff[1024];int len StringToHex(buffSend, buff);int nRet…...
【vue3+xlxs+xlsx-style-vite】vue3项目中使用xlsx插件实现Excel表格的导出和解析,已实现
在vue3项目中使用xlsx插件实现Excel表格的导出和解析 1、xlsx插件包官方 xlsx插件包官方 2、FileReader官方文档:FileReader官方文档 安装xlsx和xlsx-style-vite、file-saver npm install xlsx npm install xlsx-style-vite npm install file-saverpackage.json中查…...

Doris2.0时代的一些机遇和挑战!
300万字!全网最全大数据学习面试社区等你来! 上个周五的时候,Doris官宣了2.0版本,除了在性能上的大幅提升,还有一些特性需要大家特别关注。 根据官网的描述,Doris在下面领域都有了长足进步: 日志…...
Leetcode-每日一题【剑指 Offer 32 - I. 从上到下打印二叉树】
题目 从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。 例如: 给定二叉树: [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回: [3,9,20,15,7] 提示: 节点总数 < 1000 解题思路 1.题目要求我们从…...
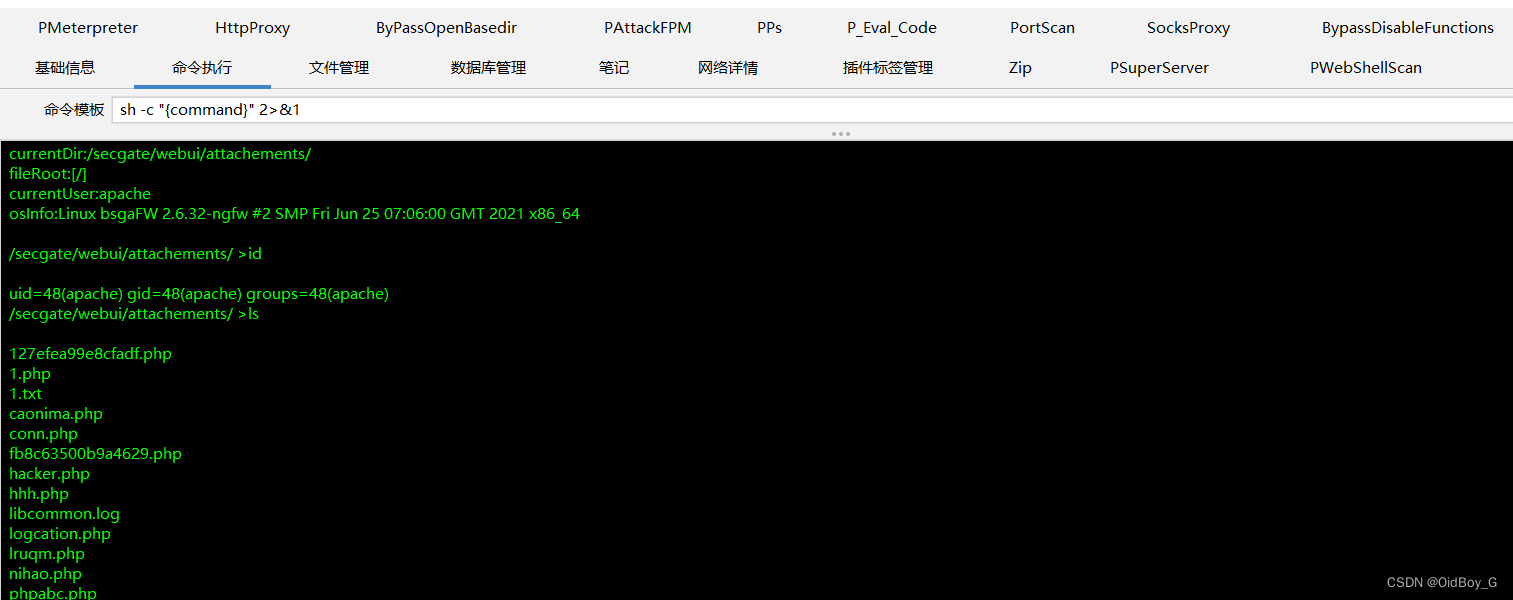
网神 SecGate 3600 防火墙任意文件上传漏洞复现
0x01 产品简介 网神SecGate3600下一代极速防火墙(NSG系列)是基于完全自主研发、经受市场检验的成熟稳定网神第三代SecOS操作系统 并且在专业防火墙、VPN、IPS的多年产品经验积累基础上精心研发的高性能下一代防火墙 专门为运营商、政府、军队、教育、大型…...

把独显塞回CPU,新核显能够媲美RTX 30、40系显卡了
上个月,AMD 发布了 Zen4 架构 R5 7600X 的无核显版 - 7500F 。 各种数据评测和玩家实际体验大家也已经看过了,说是变相降价一点不错。 原因也很简单,感谢 Intel 。 Jon Peddie Research 刚出炉报告显示,2023 第二季度 AMD 客户端…...
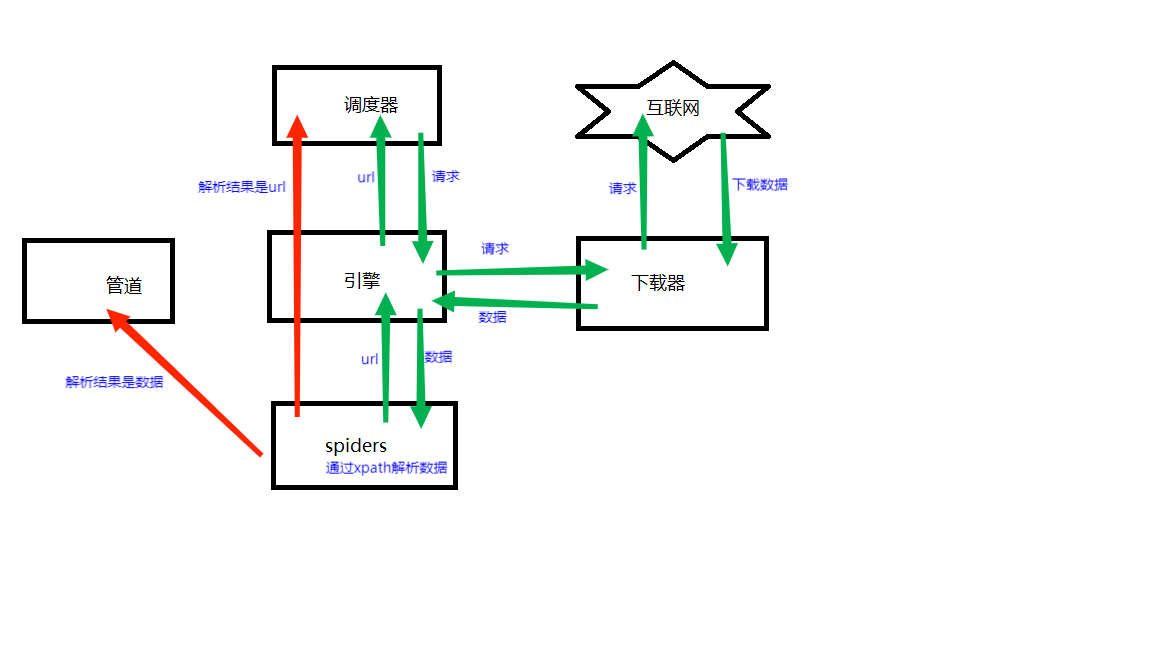
Python爬虫——scrapy_工作原理
引擎向spiders要url引擎把将要爬取的url给调度器调度器会将url生成的请求对象放入到指定的队列中从队列中出队一个请求引擎将请求交给下载器进行处理下载器发送请求获取互联网数据下载器将数据返回给引擎引擎将数据再次给到spidersspiders通过xpath解析该数据,得到数…...
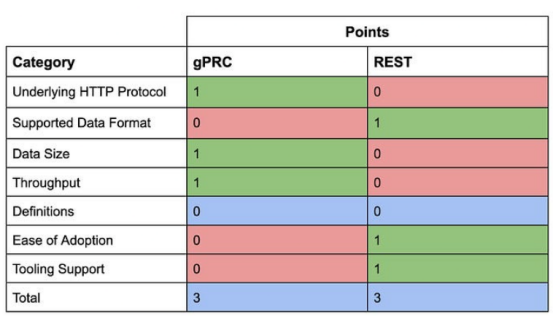
gRPC vs REST:创建API的方法比较
本文对gRPC和REST的特征和区别进行了介绍,这可能是当今创建API最常用的两种方法。 文章目录 一、gRPC的介绍 二、什么是REST? 三、什么是gRPC? 四、gRPC和REST的比较 (1)底层HTTP协议 (2)支持的数据…...
缓存平均的两种算法
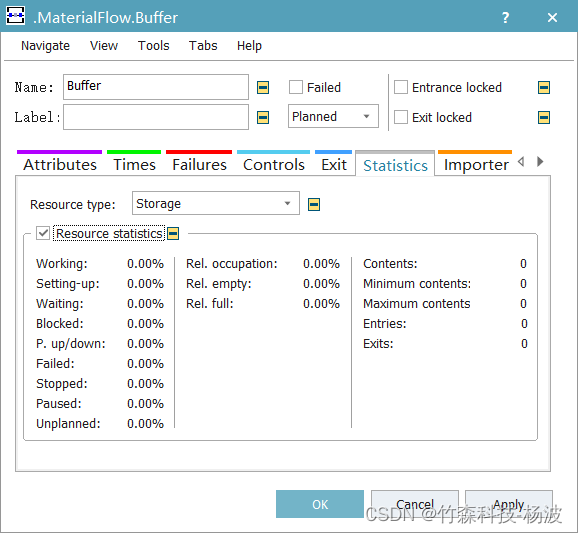
引言 线边库存物料的合理性问题是物流仿真中研究的重要问题之一,如果线边库存量过多,则会对生产现场的布局产生负面影响,增加成本,降低效益。 写在前面 仿真分析后对线边Buffer的使用情况进行合理的评估就是一个非常重要的事情。比较关心的参数包括:缓存位最大值…...
SpringBoot的配置文件(properties与yml)
文章目录 1. 配置文件的作用2. 配置文件格式3. 配置文件的使用方法3.1. properties配置文件3.1.1. 基本语法和使用3.1.2. properties优缺点分析 3.2. yml配置文件3.2.1. 基本语法与使用3.2.2. yml中单双引号问题3.2.3. yml配置不同类型的数据类型及null3.2.4. 配置对象3.2.5. 配…...
如何应用项目管理软件进行敏捷开发管理
敏捷开发(Agile Development)是一种软件开发方法论,强调在不断变化的需求和环境下,通过迭代、协作和自适应的方式来开发软件。敏捷方法的目标是提供更快、更灵活、更高质量的软件交付,以满足客户需求并实现项目成功。 …...

ARM DIY 硬件调试
前言 之前打样的几块 ARM 板,一直放着没去焊接。今天再次看到,决定把它焊起来。 加热台焊接 为了提高焊接效率,先使用加热台焊接。不过板子为双面贴片,使用加热台只能焊接一面,那就优先焊主芯片那面,并…...
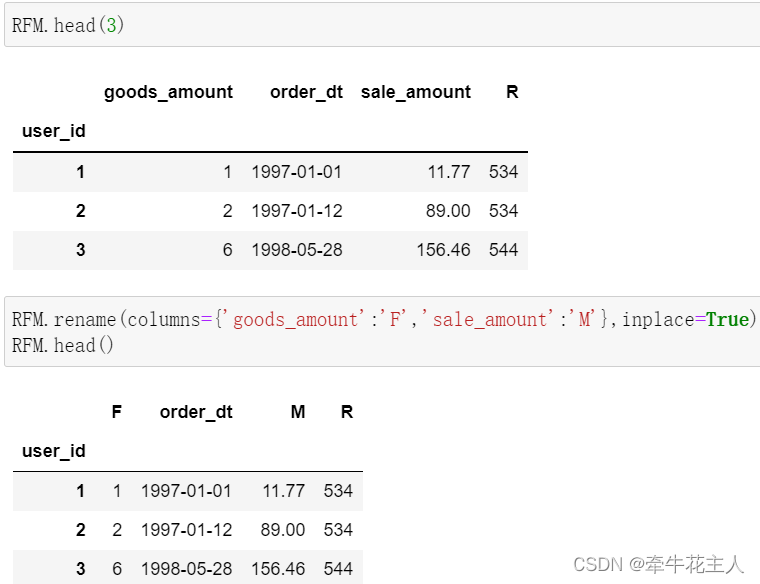
DataFrame.rename()函数--Pandas
1. 函数作用 修改DataFrame的行名、列名 2. 函数语法 DataFrame.rename(mapperNone, *, indexNone, columnsNone, axisNone, copyNone, inplaceFalse, levelNone, errorsignore)3. 函数参数 参数含义mapper与axis结合使用,表示运用到axis上的值:类字…...

09- DMA(DirectMemoryAccess直接存储器访问)
DMA 09 、DMA(DirectMemoryAccess直接存储器访问)DMA配置流程 09 、DMA(DirectMemoryAccess直接存储器访问) DMA配置流程 dma.c文件 main.c文件 详见《stm32中文参考手册》表57。...
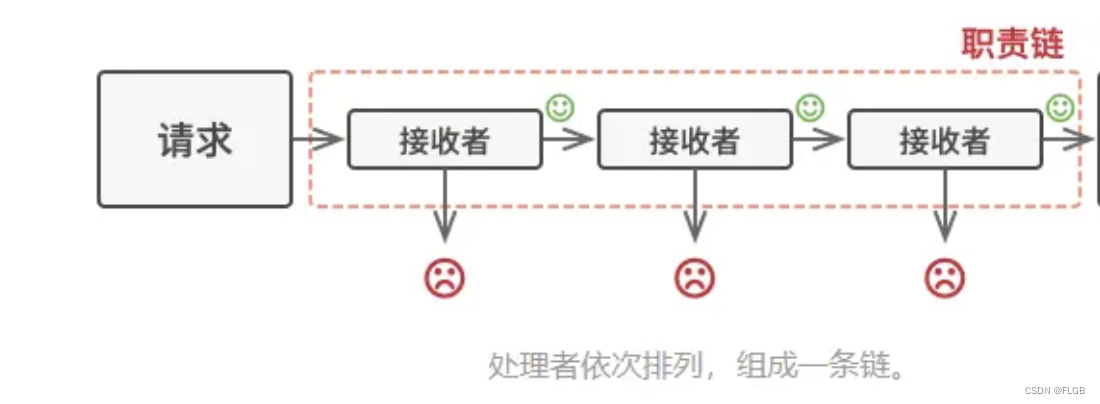
责任链模式
责任链模式 责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,它用于将请求的发送者和接收者解耦,使多个对象都有机会处理请求。这种模式建立在一个处理对象的链上,每个处理对象都可以选择处理请求或…...

【BI看板】Docker-compose安装Superset,安装最新版本2.1.0
软件及环境准备 docker, docker-compose docker-compose安装 字节码安装 #wget https://github.com/docker/compose/releases/download/v2.5.0/docker-compose-linux-x86_64 #mv docker-compose-linux-x86_64 docker-compose #chmod x /usr/local/bin/docker-com…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
