(搜索) 剑指 Offer 12. 矩阵中的路径 ——【Leetcode每日一题】
❓剑指 Offer 12. 矩阵中的路径
难度:中等
给定一个 m * n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如,在下面的 3×4 的矩阵中包含单词 "ABCCED"(单词中的字母已标出)。
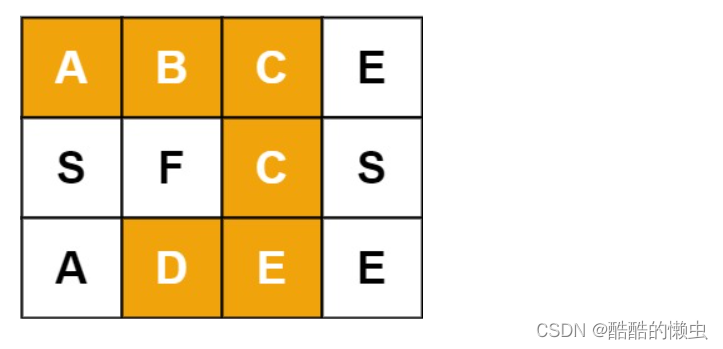
示例 1:
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出:true
示例 2:
输入:board = [[“a”,“b”],[“c”,“d”]], word = “abcd”
输出:false
提示:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15board和word仅由大小写英文字母组成
注意:本题 79. 单词搜索 相同。
💡思路:回溯法
使用回溯法(backtracking)进行求解,它是一种暴力搜索方法,通过搜索所有可能的结果来求解问题。
回溯法在一次搜索结束时需要进行回溯(回退),将这一次搜索过程中设置的状态进行清除,从而开始一次新的搜索过程。
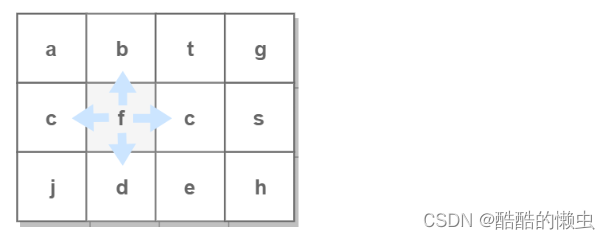
例如下图示例中,从 f 开始,下一步有 4 种搜索可能,
- 如果先搜索
b,需要将b标记为已经使用,防止重复使用。 - 在这一次搜索结束之后,需要将
b的已经使用状态清除,并搜索c。
🍁代码:(C++、Java)
C++
class Solution {
private:vector<pair<int, int>> dirs{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};int m, n;bool check(vector<vector<char>>& board, vector<vector<int>>& visited, int i, int j, string& s, int k){if(board[i][j] != s[k]) return false;if(k == s.size() - 1) return true;visited[i][j] = 1;bool ans = false;for(auto dir : dirs){int cur_i = i + dir.first, cur_j = j + dir.second;if(cur_i >= 0 && cur_i < m && cur_j >= 0 && cur_j < n && visited[cur_i][cur_j] == 0) {if(check(board, visited, cur_i, cur_j, s, k + 1)){ans = true;break;}}}visited[i][j] = 0;return ans;}
public:bool exist(vector<vector<char>>& board, string word) {m = board.size(); n = board[0].size(); vector<vector<int>> visited(m, vector<int>(n));for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(check(board, visited, i, j, word, 0))return true;}}return false;}
};
Java
class Solution {private int[][] dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};private int m, n;private boolean check(char[][] board, int[][] visited, int i, int j, String s, int k){if(board[i][j] != s.charAt(k)) return false;if(k == s.length() - 1) return true;visited[i][j] = 1;boolean ans = false;for(int[] dir : dirs){int cur_i = i + dir[0], cur_j = j + dir[1];if(cur_i >= 0 && cur_i < m && cur_j >= 0 && cur_j < n && visited[cur_i][cur_j] == 0) {if(check(board, visited, cur_i, cur_j, s, k + 1)){ans = true;break;}}}visited[i][j] = 0;return ans;}public boolean exist(char[][] board, String word) {m = board.length; n = board[0].length; int[][] visited = new int[m][n];for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){if(check(board, visited, i, j, word, 0))return true;}}return false;}
}
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度:一个非常宽松的上界为 O ( m n ∗ 3 l ) O(mn*3^l) O(mn∗3l),其中
m,n为网格的长度与宽度,l为字符串word的长度。在每次调用函数check时,除了第一次可以进入 4 个分支以外,其余时间我们最多会进入 3 个分支(因为每个位置只能使用一次,所以走过来的分支没法走回去)。 - 空间复杂度: O ( m n ) O(mn) O(mn)。我们额外开辟了 O ( m n ) O(mn) O(mn) 的
visited数组,同时栈的深度最大为 O ( m i n ( l , m n ) ) O(min(l, mn)) O(min(l,mn))。。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!
注: 如有不足,欢迎指正!
相关文章:

(搜索) 剑指 Offer 12. 矩阵中的路径 ——【Leetcode每日一题】
❓剑指 Offer 12. 矩阵中的路径 难度:中等 给定一个 m * n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构…...
构建高可用的去中心化微服务集群架构指南
随着云计算、大数据和物联网的快速发展,企业对于可扩展的、高性能的微服务架构的需求也日益增长。传统的集中式架构已经不能满足这些需求,因此出现了去中心化的微服务集群架构。本文将介绍如何构建高可用的去中心化微服务集群架构,以满足企业…...

Sui主网升级至V1.7.1版本
Sui主网现已升级至V1.7.1版本,此升级包含了多项修复和优化。升级要点如下所示: #12915 协议版本提升至20版本。 在Sui框架中新增Kiosk Extensions API和一个新的sui::kiosk_extension模块。 您可以使用该API构建自定义的Kiosk应用程序,以…...
-[基础知识])
自然语言处理从入门到应用——LangChain:索引(Indexes)-[基础知识]
分类目录:《自然语言处理从入门到应用》总目录 索引(Indexes)是指为了使LLM与文档更好地进行交互而对其进行结构化的方式。在链中,索引最常用于“检索”步骤中,该步骤指的是根据用户的查询返回最相关的文档:…...
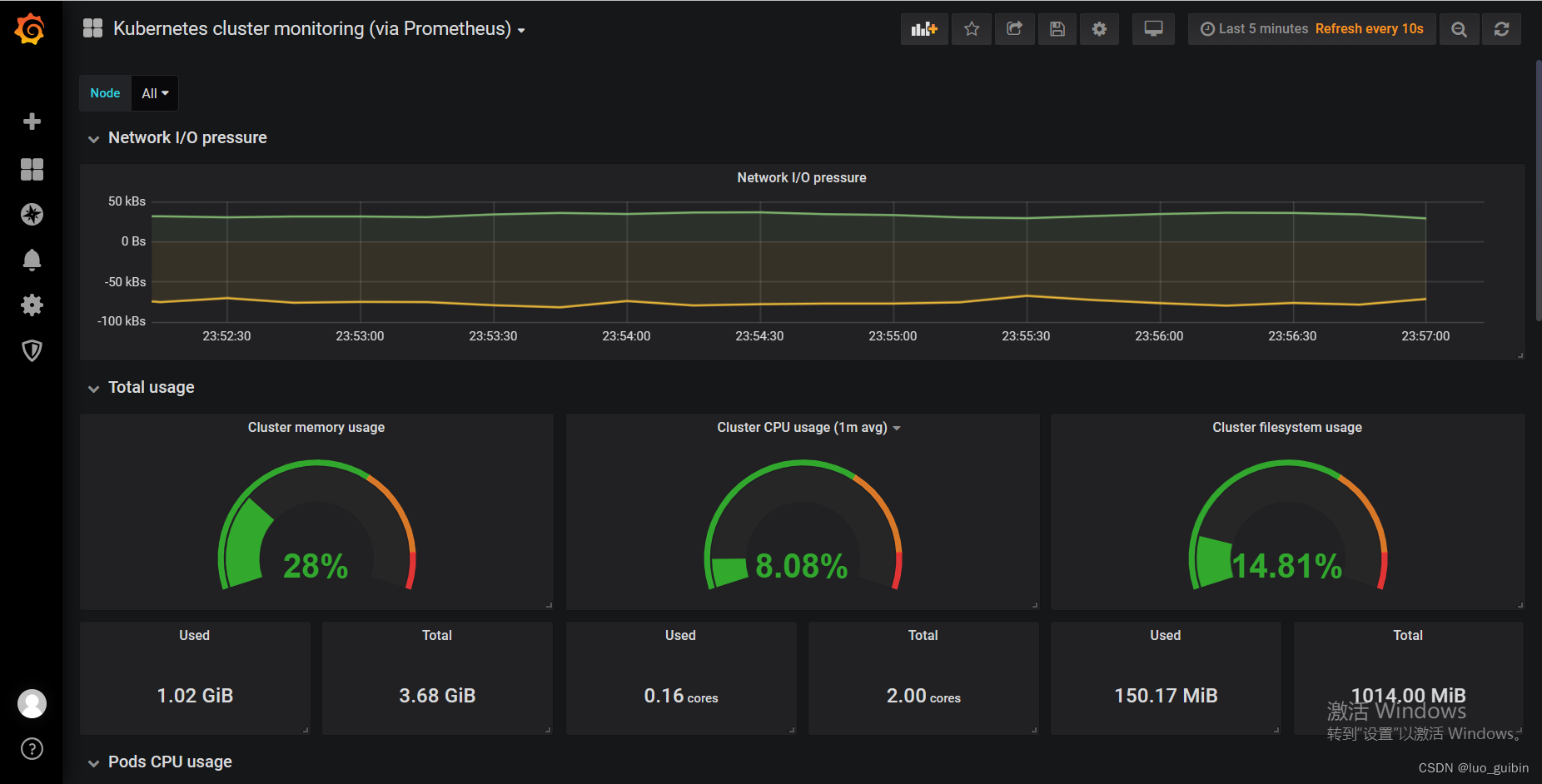
k8s集群监控方案--node-exporter+prometheus+grafana
目录 前置条件 一、下载yaml文件 二、部署yaml各个组件 2.1 node-exporter.yaml 2.2 Prometheus 2.3 grafana 2.4访问测试 三、grafana初始化 3.1加载数据源 3.2导入模板 四、helm方式部署 前置条件 安装好k8s集群(几个节点都可以,本人为了方便实验k8s集…...
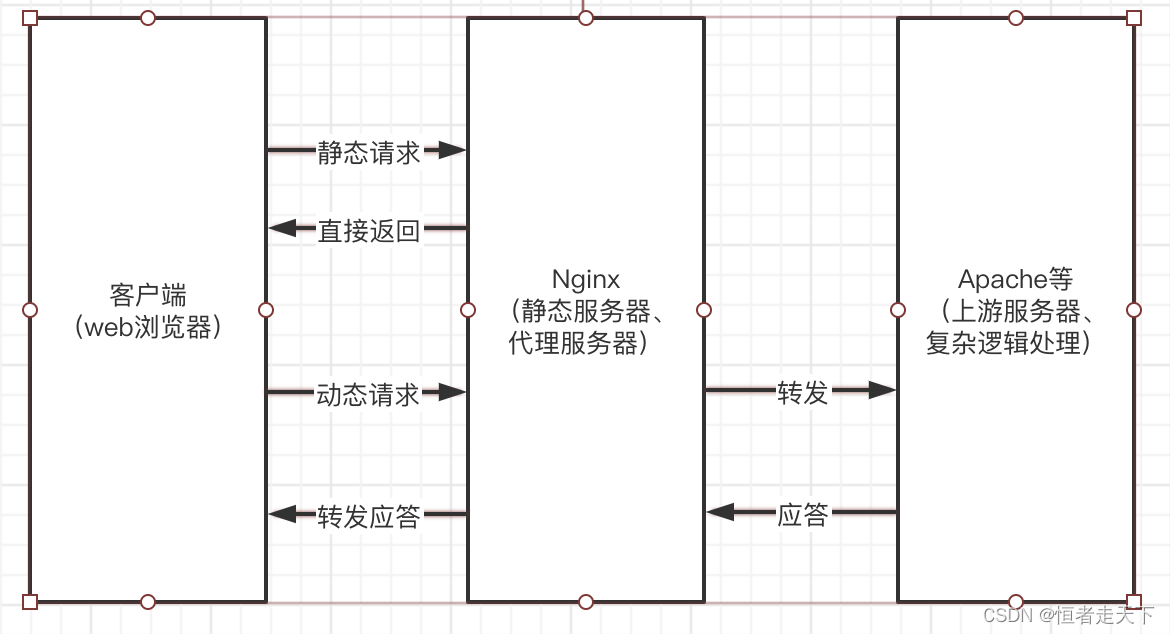
nginx反向代理流程
一、nginx反向代理流程 反向代理:使用代理服务器来接受internet上的连接请求,然后将请求转发给内部网络中的上游服务器,并将上游服务器得到的结果返回给请求连接的客户端,代理服务器对外表现就是一个web服务器。Nginx就经常拿来做…...

Java“牵手”根据店铺ID获取淘宝店铺所有商品数据方法,淘宝API实现批量店铺商品数据抓取示例
淘宝天猫商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取淘宝整店所有商品详情页面评价内容数据,您可以通过开放平台的接口或者直接访问淘宝商城的网页来获取店铺所有商品详情信息内的评论数据…...

从0开始yolov8模型目标检测训练
从0开始yolov8模型目标检测训练 1 大环境 首先有大环境,即已经准备好了python、nvidia驱动、cuda、cudnn等。 2 yolov8的虚拟环境 2.1 创建虚拟环境 conda create -n yolov8 python3.102.2 激活虚拟环境 注意:激活虚拟环境的时候,需要清…...

设计模式-抽象工厂模式
抽象工厂模式:该模式是对工厂模式的拓展,因为工厂模式中创建的产品都需要继承自同一个父类或接口,创建的产品类型相同,无法创建其他类型产品,所以抽象工厂模式对其进行拓展,使其可以创建其他类型的产品。 …...
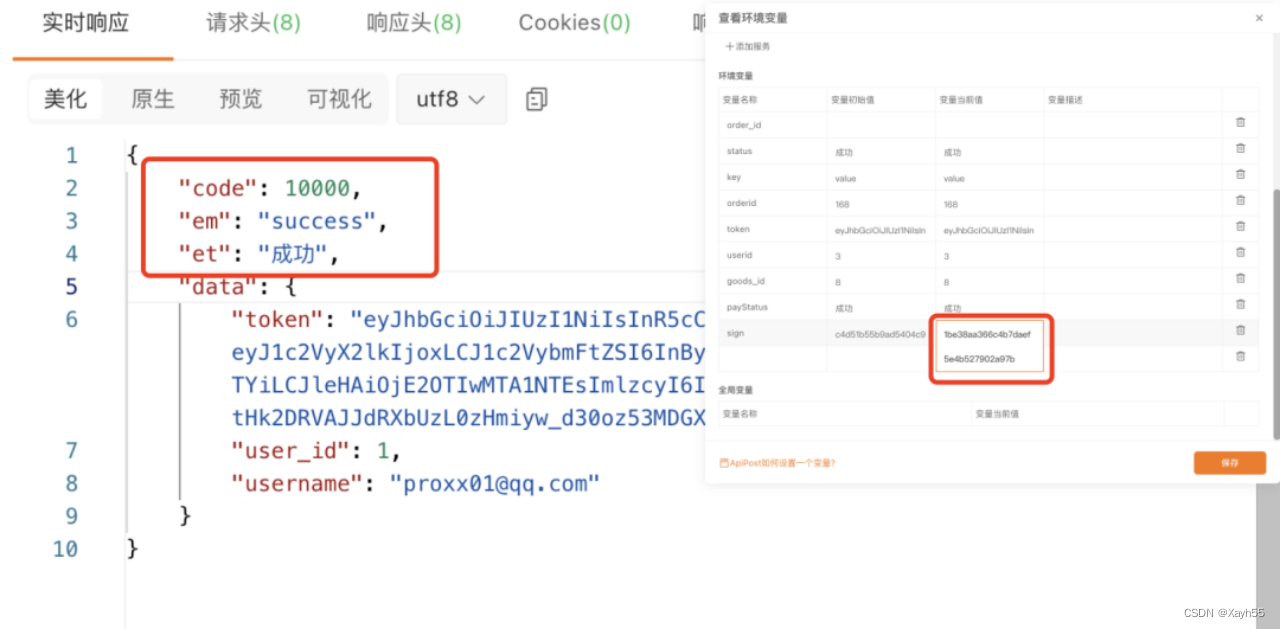
如何用Apipost实现sign签名?
我们平常对外的接口都会用到sign签名,对不同的用户提供不同的apikey ,这样可以提高接口请求的安全性,避免被人抓包后乱请求。 如何用Apipost实现sign签名? 可以在Apipost中通过预执行脚本调用内置的JS库去实现预执行脚本是在发送请求之前自…...
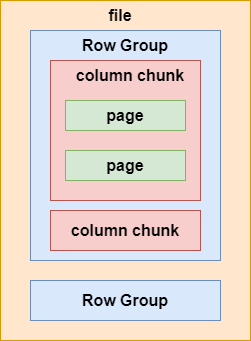
Hive底层数据存储格式
前言 在大数据领域,Hive是一种常用的数据仓库工具,用于管理和处理大规模数据集。Hive底层支持多种数据存储格式,这些格式对于数据存储、查询性能和压缩效率等方面有不同的优缺点。本文将介绍Hive底层的三种主要数据存储格式:文本文件格式、Parquet格式和ORC格式。 一、三…...
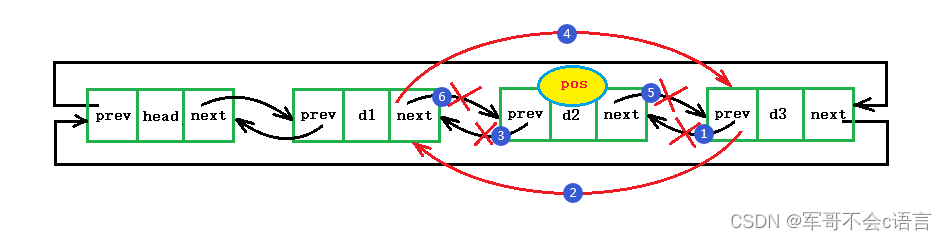
双向-->带头-->循环链表
目录 一、双向带头循环链表概述 1.什么是双向带头循环链表 2.双向带头循环链表的优势 3.双向带头循环链表简图 二、双向带头循环链表的增删查改图解及代码实现 1.双向带头循环链表的头插 2.双向带头循环链表的尾插 3.双向带头循环链表的头删 4.双向带头循环链表的尾删…...

Opencv4基于C++基础入门笔记:OpenCV环境配置搭建
文章目录: 一:软件安装 二:配置环境(配置完之后重启一下软件) 1.配置电脑系统环境变量 vs2012及其以下 vs2014及其以上 2.配置VS软件环境变量 vs2012及其以下 vs2014及其以上 三:测试 vs2012及其…...

JS基础之实现map方法
提示:内容虽少,但是里面也有好几个知识点。 step 1:实现函数 function mapTmp (fn){if(!Array.isArray(this) || !this?.length) return [];const arr [];this.forEach((item, index) > {const newItem fn(item, index, this);arr.pu…...
FPGA应用学习笔记-----复位电路(二)和小结
不可复位触发器若和可复位触发器混合写的话,不可复位触发器是由可复位触发器馈电的。 不应该出现的复位,因为延时导致了冒险,异步复位存在静态冒险 附加素隐含项,利用数电方法,消除静态冒险 这样多时钟区域还是算异步的…...
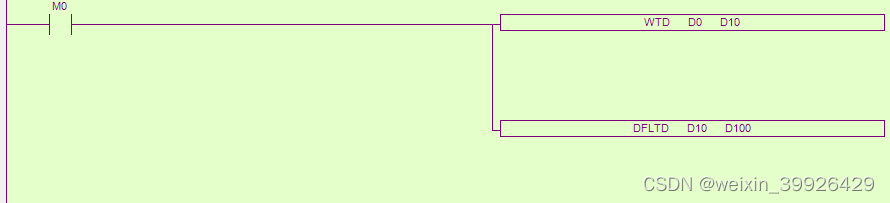
信捷 XD PLC 16位整数转换为双精度浮点数
完成16位整数转换为双精度浮点数,信捷XD PLC需要两个指令,逐步转换,一个指令搞不定。 具体的: 第1步:int16->int32 第2步:int32->Double 例子,比如说将D0转换成浮点数放到D100~D103...
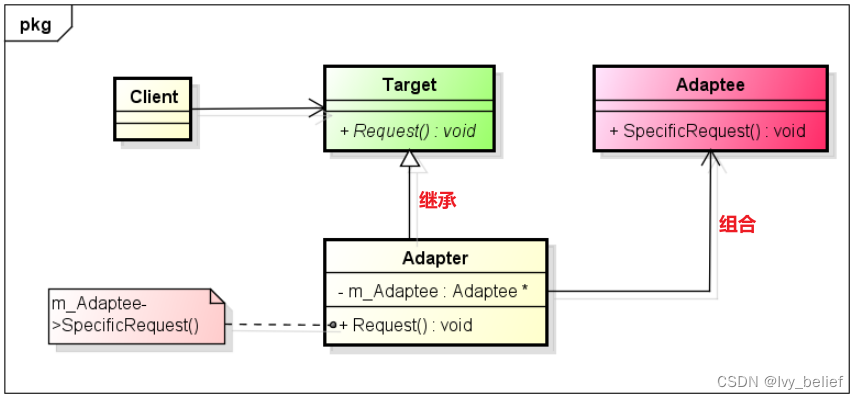
(二)结构型模式:1、适配器模式(Adapter Pattern)(C++实现示例)
目录 1、适配器模式(Adapter Pattern)含义 2、适配器模式应用场景 3、适配器模式的UML图学习 4、C实现适配器模式的示例 1、适配器模式(Adapter Pattern)含义 将一个接口转换为客户端所期待的接口,从而使两个接口…...
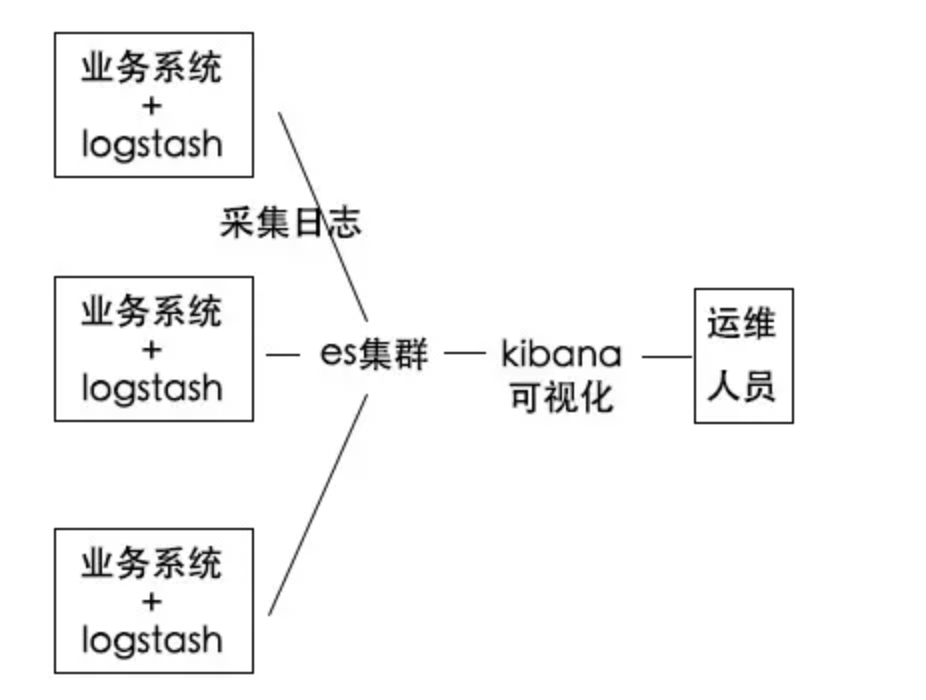
【编程二三事】ES究竟是个啥?
在最近的项目中,总是或多或少接触到了搜索的能力。而在这些项目之中,或多或少都离不开一个中间件 - ElasticSearch。 今天忙里偷闲,就来好好了解下这个中间件是用来干什么的。 ES是什么? ES全称ElasticSearch,是个基于Lucen…...
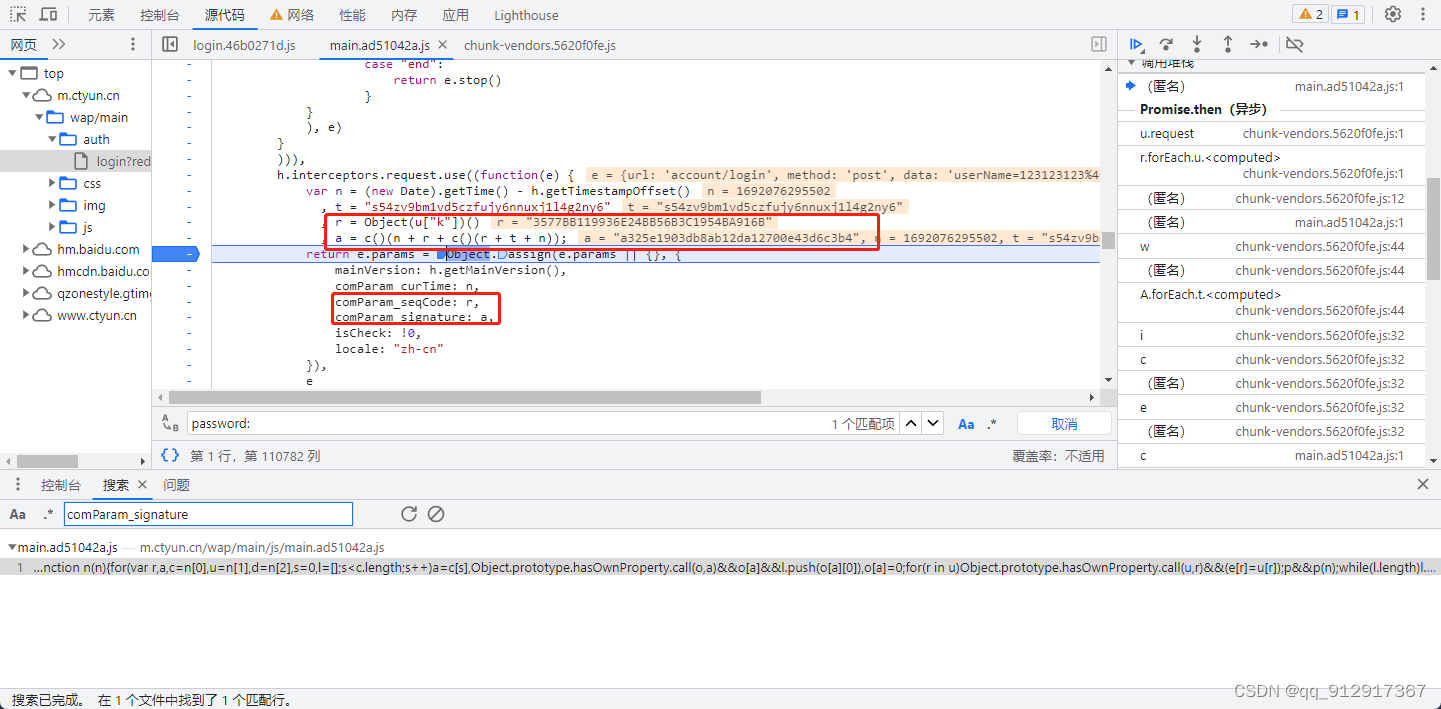
爬虫逆向实战(三)--天某云登录
一、数据接口分析 主页地址:天某云 1、抓包 通过抓包可以发现登录接口是account/login 2、判断是否有加密参数 请求参数是否加密? 通过“载荷”模块可以发现password、comParam_signature、comParam_seqCode是加密的 请求头是否加密? 无…...

不要过于迷恋软件架构,要重视如何设计根据简单和清晰的设计
1. 设计一个计算机系统的目标应该是简单性 。 系统越简单,理解起来就越简单,找到问题就越简单,实现它就越简单。描述的语言越清晰,设计就越容易理解。 干净的设计类似于干净的代码:它易于阅读且易于理解。 2. 如何编…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
