Go 1.21新增的内置函数(built-in functions)详解
Go 1.21新增的内置函数分别是 min、max 和 clear,接下来看下这几个函数的用途和使用示例。
在编程过程中,需要知道一组值中的最大或最小值的场景是很常见的,比如排序、统计等场景。之前都需要自己写代码来实现这个功能,现在 Go 1.21引入了两个新的内置函数 min 和 max 来实现了这个功能。
min
函数定义如下:
func min[T cmp.Ordered](x T, y ...T) T用于计算给定数量的有序类型数据中的的最小值,参数至少为一个。与操作符相同的类型规则适用:对于有序参数 x 和 y,如果 x + y 有效,则 min(x, y) 有效,并且 min(x, y) 的类型和 x + y 的类型也一样(对于 max 函数也是类似的)。如果所有参数都是常量,则结果也是常量。简单示例如下:
package mainimport "fmt"func main() {var x, y int = 1, 6fmt.Println(min(y)) // 6fmt.Println(min(x, y)) // 1fmt.Println(min(0, x, y)) // 0fmt.Println(min(x, y, 4.0)) // 1fmt.Println(min("a", "b")) // a
}max
函数定义如下:
func max[T cmp.Ordered](x T, y ...T) T用于计算给定数量的有序类型数据中的的最大值,参数至少为一个,其他特性和 min 类似。简单示例如下:
package mainimport "fmt"func main() {var x, y int = 1, 6fmt.Println(max(y)) // 6fmt.Println(max(x, y)) // 6fmt.Println(max(0, x, y)) // 6fmt.Println(max(x, y, 4.0)) // 6fmt.Println(max("a", "b")) // b
}Clear
函数定义如下:
func clear[T ~[]Type | ~map[Type]Type1](t T)作用是删除或清空所有元素。接受 map 和 slice类型的实参。当参数为 map 类型时,会删除 map 中所有元素,map 的长度变为 0,简单示例如下:
package mainimport "fmt"func main() {m := map[string]string{"foo": "bar", "foo2": "bar2"}clear(m)fmt.Println(len(m)) // 0
}当参数为切片类型时,将切片中的所有元素设置为对应类型的零值,clear 前后切片的长度和容量都保持不变。
package mainimport "fmt"func main() {s1 := []int{1, 2, 3, 4}clear(s1)fmt.Println(s1) // [0 0 0 0]s2 := []string{"路多辛的博客", "路多辛的所思所想", "a", "b"}clear(s2)fmt.Println(s2) // [ ]
}如果传入的 map 或 slice 类型值为 nil,则不做任何操作。
相关文章:
详解)
Go 1.21新增的内置函数(built-in functions)详解
Go 1.21新增的内置函数分别是 min、max 和 clear,接下来看下这几个函数的用途和使用示例。 在编程过程中,需要知道一组值中的最大或最小值的场景是很常见的,比如排序、统计等场景。之前都需要自己写代码来实现这个功能,现在 Go 1…...
【云原生,k8s】基于Helm管理Kubernetes应用
第四阶段 时 间:2023年8月18日 参加人:全班人员 内 容: 基于Helm管理Kubernetes应用 目录 一、Kubernetes部署方式 (一)minikube (二)二进制包 (三)Kubeadm …...

字符设备驱动分布注册
驱动文件: 脑图: 现象:...
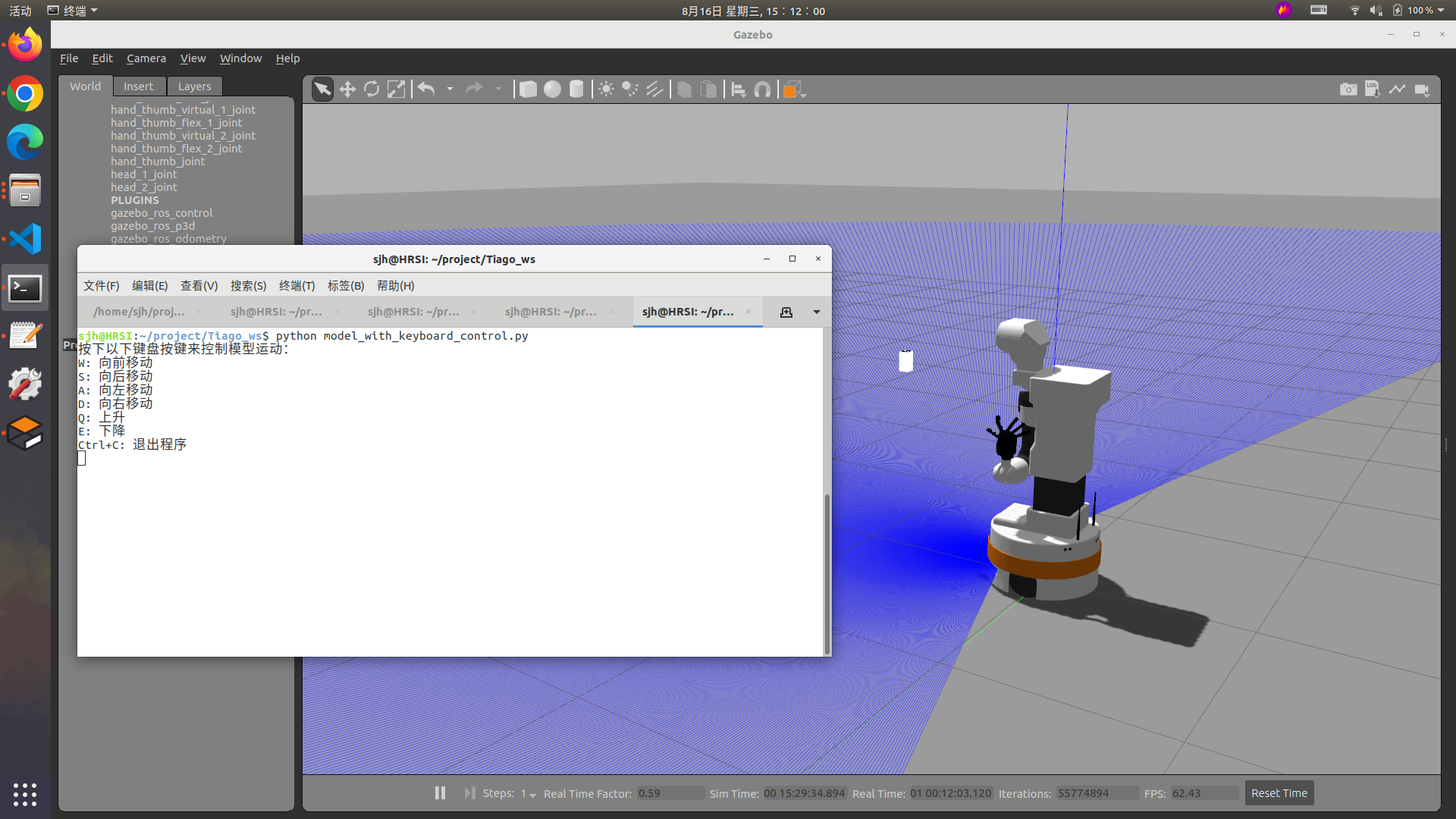
在Gazebo中添加悬浮模型后,利用键盘控制其移动方法
前段时间写了文章,通过修改sdf、urdf模型的方法,在Gazebo中添加悬浮模型方法 / Gazebo中模型如何不因重力下落:在Gazebo中添加悬浮模型方法 / Gazebo中模型如何不因重力下落:修改sdf、urdf模型_sagima_sdu的博客-CSDN博客 今天讲…...
 模板方法设计模式)
Java设计模式 (一) 模板方法设计模式
什么是模板方法设计模式? 模板方法设计模式是一种行为型设计模式,它定义了一个算法的骨架,并将一些步骤的具体实现延迟到子类中。模板方法模式可以帮助确保在算法的不同部分中保持一致性,同时也允许子类根据需要进行具体实现。 模板方法模式…...

PHP在线客服系统推荐
在当今数字化时代,企业客户服务的重要性不容忽视。为了提供卓越的客户体验,许多企业正在寻找PHP在线客服系统。这种系统不仅可以满足客户的需求,还能提升企业的形象。本文将深入探讨PHP在线客服系统的一些有趣话题。 理解PHP在线客服系统 PHP…...
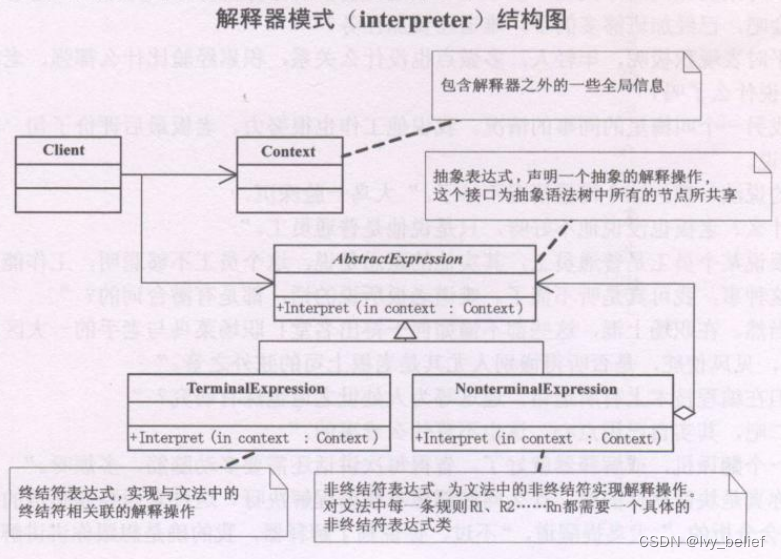
(三)行为型模式:3、解释器模式(Interpreter Pattern)(C++示例)
目录 1、解释器模式(Interpreter Pattern)含义 2、解释器模式的UML图学习 3、解释器模式的应用场景 4、解释器模式的优缺点 5、C实现解释器模式的实例 1、解释器模式(Interpreter Pattern)含义 解释器模式(Interp…...

Zookeeper 启动闪退
常见的大概这两种情况 1.找不到zoo.cfg文件 在下载zookeeper后,在 %zookeeper安装目录%/conf 目录下有一个zoo.sample.cfg 文件,把 zoo.sample.cfg 文件改名为 zoo.cfg 再重启zkServer.cmd echo off REM Licensed to the Apache Software Foundation …...
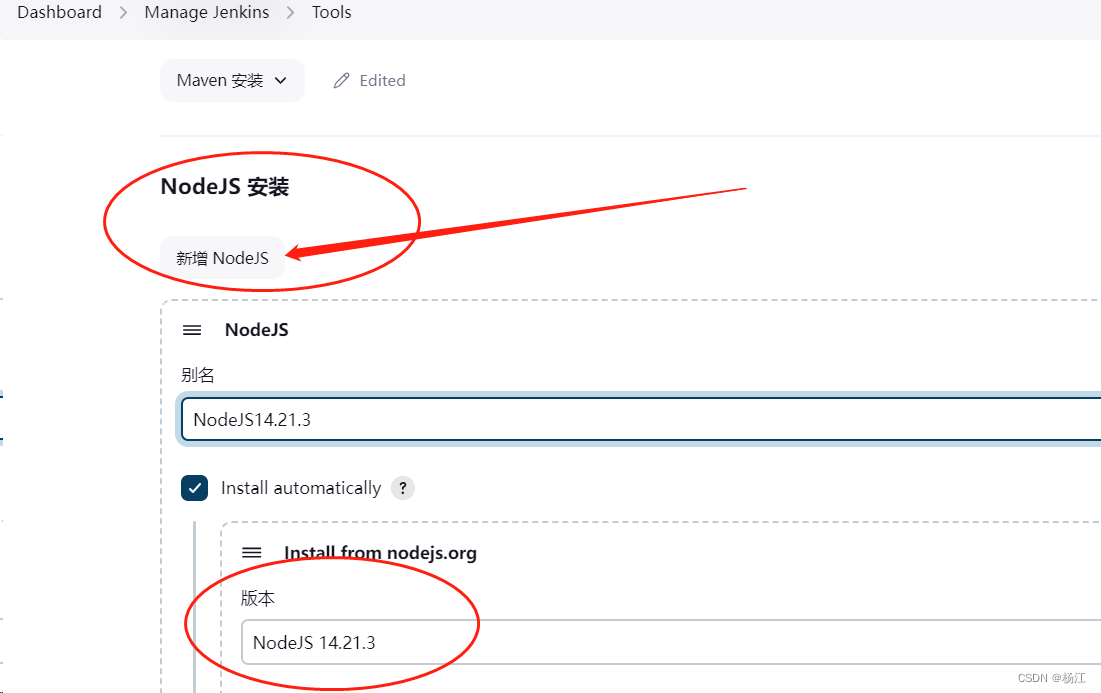
jenkins 安装nodejs 14
参考: jenkins容器安装nodejs-前端问答-PHP中文网...
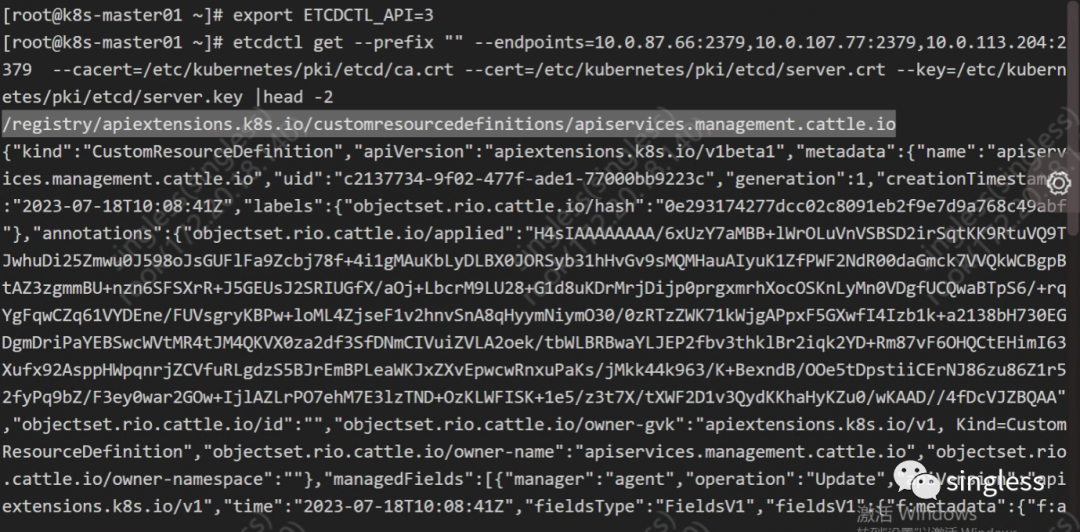
K8S核心组件etcd详解(上)
1 介绍 https://etcd.io/docs/v3.5/ etcd是一个高可用的分布式键值存储系统,是CoreOS(现在隶属于Red Hat)公司开发的一个开源项目。它提供了一个简单的接口来存储和检索键值对数据,并使用Raft协议实现了分布式一致性。etcd广泛应用…...
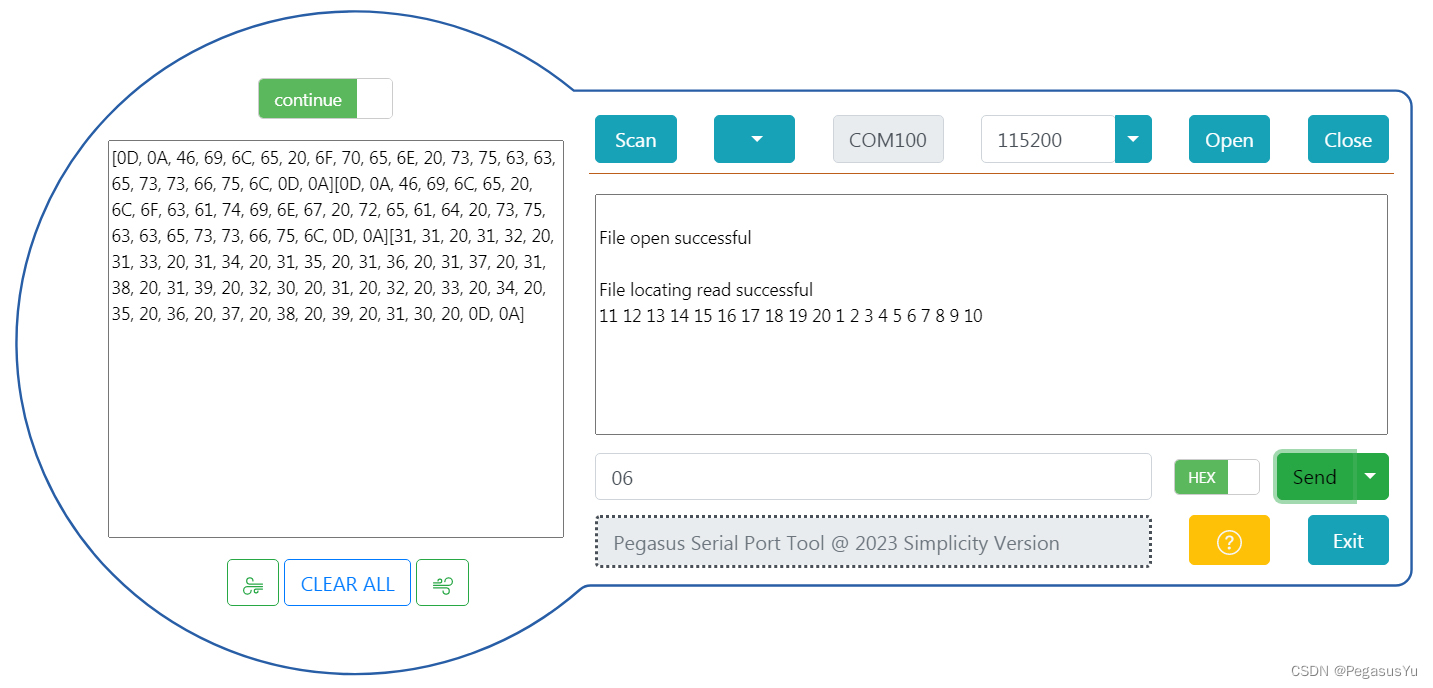
STM32存储左右互搏 I2C总线FATS读写EEPROM ZD24C1MA
STM32存储左右互搏 I2C总线FATS读写EEPROM ZD24C1MA 在较低容量存储领域,EEPROM是常用的存储介质,可以通过直接或者文件操作方式进行读写。不同容量的EEPROM的地址对应位数不同,在发送字节的格式上有所区别。EEPROM是非快速访问存储…...
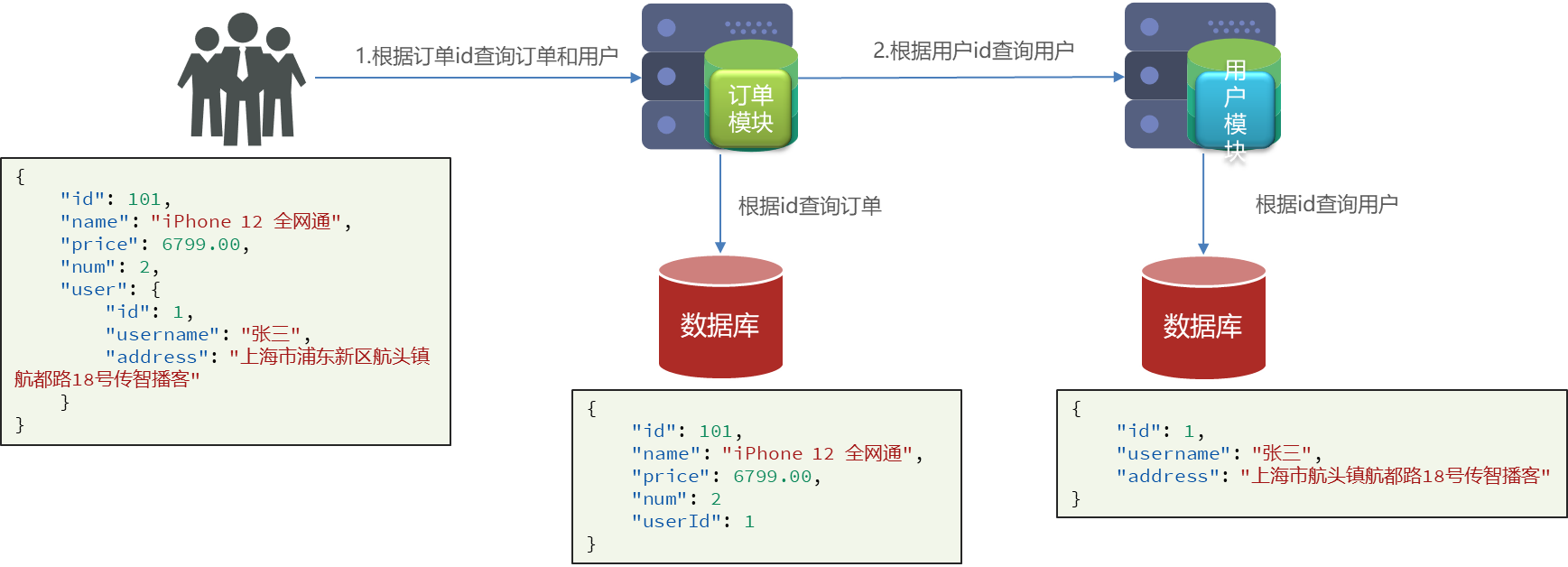
微服务—远程调用(RestTemplate)
在微服务的所有框架中,SpringCloud脱颖而出,它是目前国内使用的最广泛的微服务框架 (官网地址),它集成了各种微服务功能组件,并基于SpringBoot实现了这些组件的自动装配,从而提供了良好的开箱…...
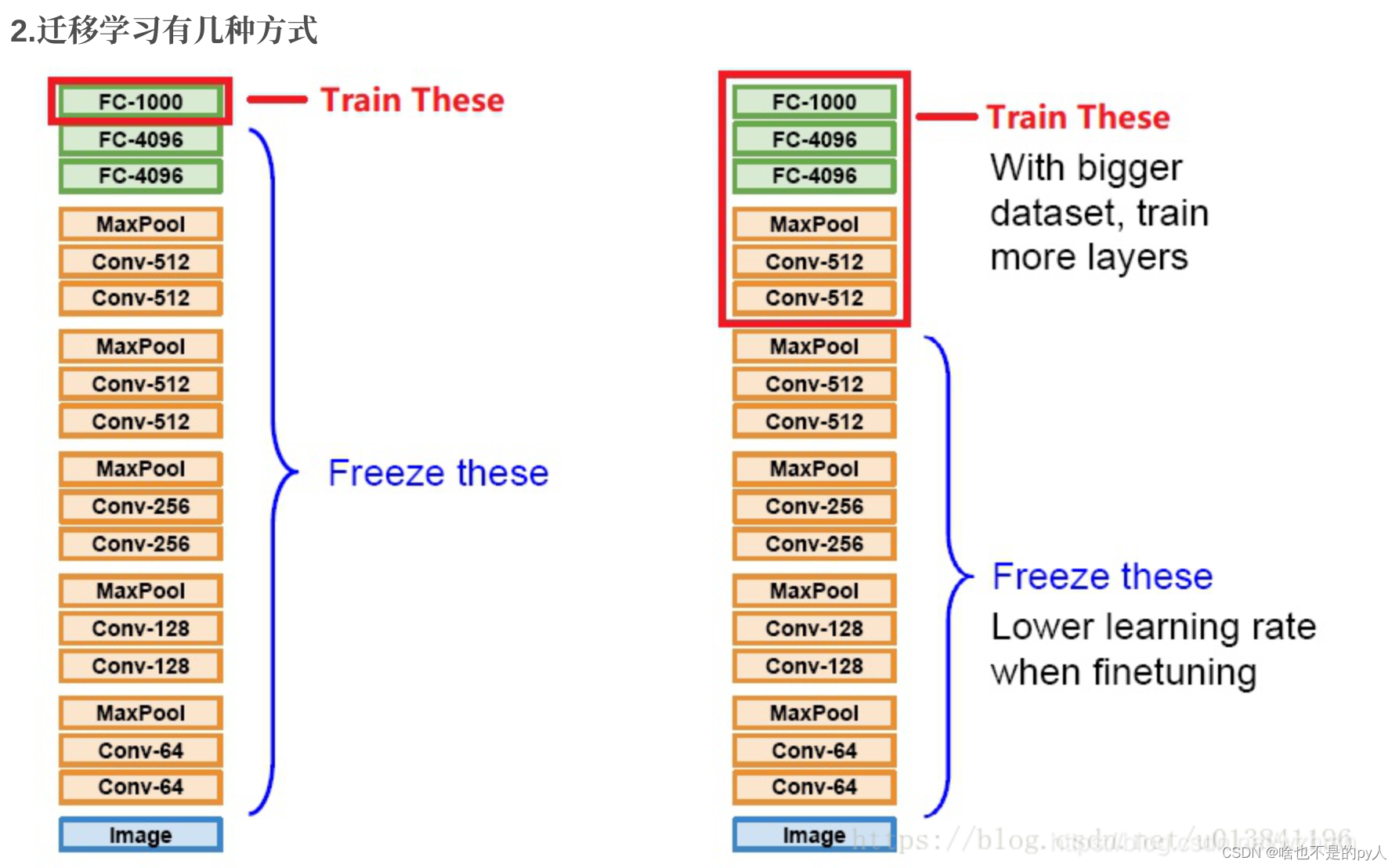
Fine tune简介
目录 Intro Related work Example .1 重新训练 .2 使用新的数据集进行fine tune .3 修改net结构 References 移学习不是一种算法而是一种机器学习思想,应用到深度学习就是微调(Fine-tune)。通过修改预训练网络模型结构(如修改样本类别输出个数),选择性载入预训练网络…...

centos nginx配置ipv4和ipv6的地址都可以访问同一个网站
标题centos nginx配置ipv4和ipv6的地址都可以访问同一个网站 在 Nginx 中配置使 IPv4 和 IPv6 地址都可以访问同一个网站相对简单。只需要确保 Nginx 配置文件正确地配置了监听 IPv4 和 IPv6 地址的监听器即可。 打开你的 Nginx 配置文件,通常位于 /etc/nginx/nginx…...

高教杯数学建模2020C题总结
🧡1. 前言🧡 跟队友花了三天模拟2020C题,现在整理一下一些数据处理的代码,以及在模拟中没有解决的问题。方便以后回溯笔记。 🧡2. 数据处理🧡 2.1 导入数据,并做相关预处理 import pandas a…...

Swagger
目录 简介 使用方式: 常用注解 简介 使用Swagger你只需要按照他的规范去定义接口及接口相关信息再通过Swagger衍生出来的一系列项目和工具,就可以做到生成各种格式的接口文档,以及在线接口调试页面等等。 官网:https://swagger…...

Android 13像Settings一样获取热点和网络共享
一.背景 由于客户定制的Settings里面需要获取到热点和网络共享状态,所以需要实现此功能。 目录 一.背景 二.前提条件 三.调用api 二.前提条件 首先应用肯定要是系统应用,并且导入framework.jar包,具体可以参考: Android 应用自动开启辅助(无障碍)功能并使用辅助(无障碍…...
操作系统搭建相关知识
文章目录 系统篇netstat命令systemctl命令Systemd系统资源分类(12类) 网络篇ifconfig命令操作系统配置动态IP脚本dhcp服务的安装与配置防火墙相关知识 操作系统常用配置文件 系统篇 netstat命令 netstat指路 systemctl命令 常用于重启系统的每个服务…...

【校招VIP】前端校招考点之vue底层特性
考点介绍: 大家在面试途中遇到的相对多的问题,也是难点的问题,一般都有vue底层原理。对于只会用但是不懂的小白来说真是太痛苦了,仅仅能说出来 一些 数据劫持,双向数据绑定,虚拟dom树的名词来说远远不够。 …...
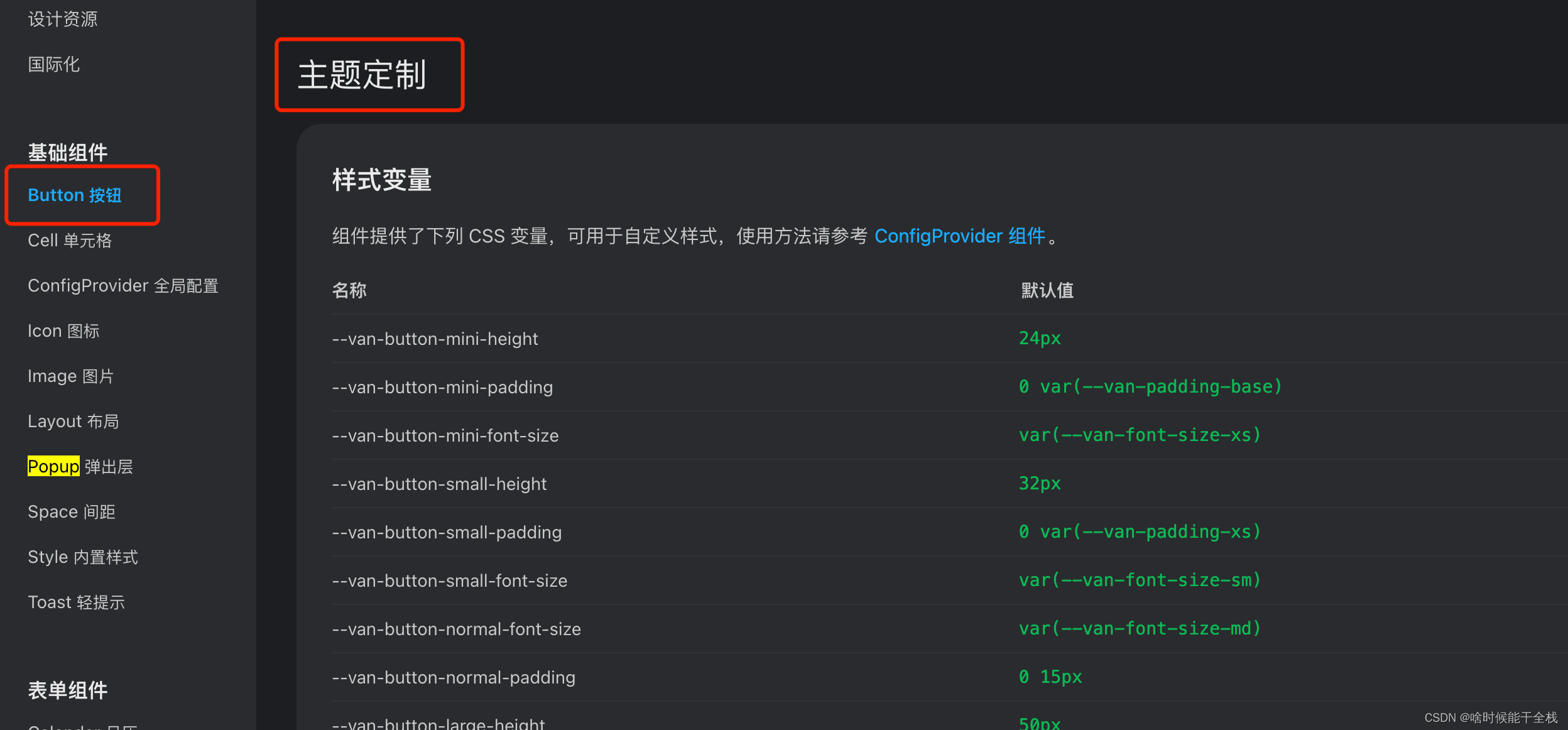
vue3+vite配置vantUI主题
❓在项目中统一配置UI主题色,各个组件配色统一修改 vantUI按需安装 参考vantUI文档 创建vantVar.less文件夹进行样式编写 vantVar.less :root:root{//导航--van-nav-bar-height: 44px;//按钮--van-button-primary-color: #ffffff;--van-button-primary-backgr…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
