leetcode240+Search a 2D Matrix II+从右上角开始
链接
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {if(matrix.size()==0 || matrix[0].size()==0) return false;int i=0, j=matrix[0].size()-1; //从右上角开始while (i<matrix.size()&&j>=0) {int x = matrix[i][j];if(target==x) return true;else if(target<x){ //必须先纵轴j-=1;}else if(target>x){i+=1;}}return false;}
};
相关文章:

leetcode240+Search a 2D Matrix II+从右上角开始
链接 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {if(matrix.size()0 || matrix[0].size()0) return false;int i0, jmatrix[0].size()-1; //从右上角开始while (i<matrix.size()&&j>0) {int x mat…...
0xL4ugh 2023
这回跟着个队伍跑,不过还是2X以后的成绩,前边太卷了。自己会的部分,有些是别人已经提交了的。记录一下。Cryptocrypto 1给了一些数据,像这样就没有别的了ct [0, 1, 1, 2, 5, 10, 20, 40, 79, 159, 317, 635, 1269, 2538, 5077, 1…...

Mybatis(4)之跟着老杜做一个简单的银行转账会话
这是个MVC项目,我不一定可以完整的实现这个项目,但力求把这个复现出来,尽量的复现细节。 第一步:创建数据库 表 创建表如下: 我们使用 int 是为了方便 然后采用 demcial,精确度较高 添加两个用户 然后…...

VBA提高篇_ 22 事件处理
文章目录1.事件编程2.常用工作簿事件名称与对应处理过程名称示例3. 事件编程的步骤4.工作簿事件4.1 Open4.2 BeforeClose4.3 NewSheet5.工作表事件6.变量和过程函数的作用域1.事件编程 写在事件发生地(对应工作簿或工作表) 2.常用工作簿事…...

【蓝桥杯集训·周赛】AcWing 第91场周赛
文章目录第一题 AcWing 4861. 构造数列一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第二题 AcWing 4862. 浇花一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解第三题 AcWing 4861. 构造数列一、题目1、原题…...
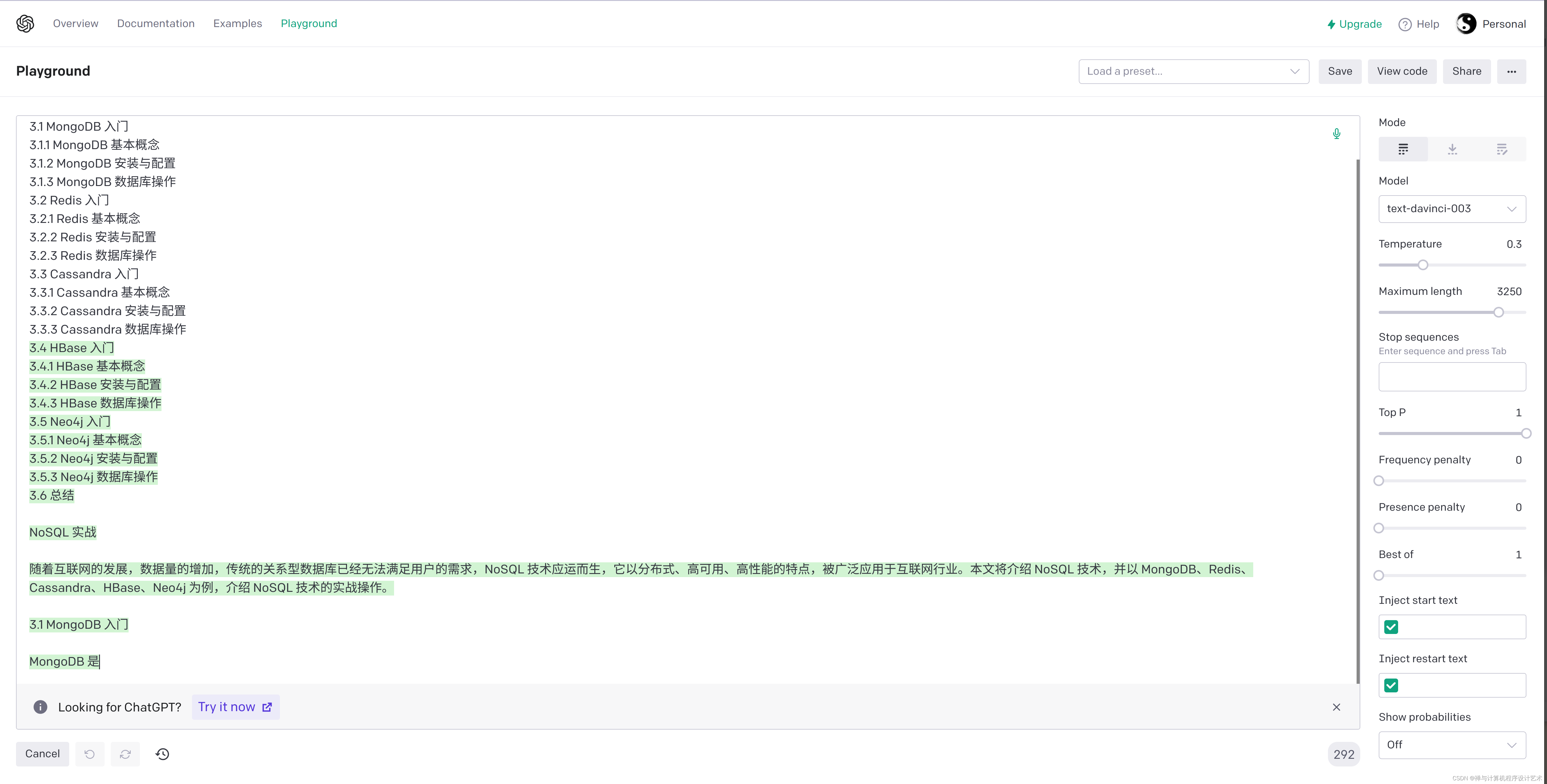
【人工智能AI】三、NoSQL 实战《NoSQL 企业级基础入门与进阶实战》
帮我写一篇介绍NoSQL的技术文章,文章标题是《NoSQL 实战》,不少于3000字。这篇文章的目录是 3.NoSQL 实战 3.1 MongoDB 入门 3.1.1 MongoDB 基本概念 3.1.2 MongoDB 安装与配置 3.1.3 MongoDB 数据库操作 3.2 Redis 入门 3.2.1 Redis 基本概念 3.2.2 Red…...
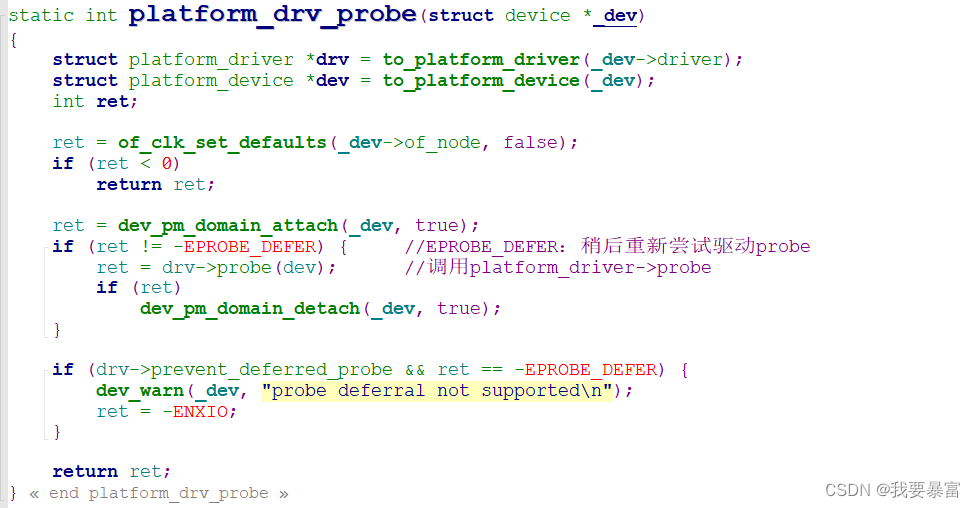
platform 总线
驱动的分离与分层思想 分离:硬件信息分离; 在编写硬件驱动的时候,需要操作许多硬件寄存器。比如gpio 驱动,你需要知道gpio控制器 寄存器的地址,你想要哪个gpio输出?或是输入? 这些操作最终都是靠设置寄存…...

2023第10届生物发酵展3月30-4月1号山东济南开展,参观路线来了
2023第10届生物发酵展3月30-4月1号山东济南开展,参观路线来了!展会时间:2023年3月30日-4月1日展馆地址:山东国际会展中心(济南市槐荫区日照路1号)展馆:4号馆、5号馆BIO CHINA生物发酵展…...

RK356x U-Boot研究所(命令篇)3.6 fdt命令的用法
平台U-Boot 版本Linux SDK 版本RK356x2017.09v1.2.3文章目录 一、fdt命令的配置二、fdt命令的定义三、fdt命令的用法3.1 fdt list3.2 fdt rm3.3 fdt set一、fdt命令的配置 .config配置文件需要有以下配置: rk3568_defconfig默认已使能。 二、fdt命令的定义 usb命令定义在cm…...

2023年社工工资多少钱一月 能领多少补贴
2023年社会工作者人员的待遇还算可以,每月的全额工资一共5000多,扣完五险一金以后每月的到手工资一共4000多,不同地区薪资也是不同的,一线城市会在7千元以上,还可以领取几百到几千元不等的补贴。 12023年社工工资多少钱…...
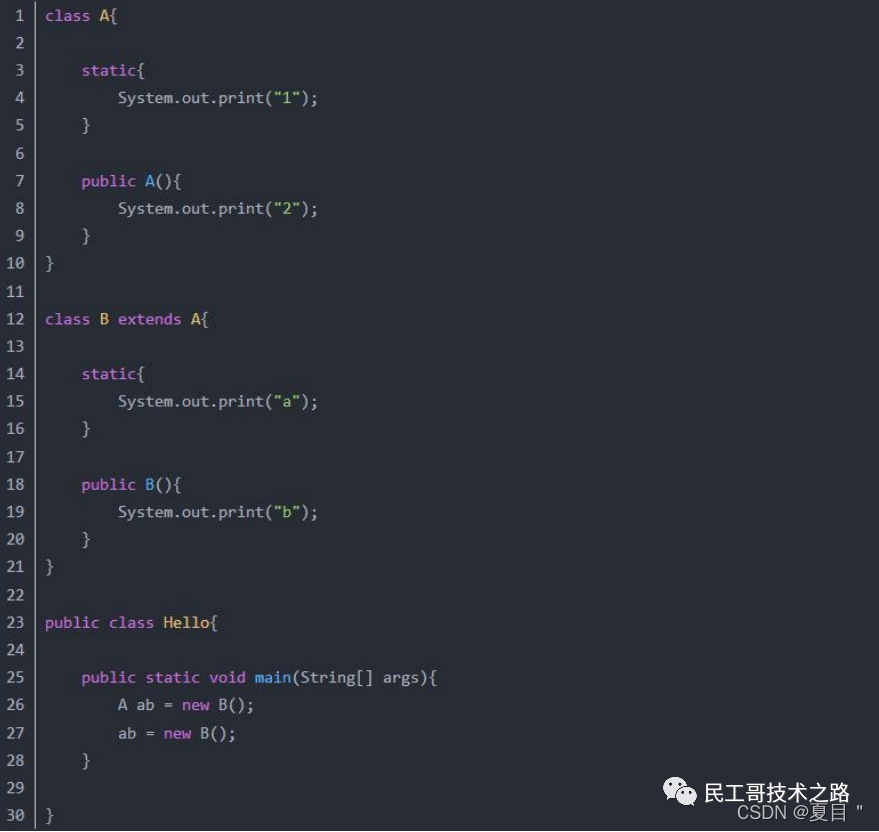
面试攻略,Java 基础面试 100 问(十一)
抽象类(abstract class)和接口(interface)有什么异同? 抽象类和接口都不能够实例化,但可以定义抽象类和接口类型的引用。一个类如果继承了某个抽象类或者实现了某个接口都需要对其中的抽象方法全部进行实现ÿ…...

接口测试(Fiddler工具)
目录 1.Fiddler是什么? 2.Fiddler的原理 3.Fiddler安装 4.Fiddler界面 4.1.常用工具 4.2 会话列表 4.3 状态栏 4.4 内容显示区 1.Fiddler是什么? Fiddler是客户端与服务器之间的HTTP代理,是当前最常用的HTTP协议抓包工具。 主要功能&a…...

Debian/Ubuntu 安装和使用 perf 调试工具
为操作系统安装基本依赖环境:apt-get update -y apt-get upgrade -y apt-get install lrzsz zip unzip libkrb5-dev libicu-dev screen iftop openssl libssl-dev libunwind8 iftop net-tools gcc gdb cmake curl wget -y apt-get install gcc gdb cmake python-dev…...

【Python语言基础】——Python NumPy 数组连接
Python语言基础——Python NumPy 数组连接 文章目录 Python语言基础——Python NumPy 数组连接一、Python NumPy 数组连接一、Python NumPy 数组连接 连接 NumPy 数组 连接意味着将两个或多个数组的内容放在单个数组中。 在 SQL 中,我们基于键来连接表,而在 NumPy 中,我们按…...
解决IDEA报错:无效的目标发行版: 17
解决IDEA报错:无效的目标发行版: 17 目录解决IDEA报错:无效的目标发行版: 17报错由来解决报错【1】检查setting设置,查看编译器编译模块的编译版本是否是你需要的【2】尝试去修改当前项目的启动设置,设置JRE为你需要的版本。【3】…...
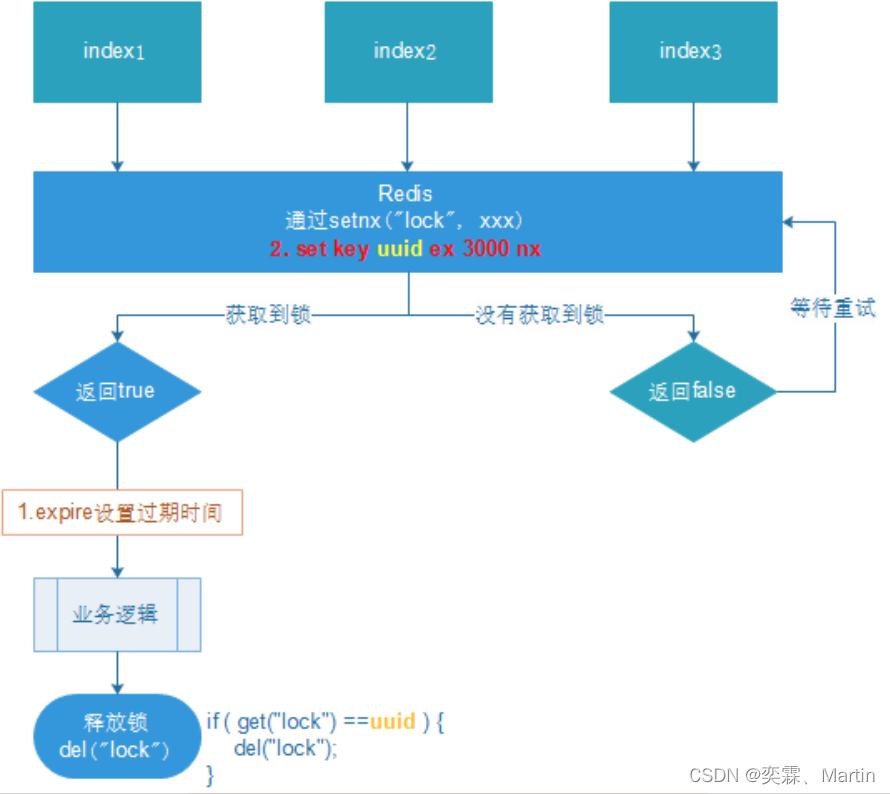
Redis第四讲
目录 四、Redis04 4.1 Redis集群应用场景 4.2 集群 4.2.1 基本原理 4.2.2 主从复制的作用 4.3 配置集群(一台虚拟机) 4.3.1 规划网络 4.3.2 创建节点 4.3.3 创建目录 4.3.4 配置redis7001.conf 4.3.5 配置其余文件 4.3.6 后台启动redis 4.3…...

Linux Ubuntu 软件安装与卸载
文章目录1 下载 deb 安装包后安装2 清理安装包3 卸载安装2 Ubuntu升级某个软件参考:1 下载 deb 安装包后安装 进入下载位置,执行 terminal sudo dpkg -i *.deb推荐sudo apt install *.deb 2 清理安装包 sudo apt-get install 会将下载的文件放在 /var…...
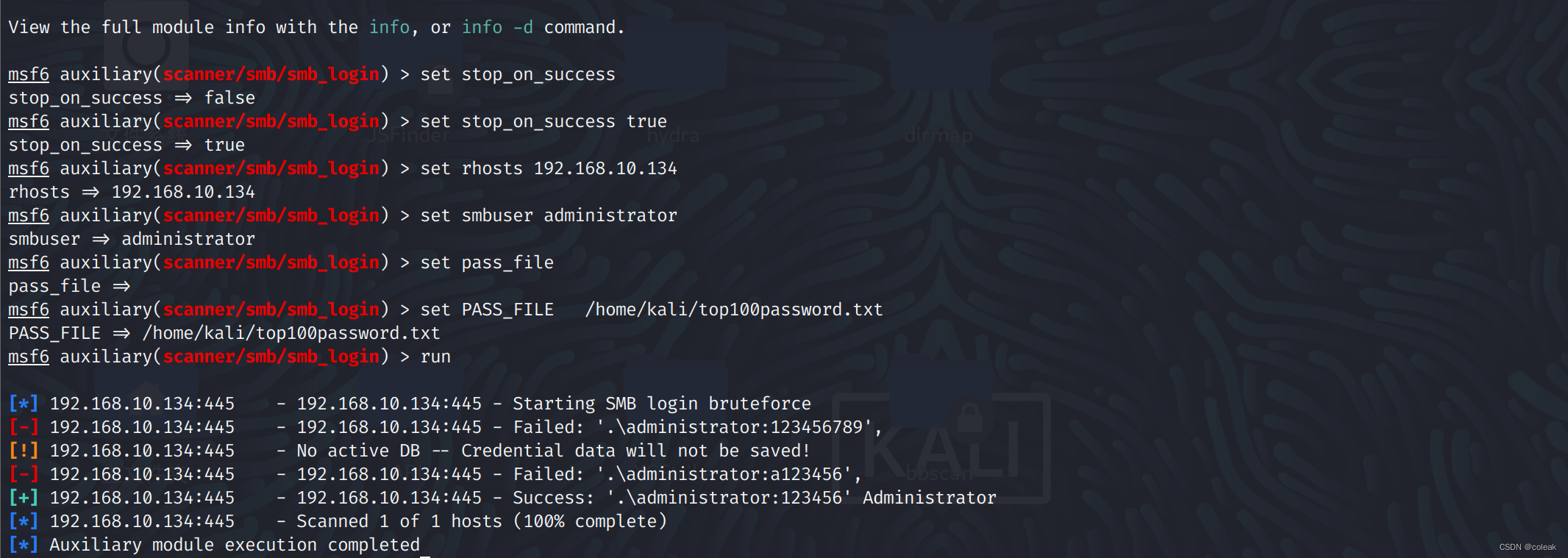
metasploit穷举模块
目录 工具介绍 常用模块 参数介绍 工具使用 工具介绍 Metasploit框架(Metasploit Framework, MSF)是一个开源工具, 旨在方便渗透测试,它是由Ruby程序语言编写的模板化框架,具有很好的扩展性,便于渗透测试人员开发、使用定制的…...

day35 贪心算法 | 435、无重叠区间 763、划分字母区间 56、合并区间
题目 435、无重叠区间 给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。 注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。 示例 1: 输入: [ [1,2], [2,3], […...
C++Primer15.5节练习
练习15.18: Base* p &d1:合法 p &d2:不合法,只有当派生类公有地继承基类时,用户代码才能使用派生类向基类的转换 p &d3:不合法,只有当派生类公有地继承基类时࿰…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
