链式前向星介绍以及原理
1 链式前向星
1.1 简介
链式前向星可用于存储图,本质上是一个静态链表。
一般来说,存储图常见的两种方式为:
- 邻接矩阵
- 邻接表
邻接表的实现一般使用数组实现,而链式前向星就是使用链表实现的邻接表。
1.2 出处
出处可参考此处。
2 原理
链式前向星有两个核心数组:
pre数组:存储的是边的前向链接关系last数组:存储的是某个点最后一次出现的边的下标
感觉云里雾里对吧,可以看看下面的详细解释。
2.1 pre数组
pre数组存储的是一个链式的边的前向关系,下标以及取值如下:
pre数组的下标:边的下标pre数组的值:前向边的下标,如果没有前向边,取值-1
这里的前向边是指,如果某个点,作为起始点,已经出现过边x,那么,遍历到以该点作为起始点的下一条边y时,边y的前向边就是边x。
更新pre数组的时候,会遍历每一条边,更新该边对应的前向边。
比如,输入的有向边如下:
n=6 // 顶点数
[[0,1],[1,3],[3,5],[2,4],[2,3],[0,5],[0,3],[3,4]] // 边
那么:
- 对于第一条边,下标为
0,那么会更新pre[0]的值,边为0->1,而起始点点0还没有出现过前向边,那么pre[0]=-1。这样就建立了边0->-1的一个链接关系,也就是说,对于起始点点0,它只有边0这一条边 - 对于第二条边,下标为
1,那么会更新pre[1]的值,边为1->3,而起始点点1还没有出现过前向边,那么pre[1]=-1。这样就建立了边1->-1的一个链接关系,也就是说,对于起始点点1,它只有边1这一条边 - 对于第三条边,下标为
2,那么会更新pre[2]的值,边为3->5,而起始点点3还没有出现过前向边,那么pre[2]=-1。这样就建立了边2->-1的一个链接关系,也就是说,对于起始点点3,它只有边2这一条边 - 对于第四条边,下标为
3,那么会更新pre[3]的值,边为2->4,而起始点点2还没有出现过前向边,那么pre[3]=-1。这样就建立了边3->-1的一个链接关系,也就是说,对于起始点点2,它只有边3这一条边 - 对于第五条边,下标为
4,那么会更新pre[4]的值,边为2->3,而起始点点2,已经出现过一条边了,该边的下标是3,也就是前向边为3,那么就会更新pre[4]为前向边的值,也就是pre[4]=3。这样,就建立了边4->3->-1的一个链接关系,也就是对于起始点点2来说,目前有两条边,一条是边4,一条是边3 - 对于第六条边,下标为
5,那么会更新pre[5]的值,边为0->5,而起始点点0,已经出现过一条边了,该边的下标是边0,也就是前向边为0,那么就会更新pre[5]为前向边的值,也就是pre[5]=0。这样,就建立了边5->0->-1的一个链接关系,也就是对于起始点点0来说,目前有两条边,一条是边5,一条是边0 - 对于第七条边,下标为
6,那么会更新pre[6]的值,边为0->3,而起始点点0,已经出现过不止一条边了,最后一次出现的边为边5,也就是前向边为5,那么就会更新pre[6]为前向边的值,也就是pre[6]=5。这样,就建立了边6->5->0->-1的一个链接关系,也就是对于起始点点0来说,已经有三条边了,一条是边6,一条是边5,一条是边0 - 对于第八条边,下标为
7,那么会更新pre[7]的值,边为3->4,而起始点点3,已经出现过一条边了,该边的下标是边2,也就是前向边为2,那么就会更新pre[7]为前向边的值,也就是pre[7]=2。这样,就建立了边7->2->-1的一个链接关系,也就是对于起始点点3来说,目前有两条边,一条是边7,一条是边2
这样,边的链接关系就建立下来了:
点 边的链接关系(边的下标)
0 6->5->0->-1
1 1->-1
2 4->3->-1
3 7->2->-1
4 -1
5 -1
2.2 last数组
last数组存储的是最后一次出现的前向边的下标,下标以及取值如下:
last数组的下标:点last数组的值:最后一次出现的前向边的下标
last数组会将所有值初始化为-1,表示所有的点在没有遍历前都是没有前向边的。
使用上面的数据举例:
n=6 // 顶点数
[[0,1],[1,3],[3,5],[2,4],[2,3],[0,5],[0,3],[3,4]] // 边
last数组会与pre数组一起在遍历边的时候更新:
- 遍历到第一条边:下标为
0,边为0->1,那么会更新以0为起始点的前向边的值,也就是自己,last[0]=0。然后,如果下一次遍历到了以0为起始点的边,比如0->5,那么0->5的前向边就是边0,而边0就存储在last[0]中,下次需要的时候直接取last[0]即可 - 遍历到第二条边:下标为
1,边为1->3,那么会更新以1为起始点的最后一次出现的前向边的值,也就是last[1]=1 - 遍历到第三条边:下标为
2,边为3->5,那么会更新以3为起始点的最后一次出现的前向边的值,也就是last[3]=2 - 遍历到第四条边:下标为
3,边为2->4,那么会更新以2为起始点的最后一次出现的前向边的值,也就是last[2]=3 - 遍历到第五条边:下标为
4,边为2->3,那么会更新以2为起始点的最后一次出现的前向边的值,也就是last[2]=4 - 遍历到第六条边:下标为
5,边为0->5,那么会更新以0为起始点的最后一次出现的前向边的值,也就是last[0]=5 - 遍历到第七条边:下标为
6,边为0->3,那么会更新以0为起始点的最后一次出现的前向边的值,也就是last[0]=6 - 遍历到第八条边:下标为
7,边为3->4,那么会更新以3为起始点的最后一次出现的前向边的值,也就是last[3]=7
在遍历每条边的时候,会先从last数组取值并赋给pre去生成链接关系,然后更新last数组中对应起始点的值为当前的边的下标。
3 代码
3.1 生成数组
生成last以及pre数组:
public class Solution {private int[] pre;private int[] last;private void buildGraph(int n, int[][] edge) {int edgeCount = edge.length;pre = new int[edgeCount];last = new int[n];Arrays.fill(last, -1);for (int i = 0; i < edgeCount; i++) {int v0 = edge[i][0];pre[i] = last[v0];last[v0] = i;}}
}
pre的范围与边数有关,而last的范围与点数有关。一开始需要初始化last数组为-1,然后遍历每一条边:
- 遍历边时仅需要知道起始点即可,因为终点可以通过边的下标获取到,不需要存储
- 遍历时首先更新
pre数组为最后一次出现的前向边的下标,也就是对应起始点的last数组的值 - 最后更新
last数组,对应起始点的值更新为当前边的下标
3.2 遍历
public class Solution {private int[] pre;private int[] last;private void visit(int n, int[][] edge) {for (int i = 0; i < n; i++) {System.out.println("当前顶点:" + i);for (int lastEdge = last[i]; lastEdge != -1; lastEdge = pre[lastEdge]) {System.out.println(edge[lastEdge][0] + "->" + edge[lastEdge][1]);}}}
}
遍历从点开始,首先通过last数组取得最后一条出现的前向边的下标,然后遍历该边,最后通过pre数组更新前向边,也就是对链接关系进行遍历。
3.3 完整测试代码
import java.util.Arrays;public class Solution {private int[] pre;private int[] last;private void buildGraph(int n, int[][] edge) {int edgeCount = edge.length;pre = new int[edgeCount];last = new int[n];Arrays.fill(last, -1);for (int i = 0; i < edgeCount; i++) {int v0 = edge[i][0];pre[i] = last[v0];last[v0] = i;}}private void visit(int n, int[][] edge) {for (int i = 0; i < n; i++) {System.out.println("当前顶点:" + i);for (int lastEdge = last[i]; lastEdge != -1; lastEdge = pre[lastEdge]) {System.out.println(edge[lastEdge][0] + "->" + edge[lastEdge][1]);}}}public void build() {int n = 6;int[][] edge = {{0, 1}, {1, 3}, {3, 5}, {2, 4}, {2, 3}, {0, 5}, {0, 3}, {3, 4}};buildGraph(n, edge);visit(n, edge);}
}
输出:
当前顶点:0
0->3
0->5
0->1
当前顶点:1
1->3
当前顶点:2
2->3
2->4
当前顶点:3
3->4
3->5
当前顶点:4
当前顶点:5
可以看到输出的顺序与edge数组是相反的,比如edge数组中的以0为起始点的边的顺序为0->1,0->5,0->3,而输出顺序为0->3,0->5,0->1,这是因为pre的前向链接关系,生成pre数组的时候,采用的是类似链表中的“头插法”生成。
如果想要和原来的顺序保持一致,可以将edge数组反转再生成pre和last数组:
private void buildGraph(int n, int[][] edge) {int edgeCount = edge.length;int[][] reverseEdge = new int[edgeCount][2];for (int i = 0; i < edgeCount; i++) {reverseEdge[i] = edge[edgeCount - i - 1];}pre = new int[edgeCount];last = new int[n];Arrays.fill(last, -1);for (int i = 0; i < edgeCount; i++) {int v0 = reverseEdge[i][0];pre[i] = last[v0];last[v0] = i;}
}
然后遍历edge数组的时候也需要反转:
private void visit(int n, int[][] edge) {int edgeCount = edge.length;int[][] reverseEdge = new int[edgeCount][2];for (int i = 0; i < edgeCount; i++) {reverseEdge[i] = edge[edgeCount - i - 1];}for (int i = 0; i < n; i++) {System.out.println("当前顶点:" + i);for (int lastEdge = last[i]; lastEdge != -1; lastEdge = pre[lastEdge]) {System.out.println(reverseEdge[lastEdge][0] + "->" + reverseEdge[lastEdge][1]);}}
}
测试代码不变:
public void build() {int n = 6;int[][] edge = {{0, 1}, {1, 3}, {3, 5}, {2, 4}, {2, 3}, {0, 5}, {0, 3}, {3, 4}};buildGraph(n, edge);visit(n, edge);
}
输出:
当前顶点:0
0->1
0->5
0->3
当前顶点:1
1->3
当前顶点:2
2->4
2->3
当前顶点:3
3->5
3->4
当前顶点:4
当前顶点:5
可以看到输出顺序和edge对应的边的顺序一致了。
4 疑问
4.1 为什么叫pre数组而不是next数组
笔者看到网上的文章很多都是如下三个数组:
head[u]数组:表示以u作为起点的第一条边的编号next[cnt]数组:表示编号为cnt的边的下一条边,这条边与cnt同一个起点to[cnt]数组:表示编号为cnt的边的终点
其中to[cnt]数组在本篇文章中没有实现,因为已经有edge数组存储了。
head[u]数组,相当于本篇文章中的last数组,而next[cnt]数组,相当于本篇文章中的pre数组。
那么为什么取不同的名字?
只是笔者认为,从自己的角度出发,这样好比较理解。如果还是觉得难理解,可以到文末的参考链接处看一下其他文章。
4.2 这个东西到底有什么用
链式前向星能做的题目,一般来说邻接表也能做。链式前向星,不是用来帮你AC题目来的,不是说某道题非得用它。它是用来帮助你在AC的基础上,进一步提高效率。链式前向星是一种优化手段,它只是帮助你优化,而不是学习了它,就能AC题目。
5 参考
- Malash’s Blog-链式前向星及其简单应用
- CSDN-链式前向星–最通俗易懂的讲解
- 知乎-链式前向星
相关文章:

链式前向星介绍以及原理
1 链式前向星 1.1 简介 链式前向星可用于存储图,本质上是一个静态链表。 一般来说,存储图常见的两种方式为: 邻接矩阵邻接表 邻接表的实现一般使用数组实现,而链式前向星就是使用链表实现的邻接表。 1.2 出处 出处可参考此…...

jenkins 安装 -适用于在线安装 后续写个离线安装的
jenkins安装1.下载jenkins2.安装启动3.附件卸载jdk的命令4.配置jenkins一、在jenkins配置文件中配置jdk环境变量二、修改jenkins默认的操作用户1.下载jenkins jenkins官网下载 https://www.jenkins.io/ 点击下载 我是centos系统所以选择centos,点击后按着官方提供…...
【C++】再谈vscode界面调试C++程序(linux) - 知识点目录
再谈vscode界面调试C程序(linux) 配套文档:vscode界面调试C程序(linux) 命令解释 g -g ../main.cpp 编译main.cpp文件; -g:生成调试信息。编译器会在可执行文件中嵌入符号表和源代码文件名&…...

蚂蚁感冒---第五届蓝桥杯真题
目录 题目链接 题目描述 分析: 代码: y总综合 666 题目链接 1211. 蚂蚁感冒 - AcWing题库 题目描述 分析: y总真牛逼,掉头等价于穿过,以第一个点为分界点,分别判断 代码: (自…...
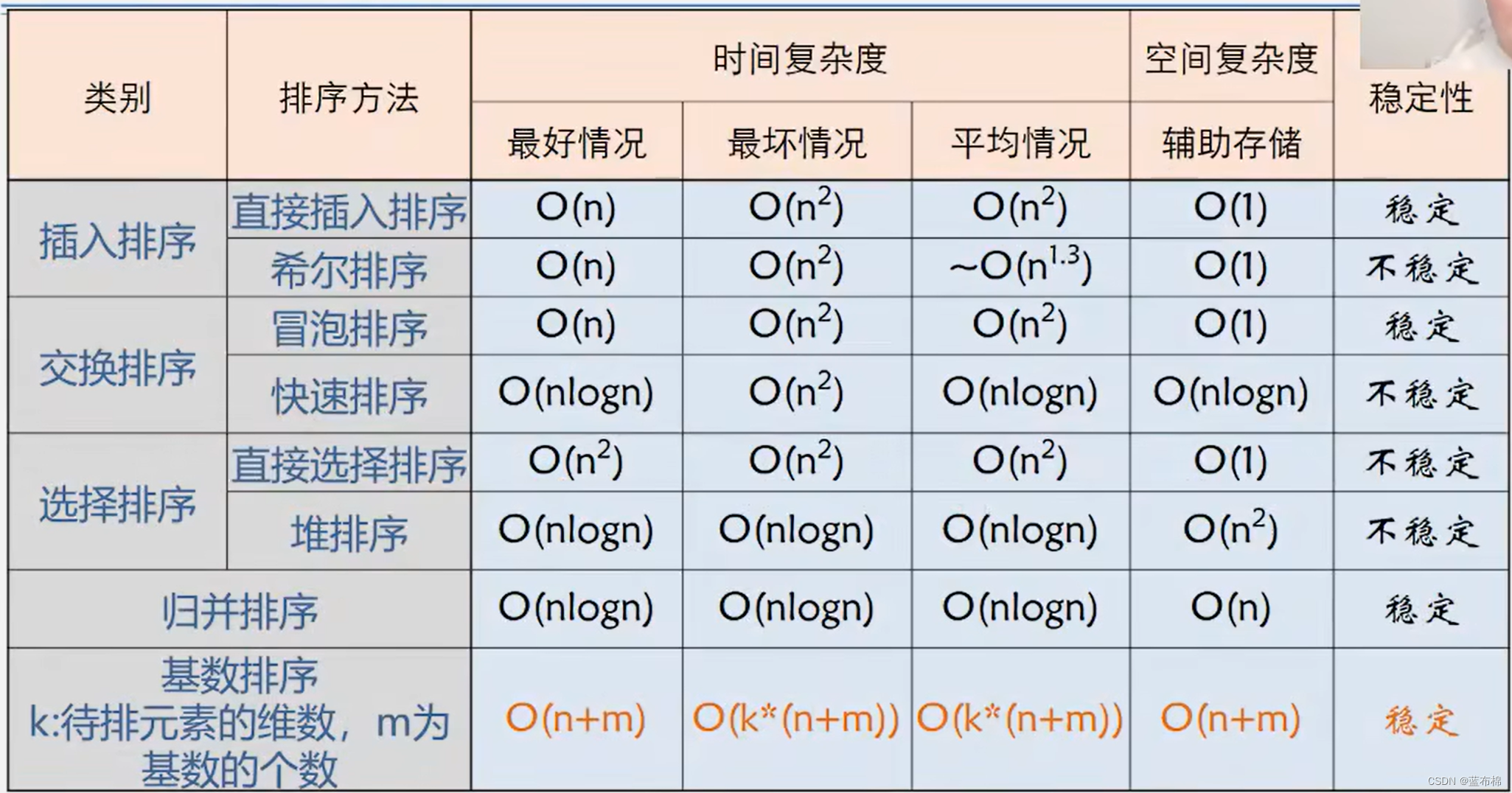
常见排序算法--Java实现
常见排序算法--Java实现插入排序直接插入排序折半插入排序希尔排序交换排序冒泡排序快速排序选择排序直接选择排序堆排序归并排序基数排序各种排序方法比较在网上找了些排序算法的资料。此篇笔记本人总结比较,简单注释,觉得比较好理解,且相对…...

算法笔记(九)—— 暴力递归
暴力递归(尝试) 1. 将问题转化为规模缩小了的同类问题子问题 2. 有明确的不需要的继续递归的条件 3. 有当得到子问题结果之后的决策过程 4. 不记录每一个子问题的解 Question:经典汉诺塔问题 1. 理解清楚,基础三个圆盘的移动…...

Flask框架学习记录
Flask项目简要 项目大致结构 flaskDemo1 ├─static ├─templates └─app.py app.py # 从flask这个包中导入Flask类 from flask import Flask# 使用Flask类创建一个app对象 # __name__:代表当前app.py这个模块 # 1.以后出现bug,可以帮助快速定位 # 2.对于寻找…...

【Opencv 系列】 第6章 人脸检测(Haar/dlib) 关键点检测
本章内容 1.人脸检测,分别用Haar 和 dlib 目标:确定图片中人脸的位置,并画出矩形框 Haar Cascade 哈尔级联 核心原理 (1)使用Haar-like特征做检测 (2)Integral Image : 积分图加速特征计算 …...

信源分类及数学模型
本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:information-theory】,需要的朋友们自取。或者公众号【AIShareLab】回复 信息论 也可获取。 文章目录信源分类按照信源…...
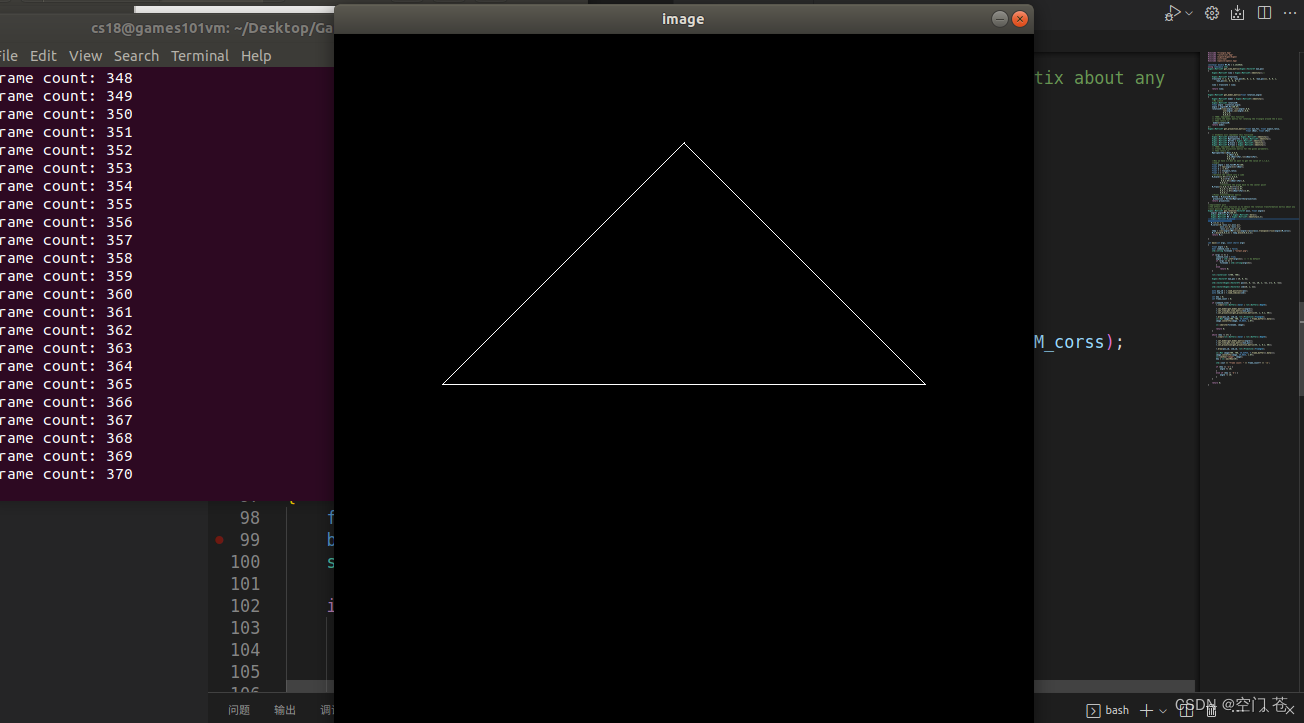
Games101-202作业1
一. 将模型从模型空间变换到世界空间下 在这个作业下,我们主要进行旋转的变换。 二.视图变换 ,将相机移动到坐标原点,同时保证物体和相机进行同样的变换(这样对形成的图像没有影响) 在这个作业下我们主要进行摄像机的平移变换&am…...
Linux系统之终端管理命令的基本使用
Linux系统之终端管理命令的基本使用一、检查本地系统环境1.检查系统版本2.检查系统内核版本二、终端介绍1.终端简介2.Linux终端简介3.终端的发展三、终端的相关术语1.终端模拟器2.tty终端3.pts终端4.pty终端5.控制台终端四、终端管理命令ps1.直接使用ps命令2.列出登录详细信息五…...

【Mongoose笔记】MQTT 服务器
【Mongoose笔记】MQTT 服务器 简介 Mongoose 笔记系列用于记录学习 Mongoose 的一些内容。 Mongoose 是一个 C/C 的网络库。它为 TCP、UDP、HTTP、WebSocket、MQTT 实现了事件驱动的、非阻塞的 API。 项目地址: https://github.com/cesanta/mongoose学习 下面…...

数据结构概述
逻辑结构 顺序存储 随机访问是可以通过下标取到任意一个元素,即数组的起始位置下标 链式存储 链式存储是不连续的,比如A只保留了当前的指针,那么怎么访问到B和C呢 每个元素不仅存储自己的值还使用额外的空间存储指针指向下一个元素的地址&a…...
【前端】Vue3+Vant4项目:旅游App-项目总结与预览(已开源)
文章目录项目预览首页Home日历:日期选择开始搜索位置选择上搜索框热门精选-房屋详情1热门精选-房屋详情2其他页面项目笔记项目代码项目数据项目预览 启动项目: npm run dev在浏览器中F12: 首页Home 热门精选滑动到底部后会自动加载新数据&a…...
51单片机蜂鸣器的使用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、有源蜂鸣器和无源蜂鸣器的区别二、代码编写总结前言 本文旨在介绍如何使用51单片机驱动蜂鸣器。 一、有源蜂鸣器和无源蜂鸣器的区别 有源蜂鸣器是一种电子…...

算法练习-链表(二)
算法练习-链表(二) 文章目录算法练习-链表(二)1. 奇偶链表1.1 题目1.2 题解2. K 个一组翻转链表2.1 题目2.2 题解3. 剑指 Offer 22. 链表中倒数第k个节点3.1 题目3.2 题解3.2.1 解法13.2.2 解法24. 删除链表的倒数第 N 个结点4.1 …...
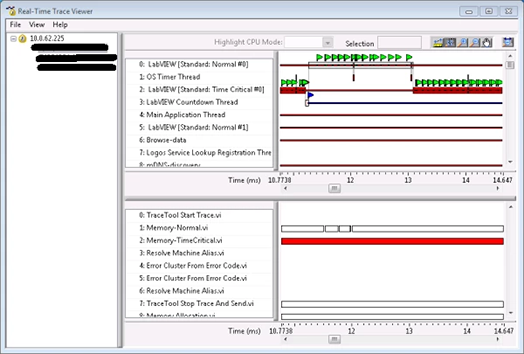
LabVIEW使用实时跟踪查看器调试多核应用程序
LabVIEW使用实时跟踪查看器调试多核应用程序随着多核CPU的推出,开发人员现在可以在LabVIEW的帮助下充分利用这项新技术的功能。并行编程在为多核CPU开发应用程序时提出了新的挑战,例如同步多个线程对共享内存的并发访问以及处理器关联。LabVIEW可自动处理…...

【go语言grpc之client端源码分析二】
go语言grpc之server端源码分析二DialContextparseTargetAndFindResolvergetResolvernewCCResolverWrapperccResolverWrapper.UpdateStatecc.maybeApplyDefaultServiceConfigccBalancerWrapper.updateClientConnState上一篇文章分析了ClientConn的主要结构体成员,然后…...

centos7安装RabbitMQ
1、查看本机基本信息 查看Linux发行版本 uname -a # Linux VM-0-8-centos 3.10.0-1160.11.1.el7.x86_64 #1 SMP Fri Dec 18 16:34:56 UTC 2020 x86_64 x86_64 x86_64 GNU/Linux cat /etc/redhat-release # CentOS Linux release 7.9.2009 (Core)2、创建创建工作目录 mkdir /…...
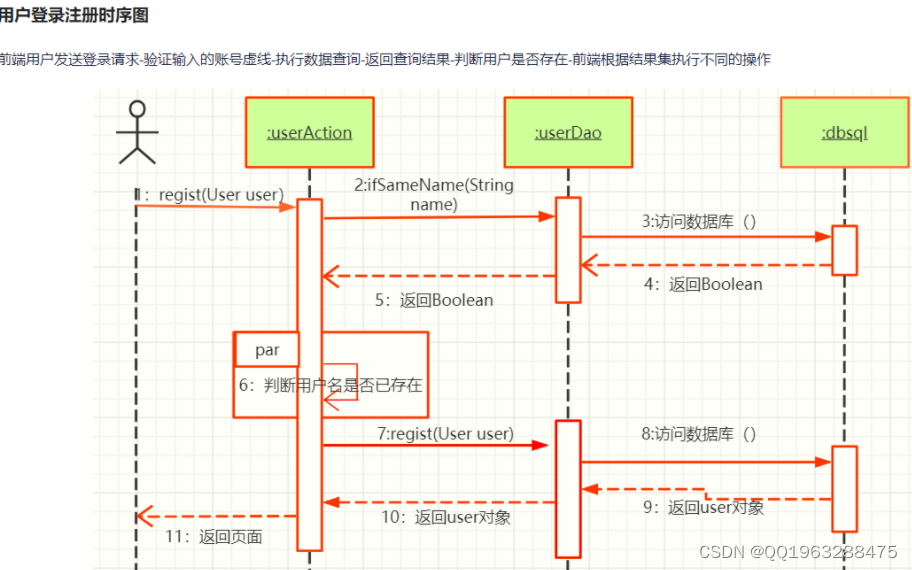
node基于springboot 口腔卫生防护口腔牙科诊所管理系统
目录 1 绪论 1 1.1课题背景 1 1.2课题研究现状 1 1.3初步设计方法与实施方案 2 1.4本文研究内容 2 2 系统开发环境 4 2.1 JAVA简介 4 2.2MyEclipse环境配置 4 2.3 B/S结构简介 4 2.4MySQL数据库 5 2.5 SPRINGBOOT框架 5 3 系统分析 6 3.1系统可行性分析 6 3.1.1经济可行性 6 3.…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
