代码随想录训练营day56| 583. 两个字符串的删除操作 72. 编辑距离
@TOC
前言
代码随想录算法训练营day56
一、Leetcode 583. 两个字符串的删除操作
1.题目
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
示例 1:
输入: word1 = "sea", word2 = "eat" 输出: 2 解释: 第一步将 "sea" 变为 "ea" ,第二步将 "eat "变为 "ea"
示例 2:
输入:word1 = "leetcode", word2 = "etco" 输出:4
提示:
1 <= word1.length, word2.length <= 500
word1 和 word2 只包含小写英文字母来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/delete-operation-for-two-strings
2.解题思路
方法一:最长公共子序列
给定两个字符串 word1word1 和 word2word2,分别删除若干字符之后使得两个字符串相同,则剩下的字符为两个字符串的公共子序列。为了使删除操作的次数最少,剩下的字符应尽可能多。当剩下的字符为两个字符串的最长公共子序列时,删除操作的次数最少。因此,可以计算两个字符串的最长公共子序列的长度,然后分别计算两个字符串的长度和最长公共子序列的长度之差,即为两个字符串分别需要删除的字符数,两个字符串各自需要删除的字符数之和即为最少的删除操作的总次数。
关于最长公共子序列,请读者参考「1143. 最长公共子序列」。计算最长公共子序列的长度的方法见「1143. 最长公共子序列的官方题解」,这里不再具体阐述。
假设字符串 word1word1 和 word2word2 的长度分别为 mm 和 nn,计算字符串 word1word1 和 word2word2 的最长公共子序列的长度,记为 lcslcs,则最少删除操作次数为 m−lcs+n−lcsm−lcs+n−lcs。
3.代码实现
```java class Solution { public int minDistance(String word1, String word2) { int m = word1.length(), n = word2.length(); int[][] dp = new int[m + 1][n + 1]; for (int i = 1; i <= m; i++) { char c1 = word1.charAt(i - 1); for (int j = 1; j <= n; j++) { char c2 = word2.charAt(j - 1); if (c1 == c2) { dp[i][j] = dp[i - 1][j - 1] + 1; } else { dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); } } } int lcs = dp[m][n]; return m - lcs + n - lcs; } }
```
二、Leetcode 72. 编辑距离
1.题目
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符示例 1:
输入:word1 = "horse", word2 = "ros" 输出:3 解释: horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution" 输出:5 解释: intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')
提示:
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/edit-distance
2.解题思路
方法一:动态规划
思路和算法
我们可以对任意一个单词进行三种操作:
插入一个字符;删除一个字符;替换一个字符。题目给定了两个单词,设为 A 和 B,这样我们就能够六种操作方法。
但我们可以发现,如果我们有单词 A 和单词 B:
对单词 A 删除一个字符和对单词 B 插入一个字符是等价的。例如当单词 A 为 doge,单词 B 为 dog 时,我们既可以删除单词 A 的最后一个字符 e,得到相同的 dog,也可以在单词 B 末尾添加一个字符 e,得到相同的 doge;同理,对单词 B 删除一个字符和对单词 A 插入一个字符也是等价的;对单词 A 替换一个字符和对单词 B 替换一个字符是等价的。例如当单词 A 为 bat,单词 B 为 cat 时,我们修改单词 A 的第一个字母 b -> c,和修改单词 B 的第一个字母 c -> b 是等价的。这样以来,本质不同的操作实际上只有三种:
在单词 A 中插入一个字符;在单词 B 中插入一个字符;修改单词 A 的一个字符。这样以来,我们就可以把原问题转化为规模较小的子问题。我们用 A = horse,B = ros 作为例子,来看一看是如何把这个问题转化为规模较小的若干子问题的。
在单词 A 中插入一个字符:如果我们知道 horse 到 ro 的编辑距离为 a,那么显然 horse 到 ros 的编辑距离不会超过 a + 1。这是因为我们可以在 a 次操作后将 horse 和 ro 变为相同的字符串,只需要额外的 1 次操作,在单词 A 的末尾添加字符 s,就能在 a + 1 次操作后将 horse 和 ro 变为相同的字符串;在单词 B 中插入一个字符:如果我们知道 hors 到 ros 的编辑距离为 b,那么显然 horse 到 ros 的编辑距离不会超过 b + 1,原因同上;修改单词 A 的一个字符:如果我们知道 hors 到 ro 的编辑距离为 c,那么显然 horse 到 ros 的编辑距离不会超过 c + 1,原因同上。那么从 horse 变成 ros 的编辑距离应该为 min(a + 1, b + 1, c + 1)。
注意:为什么我们总是在单词 A 和 B 的末尾插入或者修改字符,能不能在其它的地方进行操作呢?答案是可以的,但是我们知道,操作的顺序是不影响最终的结果的。例如对于单词 cat,我们希望在 c 和 a 之间添加字符 d 并且将字符 t 修改为字符 b,那么这两个操作无论为什么顺序,都会得到最终的结果 cdab。
你可能觉得 horse 到 ro 这个问题也很难解决。但是没关系,我们可以继续用上面的方法拆分这个问题,对于这个问题拆分出来的所有子问题,我们也可以继续拆分,直到:
字符串 A 为空,如从 转换到 ro,显然编辑距离为字符串 B 的长度,这里是 2;字符串 B 为空,如从 horse 转换到 ,显然编辑距离为字符串 A 的长度,这里是 5。因此,我们就可以使用动态规划来解决这个问题了。我们用 D[i][j] 表示 A 的前 i 个字母和 B 的前 j 个字母之间的编辑距离。
72_fig1.PNG
如上所述,当我们获得 D[i][j-1],D[i-1][j] 和 D[i-1][j-1] 的值之后就可以计算出 D[i][j]。
D[i][j-1] 为 A 的前 i 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们在 A 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i][j-1] + 1;D[i-1][j] 为 A 的前 i - 1 个字符和 B 的前 j 个字符编辑距离的子问题。即对于 A 的第 i 个字符,我们在 B 的末尾添加了一个相同的字符,那么 D[i][j] 最小可以为 D[i-1][j] + 1;D[i-1][j-1] 为 A 前 i - 1 个字符和 B 的前 j - 1 个字符编辑距离的子问题。即对于 B 的第 j 个字符,我们修改 A 的第 i 个字符使它们相同,那么 D[i][j] 最小可以为 D[i-1][j-1] + 1。特别地,如果 A 的第 i 个字符和 B 的第 j 个字符原本就相同,那么我们实际上不需要进行修改操作。在这种情况下,D[i][j] 最小可以为 D[i-1][j-1]。那么我们可以写出如下的状态转移方程:
若 A 和 B 的最后一个字母相同:D[i][j]=min(D[i][j−1]+1,D[i−1][j]+1,D[i−1][j−1])=1+min(D[i][j−1],D[i−1][j],D[i−1][j−1]−1)D[i][j]=min(D[i][j−1]+1,D[i−1][j]+1,D[i−1][j−1])=1+min(D[i][j−1],D[i−1][j],D[i−1][j−1]−1)若 A 和 B 的最后一个字母不同:D[i][j]=1+min(D[i][j−1],D[i−1][j],D[i−1][j−1])D[i][j]=1+min(D[i][j−1],D[i−1][j],D[i−1][j−1])所以每一步结果都将基于上一步的计算结果,示意如下:
72_fig2.PNG
对于边界情况,一个空串和一个非空串的编辑距离为 D[i][0] = i 和 D[0][j] = j,D[i][0] 相当于对 word1 执行 i 次删除操作,D[0][j] 相当于对 word1执行 j 次插入操作。
综上我们得到了算法的全部流程。
3.代码实现
```java class Solution { public int minDistance(String word1, String word2) { int n = word1.length(); int m = word2.length();
// 有一个字符串为空串if (n * m == 0) {return n + m;}// DP 数组int[][] D = new int[n + 1][m + 1];// 边界状态初始化for (int i = 0; i < n + 1; i++) {D[i][0] = i;}for (int j = 0; j < m + 1; j++) {D[0][j] = j;}// 计算所有 DP 值for (int i = 1; i < n + 1; i++) {for (int j = 1; j < m + 1; j++) {int left = D[i - 1][j] + 1;int down = D[i][j - 1] + 1;int left_down = D[i - 1][j - 1];if (word1.charAt(i - 1) != word2.charAt(j - 1)) {left_down += 1;}D[i][j] = Math.min(left, Math.min(down, left_down));}}return D[n][m];
}}
```
相关文章:

代码随想录训练营day56| 583. 两个字符串的删除操作 72. 编辑距离
TOC 前言 代码随想录算法训练营day56 一、Leetcode 583. 两个字符串的删除操作 1.题目 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 示例 1: 输入: word1 "sea",…...

神经网络基础-神经网络补充概念-55-为什么是ML策略
“ML策略”(Machine Learning Strategies)是指在解决机器学习问题时,采取的一系列方法、技巧和策略。选择适当的ML策略对于获得高质量的模型和结果非常重要。以下是为什么要考虑ML策略的一些原因: 问题适应性:不同的机…...

C++初阶语法——内部类
前言:内部类,顾名思义是定义在类中的类,许多人会以为它属于外部的类,实际上并不是,它们是两个独立的类,但是内部类受外部类类域的限制。 目录 一.概念二.特性1.内部类和外部类相互独立2.内部类是外部类的友…...
面向对象编程 OOP 多态)
Java基础(十四)面向对象编程 OOP 多态
Java面向对象基础知识笔记(四) 1. 对象数组的使用 在Java中,我们可以创建包含对象的数组。对象数组是一种特殊类型的数组,其中每个元素都是一个对象的引用。你可以将任何类的对象存储在对象数组中,并通过索引来访问和操…...
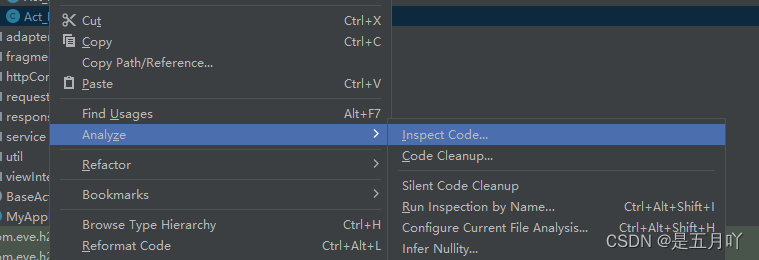
【Android】解决Lint found fatal errors while assembling a release target
报错信息: Android在debug模式下打包没有问题,但是在打包release版本时出现一下问题: 结果图 原因 我项目的原因是因为把正式、测试地址放到代码里了,忘记选中正式环境的地址,导致打正式包有问题;大家如果…...

CF1195E OpenStreetMap 题解
很好的单调队列题。 题目传送门 题目意思: 给定一个 n m n\times m nm 的矩阵,求出所有大小为 a b a\times b ab 的子矩形中的最小值的和。 思路: 通过题目给的要求建立二维数组 h h h。通过单调队列一行一行地扫,将扫出来…...

微信营销系统如何使用效果会更好
微信作为中国最大的社交平台之一,已经成为企业私域营销的重要阵地。在这个庞大的社交网络中,如何使用微信营销系统,将直接影响到企业的营销效果。本文将深入探讨如何更好地利用微信营销系统,以实现更好的私域营销效果。 1. 确定营…...

Linux开机启动程序添加root权限
Linux添加开机启动程序 Debain、Ubuntu系列Linux开机之后会执行/etc/rc.local文件中的命令,所以,如果是想添加登陆用户所具有权限的操作,可以在文件中exit 0之前添加开机自动执行的脚本命令。或者将执行脚本的权限修改为当前登录用户具有执行…...

安卓13解决链接问题
作为Android用户,你可能已经注意到了一个问题——Android 13不再支持PPTP协议。但请别担心,作为一家专业的代理供应商,我们将与你分享解决方案,让你轻松解决L2TP问题,享受到高水平的连接体验。本文将为你提供实用的操作…...

《乡村振兴战略下传统村落文化旅游设计 》在2023年畅销榜排名465位
《乡村振兴战略下传统村落文化旅游设计 》在2023年畅销榜排名465位...
实现一个自动保存高CPU占用现场的简易工具
CPU 使用率在系统监控中是一个非常重要的指标。对于大多数 Web 应用来说,它们往往是 IO 密集型的,因此只会在某些时刻可能会出现 CPU 突然飙升的情况,随后很快就恢复正常。然而,当收到报警并想要排查问题时,CPU 飙升的…...

易服客工作室:如何在WordPress网站中举办虚拟活动
您是否正在寻找举办和管理虚拟活动的最佳方式? 也许您想在线举行下一次会议或举办有关您的产品和服务的网络研讨会。您可能担心它太贵,或者您没有技术知识来实现它。 在本文中,我们将列出您所需的在线服务的所有设备,并教您…...
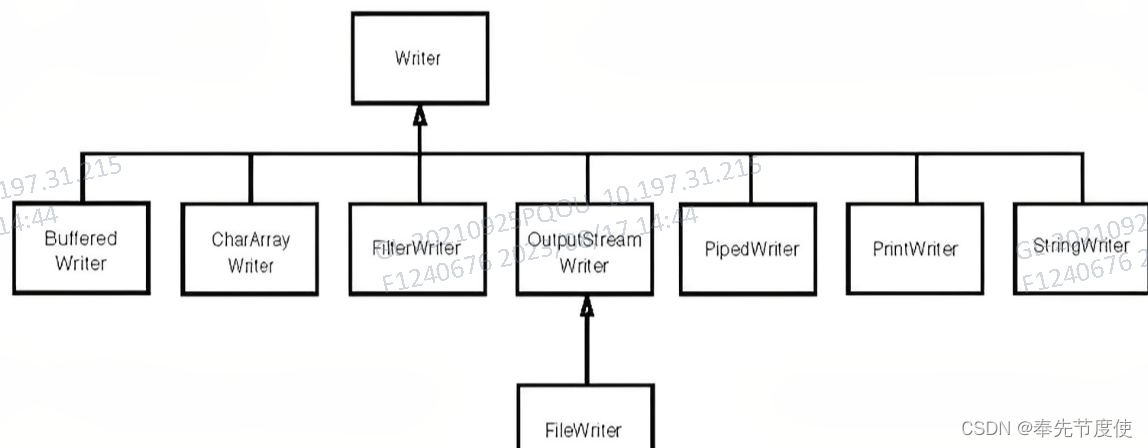
Java IO流(一)IO基础
概述 IO流本质 I/O表示Input/Output,即数据传输过程中的输入/输出,并且输入和输出都是相对于内存来讲Java IO(输入/输出)流是Java用于处理数据读取和写入的关键组件常见的I|O介质包括 文件(输入|输出)网络(输入|输出)键盘(输出)显示器(输出)使用场景 文件拷贝(File&…...

区间覆盖 线段覆盖 二分
4195. 线段覆盖 - AcWing题库 P2082 区间覆盖(加强版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 做法: void solve() {int n; cin>>n;vector<array<LL,2>> seg(n);for(auto &t: seg) cin>>t[0]>>…...
:主动模式)
F#奇妙游(20):主动模式
F#中主动模式的三种形式 F#中有一种特殊的模式匹配,叫做主动模式(Active Pattern)。主动模式可以让我们自定义模式匹配的方式,这样可以让我们的代码更加简洁,更加清晰。主动模式有三种形式,分别是…...

OLED透明屏与传统显示屏的区别:探索未来视觉体验的新里程碑
OLED透明屏作为一种新兴的显示技术,与传统显示屏相比,具有许多独特的特点和优势。 那么,在这篇文章中,尼伽便通过比较OLED透明屏和传统显示屏的区别,包括透明性、对比度、色彩表现力、节能环保等方面,为读…...
打开软件提示mfc100u.dll缺失是什么意思?要怎么处理?
当你打开某个软件或者运行游戏,系统提示mfc100u.dll丢失,此时这个软件或者游戏根本无法运行。其实,mfc100u.dll是动态库文件,它是VS2010编译的软件所产生的,如果电脑运行程序时提示缺少mfc100u.dll文件,程序…...
)
Python 基础 -- Tutorial(二)
5、数据结构 本章更详细地描述了一些你已经学过的东西,并添加了一些新的东西。 5.1. 更多关于Lists 列表(list)数据类型有更多的方法。下面是列表对象的所有方法: list.append(x) 在列表末尾添加一项。相当于a[len(a):] [x]。 list.extend(iterable) 通过添加可…...

11 迭代器|生成器|协程
文章目录 迭代器可迭代对象可迭代对象的本质iter()函数与 next()函数迭代器 Iterator样例 for...in...循环的本质使用的场景--斐波那契数列list和tuple也可以接收可迭代对象 生成器简介创建生成器方法一方法二总结 使用 send 唤醒 协程协程和线程差异简单实现协程greenletgeven…...

“第三方支付”详解!
第三方支付是什么?第三方支付的解释 中央银行官方解释:是与产品所在国和主要外资银行签订合同、具有一定实力和信誉保障的第三方独立机构提供的交易支持平台。在通过第三方支付平台进行的交易中,买方购买货物后,买方使用第三方平台…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
