物理公式分类
(99+ 封私信 / 81 条消息) 定义式和决定式有什么区别,怎么区分? - 知乎 (zhihu.com)
1、首先,定义一个物理符号(物理量)来表征物理世界最直观/最基本的物理现象,例如,长度(米)、质量(千克)、时间(秒)、电流(安培)、热力学温度(开尔文)、物质的量(摩尔)和发光强度(坎德拉) (七个基本物理量)
基本物理量_百度百科 (baidu.com),每个物理量有其基本的定义
2、定义式:定义式用于给出物理量的定义或描述,是人在观察到一些物理现象的相关性时,定义出的一些中间量or关系量,用于描述物理量(现象)之间的关系,但不是物理现象产生的原因。
定义式就是这个物理量出现之初,人们为了赋予这个物理量物理含义而定义出来的等式。定义式是以人的意志为转移的,需要死记硬背。
(这种公式表达了物理量之间的定义关系。它们通过将一个物理量定义为其他物理量的函数,来描述它们之间的关系。例如,动量的定义式是p = mv,其中p表示动量,m表示物体的质量,v表示物体的速度。定义式通常用于引入新的物理量或给出物理量的基本概念。)
3、决定式说明了物理量与其他因素之间的因果关系,什么量是原因,什么是结果。
这种公式描述了物理现象之间的确定性关系。它们表示了一个物理量如何决定另一个物理量,通常是通过实验观测或理论推导得出的。例如,牛顿第二定律F = ma就是一个决定式,它说明了物体的加速度是由作用于它的力和物体的质量决定的。决定式在解决具体问题和预测实验结果时非常有用。
电生磁,磁生电,互为因果!!!
4、演算式(Derivative):这种公式是通过对已知公式进行推导或变换得到的。演算式可以用于简化问题的求解、推导出其他相关公式,或者给出更一般性的描述(一般关系式)。例如,从速度的定义式v = ds/dt可以通过对位移s进行微分,得到加速度的定义式a = d²s/dt²。演算式在深入研究物理问题和推导新的物理关系时非常有用。
计算式通常是对特定问题进行计算的公式。它们适用范围较窄,只能用于特定类型的问题。例如,位移的计算式是 s = vt,其中 s 表示位移,v 表示速度,t 表示时间。这个公式只适用于计算匀速直线运动的位移。当涉及其他类型的运动时,可能需要使用不同的公式。因此,在使用计算式时,我们需要清楚地了解所涉及的物理情境,并选择正确的公式进行计算。
在物理学中,我们通常将表示计算的公式称为计算式,而将表示演算或推导的公式称为演算式。
计算式是已经被验证和确认的,用于计算物理量之间关系的公式。这些公式通常是基于实验观测或理论推导得出的,可以直接应用于具体问题的求解。
例如,F = ma、v = v0 + at 和 E = mc² 都是常见的计算式,用于计算力、速度、能量等物理量之间的关系。
演算式则通常用于推导和证明物理定律或关系的过程。它们是基于严格的数学和逻辑推理,通过一系列符号变换或推导步骤来展示出特定结论的形式。
例如,牛顿力学中的推导过程涉及到使用各种演算式,如牛顿第二定律 F = ma、运动学公式、微积分等,从而得出运动方程、轨迹等结果。
总结起来,计算式用于计算和求解具体的物理问题,而演算式则用于推导和探讨物理定律和关系的过程。它们在物理学中都扮演着重要的角色。
(1)物理公式的分类
物理公式分为物理量的定义式,物理量的决定式和一般联系式.
物理量的定义式,如电阻定义式R=U/I,电场强度定义式E=F/q;
物理量的决定式,如电阻R=ρ(l/S);平行板电容器电容C=(εS/4πkd);
(因果式,自己的起的,不要信)
一般联系式,如理想气体状态方程(pV/T)=常量,机械能守恒表达式.
弄清公式属于哪一种类型,对于理解公式中物理量的因果关系,适用条件等具有十分重要的意义.定义式普遍适用,无须条件;决定式指出了物理量决定于什么因素,与这些因素是什么关系,公式中因果关系非常明确,对于理解该物理量的本质十分重要.
(2)因果性
如牛顿第二定律虽然通常写成F=ma的形式,但应明确m、F是原因,a是结果,m、F是自变量,a是函数.这种关系是不能变化的.(力是运动的原因)
(3)矢量性
公式有矢量式,有标量式,如牛顿第二定律F=ma,动量定理Ft=mv′-mv,都是矢量式,它们可以写出相互垂直方向上相应的三个分量式.而机械能守恒之类的标量表达式只能写一个,不能写出相应的分量形式.
(4)对称性
牛顿万有引力公式F=k(m1m2/r3)r中m1、m2位置互换后,表达式不变,这称为公式的对称性.万有引力定律中的这种对称性反映了m1、m2两个物体的平等地位,是万有引力定律的重要特点.具有这种对称性的公式还有库仑定律,透镜成像公式等.发现、认识这种对称性对于理解物理公式的涵义具有很大的帮助.
相关文章:

物理公式分类
(99 封私信 / 81 条消息) 定义式和决定式有什么区别,怎么区分? - 知乎 (zhihu.com) 1、首先,定义一个物理符号(物理量)来表征物理世界最直观/最基本的物理现象,例如,长度(米…...

vue实现登录注册
目录 一、登录页面 二、注册页面 三、配置路由 一、登录页面 <template><div class"login_container" style"background-color: rgb(243,243,243);height: 93.68vh;background-image: url(https://ts1.cn.mm.bing.net/th/id/R-C.f878c96c4179c501a6…...
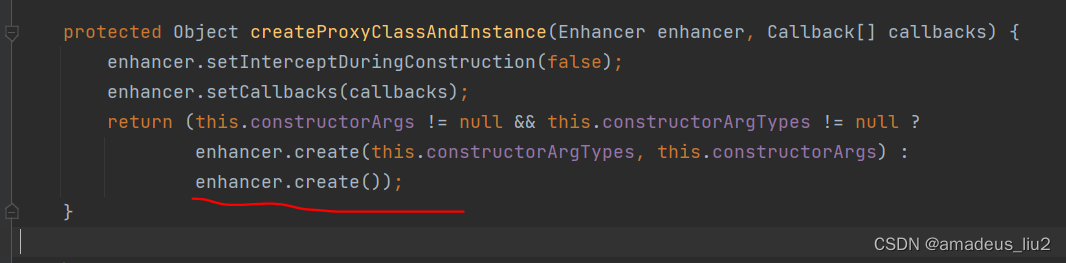
SpringBoot复习:(55)在service类中的方法上加上@Transactional注解后,Spring底层是怎么生成代理对象的?
SpringBoot run方法代码如下: 可以看到它会调用refreshContext方法来刷新Spring容器,这个refreshContext方法最终会调用AbstractApplicationContext的refresh方法,代码如下 如上图,refresh方法最终会调用finisheBeanFactoryInit…...

常用的图像校正方法
在数字图像处理中,常用的校正方法包括明场均匀性校正、查找表(LUT)校正和伽玛(Gamma)校正。这些校正方法分别针对不同的图像问题,可以改善图像质量,提升图像的可读性和可分析性。下面是这三种校…...

AWS security 培训笔记
云计算的好处 Amazon S3 (Storage) Amazon EC2 (Compute) 上图aws 的几个支柱:安全是其中一个啦 其中安全有几个方面 IAMdetection基础架构保护数据保护应急响应 关于云供应商的责任 data center 原来长这样 ,据说非常之隐蔽的 如果有天退役了…...
设计模式之代理模式(Proxy)的C++实现
1、代理模式的提出 在组件的开发过程中,有些对象由于某种原因(比如对象创建的开销很大,或者对象的一些操作需要做安全控制,或者需要进程外的访问等),会使Client使用者在操作这类对象时可能会存在问题&…...
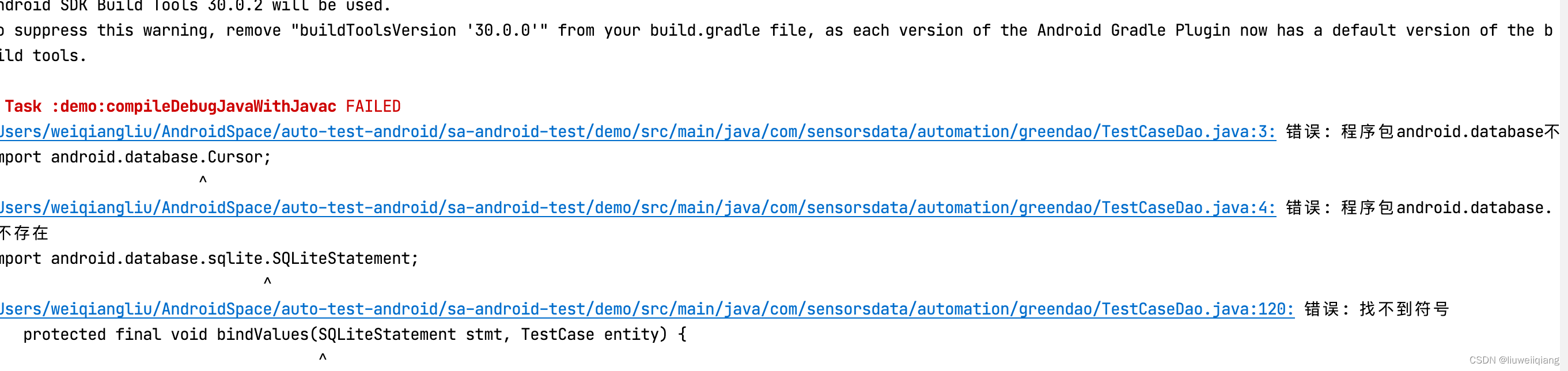
vim 配置环境变量与 JDK 编译器异常
vim 配置环境变量 使用 vim 打开系统中的配置信息(不存在将会创建): vim ~/.bash_profile 以配置两个版本 JDK 为例(前提是已安装 JDK),使用上述命令打开配置信息: 输入法调成英文,输入 i&…...

TiDB v7.1.0 跨业务系统多租户解决方案
本文介绍了 TiDB 数据库的资源管控技术,并通过业务测试验证了效果。资源管控技术旨在解决多业务共用一个集群时的资源隔离和负载问题,通过资源组概念,可以限制不同业务的计算和 I/O 资源,实现资源隔离和优先级调度,提高…...
)
【题解】二叉树中和为某一值的路径(一)
二叉树中和为某一值的路径(一) 题目链接:二叉树中和为某一值的路径(一) 解题思路1:递归 我们或许想记录下每一条从根节点到叶子节点的路径,计算出该条路径的和,但此种思路用递归稍麻烦,我们可以试着把和转换为差&am…...

css中变量和使用变量和运算
变量: 语法:--css变量名:值; --view-theme: #1a99fb; css使用变量: 语法:属性名:var( --css变量名 ); color: var(--view-theme); css运算: 语法:属性名…...

数据结构之线性表的类型运用Linear Lists: 数组,栈,队列,链表
线性表 定义 一个最简单,最基本的数据结构。一个线性表由多个相同类型的元素穿在一次,并且每一个元素都一个前驱(前一个元素)和后继(后一个元素)。 线性表的类型 常见的类型:数组、栈、队列…...

成瘾机制中微生物群的神秘角色
谷禾健康 成瘾是一种大脑疾病,受害者无法控制地对某种物质或行为产生强烈的依赖和渴求,尽管这种行为会产生有害的后果。成瘾包括一系列物质滥用障碍,例如药物、酒精、香烟,过度饮食。近年来,吸毒成瘾急剧上升ÿ…...
arm安装docker与docker-copose
一、银河麒麟Arm64安装docker 1、docker 安装包地址: https://download.docker.com/linux/static/stable 2、解压,然后将docker目录下文件拷贝到/usr/bin里 tar -xf docker-18.09.3.tgz mv docker/* /usr/bin/ 3、准备 docker.service系统配置文件 &…...

9.文件基本操作
第四章 文件管理 9.文件基本操作 “打开文件和关闭文件”与平常鼠标双击打开文件和点击“X”关闭文件是有所不同的。 操作系统在处理open系统调用时主要做了以下两件事情,①根据我们提供的文件存放路径在外存当中找到这个目录对应的目录表&#x…...

【Java】Spring——Bean对象的作用域和生命周期
文章目录 前言一、引出Bean对象的作用域1.普通变量的作用域2.Bean对象的作用域 二、Bean对象的作用域1.Bean对象的6种作用域2.设置Bean对象的作用域 三、Bean对象的生命周期总结 前言 本人是一个普通程序猿!分享一点自己的见解,如果有错误的地方欢迎各位大佬莅临指导,如果你也…...

数字孪生助力智慧水务:科技创新赋能水资源保护
智慧水务中,数字孪生有着深远的作用,正引领着水资源管理和环境保护的创新变革。随着城市化和工业化的不断推进,水资源的可持续利用和管理愈发显得重要,而数字孪生技术为解决这一挑战提供了独特的解决方案。 数字孪生技术…...

css 实现文字横向循环滚动
实现效果 思路 ## 直接上代码,html部分 //我这里是用的uniapp <view class"weather_info_wrap"><view class"weather_info">当前多云,今晚8点转晴,明天有雨,温度32摄氏度。</view><view class&qu…...

VuePress 数学公式支持
前言 博主在为 VuePress1.0 博客添加数学公式支持过程中遇到如下问题 问题一 在配置诸如 markdown-it-texmath,markdown-it-katex,markdown-it-mathjax3 这些插件后遇到 Error: Dynamic require of "XXX" is not supported 问题二 配置插件 vuepress-plugin-ma…...
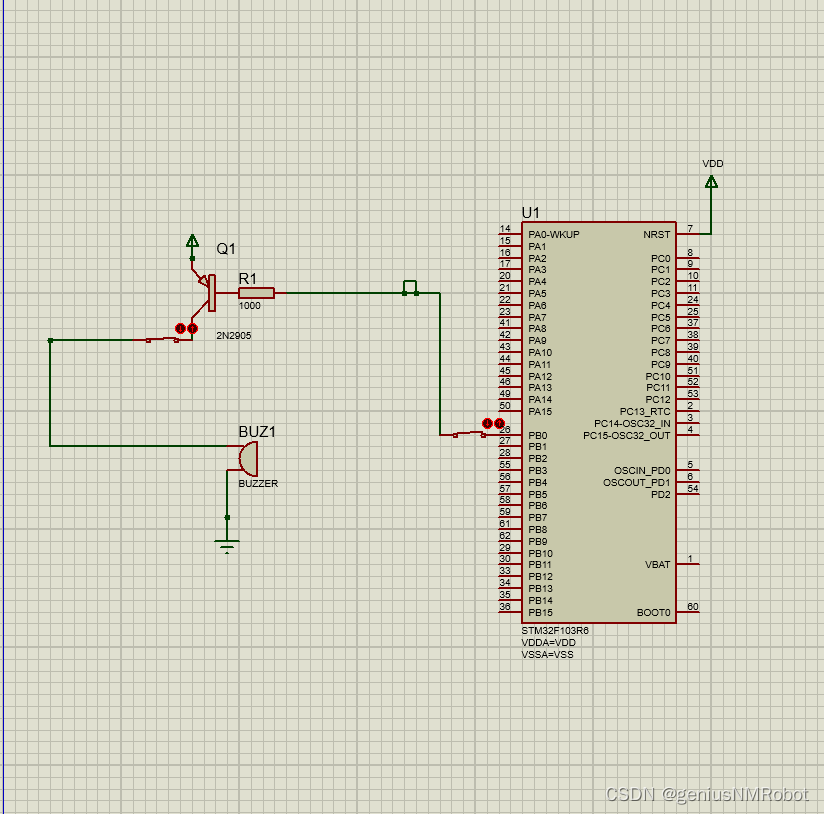
stm32控制蜂鸣器源代码(附带proteus线路图)
说明: 1 PB0输出0时,蜂鸣器发生; 2 蜂鸣器电阻值如果太大会导致电流太小,发不出声音; 3蜂鸣器额定电压需要设置得低一点,可以是2V,但不能高于3V,这更右上角的电阻值有关系&#x…...

selinux
一、selinux的说明 二、selinux的工作原理 三、selinux的启动、关闭与查看 Enforcing和permissive都是临时的,重启还是依据配置文件中,禁用selinux,修改配置文件: 之后重启生效 四、selinux对linux服务的影响...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
