优于立方复杂度的 Rust 中矩阵乘法
优于立方复杂度的 Rust 中矩阵乘法

![]()
迈克·克维特
跟随
更好的编程
143

中途:三次矩阵乘法
一、说明
几年前,我在 C++ 年编写了 Strassen 矩阵乘法算法的实现,最近在 Rust 中重新实现了它,因为我继续学习该语言。这是学习 Rust 性能特征和优化技术的有用练习,因为尽管 Strassen 的算法复杂性优于朴素方法,但它在算法结构中的分配和递归开销中具有很高的常数因子。
- 通用算法
- 换位以获得更好的性能
- 次立方:斯特拉森算法的工作原理
- 排比
- 标杆
- 分析和性能优化
二、通用算法
一般(朴素)矩阵乘法算法是每个人在他们的第一堂线性代数课上学习的三个嵌套循环方法,大多数人会将其识别为 O(n³)
pub fn
mult_naive (a: &Matrix, b: &Matrix) -> Matrix {if a.rows == b.cols {let m = a.rows;let n = a.cols;// preallocatelet mut c: Vec<f64> = Vec::with_capacity(m * m);for i in 0..m {for j in 0..m {let mut sum: f64 = 0.0;for k in 0..n {sum += a.at(i, k) * b.at(k, j);}c.push(sum);}}return Matrix::with_vector(c, m, m);} else {panic!("Matrix sizes do not match");}
} 这种算法很慢,不仅因为三个嵌套循环,还因为按列通过而不是按行的内部循环遍历对于 CPU 缓存命中率来说是可怕的。Bb.at(k, j)
三、换位以获得更好的性能
转置朴素方法允许 B 上的乘法迭代在行而不是列上运行,将矩阵 B 的乘法步幅重新组织为更有利于缓存的格式。从而变成A x BA x B^t

它涉及一个新的矩阵分配(无论如何,在这个实现中)和一个完整的矩阵迭代(一个 O(n²) 操作,更准确地说,这种方法是 O(n³) + O(n²))——我将进一步展示它的性能有多好。它如下所示:
fn multiply_transpose (A: Matrix, B: Matrix):C = new Matrix(A.num_rows, B.num_cols)// Construct transpose; requires allocation and iteration through BB’ = B.transpose()for i in 0 to A.num_rows:for j in 0 to B'.num_rows:sum = 0;for k in 0 to A.num_cols:// Sequential access of B'[j, k] is much faster than B[k, j]sum += A[i, k] * B'[j, k]C[i, j] = sumreturn C 四、次立方:斯特拉森算法的工作原理
要了解 Strassen 算法的工作原理(此处为 Rust 代码),首先考虑矩阵如何用象限表示。要概念化它的外观:

在朴素算法中使用此象限模型,结果矩阵 C 的四个象限中的每一个都是两个子矩阵乘积的总和,总共产生 8 次乘法。

考虑到这八个乘法,每个乘法都在一个块矩阵上运行,其行和列跨度约为 A 和 B 大小的一半,复杂性相同:

斯特拉森算法定义了由这些象限组成的七个中间块矩阵:

仅通过 7 次乘法而不是 8 次乘法计算。这些乘法可以是递归斯特拉森乘法,并可用于组成最终矩阵:

由此产生的亚立方复杂度:

五、排比
中间矩阵 M1 的计算 ...M7 是一个令人尴尬的并行问题,因此也很容易检测算法的并发变体(一旦你开始理解 Rust 关于闭包的规则)。
/*** Execute a recursive strassen multiplication of the given vectors, * from a thread contained within the provided thread pool.*/
fn
_par_run_strassen (a: Vec<f64>, b: Vec<f64>, m: usize, pool: &ThreadPool) -> Arc<Mutex<Option<Matrix>>> {let m1: Arc<Mutex<Option<Matrix>>> = Arc::new(Mutex::new(None));let m1_clone = Arc::clone(&m1);pool.execute(move|| { // Recurse with non-parallel algorithm once we're // in a working threadlet result = mult_strassen(&mut Matrix::with_vector(a, m, m),&mut Matrix::with_vector(b, m, m));*m1_clone.lock().unwrap() = Some(result);});return m1;
}六、标杆
我编写了一些快速的基准测试代码,该代码在不断增加的矩阵维度范围内运行四种算法中的每一种进行几次试验,并报告每种算法的平均时间。
~/code/strassen ~>> ./strassen --lower 75 --upper 100 --factor 50 --trials 2running 50 groups of 2 trials with bounds between [75->3750, 100->5000]x y nxn naive transpose strassen par_strassen
75 100 7500 0.00ms 0.00ms 1.00ms 0.00ms
150 200 30000 6.50ms 4.00ms 4.00ms 1.00ms
225 300 67500 12.50ms 9.00ms 8.50ms 2.50ms
300 400 120000 26.50ms 22.00ms 18.00ms 5.50ms
[...]
3600 4800 17280000 131445.00ms 53683.50ms 21210.50ms 5660.00ms
3675 4900 18007500 141419.00ms 58530.00ms 28291.50ms 6811.00ms
3750 5000 18750000 154941.00ms 60990.00ms 26132.00ms 6613.00ms 然后,我通过以下方式可视化结果:pyplot

此图显示了矩阵从 7.5k 元素 () 到大约 19 万 () 的乘法时间。你可以看到朴素算法在计算上变得不切实际的速度有多快,在高端需要两分半钟。N x M = 75 x 100N x M = 3750 x 5000
相比之下,Strassen 算法的扩展更平滑,并行算法计算两个 19M 个元素的矩阵的结果,而朴素算法只处理 3.6M 个元素所花费的时间。
对我来说最有趣的是算法的性能。如前所述,缓存性能的改进(以牺牲完整矩阵副本为代价)在这些结果中得到了清楚地证明 - 即使使用与该方法渐近等效的算法也是如此。transposenaive
七、分析和性能优化
这个文档是理解 Rust 性能基础知识的绝佳资源。在 Mac OS 上启动并运行仪器进行分析是微不足道的,这要归功于货运仪器的 Rust 指南。这是调查分配行为、CPU 热点和其他事情的绝佳工具。

在此过程中发生了一些变化:
- Strassen 代码通过分而治之策略递归调用自己,但是一旦矩阵达到足够小的大小,其高常数因子使其比一般矩阵算法慢。我发现这个点是大约 64 的行宽或列宽;通过提高吞吐量提高几个因素来增加此阈值
2 - 斯特拉森算法要求矩阵填充到最接近的指数 2;减少这种情况以懒惰地确保矩阵只有偶数行和列 通过减少昂贵的大分配,将吞吐量提高了大约两倍
- 将小矩阵回退算法从 更改为 导致大约 20% 的改进
naivetranspose - 添加和添加到 Cargo.toml 发布构建标志大约提高了 5%。有趣的是,性能持续恶化
codegen-units = 1lto = "thin"lto = “true” - 一丝不苟地删除所有可能的副本大约提高了~10%
Vec - 提供一些提示并删除随机访问查找中的向量边界检查,又提高了大约 20%
#[inline]
/*** Returns the element at (i, j). Unsafe.*/#[inline]pub fn at (&self, i: usize, j: usize) -> f64 {unsafe {return *self.elements.get_unchecked(i * self.cols + j);}}参考资料:
相关文章:

优于立方复杂度的 Rust 中矩阵乘法
优于立方复杂度的 Rust 中矩阵乘法 迈克克维特 跟随 发表于 更好的编程 6 分钟阅读 7月 <> 143 中途:三次矩阵乘法 一、说明 几年前,我在 C 年编写了 Strassen 矩阵乘法算法的实现,最近在 Rust 中重新实现了它,因为我继续…...

CentOS gcc介绍及快速升级
1.gcc介绍 GCC(GNU Compiler Collection)是一个开源的编译器套件,由 GNU(GNUs Not Unix!的递归缩写) 项目开发和维护。它是一个功能强大且广泛使用的编译器,支持多种编程语言,包括 C、C、Objective-C、Fortran、Ada 和…...

IO多路复用中select的TCP服务器模型和poll服务模型
select的TCP服务器模型 服务器端 #include <head.h> #include <sys/types.h> #include <sys/socket.h> #include <arpa/inet.h> #include <unistd.h> #include <sys/select.h> #include <sys/time.h>#define PORT 6666 //1024~4…...

AI工程师招募;60+开发者AI工具清单;如何用AI工具读懂插件源码;开发者出海解读;斯坦福LLM课程 | ShowMeAI日报
👀日报&周刊合集 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🤖 一则AI工程师招募信息:新领域需要新技能 Vision Flow (目的涌现) 是一家基于 AGI 原生技术的创业公司,是全球探…...

Mysql 使用JSON_SEARCH函数 判断多表查询时,某个拼接字段是否包含另外一个字段
场景 两个表管理查询 关联字段为A表id, B表的ids A表id是正常的整数, B的ids是id拼接成的字符类型, 格式是111,222,333这样的. A: B: id ids11 11,22,3322 33,44,5533 …...

C++头文件
C头文件 一般头文件特殊头文件windows.hbits/stdc.h 一般头文件 C头文件是一种包含预定义函数、类和变量声明的文件。它们通常用于在源代码文件中引入外部库或模块的功能。 头文件的作用是提供程序所需的声明信息,以便在源代码文件中使用这些声明。当你在源代码文…...

无脑入门pytorch系列(四)—— scatter_
本系列教程适用于没有任何pytorch的同学(简单的python语法还是要的),从代码的表层出发挖掘代码的深层含义,理解具体的意思和内涵。pytorch的很多函数看着非常简单,但是其中包含了很多内容,不了解其中的意思…...
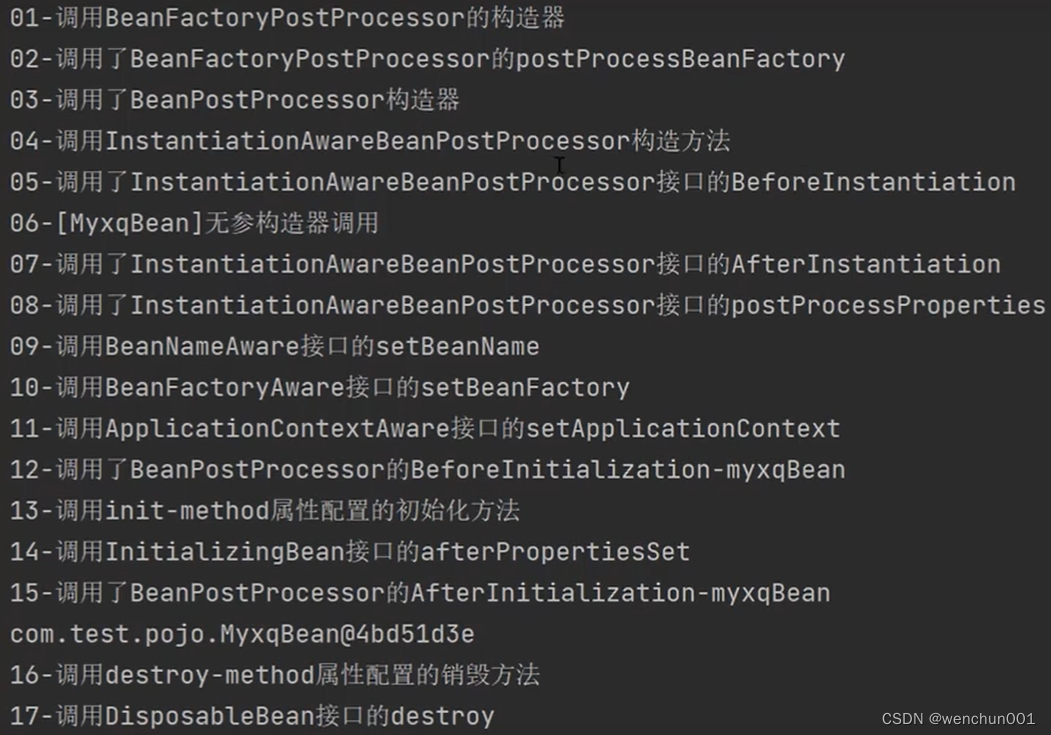
【Spring源码】Spring扩展点及顺序
Spring扩展点及顺序 01-调用BeanFactoryPostProcessor的构造器 02-调用了BeanFactoryPostProcessor的postProcessBeanFactory 03-调用了BeanPostProcessor构造器 04-调用InstantiationAwareBeanPostProcessor构造方法 05-调用了InstantiationAwareBeanPostProcessor接口的Befo…...

广州华锐互动:3D数字孪生开发编辑器助力企业高效开发数字孪生应用
3D数字孪生开发编辑器是一种新兴的技术,它可以帮助企业更好地管理和维护其物联网设备。这些工具可以帮助企业实现对设备的实时监控、故障排除和优化,从而提高生产效率和降低成本。 数字孪生系统是一种将物理世界与数字世界相结合的技术,它可以…...
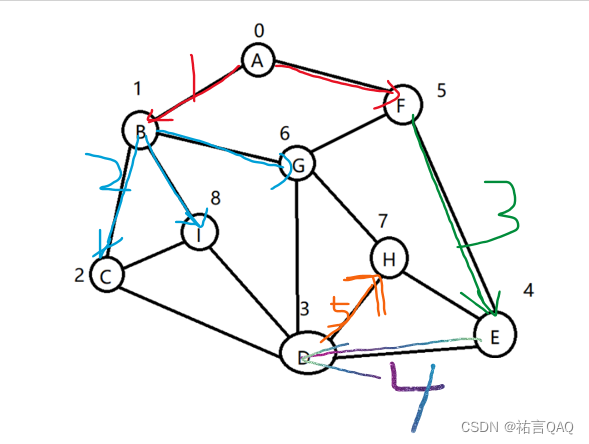
【脚踢数据结构】图(纯享版)
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,Linux基础,ARM开发板,软件配置等领域博主🌍快上🚘,一起学习,让我们成为一个强大的攻城狮!送给自己和读者的…...

[leetcode] 707 设计链表
707. 设L计链表 中等 902 相关企业 你可以选择使用单链表或者双链表,设计并实现自己的链表。 单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。 如果是双向链表,则还需…...

JIRA:项目管理的秘密武器
引言 在当今动态且快速变化的商业环境中,项目管理已经成为任何组织成功的关键因素。能够有效地管理项目,保证项目在设定的时间和预算内按照预期的质量完成,是每个项目经理的目标。为了实现这个目标,项目经理需要依赖强大的工具&a…...
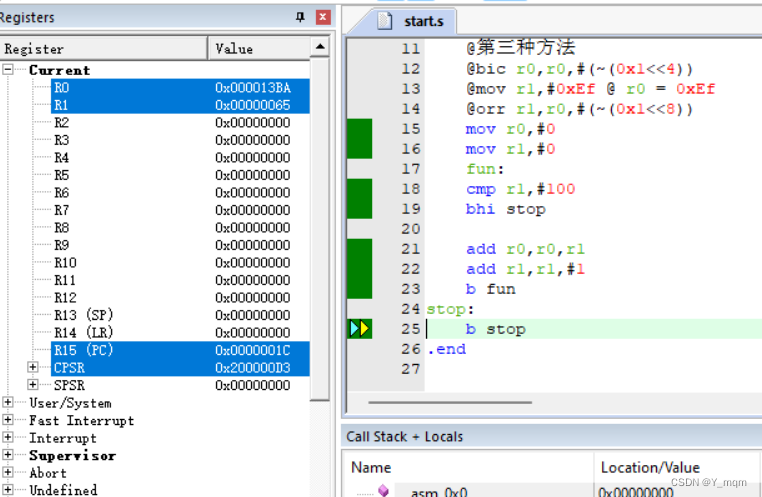
ARM 作业1
一、思维导图 二、 1. 2. .text 文本段 .globl _start 声明_start:mov r0,#0mov r1,#0fun:cmp r1,#100bhi stopadd r0,r0,r1add r1,r1,#1b fun stop:b stop .end...
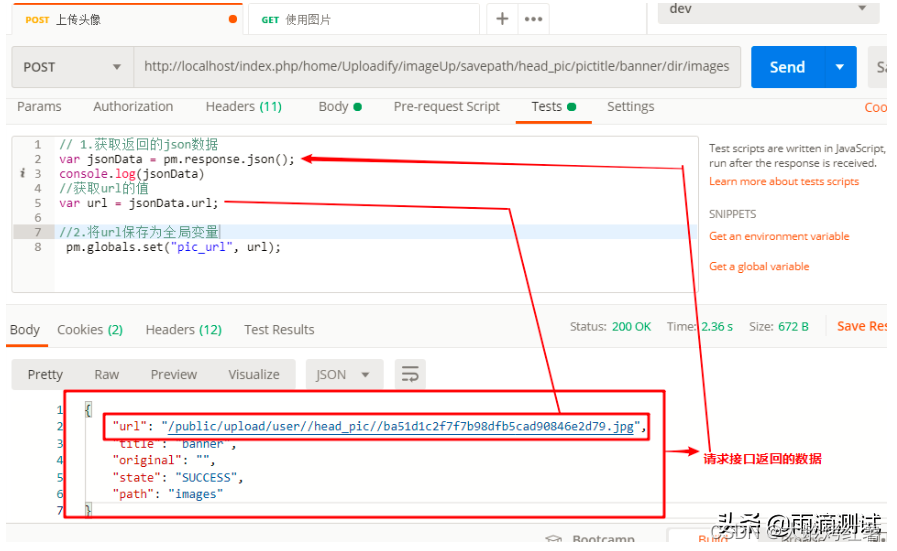
【解析postman工具的使用---基础篇】
postman前端请求详解 主界面1.常见类型的接口请求1.1 查询参数的接口请求1.1.1 什么是查询参数?1.1.2 postman如何请求 1.2 ❤表单类型的接口请求1.2.1 复习下http请求1.2.2❤ 什么是表单 1.3 上传文件的表单请求1.4❤ json类型的接口请求 2. 响应接口数据分析2.1 postman的响…...
Elasticsearch:如何在 Ubuntu 上安装多个节点的 Elasticsearch 集群 - 8.x
Elasticsearch 是一个强大且可扩展的搜索和分析引擎,可用于索引和搜索大量数据。 Elasticsearch 通常用于集群环境中,以提高性能、提供高可用性并实现数据冗余。 在本文中,我们将讨论如何在 Ubuntu 20.04 上安装和配置具有多节点集群的 Elast…...
记录win 7旗舰版 “VMware Alias Manager and Ticket Service‘(VGAuhService)启动失败。
记录win 7旗舰版 "VMware Alias Manager and Ticket Service’(VGAuhService)启动失败。 描述如图 https://learn.microsoft.com/zh-CN/cpp/windows/latest-supported-vc-redist?viewmsvc-140#visual-studio-2015-2017-2019-and-2022 安装对应版本的VC 库就可以解决问…...
git 开发环境配置
系统:Mac OS 1、下载git,官网已经推荐使用命令下载。 /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh) 2、验证git是否安装成功 git --version 3、配置本地git全局变量 git config --global user.n…...
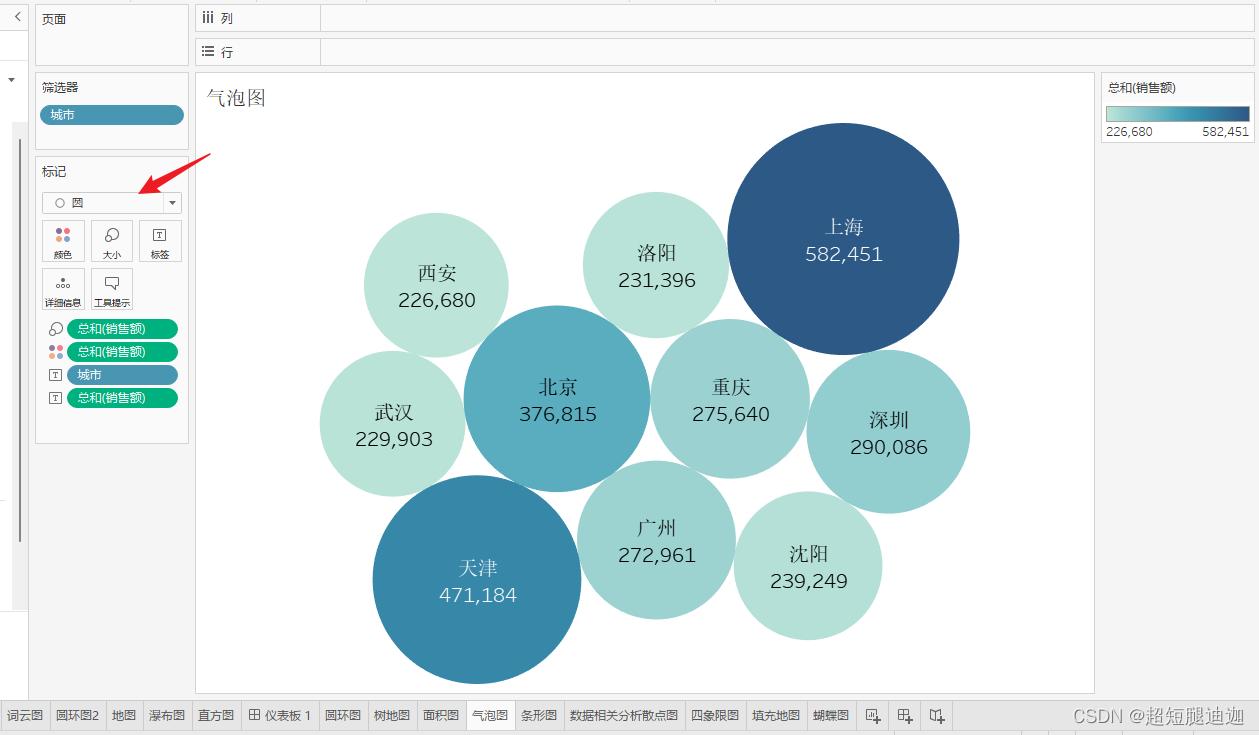
Tableau画图
目录 蝴蝶图 四象图 排序图 盒型图/散点图 圆环图 火柴图 直方图 瀑布图 地理图 面积图 树地图 面积图 条形图 词云图 双轴图 填充地图 tableau2023.2 须知 蝴蝶图 拉好数据之后 创建新字段正负销售额,并拖入第一个颜色标记卡 四象图 智能推荐 散…...
nginx上web服务的基本安全优化、服务性能优化、访问日志优化、目录资源优化和防盗链配置简介
一.基本安全优化 1.隐藏nginx软件版本信息 2.更改源码来隐藏软件名和版本 (1)修改第一个文件(核心头文件),在nginx安装目录下找到这个文件并修改 (2)第二个文件 (3)…...

himall3.0商城源码
目录 1 himall3.0商城源码 1.1 /// 获取待评价订单数量 1.2 /// 保存支付订单信息,生成支付订单 1.3 /// 取最近time分钟内的满足打印的订单数据 himall3.0商城源码 /// <summary>...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
