当前位置： 首页 > news >正文

RocketMQ消费者可以手动消费但无法主动消费问题，或生成者发送超时

news 2026/2/4 19:03:33

1.大多数是配置问题

在这里插入图片描述
修改rocketmq文件夹broker.conf

2.配置与集群IP或本地IPV4一样

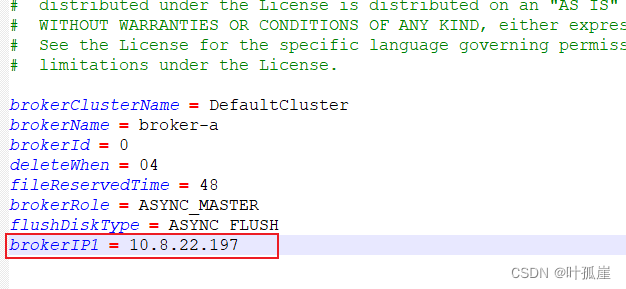
在这里插入图片描述
在这里插入图片描述

重启在这里插入图片描述

在RocketMQ独享实例中支持IPv4和IPv6双栈，主要是通过在网络层面上同时支持IPv4和IPv6协议栈来实现的。RocketMQ的Broker端、Namesrv端和客户端都需要支持IPv4和IPv6协议，以便能够同时监听IPv4和IPv6地址，并使用相应的协议栈进行通信。在Broker端，我们需要在配置文件中指定支持的网络类型为“IPv4 And IPv6”，来监听IPv4和IPv6地址。在客户端，我们需要在代码中显式指定连接的IPv4/IPv6地址信息，以确保能够使用正确的协议栈进行通信。

相关文章：

RocketMQ消费者可以手动消费但无法主动消费问题，或生成者发送超时

1.大多数是配置问题 修改rocketmq文件夹broker.conf 2.配置与集群IP或本地IPV4一样 重启 在RocketMQ独享实例中支持IPv4和IPv6双栈，主要是通过在网络层面上同时支持IPv4和IPv6协议栈来实现的。RocketMQ的Broker端、Namesrv端和客户端都需要支持IPv4和IPv6协议&…...

编程日记 2023/8/19 18:20:23

【数据库系统】--【2】DBMS架构

DBMS架构 01DBMS架构概述02 DBMS的物理架构03 DBMS的运行和数据架构DBMS的运行架构DBMS的数据架构PostgreSQL的体系结构RMDB的运行架构 04DBMS的逻辑和开发架构DBMS的层次结构DBMS的开发架构DBMS的代码架构 05小结 01DBMS架构概述 02 DBMS的物理架构 数据库系统的体系结构 数据…...

编程日记 2023/8/19 18:19:22

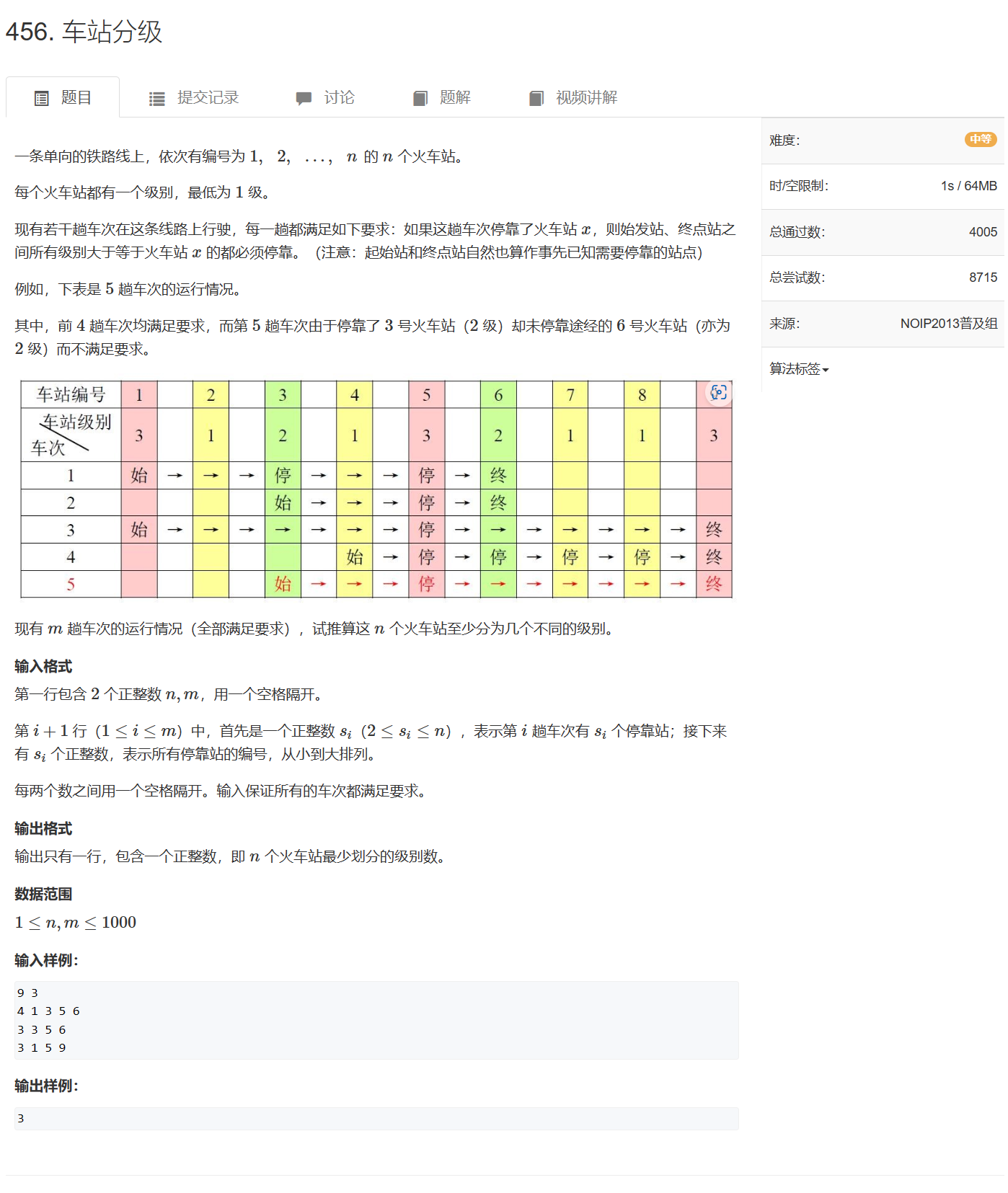
第三章 图论 No.13拓扑排序

文章目录 裸题：1191. 家谱树差分约束拓扑排序：1192. 奖金集合拓扑序：164. 可达性统计差分约束拓扑序：456. 车站分级 拓扑序和DAG有向无环图联系在一起，通常用于最短/长路的线性求解 裸题：1191. 家谱树 119…...

编程日记 2023/8/19 18:18:21

喜报 | 擎创再度入围IDC中国FinTech 50榜单

8月16日，2023年度“IDC中国FinTech 50”榜单正式揭晓，擎创科技继2022年入选该榜单后，再次以创新者姿态成功入选，并以技术赋能业务创新，成为中国金融科技领域创新与活力的重要贡献者。 “IDC中国FinTech 50”旨在评选出…...

编程日记 2023/8/19 18:17:19

【C++ 记忆站】引用

文章目录 一、引用概念二、引用特性1、引用在定义时必须初始化2、一个变量可以有多个引用3、引用一旦引用一个实体，再不能引用其他实体 三、常引用四、使用场景1、做参数1、输出型参数2、大对象传参 2、做返回值1、传值返回2、传引用返回 五、传值、传引用效率比较六…...

编程日记 2023/8/19 18:16:18

Hlang--用Python写个编程语言-变量的实现

文章目录 前言语法规则表示次幂实现变量实现优先级实现步骤解析关键字语法解析解释器总结前言 先前的话，我们终于是把我们整个架子搭起来了，这里重复一下我们的流程，那就是，首先，我们通过解析文本，然后呢遍历文本当中的我们定义的合法关键字，然后呢，把他们封装为一个T…...

编程日记 2023/8/19 18:15:17

多维时序 | MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测

多维时序 | MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测 目录 多维时序 | MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测基本介绍模型特点程序设计参考资料 基本介绍 本次运行测试环境MATLAB2021b，MATLAB实现PSO-CNN-BiLSTM多变量时间序列预测。代码说明&#xff1a…...

编程日记 2023/8/19 18:14:15

实现Java异步调用的高效方法

文章目录 为什么需要异步调用？Java中的异步编程方式1. 使用多线程2. 使用Java异步框架 异步调用的关键细节结论 🎉欢迎来到Java学习路线专栏~实现Java异步调用的高效方法 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页：IT陈寒的博…...

编程日记 2023/8/19 18:13:13

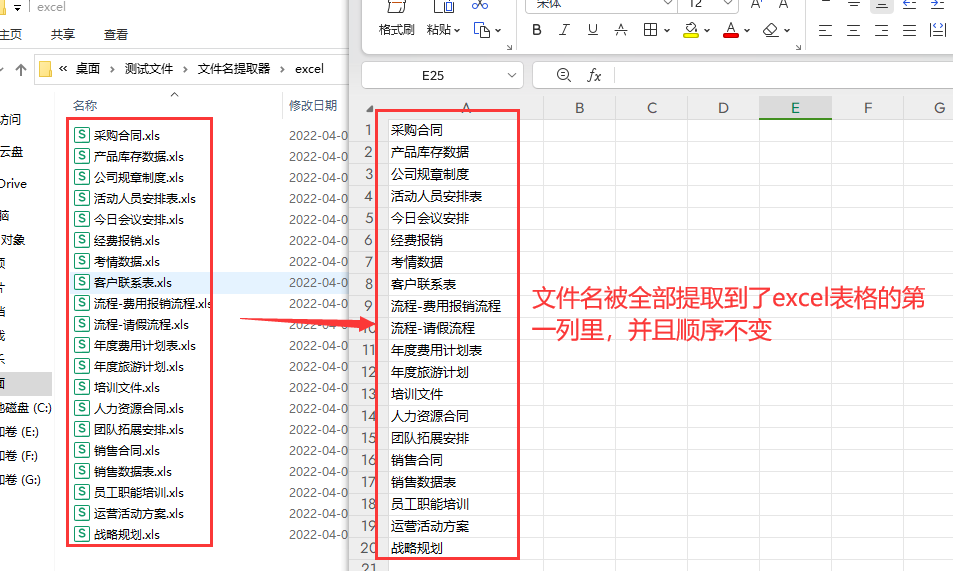
批量提取文件名到excel，详细的提取步骤

如何批量提取文件名到excel？我们的电脑中可能存储着数量非常多的电子文件，现在需要快速将这些文件的名称全部提取到Excel中。虽然少量数据可以通过复制粘贴的方式轻松完成，但是对于上万个数据而言，复制粘贴都是行不通的&#xff0…...

编程日记 2023/8/19 18:12:12

C#中的泛型约束可以用在以下几个地方？

1.泛型类型参数&#xff1a; 在定义泛型类型或泛型方法时&#xff0c;可以使用泛型约束来限制泛型类型参数的类型。这可以确保类型参数满足特定的条件&#xff0c;从而在编译时捕获错误并提供更安全和可靠的代码。 public class MyClass<T> where T : IComparable<T&…...

编程日记 2023/8/19 18:11:11

Linux Vm上部署Docker

创建ubutu虚拟机并远程连接&#xff0c; 参考 https://blog.csdn.net/m0_48468018/article/details/132267096 在终端中切换到root用户&#xff0c;并安装docker服务 2.1 切换到root用户 sudo su2.2 安装docker服务 , 参考 https://docs.docker.com/engine/install/ubuntu/ …...

编程日记 2023/8/19 18:10:10

ubuntu bind dns服务配置

sudo apt-get install bind9 内网搭建DNS服务器&#xff0c;大多数是解析纯内网地址使用。但是偶尔也需要解析外网的地址&#xff0c;所以我们可以配置DNS没有添加A记录的URL时&#xff0c;forward到外网DNS服务器或者内网的其他DNS服务器解析。 打开配置文件&#xff1a; sud…...

编程日记 2023/8/19 18:09:09

安卓的代码加固和其他安全问题

文章目录 安卓加固apk文件结构dex加固过程 其它安全问题 安卓加固 从App的加固技术来看:主流分为dex加密和so加密,目前来看保护dex文件更为重要,因为dex反编译后的java代码可读性更强。 android-ndk: Native Development Kit 官网解释&#xff1a;这套工具使您能在 Android 应…...

编程日记 2023/8/19 18:08:08

关于Linux Docker springboot jar 日志时间不正确 问题解决

使用Springboot项目的jar&#xff0c;制作了一个Docker镜像&#xff0c;启动该镜像后发现容器和容器中的Springboot 项目的日志时间不正确。 解决 查看容器时间命令为&#xff1a; docker exec 容器id date 1. 容器与宿主机同步时间 在启动镜像时候把操作系统的时间通过&q…...

编程日记 2023/8/19 18:07:06

提高批量爬虫工作效率

大家好&#xff01;作为一名专业的爬虫程序员&#xff0c;我今天要和大家分享一些关于提高批量爬虫工作效率的实用技巧。无论你是要批量采集图片、文本还是视频数据&#xff0c;这些经验都能帮助你在大规模数据采集中事半功倍。废话不多说&#xff0c;让我们开始吧&#xff01;…...

编程日记 2023/8/19 18:06:05

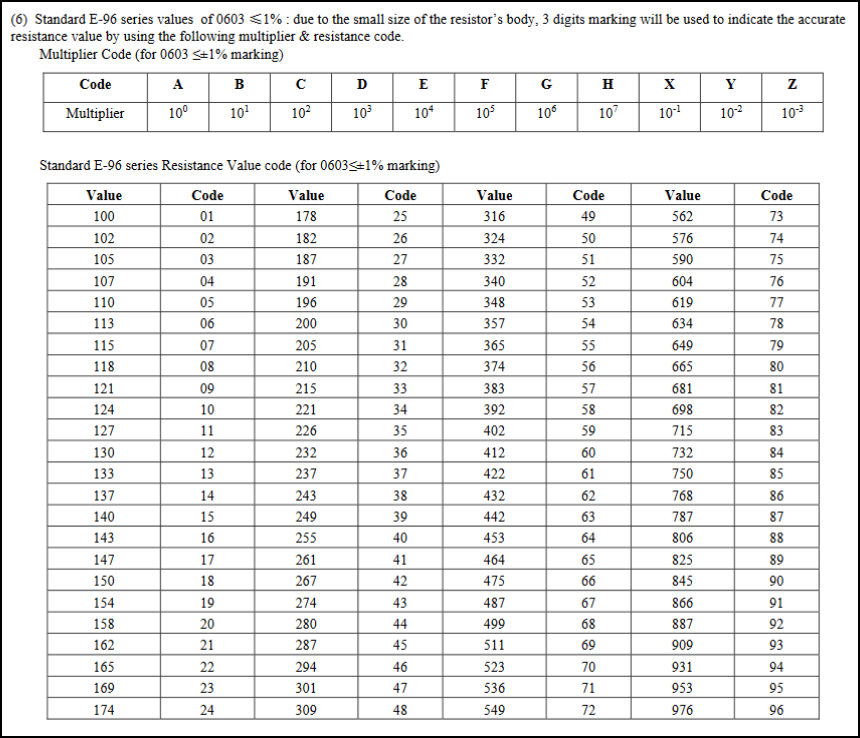
E96系列电阻阻值和代码、乘数对照表

1、为什么要用代码表示&#xff1f; 0805封装还可以简单易懂写下四位丝印&#xff0c;比如10K的1002&#xff0c;但0603的封装上面再想写下四位丝印就没空间了&#xff0c;就算写了也不容易看不清。 2、E96系列电阻阻值和代码、乘数对照表 下面是E96系列的对照表&#xff0c;…...

编程日记 2023/8/19 18:05:04

基于CentOS7.9安装部署docker（简洁版）

安装部署 1基于官方脚本安装&#xff08;不推荐 不能自行选择版本&#xff09; 官方文档&#xff1a;https://docs.docker.com/engine/install/centos/ 2 使用yum安装 阿里云文档&#xff1a;docker-ce镜像_docker-ce下载地址_docker-ce安装教程-阿里巴巴开源镜像站 # ste…...

编程日记 2023/8/19 18:04:01

MySQL常用练手题目

数据库表名和字段设计 1.学生表 Student(s_id,s_name,s_birth,s_sex) 学生编号,学生姓名, 出生年月,学生性别 2.课程表 Course(c_id,c_name,t_id) 课程编号, 课程名称, 教师编号 3.教师表 Teacher(t_id,t_name) 教师编号,教师姓名 4.成绩表 Score (s_id,c_id,s_score) 学生编号…...

编程日记 2023/8/19 18:02:58

Oracle字段长度不足位数补零

Oracle字段长度不足位数补零 有时候从数据库中取出的月份值是1&#xff0c;而不是01&#xff0c;该怎么办呢 SELECTLPAD( CODE_MONTH, 2, 0 ) FROMtb_cube_TY001 WHERECODE_BM_MEATYPE TY20 AND code_measure MYLX01 AND code_month <> ~ AND CODE_ENTITY 01A AND…...

编程日记 2023/8/19 18:01:57

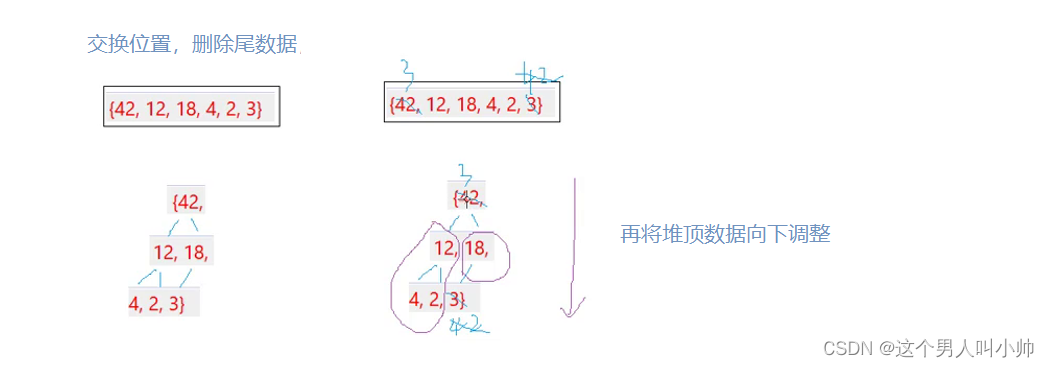
＜数据结构与算法＞二叉树堆的实现

目录 前言 一、树的概念及结构 1 树的概念 2 树的相关概念 二、二叉树的概念及结构 1.二叉树的概念 2. 特殊的二叉树 3. 二叉树的性质 4.二叉树的存储结构 三、二叉树的顺序结构及实现 1.堆的性质 2.堆的插入 3.堆的实现 堆的结构体 HeapInit 初始化 HeapPush 插入 HeapPop 删…...

编程日记 2023/8/19 18:00:56

JDK 17 新特性

#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持&#xff0c;不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的&#xff…...

编程新知 2026/1/29 5:34:29

【OSG学习笔记】Day 16: 骨骼动画与蒙皮（osgAnimation）

骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术&#xff0c;它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton)&#xff1a;由层级结构的骨头组成&#xff0c;类似于人体骨骼蒙皮 (Mesh Skinning)&#xff1a;将模型网格顶点绑定到骨骼上&#xff0c;使骨骼移动…...

编程新知 2026/2/1 5:42:50

CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云

目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

编程新知 2025/12/30 22:56:56

大数据学习（132）-HIve数据分析

​​​​&#x1f34b;&#x1f34b;大数据学习&#x1f34b;&#x1f34b; &#x1f525;系列专栏&#xff1a; &#x1f451;哲学语录: 用力所能及&#xff0c;改变世界。 &#x1f496;如果觉得博主的文章还不错的话&#xff0c;请点赞&#x1f44d;收藏⭐️留言&#x1f4…...

编程新知 2025/10/7 8:52:21

Typeerror: cannot read properties of undefined (reading ‘XXX‘)

最近需要在离线机器上运行软件&#xff0c;所以得把软件用docker打包起来&#xff0c;大部分功能都没问题&#xff0c;出了一个奇怪的事情。同样的代码&#xff0c;在本机上用vscode可以运行起来&#xff0c;但是打包之后在docker里出现了问题。使用的是dialog组件&#xff0c;…...

编程新知 2025/9/24 3:05:06

MySQL账号权限管理指南：安全创建账户与精细授权技巧

在MySQL数据库管理中&#xff0c;合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号&#xff1f; 最小权限原则&#xf…...

编程新知 2025/9/5 23:36:27

Python Ovito统计金刚石结构数量

大家好，我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构，但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法，可以持续统计各步的金刚石结构，具体代码如下： from ovito…...

编程新知 2026/1/26 5:39:08

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要&#xff1a; 近期&#xff0c;在使用较新版本的OpenSSH客户端连接老旧SSH服务器时&#xff0c;会遇到 "no matching key exchange method found"​, "n…...

编程新知 2025/9/29 4:00:38

云原生安全实战：API网关Kong的鉴权与限流详解

&#x1f525;「炎码工坊」技术弹药已装填&#xff01; 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关&#xff08;API Gateway&#xff09; API网关是微服务架构中的核心组件&#xff0c;负责统一管理所有API的流量入口。它像一座…...

编程新知 2026/2/1 6:24:16

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00