算法与数据结构(二十三)动态规划设计:最长递增子序列
注:此文只在个人总结 labuladong 动态规划框架,仅限于学习交流,版权归原作者所有;
也许有读者看了前文 动态规划详解,学会了动态规划的套路:找到了问题的「状态」,明确了 dp 数组/函数的含义,定义了 base case;但是不知道如何确定「选择」,也就是找不到状态转移的关系,依然写不出动态规划解法,怎么办?
不要担心,动态规划的难点本来就在于寻找正确的状态转移方程,本文就借助经典的「最长递增子序列问题」来讲一讲设计动态规划的通用技巧:数学归纳思想。
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是非常经典的一个算法问题,比较容易想到的是动态规划解法,时间复杂度 O(N^2),我们借这个问题来由浅入深讲解如何找状态转移方程,如何写出动态规划解法。比较难想到的是利用二分查找,时间复杂度是 O(NlogN),我们通过一种简单的纸牌游戏来辅助理解这种巧妙的解法。
力扣第 300 题「最长递增子序列open in new window」就是这个问题:
输入一个无序的整数数组,请你找到其中最长的严格递增子序列的长度,函数签名如下:
int lengthOfLIS(int[] nums);
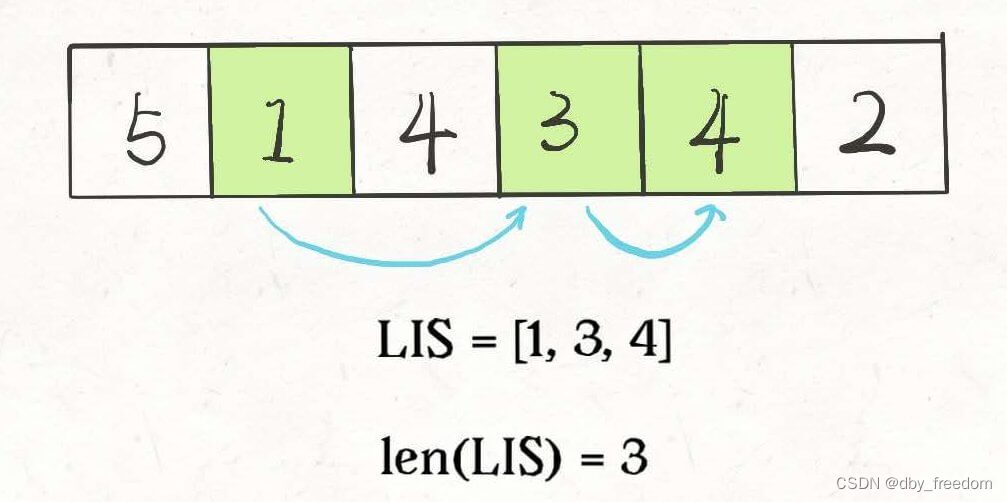
比如说输入 nums=[10,9,2,5,3,7,101,18],其中最长的递增子序列是 [2,3,7,101],所以算法的输出应该是 4。
注意「子序列」和「子串」这两个名词的区别,子串一定是连续的,而子序列不一定是连续的。下面先来设计动态规划算法解决这个问题。
一、动态规划解法
动态规划的核心设计思想是数学归纳法。
相信大家对数学归纳法都不陌生,高中就学过,而且思路很简单。比如我们想证明一个数学结论,那么我们先假设这个结论在 k < n 时成立,然后根据这个假设,想办法推导证明出 k = n 的时候此结论也成立。如果能够证明出来,那么就说明这个结论对于 k 等于任何数都成立。
类似的,我们设计动态规划算法,不是需要一个 dp 数组吗?我们可以假设 dp[0...i-1] 都已经被算出来了,然后问自己:怎么通过这些结果算出 dp[i]?
直接拿最长递增子序列这个问题举例你就明白了。不过,首先要定义清楚 dp 数组的含义,即 dp[i] 的值到底代表着什么?
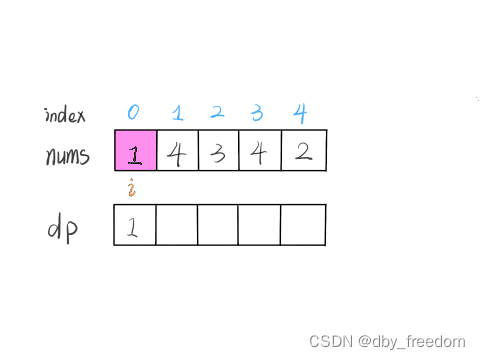
我们的定义是这样的:dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。
Info
为什么这样定义呢?这是解决子序列问题的一个套路,后文 动态规划之子序列问题解题模板 总结了几种常见套路。你读完本章所有的动态规划问题,就会发现dp数组的定义方法也就那几种。
根据这个定义,我们就可以推出 base case:dp[i] 初始值为 1,因为以 nums[i] 结尾的最长递增子序列起码要包含它自己。
举两个例子:
这个 GIF 展示了算法演进的过程:
根据这个定义,我们的最终结果(子序列的最大长度)应该是 dp 数组中的最大值。
int res = 0;
for (int i = 0; i < dp.length; i++) {res = Math.max(res, dp[i]);
}
return res;
读者也许会问,刚才的算法演进过程中每个 dp[i] 的结果是我们肉眼看出来的,我们应该怎么设计算法逻辑来正确计算每个 dp[i] 呢?
这就是动态规划的重头戏,如何设计算法逻辑进行状态转移,才能正确运行呢?这里需要使用数学归纳的思想:
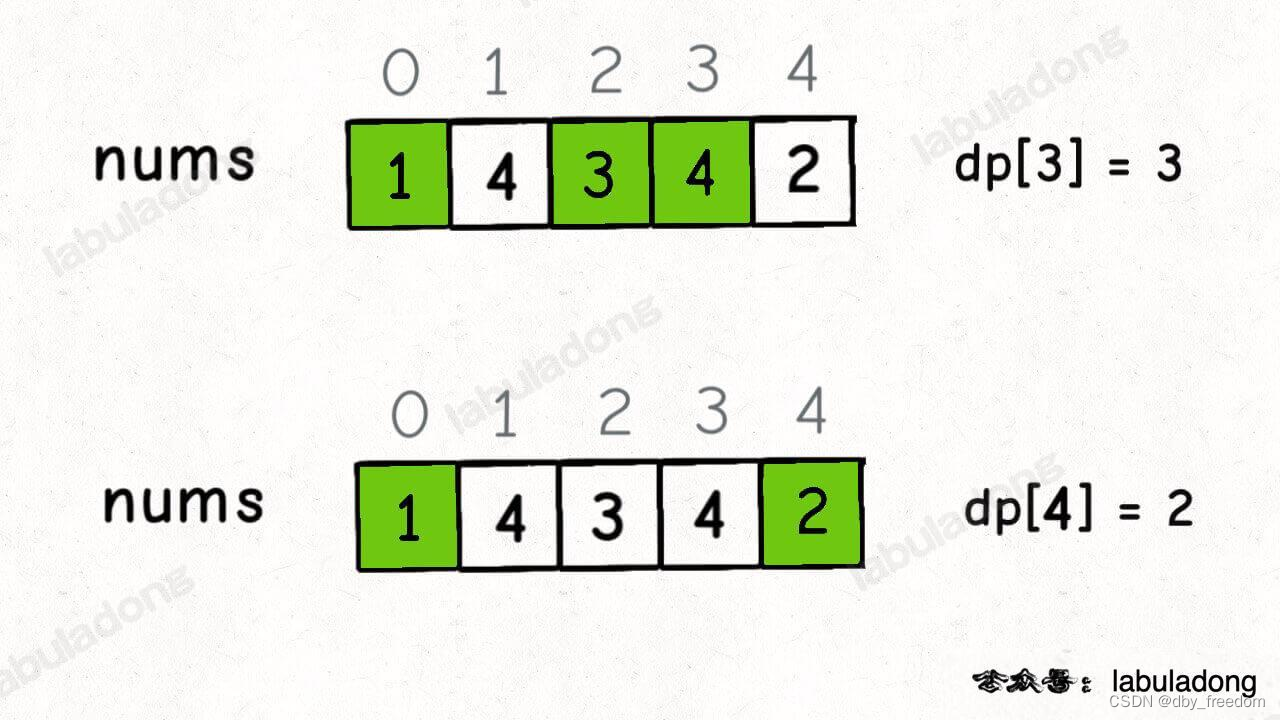
假设我们已经知道了 dp[0..4] 的所有结果,我们如何通过这些已知结果推出 dp[5] 呢?

根据刚才我们对 dp 数组的定义,现在想求 dp[5] 的值,也就是想求以 nums[5] 为结尾的最长递增子序列。
nums[5] = 3,既然是递增子序列,我们只要找到前面那些结尾比 3 小的子序列,然后把 3 接到这些子序列末尾,就可以形成一个新的递增子序列,而且这个新的子序列长度加一。
nums[5] 前面有哪些元素小于 nums[5]?这个好算,用 for 循环比较一波就能把这些元素找出来。
以这些元素为结尾的最长递增子序列的长度是多少?回顾一下我们对 dp 数组的定义,它记录的正是以每个元素为末尾的最长递增子序列的长度。
以我们举的例子来说,nums[0] 和 nums[4] 都是小于 nums[5] 的,然后对比 dp[0] 和 dp[4] 的值,我们让 nums[5] 和更长的递增子序列结合,得出 dp[5] = 3:
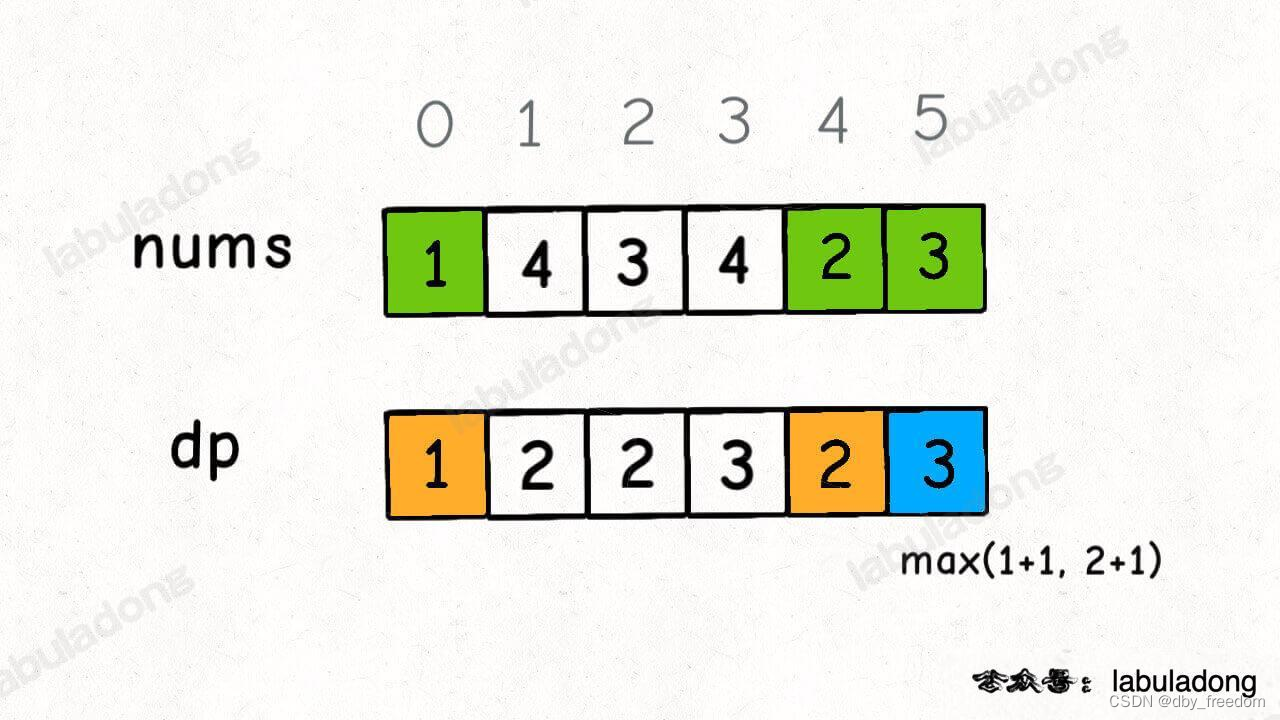
for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}
}
当 i = 5 时,这段代码的逻辑就可以算出 dp[5]。其实到这里,这道算法题我们就基本做完了。
读者也许会问,我们刚才只是算了 dp[5] 呀,dp[4], dp[3] 这些怎么算呢?类似数学归纳法,你已经可以算出 dp[5] 了,其他的就都可以算出来:
for (int i = 0; i < nums.length; i++) {for (int j = 0; j < i; j++) {// 寻找 nums[0..j-1] 中比 nums[i] 小的元素if (nums[i] > nums[j]) {// 把 nums[i] 接在后面,即可形成长度为 dp[j] + 1,// 且以 nums[i] 为结尾的递增子序列dp[i] = Math.max(dp[i], dp[j] + 1);}}
}
结合我们刚才说的 base case,下面我们看一下完整代码:
int lengthOfLIS(int[] nums) {// 定义:dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度int[] dp = new int[nums.length];// base case:dp 数组全都初始化为 1Arrays.fill(dp, 1);for (int i = 0; i < nums.length; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1);}}int res = 0;for (int i = 0; i < dp.length; i++) {res = Math.max(res, dp[i]);}return res;
}
至此,这道题就解决了,时间复杂度 O(N^2)。总结一下如何找到动态规划的状态转移关系:
1、明确 dp 数组的定义。这一步对于任何动态规划问题都很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
2、根据 dp 数组的定义,运用数学归纳法的思想,假设 dp[0...i-1] 都已知,想办法求出 dp[i],一旦这一步完成,整个题目基本就解决了。
但如果无法完成这一步,很可能就是 dp 数组的定义不够恰当,需要重新定义 dp 数组的含义;或者可能是 dp 数组存储的信息还不够,不足以推出下一步的答案,需要把 dp 数组扩大成二维数组甚至三维数组。
目前的解法是标准的动态规划,但对最长递增子序列问题来说,这个解法不是最优的,可能无法通过所有测试用例了,下面讲讲更高效的解法。
注:核心问题是 2 个:
- dp 数组的定义:最好能直接对应问题,如最长递增子序列中 dp 数组表示以 nums[i] 结尾的最长的递增最序列;
- dp 数组的推理:即知道
dp[0...i-1]都已知,如何求出dp[i];其中 dp 数组如何定义很重要!
二、拓展到二维
我们看一个经常出现在生活中的有趣问题,力扣第 354 题「俄罗斯套娃信封问题open in new window」,先看下题目:

这道题目其实是最长递增子序列的一个变种,因为每次合法的嵌套是大的套小的,相当于在二维平面中找一个最长递增的子序列,其长度就是最多能嵌套的信封个数。
前面说的标准 LIS 算法只能在一维数组中寻找最长子序列,而我们的信封是由 (w, h) 这样的二维数对形式表示的,如何把 LIS 算法运用过来呢?
读者也许会想,通过 w × h 计算面积,然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行,比如 1 × 10 大于 3 × 3,但是显然这样的两个信封是无法互相嵌套的。
这道题的解法比较巧妙:
先对宽度 w 进行升序排序,如果遇到 w 相同的情况,则按照高度 h 降序排序;之后把所有的 h 作为一个数组,在这个数组上计算 LIS 的长度就是答案。
画个图理解一下,先对这些数对进行排序:

然后在 h 上寻找最长递增子序列,这个子序列就是最优的嵌套方案:

那么为什么这样就可以找到可以互相嵌套的信封序列呢?稍微思考一下就明白了:
首先,对宽度 w 从小到大排序,确保了 w 这个维度可以互相嵌套,所以我们只需要专注高度 h 这个维度能够互相嵌套即可。
其次,两个 w 相同的信封不能相互包含,所以对于宽度 w 相同的信封,对高度 h 进行降序排序,保证二维 LIS 中不存在多个 w 相同的信封(因为题目说了长宽相同也无法嵌套)。
下面看解法代码:
// envelopes = [[w, h], [w, h]...]
public int maxEnvelopes(int[][] envelopes) {int n = envelopes.length;// 按宽度升序排列,如果宽度一样,则按高度降序排列Arrays.sort(envelopes, new Comparator<int[]>() {public int compare(int[] a, int[] b) {return a[0] == b[0] ? b[1] - a[1] : a[0] - b[0];}});// 对高度数组寻找 LISint[] height = new int[n];for (int i = 0; i < n; i++)height[i] = envelopes[i][1];return lengthOfLIS(height);
}int lengthOfLIS(int[] nums) {// 见前文
}
为了清晰,我将代码分为了两个函数, 你也可以合并,这样可以节省下 height 数组的空间。
此处放上 Leetcode 官方答案,个人觉着解释的更清晰一些:
根据题目的要求, 如果我们选择了 k k k 个信封, 它们的的宽度依次为 w 0 , w 1 , ⋯ , w k − 1 w_0, w_1, \cdots, w_{k-1} w0,w1,⋯,wk−1, 高度依次为
h 0 , h 1 , ⋯ , h k − 1 h_0, h_1, \cdots, h_{k-1} h0,h1,⋯,hk−1, 那么需要满足: { w 0 < w 1 < ⋯ < w k − 1 h 0 < h 1 < ⋯ < h k − 1 \left\{\begin{array}{l} w_0<w_1<\cdots<w_{k-1} \\ h_0<h_1<\cdots<h_{k-1} \end{array}\right. {w0<w1<⋯<wk−1h0<h1<⋯<hk−1
同时控制 w w w 和 h h h 两个维度并不是那么容易, 因此我们考虑固定一个维度, 再在另一个维度上进行选 择。例如, 我们固定 w w w
维度, 那么我们将数组 envelopes 中的所有信封按照 w w w 升序排序。这样一 来,
我们只要按照信封在数组中的出现顺序依次进行选取, 就一定保证满足: w 0 ≤ w 1 ≤ ⋯ ≤ w k − 1 w_0 \leq w_1 \leq \cdots \leq w_{k-1} w0≤w1≤⋯≤wk−1 了。然而小于等于 ≤ \leq ≤ 和小于 < < < 还是有区别的,但我们不妨首先考虑一个简化版本的问题:
如果我们保证所有信封的 w 值互不相同, 那么我们可以设计出一种得到答案的方法吗? 在 w w w 值互不相同的前提下,小于等于 ≤ \leq ≤
和小于 < < < 是等价的,那么我们在排序后,就可以完全忽略 w w w 维度, 只需要考虑 h h h 维度了。此时, 我们需要解决的问题即为:
给定一个序列, 我们需要找到一个最长的子序列, 使得这个子序列中的元素严格单调递增, 即上面 要求的:
h 0 < h 1 < ⋯ < h k − 1 > h_0<h_1<\cdots<h_{k-1}> h0<h1<⋯<hk−1> 那么这个问题就是经典的「最长严格递增子序列」问题了, 读者可以参考力扣平台的 300 . 最长递增 子序列 及其 官方题解。最长严格递增子序列的详细解决方法属于解决本题的前置知识点, 不是本文分析的重点, 因此这里不再赘述,会在方法一和方法二中简单提及。 当我们解决了简化版本的问题之后, 我们来想一想使用上面的方法解决原问题, 会产生什么错误。当 w w w
值相同时,如果我们不规定 h h h 值的排序顺序,那么可能会有如下的情况: 排完序的结果为 [ ( w , h ) ] = [ ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) ] [(w,h)]=[(1,1),(1,2),(1,3),(1,4)] [(w,h)]=[(1,1),(1,2),(1,3),(1,4)], 由于这些信封的 w w w 值都相同, 不存在一个 信封可以装下另一个信封, 那么我们只能在其中选择 1 个信封。然而如果我们完全忽略 w w w 维度, 剩下的 h h h 维度为 [ 1 , 2 , 3 , 4 ] [1,2,3,4] [1,2,3,4],
这是一个严格递增的序列, 那么我们就可以选择所有的 4 个信封了, 这就产生了错误。 因此,我们必须要保证对于每一种 w w w 值,我们最多只能选择 1 个信封。 我们可以将 h h h 值作为排序的第二关键字进行降序排序, 这样一来, 对于每一种 w w w 值, 其对应的信封 在排序后的数组中是按照 h h h 值递减的顺序出现的, 那么这些 h h h 值不可能组成长度超过 1 的严格递增的序列,这就从根本上杜绝了错误的出现。 因此我们就可以得到解决本题需要的方法:
- 首先我们将所有的信封按照 w w w 值第一关键字升序、 h h h 值第二关键字降序进行排序;
- 随后我们就可以忽略 w w w 维度, 求出 h h h 维度的最长严格递增子序列, 其长度即为答案。 下面简单提及两种计算最长严格递增子序列的方法, 更详细的请参考上文提到的题目以及对应的官方 题解。
最后赋上个人题解:
def maxEnvelopes(self, envelopes):""":type envelopes: List[List[int]]:rtype: int"""envelopes.sort(key = lambda x: (x[0], -x[1]))# heigth = [1] * len(envelopes)# for i in range(len(envelopes)):# heigth[i] = envelopes[i][1]# return self.lcs(heigth)return self.lcsPro(envelopes)def lcs(self, heigth):if len(heigth) <= 1:return 1dp = [1] * len(heigth)for i in range(len(heigth)):for j in range(i):if heigth[i] > heigth[j]:dp[i] = max(dp[i], dp[j] + 1)return max(dp)def lcsPro(self, envelopes):if len(envelopes) <= 1:return 1dp = [1] * len(envelopes)for i in range(len(envelopes)):for j in range(i):if envelopes[i][1] > envelopes[j][1]:dp[i] = max(dp[i], dp[j] + 1)return max(dp) ```
三、参考文献
[1] 动态规划设计:最长递增子序列
[2] Leetcode 官方题解
相关文章:

算法与数据结构(二十三)动态规划设计:最长递增子序列
注:此文只在个人总结 labuladong 动态规划框架,仅限于学习交流,版权归原作者所有; 也许有读者看了前文 动态规划详解,学会了动态规划的套路:找到了问题的「状态」,明确了 dp 数组/函数的含义&a…...
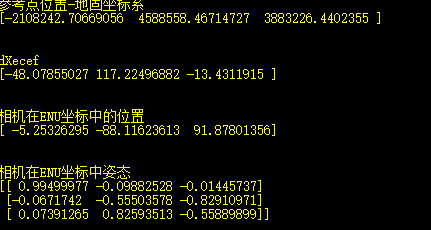
相机的位姿在地固坐标系ECEF和ENU坐标系的转换
在地球科学和导航领域,通常使用地心地固坐标系(ECEF,Earth-Centered, Earth-Fixed)和东北天坐标系(ENU,East-North-Up)来描述地球上的位置和姿态。如下图所示: 地心地固坐标ecef和…...

RFID技术助力汽车零配件装配产线,提升效率与准确性
随着科技的不断发展,越来越多的自动化设备被应用到汽车零配件装配产线中。其中,射频识别(Radio Frequency Identification,简称RFID)技术凭借其独特的优势,已经成为了这一领域的重要技术之一。本文将介绍RF…...

应用高分辨率 GAN 对扰动文档图像去扭曲的深度Python实践
1. 引言 随着技术的不断发展,图像处理在各种场景中的应用也变得越来越广泛。高分辨率 GAN (Generative Adversarial Network) 是近年来图像处理领域的热点技术,它能够生成极高分辨率的图像,与此同时,它也可以用于各种修复和增强任…...
)
【BASH】回顾与知识点梳理(二十六)
【BASH】回顾与知识点梳理 二十六 二十六. 二十一至二十五章知识点总结及练习26.1 总结26.2 模拟26.3 简答题 该系列目录 --> 【BASH】回顾与知识点梳理(目录) 二十六. 二十一至二十五章知识点总结及练习 26.1 总结 Linux 操作系统上面,…...

React下载文件的两种方式
React下载文件的两种方式 - 代码先锋网 不知道有用没用看着挺整齐 没试过 1、GET类型下载 download url > {const eleLink document.createElement(a);eleLink.style.display none;// eleLink.target "_blank"eleLink.href url;// eleLink.href record;d…...

python入门知识:分支结构
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 1.内容导图 👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~ python资料、视频教程、代码、插件安装教程等我都准备好了,直接在文末名片自…...

DNS协议及其工作原理
DNS是域名系统(Domain Name System)的缩写,它是一种用于将域名转换为IP地址的分布式数据库系统。它是因特网的基石,能够使人们通过域名方便地访问互联网,而无需记住复杂的IP地址。 DNS的历史可以追溯到1983年…...

调用被fishhook的原函数
OC类如果通过runtime被hook了,可以通过逆序遍历方法列表的方式调用原方法。 那系统库的C函数被fish hook了该怎么办呢? 原理和OC类异曲同工,即通过系统函数dlopen()获取动态库,以动态库为参数通过系统函数dlsym()即可获取目标系统…...
java语言B/S架构云HIS医院信息系统源码【springboot】
医院云HIS全称为基于云计算的医疗卫生信息系统( Cloud- Based Healthcare Information System),是运用云计算、大数据、物联网等新兴信息技术,按照现代医疗卫生管理要求,在一定区域范围内以数字化形式提供医疗卫生行业数据收集、存储、传递、…...

go文件基本操作
一、文件读操作 文件内容如下: 水陆草木之花,可爱者甚蕃。 晋陶渊明独爱菊。自李唐来,世人甚爱牡丹。 予独爱莲之出淤泥而不染,濯清涟而不妖,中通外直,不蔓不枝,香远益清,亭亭净植…...

每日一学——应用层
以下是一份关于应用层协议的学习资料: DNS (Domain Name System):DNS是互联网上最常用的应用层协议之一,它将域名转换为对应的IP地址。你可以了解DNS的工作原理、域名解析过程和常见的DNS记录类型。 DHCP (Dynamic Host Configuration Proto…...

blender的快捷键记录
按键作用备注R旋转物体移动、旋转或缩放物体时,按下X、Y或Z键:按X、Y或Z轴方向移动、旋转或缩放S缩放物体G移动物体TAB键切换为编辑模式CTRL A弹出应用菜单物体模式旋转缩放后应用旋转与缩放,再进入编辑模式SHIFT 鼠标右键移动游标位置SHIF…...
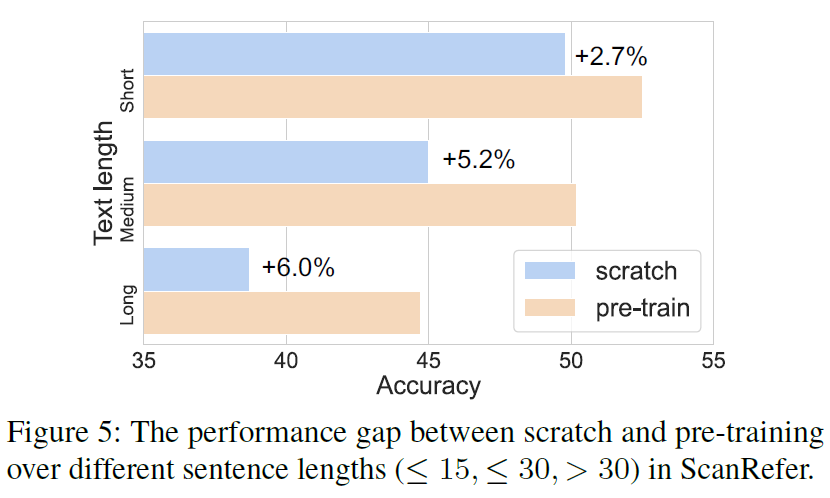
3D- vista:预训练的3D视觉和文本对齐Transformer
论文:https://arxiv.org/abs/2308.04352 代码: GitHub - 3d-vista/3D-VisTA: Official implementation of ICCV 2023 paper "3D-VisTA: Pre-trained Transformer for 3D Vision and Text Alignment" 摘要 三维视觉语言基础(3D- vl)是一个新兴领域&…...
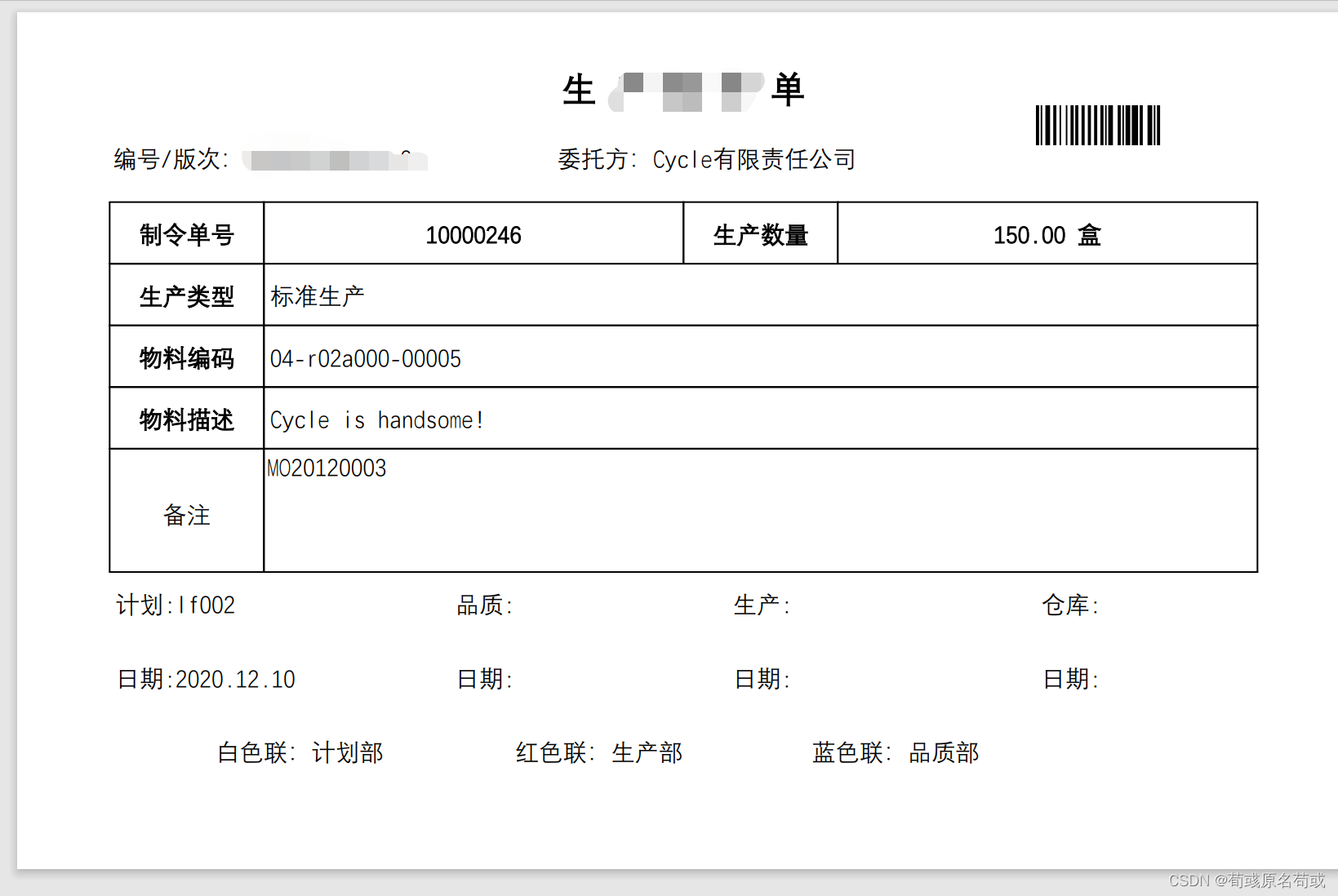
SAP ABAP 直接把内表转换成PDF格式(smartform的打印函数输出OTF格式数据)
直接上代码: REPORT zcycle055.DATA: lt_tab TYPE TABLE OF zpps001. DATA: ls_tab TYPE zpps001.ls_tab-werks 1001. ls_tab-gamng 150.00. ls_tab-gstrp 20201202. ls_tab-aufnr 000010000246. ls_tab-auart 标准生产. ls_tab-gltrp 20201205. ls_tab-matn…...
侯捷 C++ part2 兼谈对象模型笔记——7 reference、const、new/delete
7 reference、const、new/delete 7.1 reference x 是整数,占4字节;p 是指针占4字节(32位);r 代表x,那么r也是整数,占4字节 int x 0; int* p &x; // 地址和指针是互通的 int& r x;…...

C++学习笔记总结练习:primer 学习日志
文章目录 针对自己的引言学习内容c语言基础知识1.为什么要声明变量2.cout ,cin3.c 不容许一个函数定义嵌套到另一个函数的定义中。4.编译指令using5.c基本类型长度6.在定义常量时尽可能使用const 关键字而不用#define9.前缀递增符与后缀递增符的区别10.c中的cctype库11.c 中的s…...
发布一个开源的新闻api(整理后就开源)
目录 说明: 基础说明 其他说明: 通用接口: 登录: 注册: 更改密码(需要token) 更换头像(需要token) 获取用户列表(需要token): 上传文件(5000端口): 获取文件(5000端口)源码文件,db文件均不能获取: 验证token(需要token): 获取系统时间: 文件…...

3d max省时插件CG MAGIC功能中的材质参数可一键优化!
渲染的最终结果就是为了让渲染效果更加真实的体现。 对于一些操作上,可能还是费些时间,VRay可以说是在给材质做加法的路上越走越远,透明度、凹凸、反射等等参数细节越做越多。 对于材质参数调节的重要性大家都心里有数的。 VRay材质系统的每…...

什么是变量提升(hoisting)?它在JavaScript中是如何工作的?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 变量提升(Hoisting)⭐ 变量提升的示例:⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅&…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
