深入探讨lowess算法:纯C++实现与局部加权多项式回归的数据平滑技术
引言
在统计学和数据科学中,有时我们面对的数据是嘈杂的、充满噪声的。为了更好地揭示数据的潜在趋势和结构,数据平滑技术成为了一个重要工具。lowess或称为局部加权多项式回归是其中的一种流行方法,它对每一个点给予一个权重,根据其到给定点的距离进行加权。
本文将重点探讨lowess算法的核心思想,并提供其纯C++的实现方法。我们还将对算法进行一些基本的优化和改进,使其在大数据场景下表现得更加出色。
1. lowess算法简介
局部加权散点平滑技术(LOWESS)是一种非参数方法,用于拟合数据系列,特别是当需要捕获数据的非线性趋势时。不同于传统的线性或多项式回归,LOWESS考虑到每个数据点的局部特性,使其能够更加敏感地捕获数据的变化。
2. 算法原理
lowess的基本思想是对数据集中的每一个点,都用其邻近的数据点进行多项式回归。这里的"邻近"是通过权重函数定义的,距离越近的点有更高的权重。
具体算法步骤如下:
-
对于数据集中的每一个点
x_i:- 计算其与其他所有点的距离。
- 基于距离,为每个点分配一个权重。
- 使用加权的多项式回归拟合这些点。
- 计算拟合多项式在
x_i处的值。
-
重复以上步骤,直到收敛或达到预定的迭代次数。
3. 纯C++的实现
首先,让我们来定义数据结构和必要的函数:
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>// 定义数据点结构
struct Point {double x;double y;
};// 计算两点间的距离
double distance(const Point& p1, const Point& p2) {return std::abs(p1.x - p2.x);
}// 权重函数
double weightFunction(double dist, double bandwidth) {return std::exp(-std::pow(dist/bandwidth, 2));
}// ...这部分代码首先定义了一个表示数据点的结构,并为此定义了一个计算两点间距离的函数和一个计算权重的函数。
具体过程请下载完整项目。
4. 加权多项式回归
对于每个数据点,我们需要进行加权多项式回归。这里我们选择一个简单的线性多项式回归作为例子。具体地说,我们尝试拟合以下形式的模型:
y=ax+by = ax + by=ax+b
其中,权重在回归中起到关键作用。
// 拟合加权线性回归的函数
void weightedLinearRegression(const std::vector<Point>& points, const std::vector<double>& weights, double& a, double& b) {double Wxy = 0, Wx = 0, Wy = 0, Wxx = 0, W = 0;for (size_t i = 0; i < points.size(); i++) {double x = points[i].x;double y = points[i].y;double w = weights[i];Wxy += w * x * y;Wx += w * x;Wy += w * y;Wxx += w * x * x;W += w;}a = (W * Wxy - Wx * Wy) / (W * Wxx - Wx * Wx);b = (Wy - a * Wx) / W;
}// ...5. LOWESS算法核心
有了上面的工具函数,我们可以继续编写LOWESS的核心函数。
std::vector<double> lowess(const std::vector<Point>& points, double bandwidth, int iterations) {std::vector<double> smoothedY(points.size());for (int iter = 0; iter < iterations; iter++) {for (size_t i = 0; i < points.size(); i++) {std::vector<double> weights(points.size());for (size_t j = 0; j < points.size(); j++) {weights[j] = weightFunction(distance(points[i], points[j]), bandwidth);}double a, b;weightedLinearRegression(points, weights, a, b);smoothedY[i] = a * points[i].x + b;}}return smoothedY;
}// ...在这部分代码中,我们首先为每个点计算了权重,然后使用这些权重进行加权线性回归。这个过程会迭代多次,直到数据平滑到满意的程度。
6. 总结和优化
纯C++的LOWESS实现提供了一个高效且直观的方式来平滑数据。然而,本文提供的方法仅是最基础的版本。在实际应用中,可能需要进一步优化以处理大规模数据集。
-
并行化:考虑到每个点的平滑操作是独立的,我们可以使用C++的多线程库来并行处理数据,从而大大提高算法的速度。
-
选择性平滑:对于大规模的数据集,我们可以考虑只对数据的子集进行平滑,而不是整个数据集。
-
更高阶的多项式回归:在某些情况下,线性多项式可能不足以捕捉数据的复杂性。此时,可以考虑二次或更高阶的多项式回归。
7. 如何使用纯C++ LOWESS算法
要使用上述的LOWESS实现,首先需要收集并整理你的数据。将数据组织成Point结构的列表,并为其提供一个合适的带宽值和迭代次数。
int main() {std::vector<Point> data = { /*... your data here ...*/ };// 运行LOWESS算法double bandwidth = 1.0; // 选择合适的带宽值int iterations = 3;std::vector<double> smoothedValues = lowess(data, bandwidth, iterations);// 输出平滑后的数据for (size_t i = 0; i < data.size(); i++) {std::cout << data[i].x << ", " << smoothedValues[i] << std::endl;}return 0;
}
8. 优势与限制
LOWESS算法有其独特的优势:
- 非参数性:这意味着它不需要预先假定数据符合某种特定的形式或分布。
- 局部性:它能够敏感地捕捉到数据的局部特点和非线性趋势。
然而,LOWESS也有其局限性:
- 计算复杂度:对于大数据集,算法可能会非常耗时。
- 参数选择:带宽和迭代次数的选择对结果影响很大,但往往需要多次尝试来确定最佳参数。
9. 未来方向和其他技术
尽管LOWESS是一个强大的数据平滑工具,但在数据科学的快速发展中,还有其他许多方法和技术值得探索,例如深度学习的不同变体、高斯过程回归等。这些方法在处理特定类型的数据或问题时可能更有优势。
此外,使用纯C++实现LOWESS仅是众多可能的实现方法之一。Python、R等语言也有LOWESS的实现,而这些语言通常带有更为强大的数据处理和可视化工具。
结束语
LOWESS算法为数据科学家和研究者提供了一种灵活、直观的方式来观察和分析数据的底层结构。本文的纯C++实现为读者提供了一个入门的机会,但真正的深入理解和高效应用还需要大量的实践和经验积累。
最后,如有需要获取更多的细节或优化版本的代码,具体过程请下载完整项目。
希望这篇文章能为你提供关于LOWESS算法和其C++实现的有用信息。随着技术的发展,总有新的方法和工具出现,但基本的算法和思想往往有其持久的价值。
相关文章:

深入探讨lowess算法:纯C++实现与局部加权多项式回归的数据平滑技术
引言 在统计学和数据科学中,有时我们面对的数据是嘈杂的、充满噪声的。为了更好地揭示数据的潜在趋势和结构,数据平滑技术成为了一个重要工具。lowess或称为局部加权多项式回归是其中的一种流行方法,它对每一个点给予一个权重,根…...
 Groth16的可塑性)
Sui安全篇|详解零知识证明 (ZKP) Groth16的可塑性
Sui Move允许用户使用Groth16进行高效验证任何非确定性多项式时间(Non-deterministic Polynomial time ,NP)状态。Groth16是一种高效且广泛使用的零知识简洁非交互知识证明(Zero-Knowledge Succinct Non-interactive Argument of …...

记录--webpack和vite原理
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 前言 每次用vite创建项目秒建好,前几天用vue-cli创建了一个项目,足足等了我一分钟,那为什么用 vite 比 webpack 要快呢,这篇文章带你梳理清楚它们的原理…...

Windows系统中使用bat脚本启动git bash 并运行指定命令 - 懒人一键git更新
目标 双击"autoGitPull.bat",自动打开git bash,并cd到项目,逐个git pull,保留git bash窗口展示进度。 脚本 start "" "D:\Program Files\Git\git-bash.exe" -c "echo autoGitPull &&…...

elementui form组件出现英文提示
今天让解决一个bug,是表单组件提示词会出现英文。 问题情景如下: 有时会出现中文,有时会出现英文。 解决方法: 经查看,代码采用的是elementui的form组件,在el-form-item中使用了required属性,同…...

使用windows Api简单验证ISO9660文件格式,以及装载和卸载镜像文件
使用IIsoImageManager接口简单验证ISO镜像文件正确性,使用AttachVirtualDisk装载ISO镜像文件,和使用DetachVirtualDisk卸载,(只支持windows 8及以上系统) 导读 IIsoImageManager 验证ISO文件正确性AttachVirtualDisk 装载镜像文件DetachVirtualDisk 卸载镜像文件其他相关函…...

iPhone 15受益:骁龙8 Gen 3可能缺席部分安卓旗舰机
明年一批领先的安卓手机的性能可能与今年的机型非常相似。硅成本的上涨可能是原因。 你可以想象,2024年许多最好的手机都会在Snapdragon 8 Gen 3上运行,这是高通公司针对移动设备的顶级芯片系统的更新,尚未宣布。然而,来自中国的…...
理解持续测试,才算理解DevOps
软件产品的成功与否,在很大程度上取决于对市场需求的及时把控,采用DevOps可以加快产品交付速度,改善用户体验,从而有助于保持领先于竞争对手的优势。 作为敏捷开发方法论的一种扩展,DevOps强调开发、测试和运维不同团…...

使用OpenCV与深度学习从视频和图像中精准识别人脸: Python实践指南
第一部分: 引言与背景 人脸识别已经成为了当代技术领域中最热门和广泛应用的话题之一。从智能手机的解锁功能到机场的安全检查,人脸识别技术无处不在。在这篇文章中,我们将使用Python中的OpenCV库和深度学习模型,深入探讨如何从视频和图像中…...

面试之快速学习C++11-完美转发,nullptr, shared_ptr,unique_ptr,weak_ptr,shared_from_this
完美转发及其实现 函数模版可以将自己的参数完美地转发给内部调用的其他函数。所谓完美,即不仅能准确地转发参数的值,还能保证被转发参数的左右值属性不变引用折叠:如果任一引用为左值引用,则结果为左值引用,否则为右…...
android resoure资源图片颜色值错乱
最近androidstudio开发,添加一些颜色值或者drawable资源文件时,运行app,颜色值或者图片对应不上,暂时找不到原因,望告知。 暂时解决方法:...

leetcode第 357/358 场周赛
2817. 限制条件下元素之间的最小绝对差 可能别人有更好的解法,我这写法是不断往线段树中插入数值,每次先插入nums[i-x],然后搜索(1到i)中的最大值和(i到max)中的最小值去更新ans。 class Solution { public:struct node{int mx,…...
Jmeter 分布式性能测试避坑指南
在做后端服务器性能测试中,我们会经常听到分布式。那你,是否了解分布式呢?今天,我们就来给大家讲讲,在企业实战中,如何使用分布式进行性能测试,实战过程中,又有哪些地方要特别注意&a…...

基于SpringCloud的会议室预约系统Java基于微服务的会议室报修系统【源码+lw】
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、微信小程序、Python、Android、大数据等,大家有这一块的问题可以一起交流! 💕💕…...

idea设置忽略大小写
1.点击file 2.点击settings 3.点击Editor选项 4.点击general选项 5.点击code completion 6.点击左上角match case...
re学习(35)攻防世界-no-strings-attached(动调)
参考文章:re学习笔记(28)攻防世界-re-no-strings-attached_Forgo7ten的博客-CSDN博客 攻防世界逆向入门题之no-strings-attached_攻防世界 no-strings-attached_沐一 林的博客-CSDN博客 本人题解: 扔入Exepeinfo中查壳和其他信息…...

STM32 F103C8T6学习笔记8:0.96寸单色OLED显示屏显示字符
使用STM32F103 C8T6 驱动0.96寸单色OLED显示屏: OLED显示屏的驱动,在设计开发中OLED显示屏十分常见,因此今日学习一下。一篇文章从程序到显示都讲通。 文章提供源码、原理解释、测试工程下载,测试效果图展示。 目录 OLED驱动原理—IIC通信…...
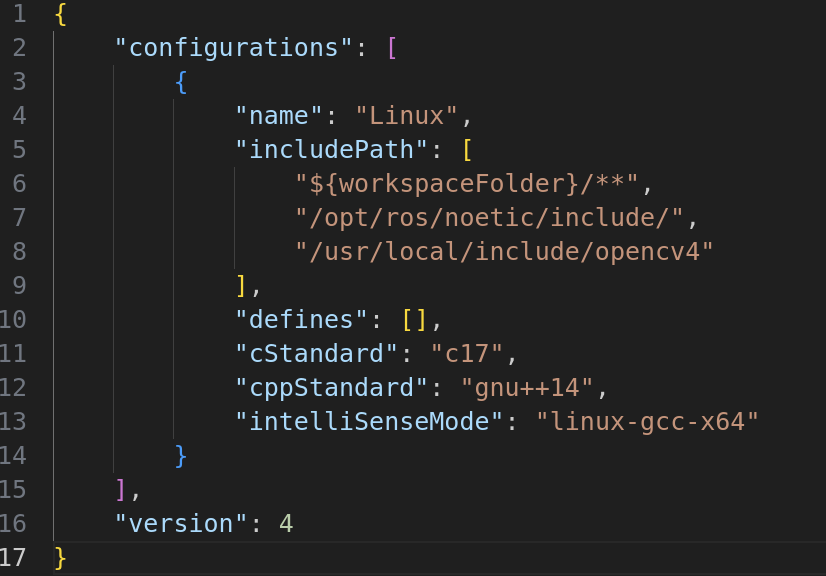
vscode的配置和使用
1.侧边栏调整大小 放大:View -> Appearance -> Zoom in(快捷键Ctrl ) 缩小:View -> Appearance -> Zoom out(快捷键Ctrl -) 侧边栏字体调整到合适大小后,可以按下一步调整代码区…...

SpringBoot统⼀功能处理
前言🍭 ❤️❤️❤️SSM专栏更新中,各位大佬觉得写得不错,支持一下,感谢了!❤️❤️❤️ Spring Spring MVC MyBatis_冷兮雪的博客-CSDN博客 本章是讲Spring Boot 统⼀功能处理模块,也是 AOP 的实战环节&…...

LeetCode 每日一题 2023/8/14-2023/8/20
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 8/14 617. 合并二叉树8/15 833. 字符串中的查找与替换8/16 2682. 找出转圈游戏输家8/17 1444. 切披萨的方案数8/18 1388. 3n 块披萨8/19 2235. 两整数相加8/20 8/14 617. 合…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
