LeetCode 每日一题 2023/8/14-2023/8/20
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步
目录
- 8/14 617. 合并二叉树
- 8/15 833. 字符串中的查找与替换
- 8/16 2682. 找出转圈游戏输家
- 8/17 1444. 切披萨的方案数
- 8/18 1388. 3n 块披萨
- 8/19 2235. 两整数相加
- 8/20
8/14 617. 合并二叉树
dfs深搜
class TreeNode(object):def __init__(self, val=0, left=None, right=None):self.val = valself.left = leftself.right = right
def mergeTrees(root1, root2):""":type root1: TreeNode:type root2: TreeNode:rtype: TreeNode"""def func(n1,n2):if not n1:return n2if not n2:return n1node = TreeNode(n1.val+n2.val)node.left = func(n1.left,n2.left)node.right = func(n1.right,n2.right)return nodereturn func(root1,root2)8/15 833. 字符串中的查找与替换
op存放该位置能替换的数值
从头遍历每个位置
def findReplaceString(s, indices, sources, targets):""":type s: str:type indices: List[int]:type sources: List[str]:type targets: List[str]:rtype: str"""from collections import defaultdictn = len(s)op = defaultdict(list)for i,ind in enumerate(indices):op[ind].append(i)ans = []i = 0while i<n:tag = Falseif i in op:for ind in op[i]:if s[i:i+len(sources[ind])]==sources[ind]:tag = Trueans.append(targets[ind])i+=len(sources[ind])breakif not tag:ans.append(s[i])i+=1return "".join(ans)8/16 2682. 找出转圈游戏输家
模拟
def circularGameLosers(n, k):""":type n: int:type k: int:rtype: List[int]"""do = [False]*ncur = 0i=1while not do[cur]:do[cur]=Truecur+=i*kcur%=ni+=1return [i+1 for i in range(n) if not do[i]]8/17 1444. 切披萨的方案数
动态规划 dp[k][i][j] 表示把坐标(i,j)右下方切割成k块的方案
def ways(pizza, k):""":type pizza: List[str]:type k: int:rtype: int"""mod = 10**9+7m,n=len(pizza),len(pizza[0])apples = [[0]*(n+1) for _ in range(m+1)]dp = [[[0 for j in range(n)] for i in range(m)] for _ in range(k+1)]for i in range(m-1,-1,-1):for j in range(n-1,-1,-1):apples[i][j] = apples[i][j+1]+apples[i+1][j]-apples[i+1][j+1]+(pizza[i][j]=='A')if apples[i][j]>0:dp[1][i][j] = 1 else:dp[1][i][j] = 0for t in range(1,k+1):for i in range(m):for j in range(n):for ii in range(i+1,m):if apples[i][j]>apples[ii][j]:dp[t][i][j] = (dp[t][i][j]+dp[t-1][ii][j])%modfor jj in range(j+1,n):if apples[i][j]>apples[i][jj]:dp[t][i][j] = (dp[t][i][j]+dp[t-1][i][jj])%modreturn dp[k][0][0]8/18 1388. 3n 块披萨
可转换为在3n个数中 选择n个不相邻的数 和最大
动态规划dp[i][j]表示前i个数选择j个不相邻的数 最大和
def maxSizeSlices(slices):""":type slices: List[int]:rtype: int"""def func(slices):m = len(slices)n = (len(slices)+1)//3dp = [[float("-inf") for _ in range(n+1)] for _ in range(m)]dp[0][0] = 0dp[0][1] = slices[0]dp[1][0] = 0dp[1][1] = max(slices[0],slices[1])for i in range(2,m):dp[i][0] = 0for j in range(1,n+1):dp[i][j] = max(dp[i-1][j],dp[i-2][j-1]+slices[i])return dp[m-1][n]return max(func(slices[1:]),func(slices[0:-1]))8/19 2235. 两整数相加
如题相加
def sum(num1, num2):""":type num1: int:type num2: int:rtype: int"""return num1+num28/20
相关文章:

LeetCode 每日一题 2023/8/14-2023/8/20
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 8/14 617. 合并二叉树8/15 833. 字符串中的查找与替换8/16 2682. 找出转圈游戏输家8/17 1444. 切披萨的方案数8/18 1388. 3n 块披萨8/19 2235. 两整数相加8/20 8/14 617. 合…...

进入微服务阶段后的学习方法
微服务SpringCloud学习的特点 陌生,多,复杂。 技术陌生,技术栈多,实现复杂。 学习方式 对于每一个组件: 1.知道是什么、有什么用 2.知道操作步骤(跟着讲义操作即可),包括&#…...

C/C++中const关键字详解
为什么使用const?采用符号常量写出的代码更容易维护;指针常常是边读边移动,而不是边写边移动;许多函数参数是只读不写的。const最常见用途是作为数组的界和switch分情况标号(也可以用枚举符代替),分类如下:…...
【2023新教程】树莓派4B开机启动-树莓派第一次启动-树莓派不使用显示器启动-树莓派从购买到启动一步一步完全版!
背景 闲来无事,在咸鱼上买了一个树莓派4B。买来配件都十分齐全,于是就想着启动来测试一下。下面是树莓派无显示器第一次启动的全过程,包含安装系统。 网上的教程大多需要额外使用显示器、鼠标、键盘之类的外设。然而,树莓派本身就…...

LA@2@1@线性方程组和简单矩阵方程有解判定定理
文章目录 矩阵方程有解判定定理线性方程组有解判定特化:齐次线性方程组有解判定推广:矩阵方程 A X B AXB AXB有解判定证明推论 矩阵方程有解判定定理 线性方程组有解判定 线性方程组 A x b A\bold{x}\bold{b} Axb有解的充分必要条件是它的系数矩阵A和增广矩阵 ( A , b ) (A,…...

如何使用ChatGPT创作一个小说式的虚构的世界
世界构建也许是小说写作中最重要的一环,但也可能非常耗时。让ChatGPT加快这一过程吧。 写小说最棒的一点就是有机会从零开始创造一个新世界。你可以创造超凡脱俗的景观,赋予人物魔法。神话故事可以存在于你小说中的现实世界,而传统可以帮助你…...

用于量子通信和互联网的光量子芯片
近年来,新兴的光量子芯片在量子通信和量子互联网领域取得了重大进展。光量子芯片芯片具有可扩展、稳定和低成本等特点,为微型化应用开辟了新的可能性。 7月14日,一篇发表在《light: science & applications》的文章概述了用于量子通信的光…...
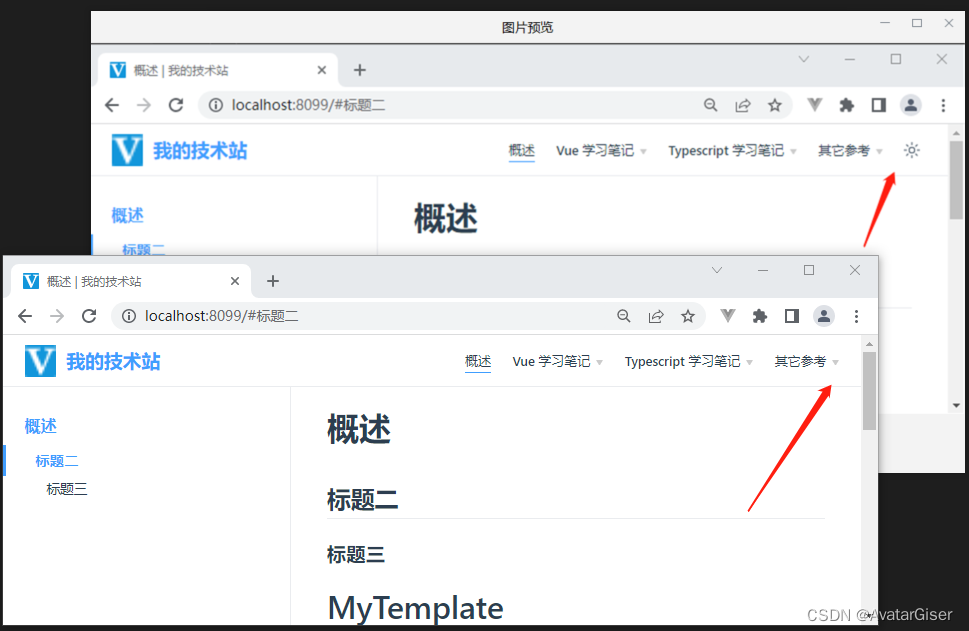
11. Vuepress2.x 关闭夜间模式
修改 docs/.vuepress/config.ts 配置文件 设置 themeConfig.darkMode属性详见 官网 module.exports {host: localhost, // ipport: 8099, //端口号title: 我的技术站, // 设置网站标题description: 描述:我的技术站,base: /, //默认路径head: [// 设置 favor.ico&a…...

netty实现websocket通信
调用注意: 1、端口一定要是可以访问的。 2、依赖必须注意和其他版本冲突,比如redis的springboot starter包,会与5.0版本冲突。 <netty.version>4.1.74.Final</netty.version> <dependency><groupId>io…...

两个list如何根据一个list中的属性去过滤掉另一个list中不包含这部分的属性,用流实现
你可以使用Java 8的流来实现这个功能。假设你有两个包含对象的List,每个对象有一个属性,你想根据一个List中的属性值来过滤掉另一个List中不包含这个属性值的对象。下面是一种使用流的方式来实现这个功能 import java.util.ArrayList; import java.util…...
Blender 混合现实3D模型制作指南【XR】
本教程分步展示如何: 减少 3D 模型的多边形数量,使其满足 Microsoft Dynamics 365 Guides 和使用 Microsoft Power Apps 创建的应用程序中包含的混合现实组件的特定性能目标的性能需求。将 3D 模型的多种材质(颜色)组合成可应用于…...
)
kubeasz在线安装K8S集群单master集群(kubeasz安装之二)
一、介绍 Kubeasz 是一个基于 Ansible 自动化工具,用于快速部署和管理 Kubernetes 集群的工具。它支持快速部署高可用的 Kubernetes 集群,支持容器化部署,可以方便地扩展集群规模,支持多租户,提供了强大的监控和日志分…...

『C语言』数据在内存中的存储规则
前言 小羊近期已经将C语言初阶学习内容与铁汁们分享完成,接下来小羊会继续追更C语言进阶相关知识,小伙伴们坐好板凳,拿起笔开始上课啦~ 一、数据类型的介绍 我们目前已经学了基本的内置类型: char //字符数据类型 short …...
基于ssm+vue的新能源汽车在线租赁管理系统源码和论文PPT
基于ssmvue的新能源汽车在线租赁管理系统源码和论文PPT010 开发环境: 开发工具:idea 数据库mysql5.7(mysql5.7最佳) 数据库链接工具:navcat,小海豚等 开发技术:java ssm tomcat8.5 摘 要 随着科学技术的飞速发展࿰…...

深入解析IDS/IPS与SSL/TLS和网络安全
目录 防火墙 IDS IPS DMZ VPN VPS SSL/TLS 动态IP 静态IP 防火墙 防火墙是一种网络安全设备,用于监控和控制网络流量,保护网络免受未经授权的访问、恶意攻击和威胁。防火墙可以基于规则进行数据包过滤,允许或阻止特定类型的流量通过…...
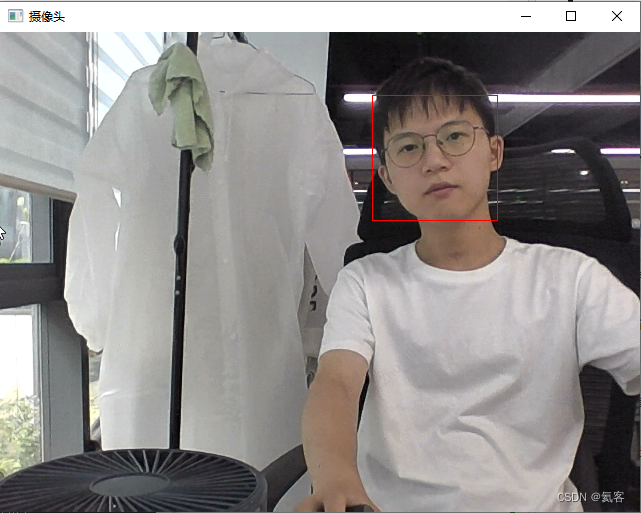
在Visual Studio上,使用OpenCV实现人脸识别
1. 环境与说明 本文介绍了如何在Visual Studio上,使用OpenCV来实现人脸识别的功能 环境说明 : 操作系统 : windows 10 64位Visual Studio版本 : Visual Studio Community 2022 (社区版)OpenCV版本 : OpenCV-4.8.0 (2023年7月最新版) 实现效果如图所示࿰…...
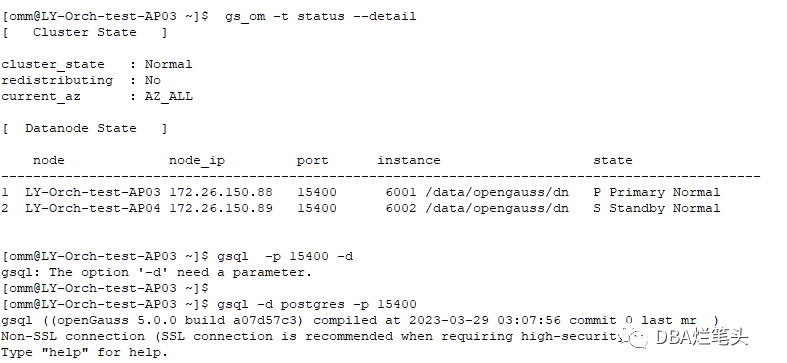
搭建openGauss 5.0 一主一从复制集群
openGauss是一款支持SQL2003标准语法,支持主备部署的高可用关系型国产数据库。 多种存储模式支持复合业务场景,新引入提供原地更新存储引擎。NUMA化数据结构支持高性能。Paxos一致性日志复制协议,主备模式,CRC校验支持高可用。支…...
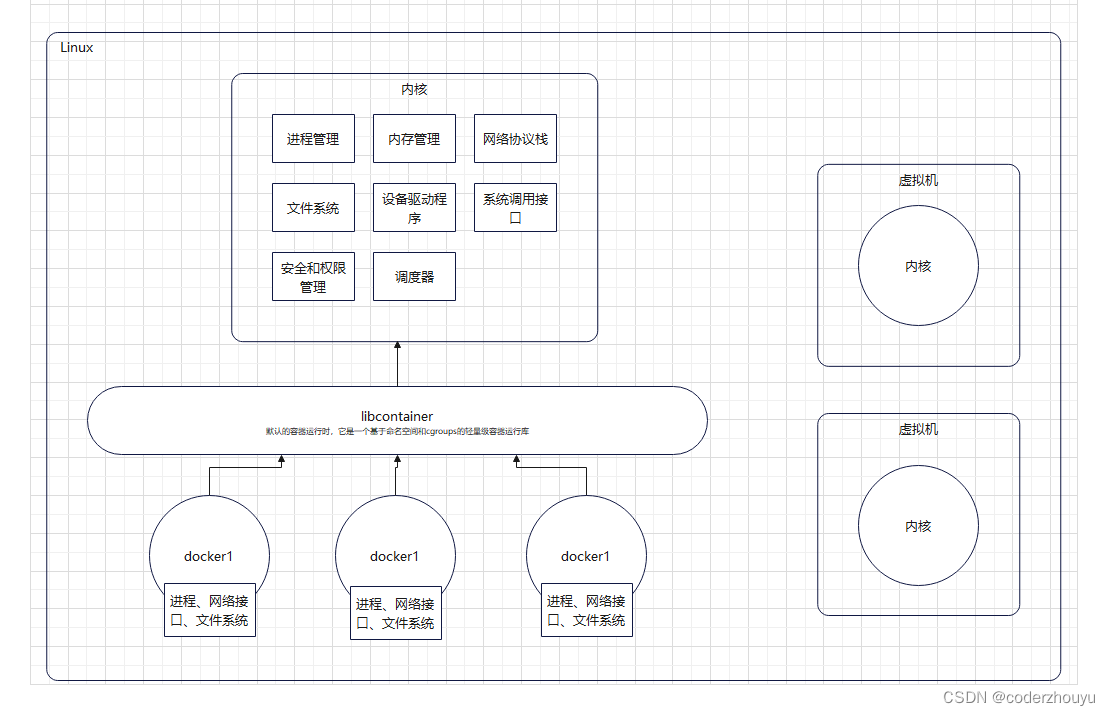
Docker碎碎念
docker和虚拟机的区别 虚拟机(VM)是通过在物理硬件上运行一个完整的操作系统来实现的。 每个虚拟机都有自己的内核、设备驱动程序和用户空间,它们是相互独立且完全隔离的。 虚拟机可以在不同的物理服务器之间迁移,因为它们是以整…...

【C++】extern
目录 1. 变量声明和定义的关系 2. 默认状态下,const对象仅在文件内有效 3. 链接指示:extern "C" 3.1 声明一个非C的函数 3.2 链接指示与头文件 3.3 指向extern "C"函数的指针 3.4 链接指示对整个声明都有效 3.5 导出C函数到…...
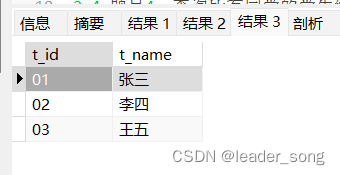
2023全网Mysql 合集(25w字)附课程 从安装到高级,实战
mysql学习 1.安装mysql 安装教程 2.mysql的详细学习教程 mysql的详细教程 3.mysql 的高级优化 MySQL高级篇(SQL优化、索引优化、锁机制、主从复制) 4.MySQL 面试 MySQL数据库面试题总结 二.mysql实战 一、创建数据表并插入数据 1、学生表 Stud…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
