『C语言』数据在内存中的存储规则

前言
小羊近期已经将C语言初阶学习内容与铁汁们分享完成,接下来小羊会继续追更C语言进阶相关知识,小伙伴们坐好板凳,拿起笔开始上课啦~
一、数据类型的介绍
我们目前已经学了基本的内置类型:
char //字符数据类型
short //短整型
int //整形
long //长整型
long long //更长的整形
float //单精度浮点数
double //双精度浮点数
类型的基本归类
整形家族:
char:unsigned charsigned char
short:unsigned short[int]signed short[int]
int:unsigned intsigned int
long:unsigned long[int]signed long[int]
unsigned:无符号数类型
当一个数是无符号类型时,那么其最高位的1或0,和其它位一样,用来表示该数的大小。
signed:有符号数类型
当一个数是有符号类型时,最高数称为“符号位”。符号位为1时,表示该数为负数,为0时表示为正数。
注意:有符号类型可以表示正数,负数或0,无符号类型仅能表示大于等于0的值
浮点型家族:
float
double
构造类型:
//数组类型
struct //结构体类型
enum //枚举类型
union //联合类型
指针类型:
int* p;
char* p;
float* p;
void* p;
空类型:
void//(空类型)
二、整型在内存中的存储
以整型int为例,我们都知道常见的编译器中int占四个字节,那么计算机中这四个字节是如何将数据存储下来的呢?
那我们先了解一下机器数和真值的概念,再去了解原码,反码,补码的概念
2.1 机器数
一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是带符号的,在计算机中 用机器数的最高位存放符号,正数为0,负数为1。
例如:
+ 3的机器数:0000 0011
- 3的机器数:1000 0011
2.2 真值
因为第一位是符号位,所以机器数的形式值就不等于真正的数值。所以,为区别起见,将带符号位的机器数对应的真正数值称为机器数的真值。
例如:
0000 0001的真值 = +000 0001 = +1
1000 0001的真值 = -000 0001 = -1
2.3 原码、反码、补码
对于一个数,计算机要使用一定的编码方式进行存储,原码、反码、补码是机器存储一个具体数字的编码方式。
三种方式均有符号位和数值位两部分,符号位都是0表示“正数”,1表示“负数”,而数值位分正负数而定。
正数的原码、反码、补码都相同,负数的原码、反码、补码各不相同
原码:
直接将数值按照正负数的形式翻译成二进制就可以得到原码
反码:
将原码的符号位不变,其他位次按位取反
补码:
反码符号位不变,数值为+1
反码回到原码的两种方式:
1、补码-1后 取反得到原码
2、补码取反后 +1得到原码
对于整形来说:数据存放内存中其实存放的是补码,那这又是为什么呢?
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数
值域统一处理;同时,加法和减法也可以统一处理(CPU只有加法器 )此外,补码与原码相
互转换,其运算过程是相同的,不需要额外的硬件电路。
我们看看在内存中的存储:
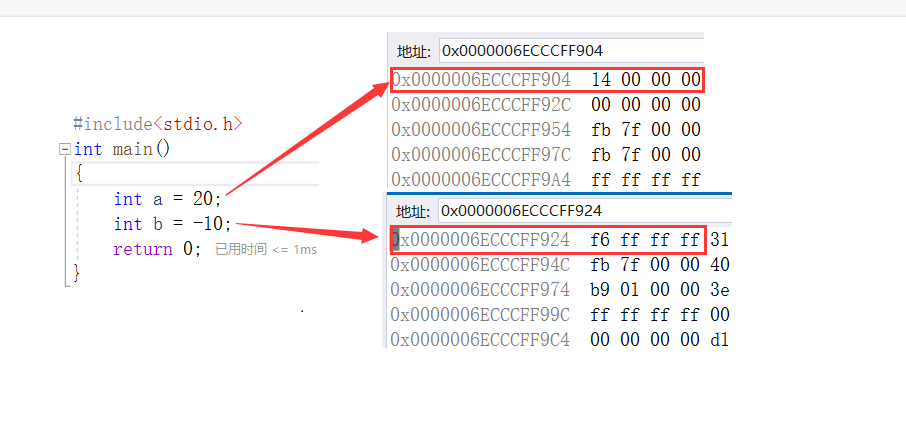
我们知道内存中a和b存储的是补码,但我们发现存储的顺序有点不对劲。
-10在内存中存储应该是FFFFFFF6,而我们看到的是F6FFFFFF。
这里小羊呢,就为铁汁们了解一下大小端
2.4 大小端介绍
什么是大小端:
大端存储模式:指数据的低位保存在内存的高地址中,而数据的高位保存在内存的低地址中
小端存储模式:指数据的低位保存在内存的低地址中,而数据的高位保存在内存的高地址中
例如:
数字0x12 34 56 78在内存中:
大端模式:(我们通常直观上认为的模式)
低地址 --------------------> 高地址0x12 | 0x34 | 0x56 | 0x78
小端模式:
低地址 --------------------> 高地址0x78 | 0x56 | 0x34 | 0x12
** 为什么会有大端和小端呢?**
因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节,一个字节为8bit。但是在C语言中除了8 bit的char之外,还有16 bit的short型,32 bit的long型(要看具体的编译器),另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于一个字节,那么必然存在着一个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。
如何判断大小端的代码:
#include<stdio.h>
int main()
{int i = 1;//0000 0001char* p = &i;if (*p == 1)//若第一个地址存的是1,即为小端,反则大端printf("小端");elseprintf("大端";return 0;
}
自定义函数测试:
#include<stdio.h>int check_sys()
{int a = 1;char* p = (char*)&a;if (*p == 1)return 1;elsereturn 0;
}int main()
{if (check_sys() == 1)printf("小端");elseprintf("大端");return 0;
}
三、浮点数在内存中的存储
#include<stdio.h>
int main()
{int n = 9;float* p = (float*)&n;printf("n的值为:%d\n", n);printf("*p的值为:%f\n", *p);*p = 9.0;printf("n的值为:%d\n", n);printf("*p的值为:%f\n", *p);return 0;
}
我们先试着猜一下结果
输出显示:
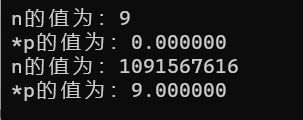
怎么样,这个结果是不是有点出乎意料!那么就跟着小羊来学习浮点数的存储规则吧。
3.1浮点数存储规则
浮点数存储形式:
根据国际标准IEEE(电子和电子工程协会)754,任意一个二进制浮点数V可以表示为下面的形式:
(-1) ^ S * M * 2 ^ E
1. (-1) ^ S 表示符号位,当S=0时,V为正数;当S=1时,V为负数
2. M 表示有效数字,且1 <= M <2
3. 2 ^ E表示指数位
例如:
- 十进制的5.0,写成二进制是0101 ------> 1.10x2^2
可以得出s=0,M=1.01,E=2 - 十进制的-7.0,写成二进制是0111 ------->1.11x2^2
可以得出s=-1,M=1.11,E=2
IEEE 754 规定:
对于 32 位的浮点数(单精度),最高的 1 位是符号位 s ,接着的 8 位是指数 E ,剩下的 23位为有效数字 M 。

对于 64 位的浮点数(双精度),最高的 1 位是符号位S,接着的 11 位是指数 E ,剩下的 52 位为有效数字 M 。
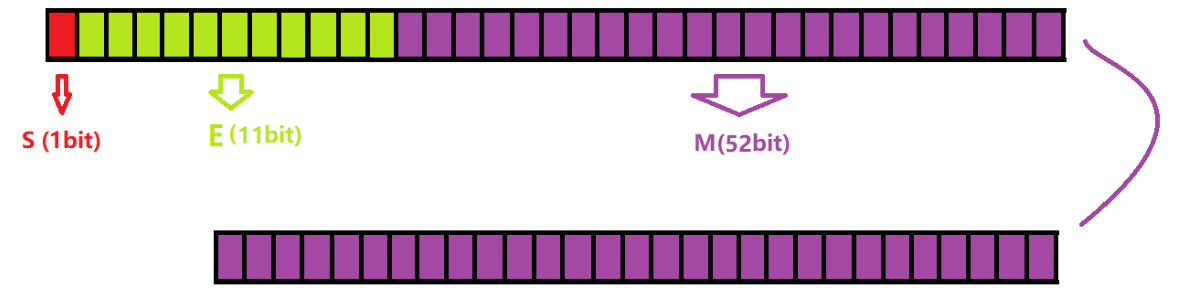
IEEE 754 对有效数字** M **和指数 E ,还有一些特别规定。
前面说过, 1≤M<2 ,也就是说, M 可以写成 1.xxxxxx 的形式,其中 xxxxxx 表示小数部分。
IEEE 754 规定,在计算机内部保存 M 时,默认这个数的第一位总是 1 ,因此可以被舍去,只保存后面的xxxxxx部分。比如保存 1.01 的时候,只保存01 ,等到读取的时候,再把第一位的 1 加上去。这样做的目的,是节省 1 位有效数字。以 32 位浮点数为例,留给M 只有 23 位,将第一位的1 舍去后等于可以保存 24 位有效数字。
至于指数 E ,情况就比较复杂。首先, E 为一个无符号整数( unsigned int )
这意味着,如果 E 为 8 位,它的取值范围为 0~255 ;如果 E 为 11 位,它的取值范围为 0~2047 。但是我们知道,科学计数法中的E 是可以出现负数的,所以IEEE 754 规定,存入内存时 E 的真实值必须再加上一个中间数,对于 8 位的 E ,这个中间数是127 ;对于 11 位的 E ,这个中间数是1023 。比如 2^10的 E 是 10 ,所以保存成 32 位浮点数时,必须保存成 10+127=137 ,即10001001。
3.2 浮点型的读取
我们知道浮点型在内存中的存储后,将步骤反过来就是取出的过程。
1、有效数字M:
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存小数部分。比如保存1.0110001101时,只保存0110001101,后面的位数补0就可以了,等到读取的时候,再把第一位的1补上去。
2、指数E
E为一个无符号整数(unsigned int)根据指数域不同取值分为一下三种情况:
1)E不全为0或不全为1(规格化值)
这是最常见情况,取出内存中的数时,指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1。
2)E全为0(非规格化值)
这时,浮点数的指数E等于1-127(或1-1023)即为真实值,有效数字M不再加上第一位的1,而是还原为0.xxxxxxx的小数。这样做是为了表示正负零,以及接近于0的很小的数字。
3)E全为1(特殊数值)
当指数域全为1时属于这种情形。此时,如果小数域全为0且符号域S=0,则表示正无穷,如果小数域全为0且符号域S=1,则表示负无穷。如果小数域不全为0时,浮点数将被解释为NaN, 即不是一个数(Not a Number)
解释前面的题目:
整形9以浮点型打印
整形存储,浮点型打印
0000 0000 0000 0000 0000 0000 0000 1001
浮点型读取:
s=0,M=000 0000 0000 0000 0000 0110,E=0000 0000(E全为0)
所以结果为:0.0000(近于0的很小的数字)现在看例题的第二部:
浮点数9.0以整形打印
9.0 -> 1001.0 -> (-1)^0*1.001*2^3 -> s=0,M=1.001,E=,3+127=130
所以第一位的符号位s=0,有效数字M为001后面在加20个0,凑满23位,指数E为3+127=130,即10000010
所以写成S+E+M:
0 10000010 001 0000 0000 0000 0000 0000
这32位的二进制数,还原成十进制,正是1091567616
总结
希望看完这篇文章对铁汁们有所帮助,小羊后续还会持续更新C语言的学习知识,希望小伙伴们给个支持,来个一键三连~

相关文章:

『C语言』数据在内存中的存储规则
前言 小羊近期已经将C语言初阶学习内容与铁汁们分享完成,接下来小羊会继续追更C语言进阶相关知识,小伙伴们坐好板凳,拿起笔开始上课啦~ 一、数据类型的介绍 我们目前已经学了基本的内置类型: char //字符数据类型 short …...
基于ssm+vue的新能源汽车在线租赁管理系统源码和论文PPT
基于ssmvue的新能源汽车在线租赁管理系统源码和论文PPT010 开发环境: 开发工具:idea 数据库mysql5.7(mysql5.7最佳) 数据库链接工具:navcat,小海豚等 开发技术:java ssm tomcat8.5 摘 要 随着科学技术的飞速发展࿰…...

深入解析IDS/IPS与SSL/TLS和网络安全
目录 防火墙 IDS IPS DMZ VPN VPS SSL/TLS 动态IP 静态IP 防火墙 防火墙是一种网络安全设备,用于监控和控制网络流量,保护网络免受未经授权的访问、恶意攻击和威胁。防火墙可以基于规则进行数据包过滤,允许或阻止特定类型的流量通过…...
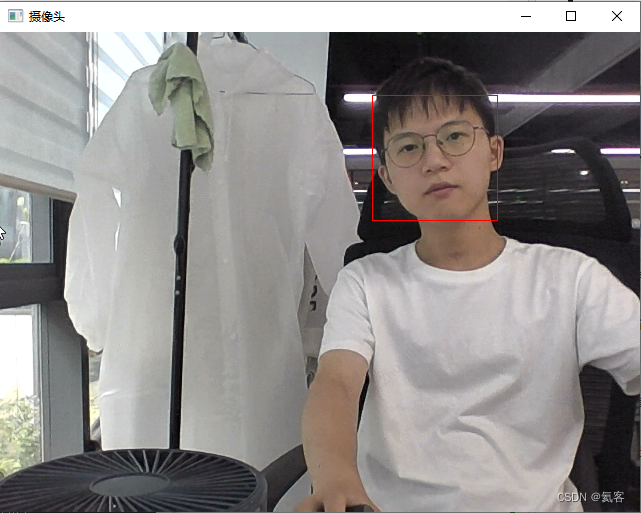
在Visual Studio上,使用OpenCV实现人脸识别
1. 环境与说明 本文介绍了如何在Visual Studio上,使用OpenCV来实现人脸识别的功能 环境说明 : 操作系统 : windows 10 64位Visual Studio版本 : Visual Studio Community 2022 (社区版)OpenCV版本 : OpenCV-4.8.0 (2023年7月最新版) 实现效果如图所示࿰…...
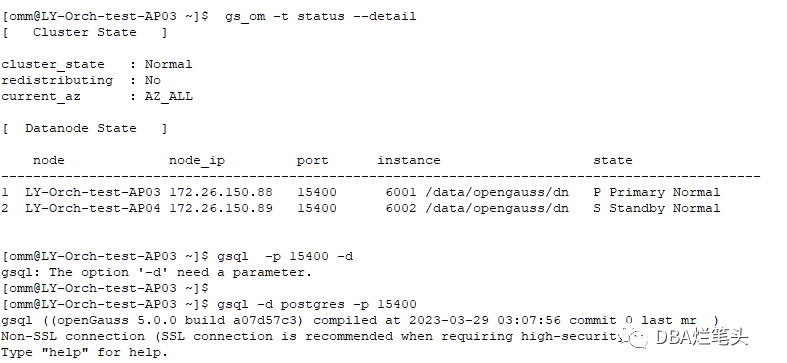
搭建openGauss 5.0 一主一从复制集群
openGauss是一款支持SQL2003标准语法,支持主备部署的高可用关系型国产数据库。 多种存储模式支持复合业务场景,新引入提供原地更新存储引擎。NUMA化数据结构支持高性能。Paxos一致性日志复制协议,主备模式,CRC校验支持高可用。支…...
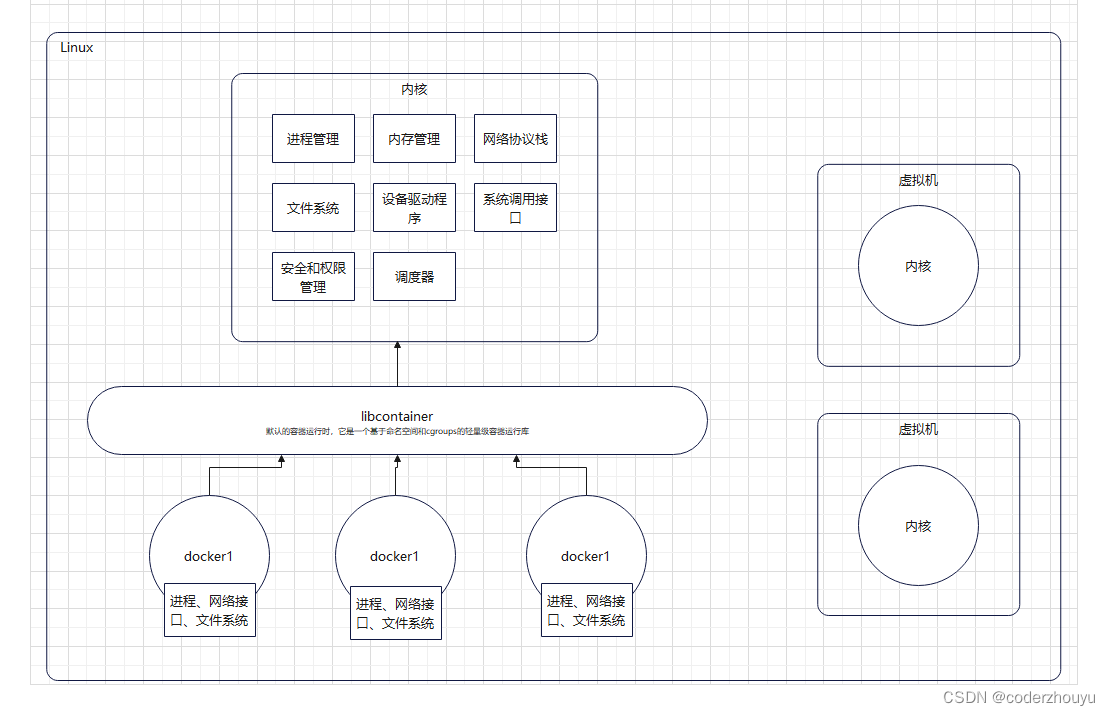
Docker碎碎念
docker和虚拟机的区别 虚拟机(VM)是通过在物理硬件上运行一个完整的操作系统来实现的。 每个虚拟机都有自己的内核、设备驱动程序和用户空间,它们是相互独立且完全隔离的。 虚拟机可以在不同的物理服务器之间迁移,因为它们是以整…...

【C++】extern
目录 1. 变量声明和定义的关系 2. 默认状态下,const对象仅在文件内有效 3. 链接指示:extern "C" 3.1 声明一个非C的函数 3.2 链接指示与头文件 3.3 指向extern "C"函数的指针 3.4 链接指示对整个声明都有效 3.5 导出C函数到…...
2023全网Mysql 合集(25w字)附课程 从安装到高级,实战
mysql学习 1.安装mysql 安装教程 2.mysql的详细学习教程 mysql的详细教程 3.mysql 的高级优化 MySQL高级篇(SQL优化、索引优化、锁机制、主从复制) 4.MySQL 面试 MySQL数据库面试题总结 二.mysql实战 一、创建数据表并插入数据 1、学生表 Stud…...
张俊林:由ChatGPT反思大语言模型(LLM)的技术精要
转自:https://mp.weixin.qq.com/s/eMrv15yOO0oYQ-o-wiuSyw 导读:ChatGPT出现后惊喜或惊醒了很多人。惊喜是因为没想到大型语言模型(LLM,Large Language Model)效果能好成这样;惊醒是顿悟到我们对LLM的认知及发展理念&a…...

单机编排docker compose
Docker之旅(8)-单机编排docker compose 当在宿主机启动较多的容器时候,如果都是手动操作会觉得比较麻烦而且容易出错, 并且每个容器之间也会有先后启动的顺序依赖等。这个时候推荐使用 docker 单机 编排工具 docker-compose,docker-compose …...

C++ 面向对象三大特性——多态
✅<1>主页:我的代码爱吃辣 📃<2>知识讲解:C 继承 ☂️<3>开发环境:Visual Studio 2022 💬<4>前言:面向对象三大特性的,封装,继承,多态ÿ…...

相同数字的积木游戏
题目描述 题目描述 小华和小薇一起通过玩积木游戏学习数学。 他们有很多积木,每个积木块上都有一个数字,积木块上的数字可能相同。 小华随机拿一些积木挨着排成一排,请小薇找到这排积木中数字相同目所处位置最远的2块积木块,计算…...
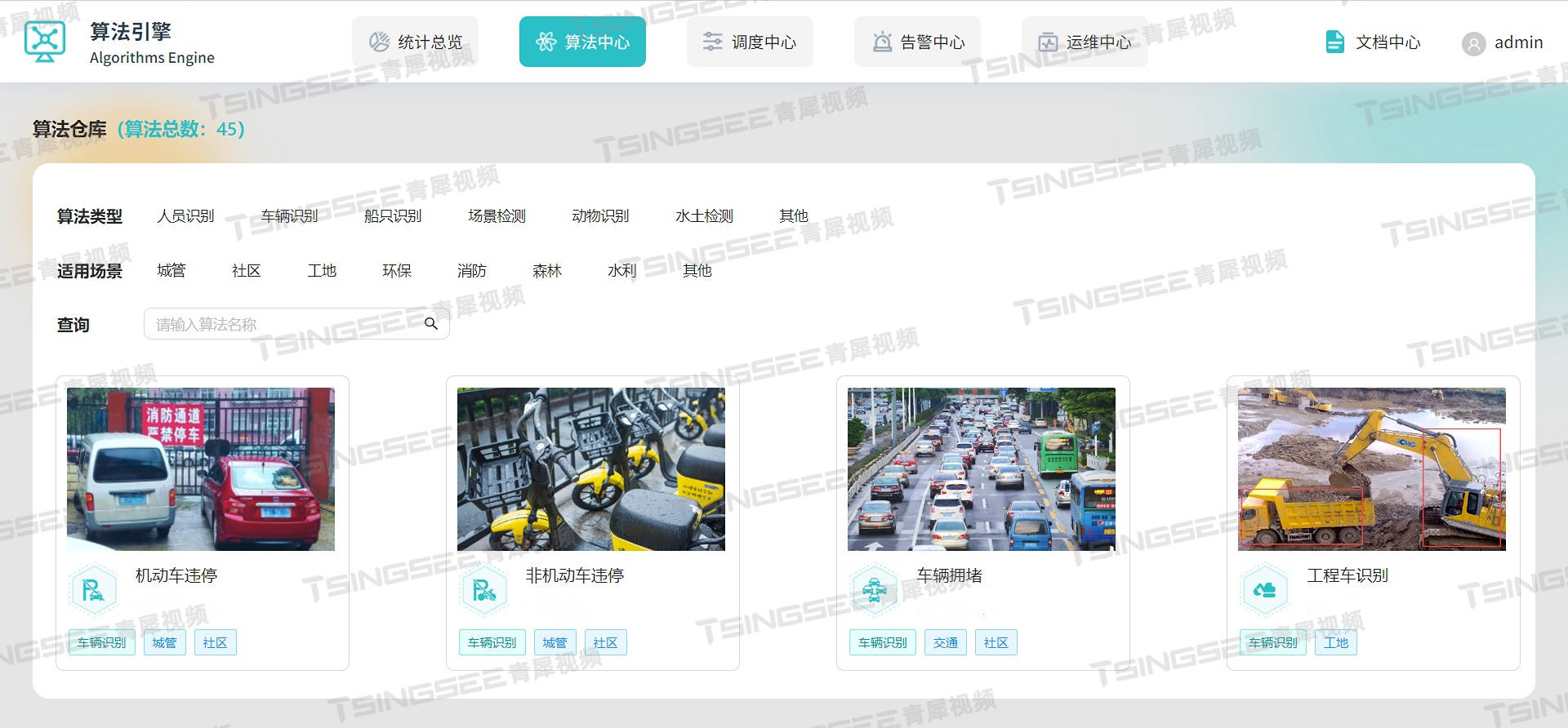
安防监控视频云存储EasyCVR平台H.265转码功能更新:新增分辨率配置
安防视频集中存储EasyCVR视频监控综合管理平台可以根据不同的场景需求,让平台在内网、专网、VPN、广域网、互联网等各种环境下进行音视频的采集、接入与多端分发。在视频能力上,视频云存储平台EasyCVR可实现视频实时直播、云端录像、视频云存储、视频存储…...
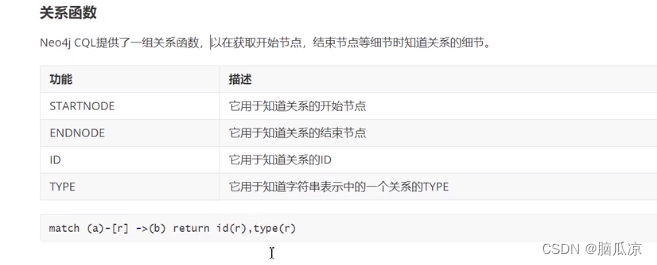
图数据库_Neo4j学习cypher语言_常用函数_关系函数_字符串函数_聚合函数_数据库备份_数据库恢复---Neo4j图数据库工作笔记0008
然后再来看一些常用函数,和字符串函数,这里举个例子,然后其他的 类似 可以看到substring字符串截取函数 可以看到截取成功 聚合函数 这里用了一个count(n) 统计函数,可以看到效果 关系函数,我们用过就是id(r) 可以取出对应的r的id来这样.....
)
LeetCode150道面试经典题-- 加一(简单)
1.题目 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以零开头。 2.示例 示例 1: 输入&am…...
Centos7 配置Docker镜像加速器
docker实战(一):centos7 yum安装docker docker实战(二):基础命令篇 docker实战(三):docker网络模式(超详细) docker实战(四):docker架构原理 docker实战(五):docker镜像及仓库配置 docker实战(六):docker 网络及数据卷设置 docker实战(七):docker 性质及版本选择 认知升…...

微信小程序中pdf的上传、下载及excel导出
微信小程序中pdf的上传、下载及excel导出 pdf上传上传1:上传2: pdf下载导出excel pdf上传 上传两种方法: 上传1: 1.用vant weapp组件: //pdf上传--vant weapp组件 <view class"content"><van-u…...
Python_11 类的方法
一、查缺补漏 1. 实例方法必须用类实例化对象()来调用,用类来调用时会执行,但是self中不是实例化类地址而是传的字符串 二、类中的方法 1. 实例方法 1. 定义在类里面的普通方法(函数) 2. 第一个参数必须是类实例,在方法调用的时候会自动…...
——Centos7更新)
CentOS系统环境搭建(一)——Centos7更新
Centos7更新 更新 yum(包括centos内核) yum update执行后,系统将更新到centos 7.9。 从这一篇文章开始开始,我将开始在centos系统环境搭建🔗https://blog.csdn.net/weixin_43982359/category_12411496.html中开始对C…...
Mariadb高可用MHA
目录 前言 一、概述 (一)、概念 (二)、组成 (三)、特点 (四)、工作原理 二、案例 (一)、构建MHA 1.所有节点ssh免密登录 2、MySQL主从复制 &#x…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
