LA@2@1@线性方程组和简单矩阵方程有解判定定理
文章目录
- 矩阵方程有解判定定理
- 线性方程组有解判定
- 特化:齐次线性方程组有解判定
- 推广:矩阵方程 A X = B AX=B AX=B有解判定
- 证明
- 推论
矩阵方程有解判定定理
线性方程组有解判定
-
线性方程组 A x = b A\bold{x}=\bold{b} Ax=b有解的充分必要条件是它的系数矩阵A和增广矩阵 ( A , b ) (A,\bold{b}) (A,b)具有相同的秩 R ( A ) = R ( A , b ) R(A)=R(A,\bold{b}) R(A)=R(A,b),记 r = R ( A ) = R ( A , b ) r=R(A)=R(A,\bold{b}) r=R(A)=R(A,b):
- 若 r = n r=n r=n有方程组有唯一解
- 若 r < n r<{n} r<n方程组有多解
-
对于非齐次线性方程,需要计算 R ( A ) , R ( A , b ) R(A),R(A,\bold{b}) R(A),R(A,b)
-
对于齐次线性方程只需要计算 R ( A ) R(A) R(A)
特化:齐次线性方程组有解判定
-
这是线性方程组有解的特例,可以将定理进一步简化
-
齐次线性方程组 A x = 0 A\bold{x}=\bold{0} Ax=0齐次方程组的情况可以理解为 b \bold{b} b中元素全为0
-
容易知道 A x = 0 A\bold{x}=\bold{0} Ax=0总有 R ( A ) = R ( A ‾ ) = r R(A)=R(\overline{A})=r R(A)=R(A)=r,因此齐次线性方程组总是有解;
- 我们只需要计算系数矩阵 A A A的秩 R ( A ) R(A) R(A)即可得到 r r r
- 若 r = n r=n r=n则方程组有唯一解,并且是零解
- 若 r < n r<n r<n方程组有非零解
-
齐次线性方程组有解判定定理:齐次线性方程组 A x = 0 A\bold{x}=\bold{0} Ax=0有解的充要条件是 R ( A ) ⩽ n R(A)\leqslant{n} R(A)⩽n;
- 有零解(唯一解)的充要条件是 R ( A ) = n R(A)=n R(A)=n
- 有非零解(多解)的充要条件是 R ( A ) < n R(A)<n R(A)<n;
推广:矩阵方程 A X = B AX=B AX=B有解判定
- 这里 B B B是常数项矩阵(不再是系数矩阵的增广矩阵)
- 定理:矩阵方程 A X = B AX=B AX=B有解的充要条件是 R ( A ) = R ( A , B ) R(A)=R(A,B) R(A)=R(A,B)
-
注意这里 X , B X,B X,B不一定是向量,可能是多行多列的矩阵
-
参考同济线代v6@p76@定理6
-
证明
-
设 A , X , B A,X,B A,X,B分别为 m × n m\times{n} m×n, n × l n\times{l} n×l, m × l m\times{l} m×l的矩阵
-
对X和B按列分块:
- X X X= ( x 1 , x 2 , ⋯ x l ) (\bold{x}_1,\bold{x}_2,\cdots \bold{x}_l) (x1,x2,⋯xl),
- B B B= ( b 1 , b 2 , ⋯ b l ) (\bold{b}_1,\bold{b}_2,\cdots \bold{b}_l) (b1,b2,⋯bl)
-
矩阵方程 A X = B AX=B AX=B等价于 l l l个向量方程(线性方程组)
-
A X = A ( x 1 , x 2 , ⋯ x l ) AX=A(\bold{x}_1,\bold{x}_2,\cdots \bold{x}_l) AX=A(x1,x2,⋯xl)= ( A x 1 , A x 2 , ⋯ A x l ) (A\bold{x}_1,A\bold{x}_2,\cdots A\bold{x}_l) (Ax1,Ax2,⋯Axl)
-
所有 A X = B AX=B AX=B等价于 ( A x 1 , A x 2 , ⋯ A x l ) (A\bold{x}_1,A\bold{x}_2,\cdots A\bold{x}_l) (Ax1,Ax2,⋯Axl)= ( b 1 , b 2 , ⋯ b l ) (\bold{b}_1,\bold{b}_2,\cdots \bold{b}_l) (b1,b2,⋯bl)
- 又等价于 A x i = b i ( i = 1 , 2 , ⋯ , l ) A\bold{x}_i=\bold{b}_i(i=1,2,\cdots,l) Axi=bi(i=1,2,⋯,l)共 l l l个线性方程组
- 这些线性方程的共同点是有相同的系数矩阵 A A A,这意味着这 l l l个线性方程组以及原矩阵方程的系数矩阵的秩都是相等的,这个结论很重要
- 而位置数矩阵和常数项矩阵又是相对独立的
-
设 R ( A ) = r R(A)=r R(A)=r,且 A A A的行阶梯形矩阵为 A ~ \widetilde{A} A ,则 A ~ \widetilde{A} A 有 r r r个非零行,且 A ~ \widetilde{A} A 的后 m − r m-r m−r行为全零行
-
( A , B ) (A,B) (A,B)= ( A , b 1 , b 2 , ⋯ b l ) (A,\bold{b}_1,\bold{b}_2,\cdots \bold{b}_l) (A,b1,b2,⋯bl) ∼ r \overset{r}{\sim} ∼r ( A ~ , b 1 ~ , ⋯ , b l ~ ) {(\widetilde{A},\widetilde{\bold{b}_1},\cdots,\widetilde{\bold{b}_l})} (A ,b1 ,⋯,bl )
- 其中 A ~ \widetilde{A} A 是 A A A的行阶梯形矩阵
- 而向量 b 1 ~ , ⋯ , b l ~ \widetilde{\bold{b}_1},\cdots,\widetilde{\bold{b}_l} b1 ,⋯,bl 是 b 1 , b 2 , ⋯ b l \bold{b}_1,\bold{b}_2,\cdots \bold{b}_l b1,b2,⋯bl与 A ∼ r A ~ A\overset{r}{\sim}\widetilde{A} A∼rA 执行相同的行变换后的结果,即 b i ~ \widetilde{\bold{b}_i} bi 并不表示某个行阶梯形矩阵
-
将等价的第 i i i个线性方程组的增广矩阵初等行变换为行阶梯形矩阵: ( A , b i ) (A,\bold{b}_i) (A,bi) ∼ r \overset{r}{\sim} ∼r ( A ~ , b i ~ ) {(\widetilde{A},\widetilde{\bold{b}_i})} (A ,bi ), ( i = 1 , 2 , ⋯ , l ) (i=1,2,\cdots,l) (i=1,2,⋯,l)
-
A X = B AX=B AX=B有解 ⇔ \Leftrightarrow ⇔ A x i = b i {A\bold{x}_i=\bold{b}_i} Axi=bi ( i = 1 , 2 , ⋯ , l ) (i=1,2,\cdots,l) (i=1,2,⋯,l)有解
- ⇔ \Leftrightarrow ⇔ R ( A , b i ) {R(A,\bold{b}_i)} R(A,bi)= R ( A ) = r R(A)=r R(A)=r, ( i = 1 , 2 , ⋯ , l ) (i=1,2,\cdots,l) (i=1,2,⋯,l)
- ⇔ \Leftrightarrow ⇔ b i ~ {\widetilde{\bold{b}_i}} bi 的后 m − r m-r m−r个分量(元)全为0 ( i = 1 , 2 , ⋯ , l ) (i=1,2,\cdots,l) (i=1,2,⋯,l)
- 因为,若后 m − r m-r m−r个元中存在非零元,会导致 R ( A , b i ) > R ( A ) R(A,\bold{b}_i)>R(A) R(A,bi)>R(A),导致 A x i = b i {A\bold{x}_i=\bold{b}_i} Axi=bi无解
- 而其前 r r r个元的取值情况不会影响 R ( A , b i ) {R(A,\bold{b}_i)} R(A,bi)= R ( A ) R(A) R(A)的成立,我们不关心
- ⇔ \Leftrightarrow ⇔ 矩阵 ( b 1 ~ , ⋯ , b l ~ ) (\widetilde{\bold{b}_1},\cdots,\widetilde{\bold{b}_l}) (b1 ,⋯,bl )的后 m − r m-r m−r行全为0;
- ⇔ \Leftrightarrow ⇔ 行阶梯形矩阵 D ~ \widetilde{D} D = ( A ~ , b 1 ~ , ⋯ , b l ~ ) (\widetilde{A},\widetilde{\bold{b}_1},\cdots,\widetilde{\bold{b}_l}) (A ,b1 ,⋯,bl )的后 m − r m-r m−r行全为0
- ⇔ \Leftrightarrow ⇔ R ( D ~ ) ⩽ m − ( m − r ) = r R(\widetilde{D})\leqslant{m-(m-r)=r} R(D )⩽m−(m−r)=r,又因为 D ~ \widetilde{D} D 包含了 A ~ \widetilde{A} A ,所以 R ( A ~ ) = r ⩽ R ( D ~ ) R(\widetilde{A})=r\leqslant{R(\widetilde{D})} R(A )=r⩽R(D )
- ⇔ \Leftrightarrow ⇔ R ( D ~ ) = r R(\widetilde{D})=r R(D )=r
- ⇔ R ( A , B ) = R ( A ) \Leftrightarrow{R(A,B)=R(A)} ⇔R(A,B)=R(A)
-
因此,如果 A X = B AX=B AX=B有解,则 R ( A , B ) = R ( A ) R(A,B)=R(A) R(A,B)=R(A)
推论
- 若 A X = B AX=B AX=B有解,则 R ( B ) ⩽ R ( A , B ) = R ( A ) R(B)\leqslant{R(A,B)}=R(A) R(B)⩽R(A,B)=R(A),所以 R ( B ) ⩽ R ( A ) R(B)\leqslant{R(A)} R(B)⩽R(A),即常数项矩阵的秩小于系数矩阵的秩
- 对 A X = B AX=B AX=B两边同时取转置运算,有 X T A T = B T X^TA^T=B^T XTAT=BT,同理有 R ( B T ) ⩽ R ( X T ) R(B^T)\leqslant R(X^T) R(BT)⩽R(XT),即 R ( B ) ⩽ R ( X ) R(B)\leqslant{R(X)} R(B)⩽R(X)
- 综上, R ( B ) ⩽ min ( R ( A ) , R ( X ) ) R(B)\leqslant{\min(R(A),R(X))} R(B)⩽min(R(A),R(X))
相关文章:

LA@2@1@线性方程组和简单矩阵方程有解判定定理
文章目录 矩阵方程有解判定定理线性方程组有解判定特化:齐次线性方程组有解判定推广:矩阵方程 A X B AXB AXB有解判定证明推论 矩阵方程有解判定定理 线性方程组有解判定 线性方程组 A x b A\bold{x}\bold{b} Axb有解的充分必要条件是它的系数矩阵A和增广矩阵 ( A , b ) (A,…...

如何使用ChatGPT创作一个小说式的虚构的世界
世界构建也许是小说写作中最重要的一环,但也可能非常耗时。让ChatGPT加快这一过程吧。 写小说最棒的一点就是有机会从零开始创造一个新世界。你可以创造超凡脱俗的景观,赋予人物魔法。神话故事可以存在于你小说中的现实世界,而传统可以帮助你…...

用于量子通信和互联网的光量子芯片
近年来,新兴的光量子芯片在量子通信和量子互联网领域取得了重大进展。光量子芯片芯片具有可扩展、稳定和低成本等特点,为微型化应用开辟了新的可能性。 7月14日,一篇发表在《light: science & applications》的文章概述了用于量子通信的光…...
11. Vuepress2.x 关闭夜间模式
修改 docs/.vuepress/config.ts 配置文件 设置 themeConfig.darkMode属性详见 官网 module.exports {host: localhost, // ipport: 8099, //端口号title: 我的技术站, // 设置网站标题description: 描述:我的技术站,base: /, //默认路径head: [// 设置 favor.ico&a…...

netty实现websocket通信
调用注意: 1、端口一定要是可以访问的。 2、依赖必须注意和其他版本冲突,比如redis的springboot starter包,会与5.0版本冲突。 <netty.version>4.1.74.Final</netty.version> <dependency><groupId>io…...

两个list如何根据一个list中的属性去过滤掉另一个list中不包含这部分的属性,用流实现
你可以使用Java 8的流来实现这个功能。假设你有两个包含对象的List,每个对象有一个属性,你想根据一个List中的属性值来过滤掉另一个List中不包含这个属性值的对象。下面是一种使用流的方式来实现这个功能 import java.util.ArrayList; import java.util…...
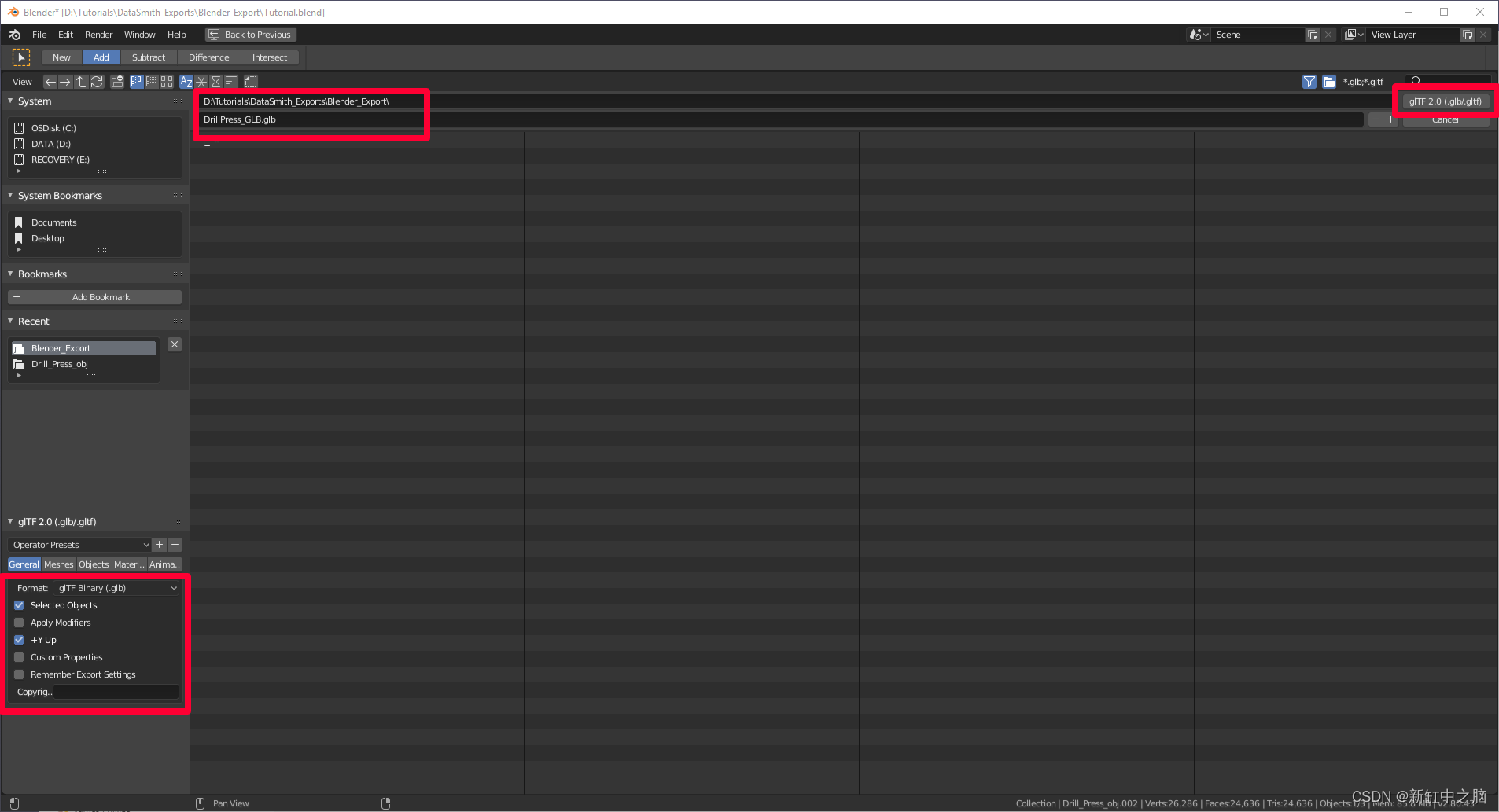
Blender 混合现实3D模型制作指南【XR】
本教程分步展示如何: 减少 3D 模型的多边形数量,使其满足 Microsoft Dynamics 365 Guides 和使用 Microsoft Power Apps 创建的应用程序中包含的混合现实组件的特定性能目标的性能需求。将 3D 模型的多种材质(颜色)组合成可应用于…...
)
kubeasz在线安装K8S集群单master集群(kubeasz安装之二)
一、介绍 Kubeasz 是一个基于 Ansible 自动化工具,用于快速部署和管理 Kubernetes 集群的工具。它支持快速部署高可用的 Kubernetes 集群,支持容器化部署,可以方便地扩展集群规模,支持多租户,提供了强大的监控和日志分…...

『C语言』数据在内存中的存储规则
前言 小羊近期已经将C语言初阶学习内容与铁汁们分享完成,接下来小羊会继续追更C语言进阶相关知识,小伙伴们坐好板凳,拿起笔开始上课啦~ 一、数据类型的介绍 我们目前已经学了基本的内置类型: char //字符数据类型 short …...
基于ssm+vue的新能源汽车在线租赁管理系统源码和论文PPT
基于ssmvue的新能源汽车在线租赁管理系统源码和论文PPT010 开发环境: 开发工具:idea 数据库mysql5.7(mysql5.7最佳) 数据库链接工具:navcat,小海豚等 开发技术:java ssm tomcat8.5 摘 要 随着科学技术的飞速发展࿰…...

深入解析IDS/IPS与SSL/TLS和网络安全
目录 防火墙 IDS IPS DMZ VPN VPS SSL/TLS 动态IP 静态IP 防火墙 防火墙是一种网络安全设备,用于监控和控制网络流量,保护网络免受未经授权的访问、恶意攻击和威胁。防火墙可以基于规则进行数据包过滤,允许或阻止特定类型的流量通过…...
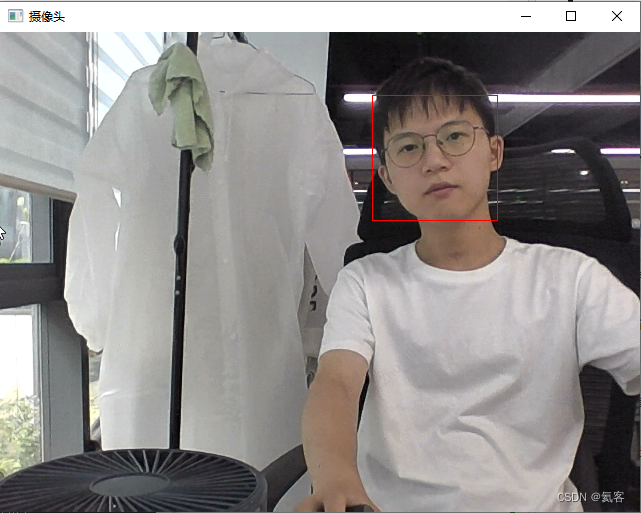
在Visual Studio上,使用OpenCV实现人脸识别
1. 环境与说明 本文介绍了如何在Visual Studio上,使用OpenCV来实现人脸识别的功能 环境说明 : 操作系统 : windows 10 64位Visual Studio版本 : Visual Studio Community 2022 (社区版)OpenCV版本 : OpenCV-4.8.0 (2023年7月最新版) 实现效果如图所示࿰…...
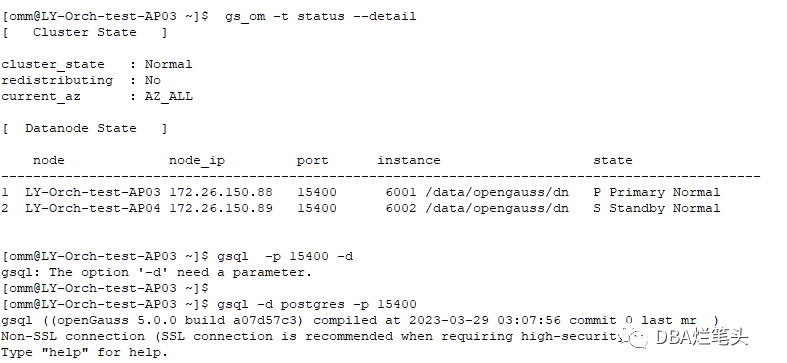
搭建openGauss 5.0 一主一从复制集群
openGauss是一款支持SQL2003标准语法,支持主备部署的高可用关系型国产数据库。 多种存储模式支持复合业务场景,新引入提供原地更新存储引擎。NUMA化数据结构支持高性能。Paxos一致性日志复制协议,主备模式,CRC校验支持高可用。支…...
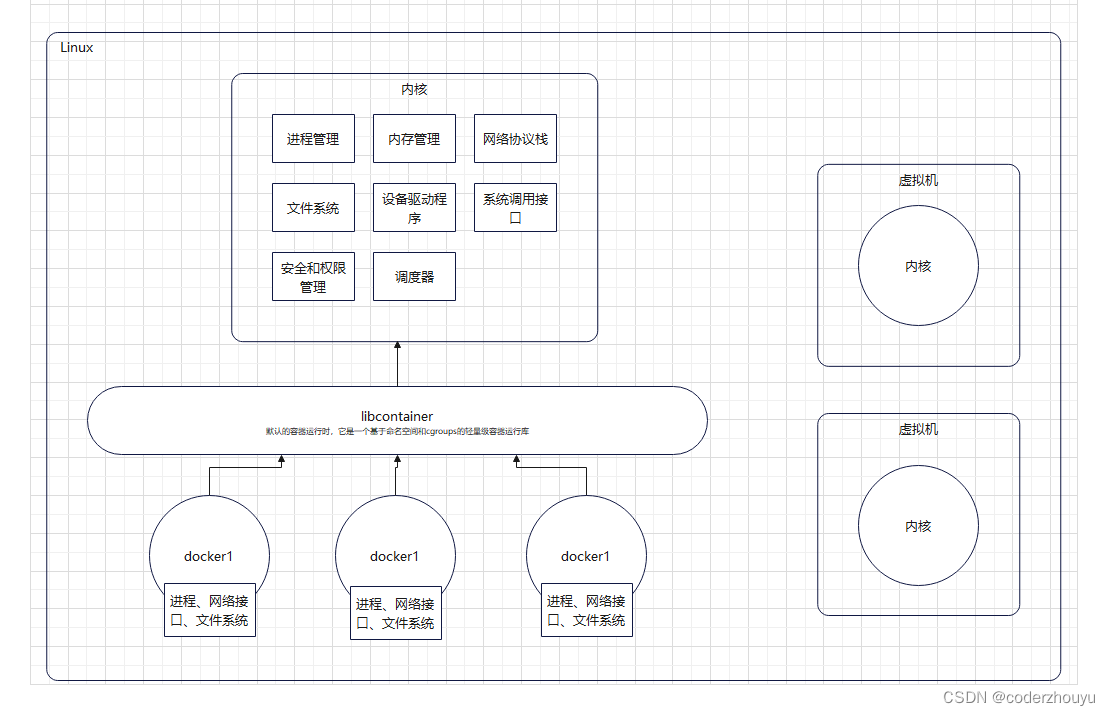
Docker碎碎念
docker和虚拟机的区别 虚拟机(VM)是通过在物理硬件上运行一个完整的操作系统来实现的。 每个虚拟机都有自己的内核、设备驱动程序和用户空间,它们是相互独立且完全隔离的。 虚拟机可以在不同的物理服务器之间迁移,因为它们是以整…...

【C++】extern
目录 1. 变量声明和定义的关系 2. 默认状态下,const对象仅在文件内有效 3. 链接指示:extern "C" 3.1 声明一个非C的函数 3.2 链接指示与头文件 3.3 指向extern "C"函数的指针 3.4 链接指示对整个声明都有效 3.5 导出C函数到…...
2023全网Mysql 合集(25w字)附课程 从安装到高级,实战
mysql学习 1.安装mysql 安装教程 2.mysql的详细学习教程 mysql的详细教程 3.mysql 的高级优化 MySQL高级篇(SQL优化、索引优化、锁机制、主从复制) 4.MySQL 面试 MySQL数据库面试题总结 二.mysql实战 一、创建数据表并插入数据 1、学生表 Stud…...
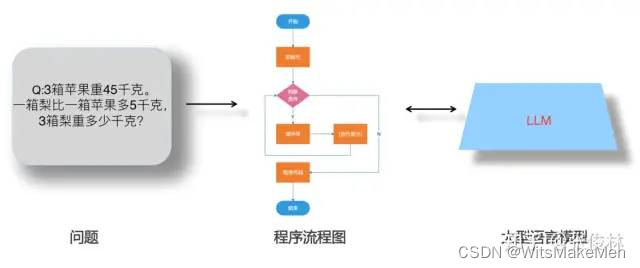
张俊林:由ChatGPT反思大语言模型(LLM)的技术精要
转自:https://mp.weixin.qq.com/s/eMrv15yOO0oYQ-o-wiuSyw 导读:ChatGPT出现后惊喜或惊醒了很多人。惊喜是因为没想到大型语言模型(LLM,Large Language Model)效果能好成这样;惊醒是顿悟到我们对LLM的认知及发展理念&a…...

单机编排docker compose
Docker之旅(8)-单机编排docker compose 当在宿主机启动较多的容器时候,如果都是手动操作会觉得比较麻烦而且容易出错, 并且每个容器之间也会有先后启动的顺序依赖等。这个时候推荐使用 docker 单机 编排工具 docker-compose,docker-compose …...

C++ 面向对象三大特性——多态
✅<1>主页:我的代码爱吃辣 📃<2>知识讲解:C 继承 ☂️<3>开发环境:Visual Studio 2022 💬<4>前言:面向对象三大特性的,封装,继承,多态ÿ…...

相同数字的积木游戏
题目描述 题目描述 小华和小薇一起通过玩积木游戏学习数学。 他们有很多积木,每个积木块上都有一个数字,积木块上的数字可能相同。 小华随机拿一些积木挨着排成一排,请小薇找到这排积木中数字相同目所处位置最远的2块积木块,计算…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
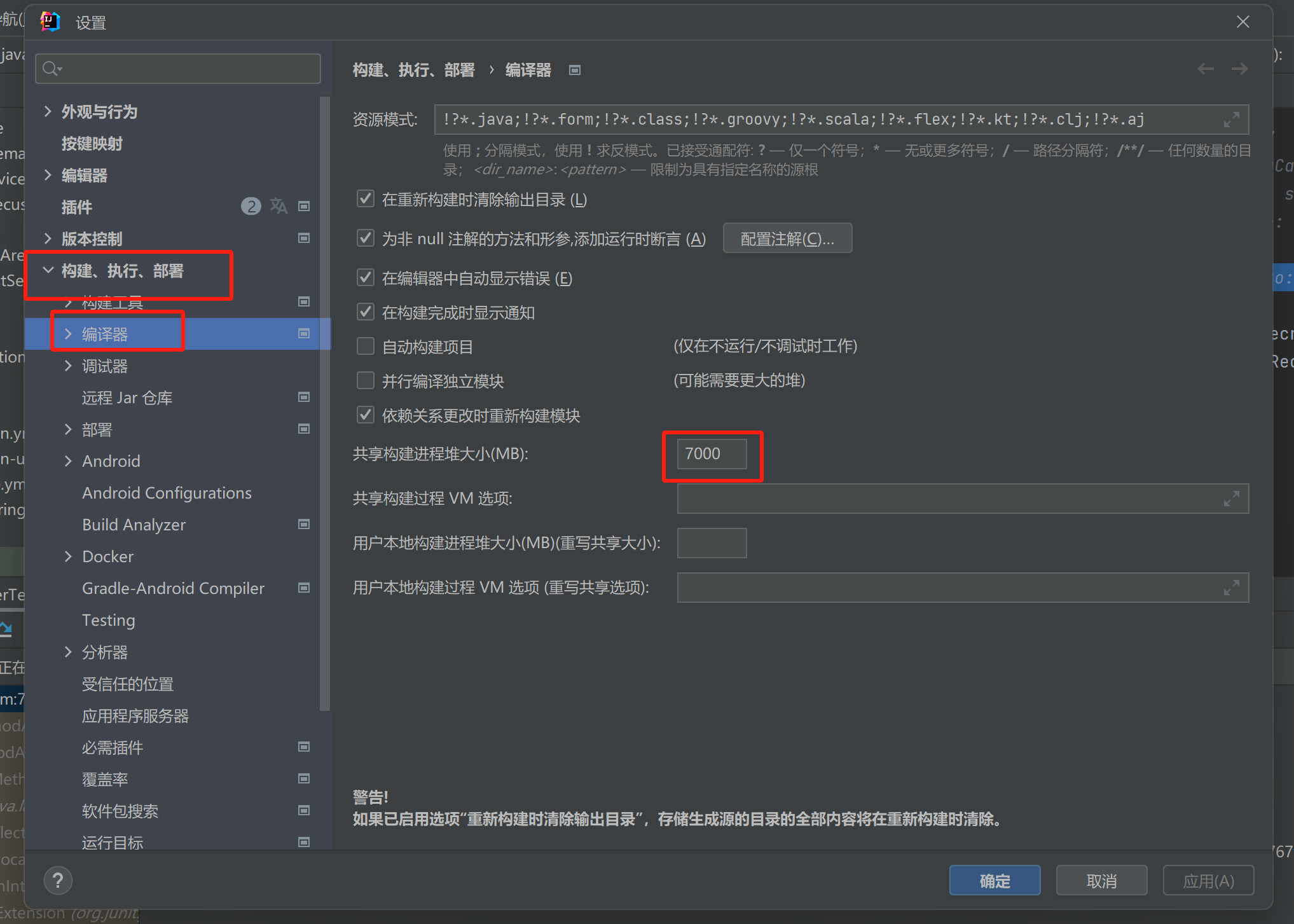
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...
