3D点云处理：点云聚类--FEC: Fast Euclidean Clustering for Point Cloud Segmentation
文章目录
- 聚类结果
- 一、论文内容
- 1.1 Ground Surface Removal
- 1.2 Fast Euclidean Clustering
- 题外：欧几里得聚类
- Fast Euclidean Clustering
- 二、参考
聚类结果
原始代码中采用的是pcl中的搜索方式，替换为另外第三方库，速度得到进一步提升。
一、论文内容
论文中给出的结论：该方法避免了在每个嵌套循环中不断遍历每个点是产生的耗时和内存，在经典分割方法的基础上实现了两个数量级，同时产生高质量的结果。
论文给出的方法包含两步：1. Ground Surface Removal;2.The Clustering of the remaining points;
1.1 Ground Surface Remo
相关文章：
3D点云处理：点云聚类--FEC: Fast Euclidean Clustering for Point Cloud Segmentation
文章目录 聚类结果一、论文内容1.1 Ground Surface Removal1.2 Fast Euclidean Clustering题外：欧几里得聚类Fast Euclidean Clustering二、参考聚类结果 原始代码中采用的是pcl中的搜索方式，替换为另外第三方库，速度得到进一步提升。 一、论文内容 论文中给出的结论：该…...
华为OD机试题 - 射击比赛（JavaScript）| 代码+思路+重要知识点
最近更新的博客 华为OD机试题 - 括号检查（JavaScript） 华为OD机试题 - 最小施肥机能效（JavaScript） 华为OD机试题 - 子序列长度（JavaScript） 华为OD机试题 - 众数和中位数（JavaScript） 华为OD机试题 - 服务依赖（JavaScript） 华为OD机试题 - 字符串加密（JavaScript）…...
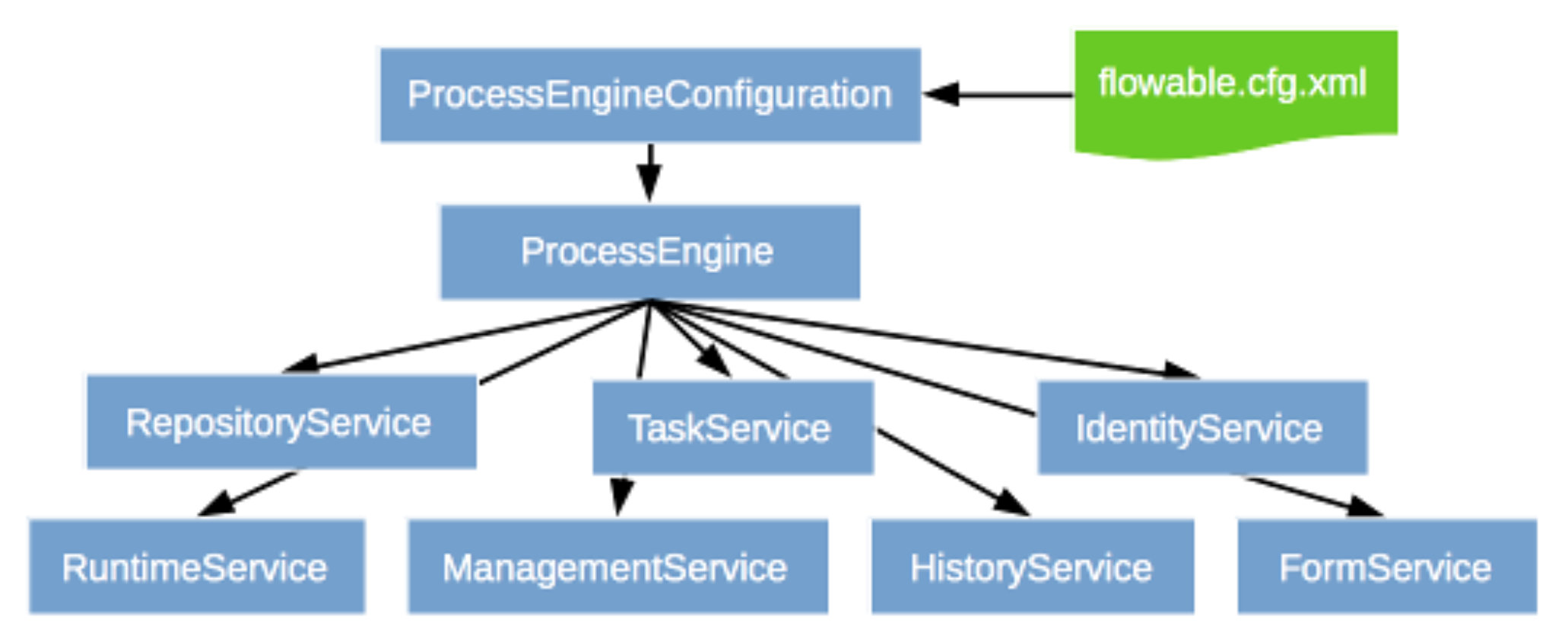
流程引擎之Flowable简介
背景Flowable 是一个流行的轻量级的采用 Java 开发的业务流程引擎，通过 Flowable 流程引擎，我们可以部署遵循 BPMN2.0 协议的流程定义（一般为XML文件）文件，并能创建流程实例，查询和访问流程相关的实例与数据…...
AcWing：4861. 构造数列、4862. 浇花(C++)
目录 4861. 构造数列 问题描述： 实现代码： 4862. 浇花 问题描述： 实现代码： 4861. 构造数列 问题描述： 我们规定如果一个正整数满足除最高位外其它所有数位均为 00，则称该正整数为圆数。 例如&…...
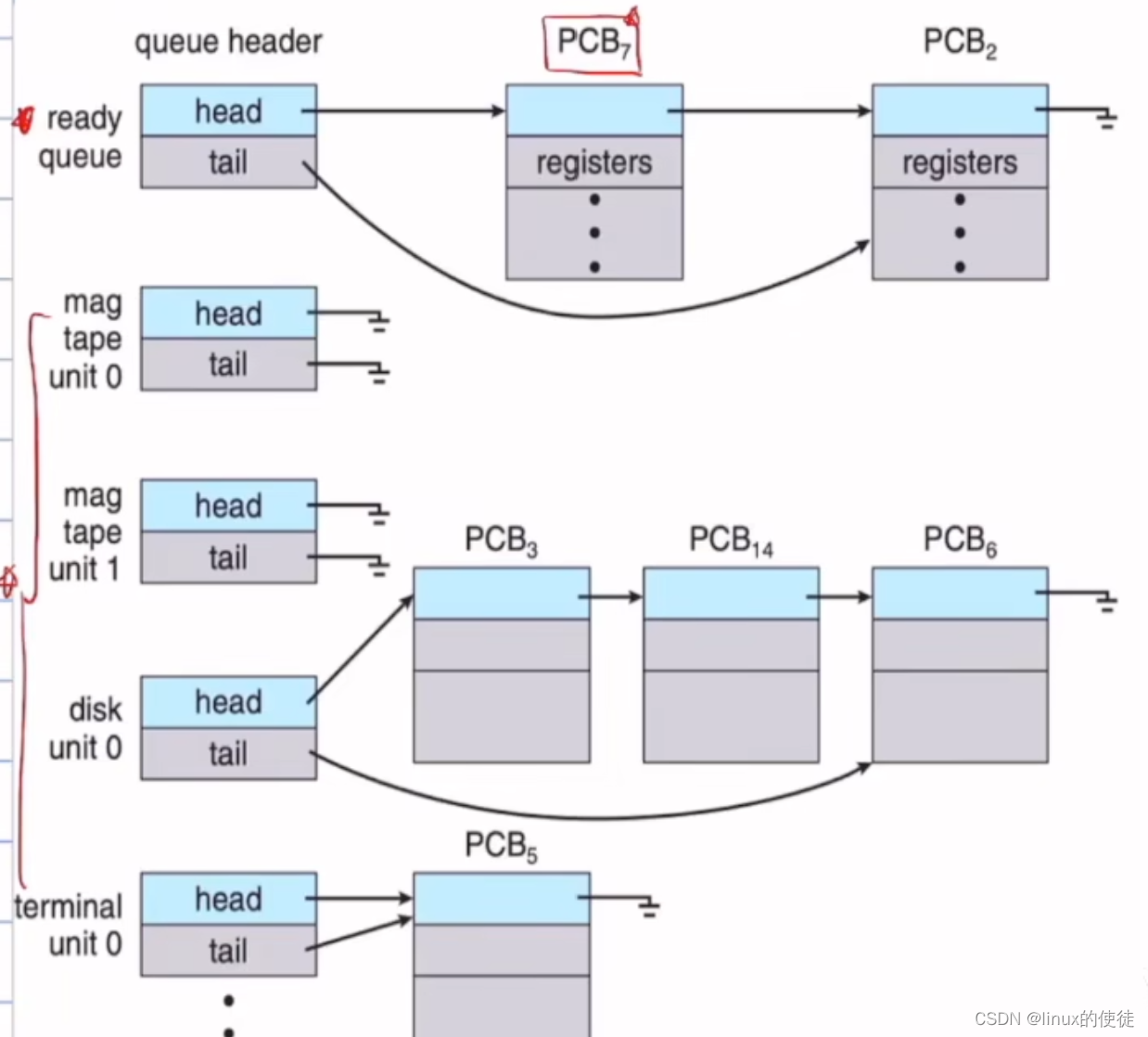
进程的概念
进程的概念 程序的概念 这里说的是一个可执行文件，passive的意思可以理解为我们这个执行文件需要我们进行双击才会被被执行。 双击后，程序入口地址读入寄存器，程序加载入主存，成为一个进程 进程是主动去获取想要的资源࿰…...
自动化测试5年经验，分享一些心得
自动化测试介绍 自动化测试(Automated Testing)，是指把以人为驱动的测试行为转化为机器执行的过程。实际上自动化测试往往通过一些测试工具或框架，编写自动化测试用例，来模拟手工测试过程。比如说，在项目迭代过程中，持…...
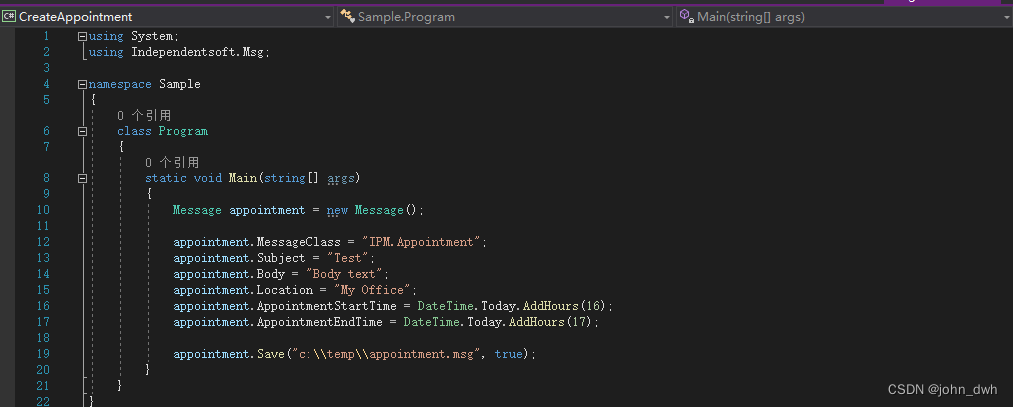
independentsoft.de/MSG .NET Framework Crack
MSG .NET 是用于 .NET Framework / .NET Core 的 Microsoft Outlook .msg 文件 API。API 允许您轻松创建/读取/解析/转换 .msg 文件等。API 不需要在机器上安装 Microsoft Outlook 或任何其他第三方应用程序或库即可工作。 以下示例向您展示了如何打开现有文件并显示消息的某些…...
基于Transformer的NLP处理管线
HuggingFace transformers 是一个整合了跨语言、视觉、音频和多模式模态与最先进的预训练模型并且提供用户友好的 API 的AI开发库。 它由 170 多个预训练模型组成，支持 PyTorch、TensorFlow 和 JAX 等框架，能够在代码之间进行互操作。 这个库还易于部署&…...
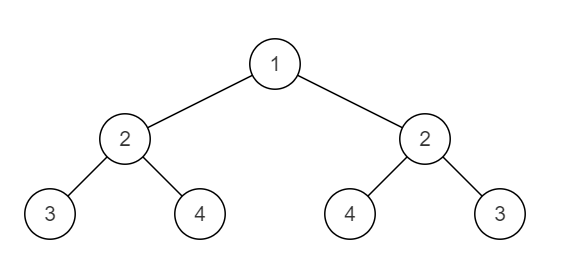
二叉树OJ（一）二叉树的最大深度 二叉搜索树与双向链表 对称的二叉树
二叉树的最大深度 二叉树中和为某一值的路径(一) 二叉搜索树与双向链表 对称的二叉树 二叉树的最大深度 描述 求给定二叉树的最大深度， 深度是指树的根节点到任一叶子节点路径上节点的数量。 最大深度是所有叶子节点的深度的最大值。 （注：…...
使用Fairseq进行Bart预训练
文章目录前言环境流程介绍数据部分分词部分预处理部分训练部分遇到的问题问题1可能遇到的问题问题1问题2前言 本文是使用 fairseq 做 Bart 预训练任务的踩坑记录huggingface没有提供 Bart 预训练的代码 facebookresearch/fairseq: Facebook AI Research Sequence-to-Sequence…...
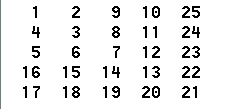
n阶数字回转方阵 ← 模拟法
【问题描述】 请编程输出如下数字回旋方阵。 【算法代码】 #include <bits/stdc.h> using namespace std;const int maxn100; int z[maxn][maxn];void matrix(int n) {int num2;z[0][0]1;int i0,j1;while(i<n && j<n) {while(i<j) z[i][j]num;while(j&…...
【人工智能AI】二、NoSQL 基础知识《NoSQL 企业级基础入门与进阶实战》
写一篇介绍 NoSQL 基础知识的技术文章，分5个章节，每个章节细分到3级目录，重点介绍一下NoSQL 数据模型，NoSQL 数据库架构，NoSQL 数据库特性等，不少于2000字。 NoSQL 基础知识 NoSQL（Not Only SQ…...
Camera Rolling Shutter和Global Shutter的区别
卷帘快门（Rolling Shutter）与全局快门（Global Shutter）的区别 什么是快门 快门是照相机用来控制感光片有效曝光时间的机构。 快门是照相机的一个重要组成部分，它的结构、形式及功能是衡量照相机档次的一个重要因素。 …...
模版之AnyType
title: 模版之AnyType date: 2023-02-19 21:49:53 permalink: /pages/54a0bf/ categories: 通用领域编程语言C tags:C元编程 author: name: zhengzhibing link: https://azmddy.top/pages/54a0bf/ 模版之AnyType 在研究C的编译期反射时，发现了AnyType很有意思。 首…...
【汇编】一、环境搭建（一只 Assember 的成长史）
嗨~你好呀！ 我是一名初二学生，热爱计算机，码龄两年。最近开始学习汇编，希望通过 Blog 的形式记录下自己的学习过程，也和更多人分享。 这篇文章主要讲述汇编环境的搭建过程。 话不多说~我们开始吧！ 系统环…...
【博客628】k8s pod访问集群外域名原理以及主机开启了systemd-resolved的不同情况
k8s pod访问集群外域名原理以及使用了systemd-resolved的不同情况 1、不同情况下的linux主机访问外部域名原理 没有使用systemd-resolved的linux主机上访问外部域名一般是按照以下步骤来的： 从dns缓存里查找域名与ip的映射关系 从/etc/hosts里查找域名与ip的映射…...
测试3.测试方法的分类
3.测试分类 系统测试包括回归测试和冒烟测试 回归测试：修改了旧的代码后，重新测试功能是否正确，有没有引入新的错误或导致其它代码产生错误 冒烟测试：目的是确认软件基本功能正常，可以进行后续的正式测试工作 按是否…...
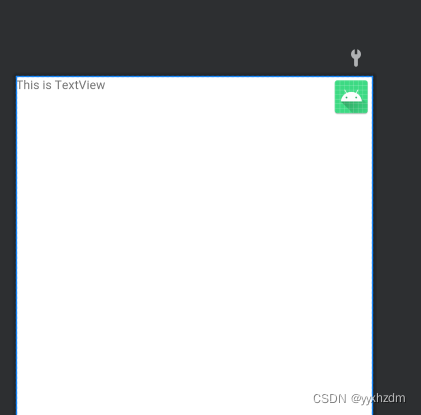
Android 基础知识4-2.9 FrameLayout（帧布局）详解
一、FrameLayout（帧布局）概述 FrameLayout又称作帧布局，它相比于LinearLayout和RelativeLayout要简单很多，因为它的应用场景也少了很多。这种布局没有方便的定位方式，所有的控件都会默认摆放在布局的左上角。 示例1代…...
Go语言xorm框架
xorm xorm是一个简单而强大的Go语言ORM库通过它可以使数据库操作非常简便。 官网: https://xorm.io/ 中文文档: https://gitea.com/xorm/xorm/src/branch/master/README_CN.md 特性 支持 Struct 和数据库表之间的灵活映射，并支持自动同步事务支持同时支持原始SQL…...
19_微信小程序之优雅实现侧滑菜单
19_微信小程序之优雅实现侧滑菜单一.先上效果图 要实现这样一个效果，布局其实很简单，整体布局是一个横向滚动的scroll-view，难点在于怎么控制侧滑菜单的回弹，以及寻找回弹的边界条件? 此篇文章主要是基于uni-app来实现的…...
vscode里如何用git
打开vs终端执行如下： 1 初始化 Git 仓库（如果尚未初始化） git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程：（白话解释） 我们将原始待发送的消息称为 M M M，依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)（意思就是 G （ x ) G（x) G（x) 是已知的）࿰…...
基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施，由雇主和个人按一定比例缴纳保险费，建立社会医疗保险基金，支付雇员医疗费用的一种医疗保险制度， 它是促进社会文明和进步的…...
CMake基础：构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
【机器视觉】单目测距——运动结构恢复
ps：图是随便找的，为了凑个封面 前言 在前面对光流法进行进一步改进，希望将2D光流推广至3D场景流时，发现2D转3D过程中存在尺度歧义问题，需要补全摄像头拍摄图像中缺失的深度信息，否则解空间不收敛…...
MVC 数据库
MVC 数据库 引言 在软件开发领域，Model-View-Controller（MVC）是一种流行的软件架构模式，它将应用程序分为三个核心组件：模型（Model）、视图（View）和控制器（Controller）。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系，以…...
跨链模式：多链互操作架构与性能扩展方案
跨链模式：多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈：模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展（H2Cross架构）： 适配层…...
反射获取方法和属性
Java反射获取方法 在Java中，反射（Reflection）是一种强大的机制，允许程序在运行时访问和操作类的内部属性和方法。通过反射，可以动态地创建对象、调用方法、改变属性值，这在很多Java框架中如Spring和Hiberna…...
微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数（函数作为参数、返回值） 三、匿名函数与闭包1. 匿名函数（Lambda函…...