第 7 章 排序算法(1)
7.1排序算法的介绍
排序也称排序算法(Sort Algorithm),排序是将一组数据,依指定的顺序进行排列的过程。
7.2排序的分类:
- 内部排序:
指将需要处理的所有数据都加载到**内部存储器(内存)**中进行排序。 - 外部排序法:
数据量过大,无法全部加载到内存中,需要借助**外部存储(文件等)**进行排序。 - 常见的排序算法分类(见右图):
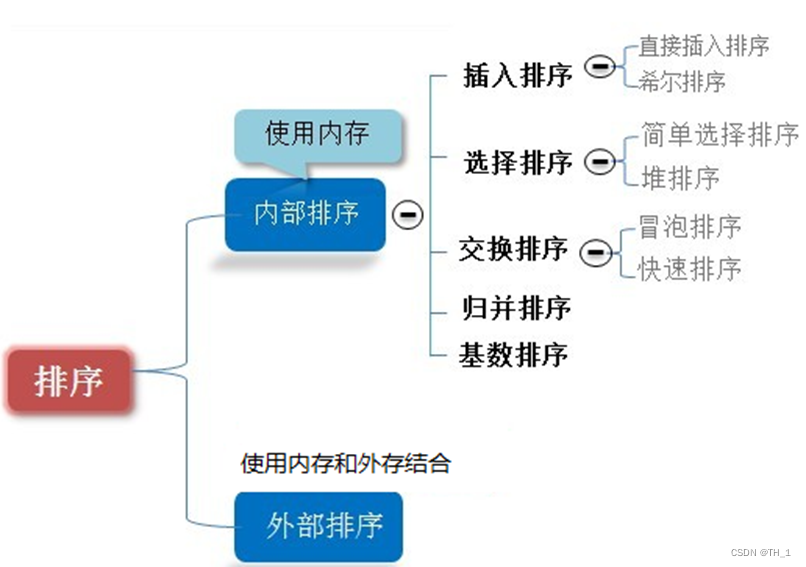
7.3算法的时间复杂度
7.3.1度量一个程序(算法)执行时间的两种方法
-
事后统计的方法这种方法可行, 但是有两个问题:一是要想对设计的算法的运行性能进行评测,需要实际运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素, 这种方式,要在同一台计算机的相同状态下运行,才能比较那个算法速度更快。
-
事前估算的方法
通过分析某个算法的时间复杂度来判断哪个算法更优.
7.3.2时间频度
基本介绍
时间频度:一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。
一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。[举例说明]
举例说明-基本案例
比如计算1-100所有数字之和, 我们设计两种算法:
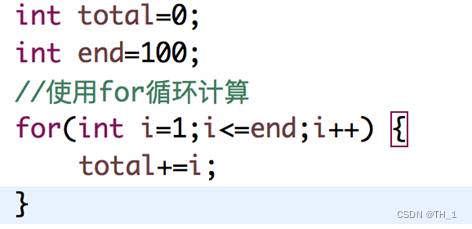

举例说明-忽略常数项
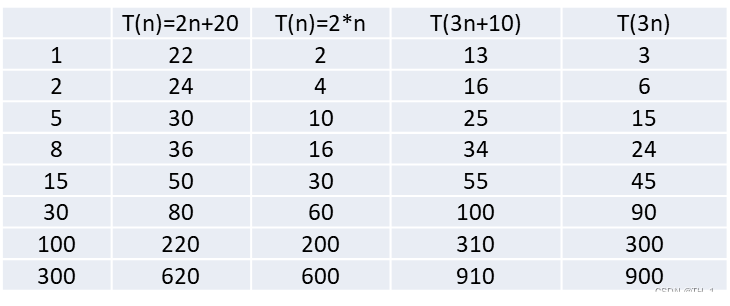
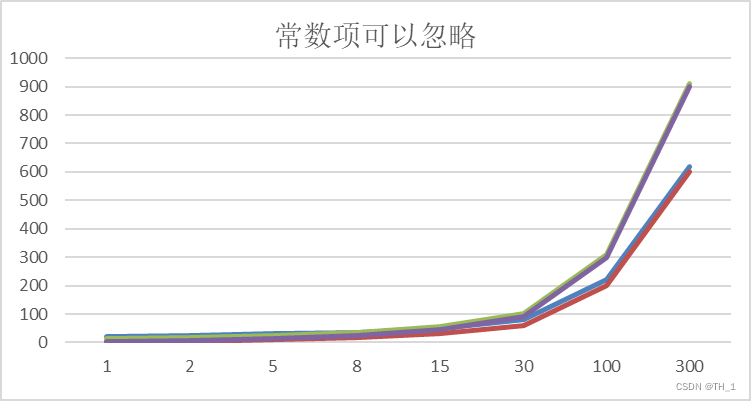
结论:
2n+20 和 2n 随着n 变大,执行曲线无限接近, 20可以忽略
3n+10 和 3n 随着n 变大,执行曲线无限接近, 10可以忽略
举例说明-忽略低次项
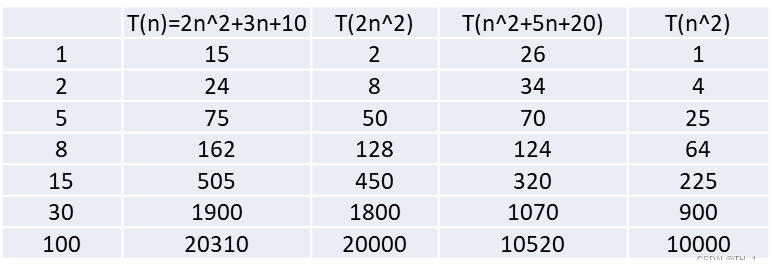
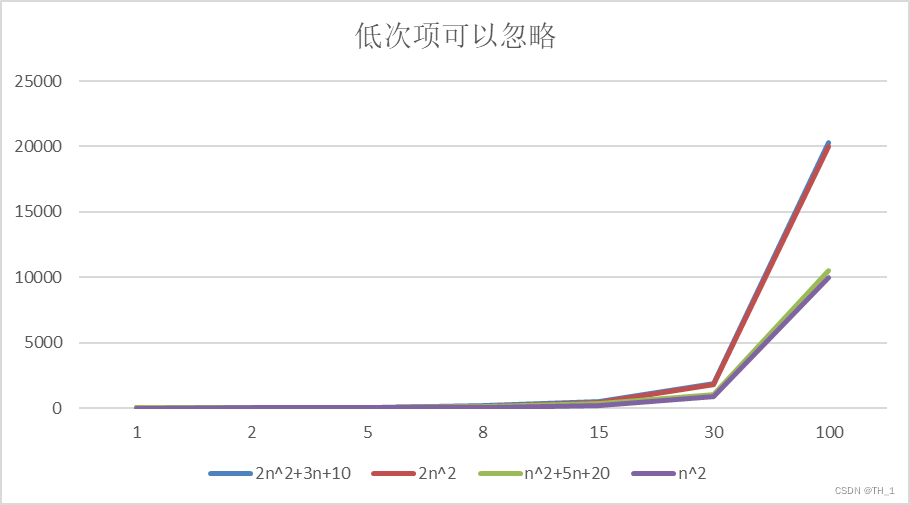
结论:
2n^2+3n+10 和 2n^2 随着n 变大, 执行曲线无限接近, 可以忽略 3n+10
n^2+5n+20 和 n^2 随着n 变大,执行曲线无限接近, 可以忽略 5n+20
举例说明-忽略系数
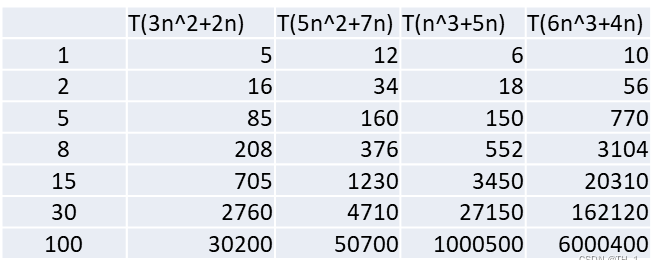
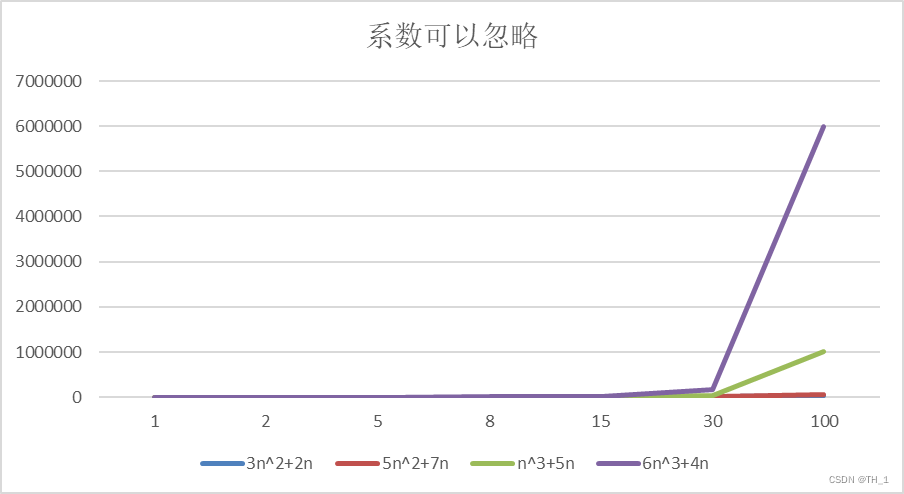
结论:
随着n值变大,5n^2+7n 和 3n^2 + 2n ,执行曲线重合, 说明 这种情况下, 5和3可以忽略。
而n^3+5n 和 6n^3+4n ,执行曲线分离,说明多少次方式关键
7.3.3时间复杂度
-
一般情况下,算法中的基本操作语句的重复执行次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n) / f(n) 的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作 T(n)=O( f(n) ),称O( f(n) ) 为算法的渐进时间复杂度,简称时间复杂度。
-
T(n) 不同,但时间复杂度可能相同。 如:T(n)=n²+7n+6 与 T(n)=3n²+2n+2 它们的T(n) 不同,但时间复杂度相同,都为O(n²)。
-
计算时间复杂度的方法:
- 用常数1代替运行时间中的所有加法常数 T(n)=n²+7n+6 => T(n)=n²+7n+1
- 修改后的运行次数函数中,只保留最高阶项 T(n)=n²+7n+1 => T(n) = n²
- 去除最高阶项的系数 T(n) = n² => T(n) = n² => O(n²)
7.3.4常见的时间复杂度
- 常数阶O(1)
- 对数阶O(log2n)
- 线性阶O(n)
- 线性对数阶O(nlog2n)
- 平方阶O(n^2)
- 立方阶O(n^3)
- k次方阶O(n^k)
- 指数阶O(2^n)
常见的时间复杂度对应的图:
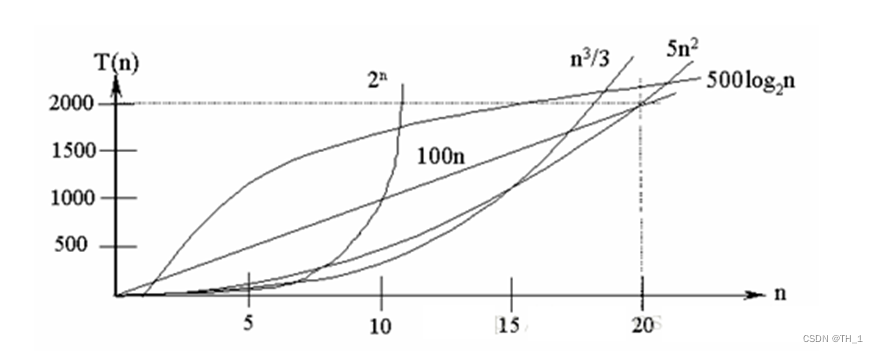
说明:
- 常见的算法时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)< Ο(nk) <Ο(2n) ,随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低
- 从图中可见,我们应该尽可能避免使用指数阶的算法
1) 常数阶O(1)
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)
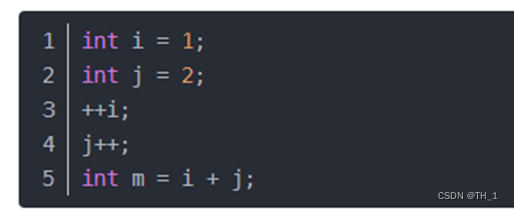
上述代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
2) 对数阶O(log2n)
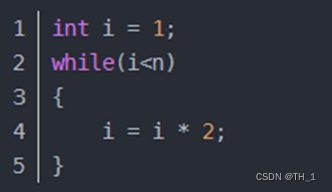
说明:在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2n也就是说当循环 log2n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(log2n) 。 O(log2n) 的这个2 时间上是根据代码变化的,i = i * 3 ,则是 O(log3n) .

3) 线性阶O(n)
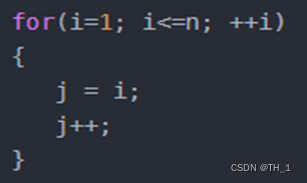
说明:这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度
4) 线性对数阶O(nlogN)

说明:线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)
5) 平方阶O(n²)
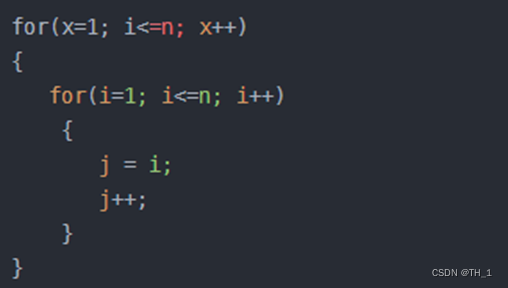
说明:平方阶O(n²) 就更容易理解了,如果把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²),这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O(nn),即 O(n²) 如果将其中一层循环的n改成m,那它的时间复杂度就变成了 O(mn)
6) 立方阶O(n³)、K次方阶O(n^k)
说明:参考上面的O(n²) 去理解就好了,O(n³)相当于三层n循环,其它的类似
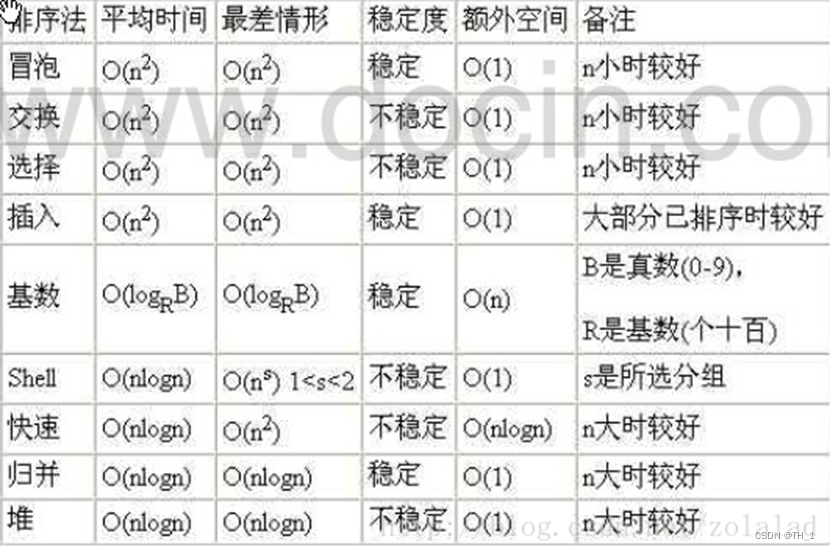
7.3.5平均时间复杂度和最坏时间复杂度
- 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下,该算法的运行时间。
- 最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度均是最坏情况下的时间复杂度。 这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限,这就保证了算法的运行时间不会比最坏情况更长。
- 平均时间复杂度和最坏时间复杂度是否一致,和算法有关(如图:)。
7.4算法的空间复杂度简介
7.4.1基本介绍
- 类似于时间复杂度的讨论,一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间,它也是问题规模n的函数。
- 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元,例如快速排序和归并排序算法,基数排序就属于这种情况
- 在做算法分析时,主要讨论的是时间复杂度。从用户使用体验上看,更看重的程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间.
相关文章:

第 7 章 排序算法(1)
7.1排序算法的介绍 排序也称排序算法(Sort Algorithm),排序是将一组数据,依指定的顺序进行排列的过程。 7.2排序的分类: 内部排序: 指将需要处理的所有数据都加载到**内部存储器(内存)**中进行排序。外部排序法: 数据量过大&am…...
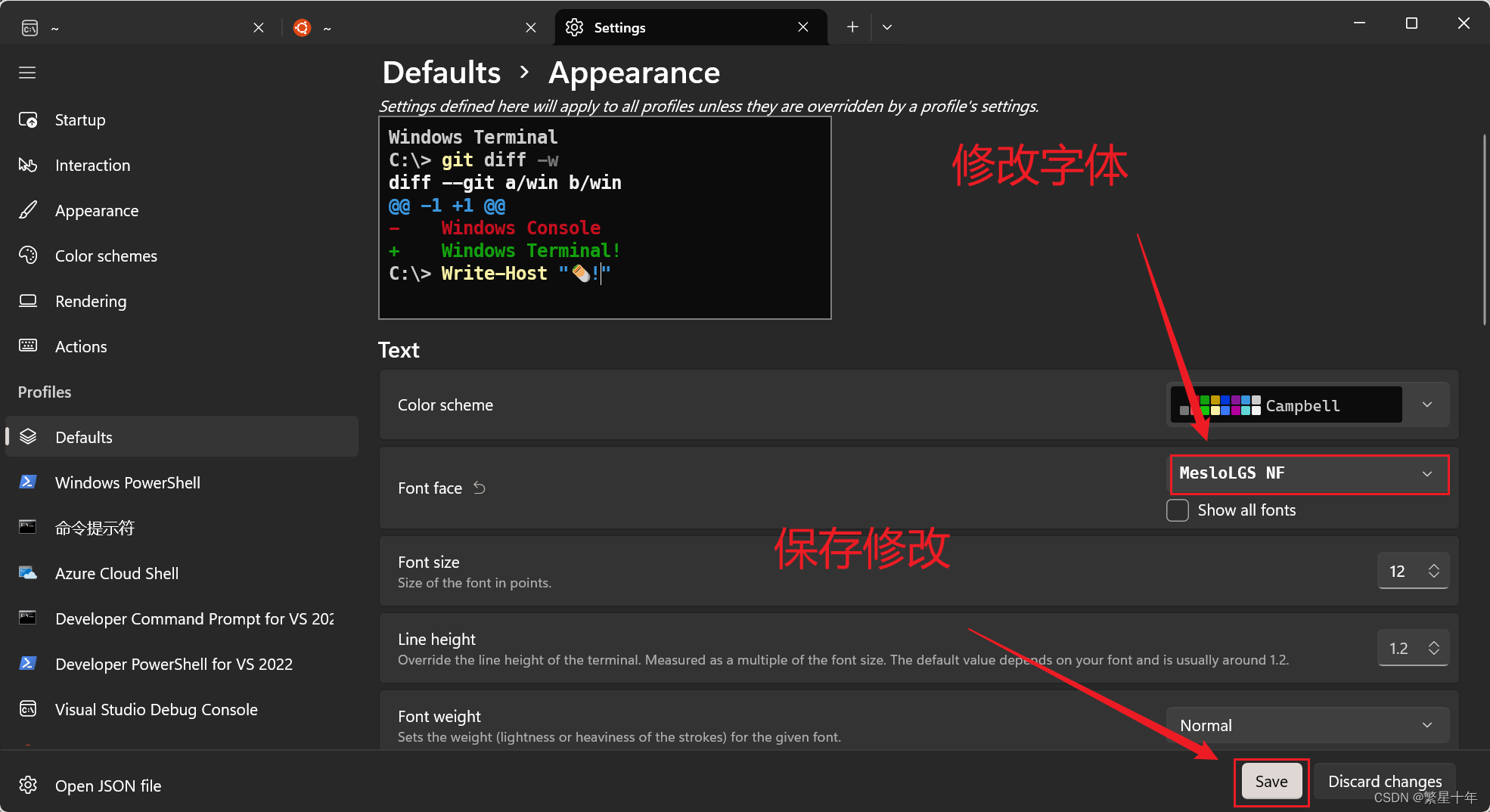
wsl,字体乱码问题
配置wsl,字体乱码问题 一、前言 用zsh配置好wsl,每次打开还是会出现乱码,只有再新打开一个终端才会显示字体 如下图:第一次打开,出现乱码 如图:按加号,再开一个新终端才会显示字体。 二、解…...

【NetCore】10-路由定义
文章目录 路由与终结点:如何规划好Web Api1. 路由1.1 路由映射1.2 路由注册方式1.3 路由约束总结: Web Api定义 路由与终结点:如何规划好Web Api 1. 路由 1.1 路由映射 路由系统核心作用是指URL和应用程序Controller的对应关系的一种映射 这种映射的作…...
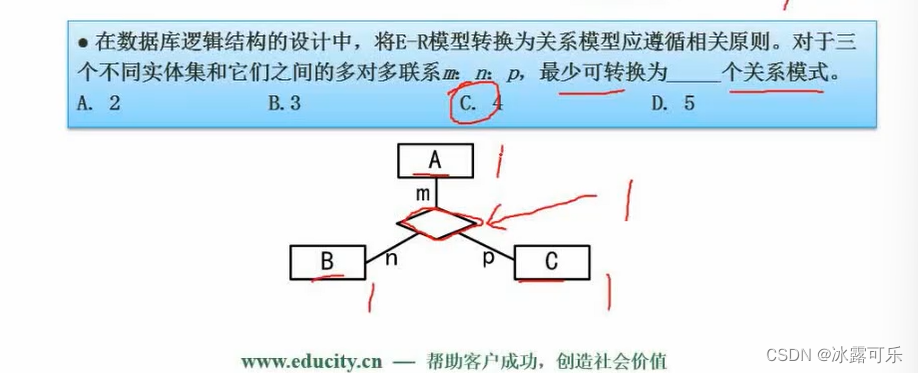
软考:中级软件设计师:数据库模式、ER模型
软考:中级软件设计师:数据库模式、ER模型 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准…...
海量数据迁移,亚马逊云科技云数据库服务为大库治理提供新思路
1.背景 目前,文档型数据库由于灵活的schema和接近关系型数据库的访问特点,被广泛应用,尤其是游戏、互联网金融等行业的客户使用MongoDB构建了大量应用程序,比如游戏客户用来处理玩家的属性信息;又如股票APP用来存储与时…...
DevOps系列文章之 GitlabCICD自动化部署SpringBoot项目
一、概述 本文主要记录如何通过Gitlab CI/CD自动部署SpringBoot项目jar包。 二、前期准备 准备三台 CentOS7服务器,分别部署以下服务: 序号系统IP服务1CentOS7192.168.56.10Gitlab2CentOS7192.168.56.11Runner (安装Docker)3Cen…...
汽车租赁管理系统/汽车租赁网站的设计与实现
摘 要 租赁汽车走进社区,走进生活,成为当今生活中不可缺少的一部分。随着汽车租赁业的发展,加强管理和规范管理司促进汽车租赁业健康发展的重要推动力。汽车租赁业为道路运输车辆一种新的融资服务形式、广大人民群众一种新的出行消费方式和…...
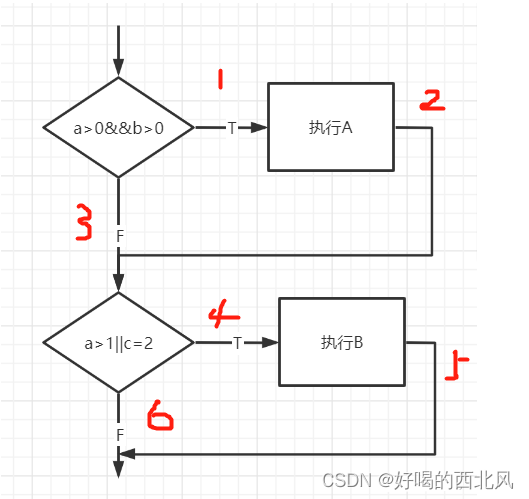
语句覆盖、条件覆盖、判定覆盖、条件-判定覆盖、路径覆盖
白盒测试是结构测试,主要对代码的逻辑进行验证。 逻辑覆盖率:语句覆盖<条件覆盖<判定覆盖<条件-判定覆盖<组合覆盖<路径覆盖 例子 一、语句覆盖 最基础的覆盖,只要每一个执行处理框内的语句都能执行就可,不用关注…...

二进制逻辑运算符
运算的优先级:非>与>或 1.逻辑与:“ ∧ \wedge ∧“,“ ⋅ \cdot ⋅“,and 在逻辑问题中与是所有的都是真结果才是真,比如: 1010101011 1010101011 1010101011和 1010110010 1010110010 1010110010…...

Bug日记-webstorm运行yarn 命令报错
在windows中输入yarn -v正确输出,在webstrom终端中运行yarn命令输出错误 问题:可能是由于 WebStorm 配置问题导致的。 解决方案: 检查 WebStorm 的终端配置:在 WebStorm 中,点击菜单栏的 “File”(文件&am…...
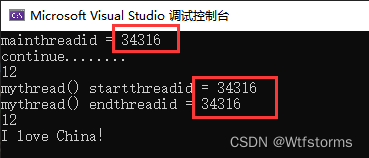
C++11并发与多线程笔记(9) async、future、packaged_task、promise
C11并发与多线程笔记(9) async、future、packaged_task、promise 1、std::async、std::future创建后台任务并返回值2、std::packaged_task:打包任务,把任务包装起来3、std::promise3、小结 1、std::async、std::future创建后台任务…...
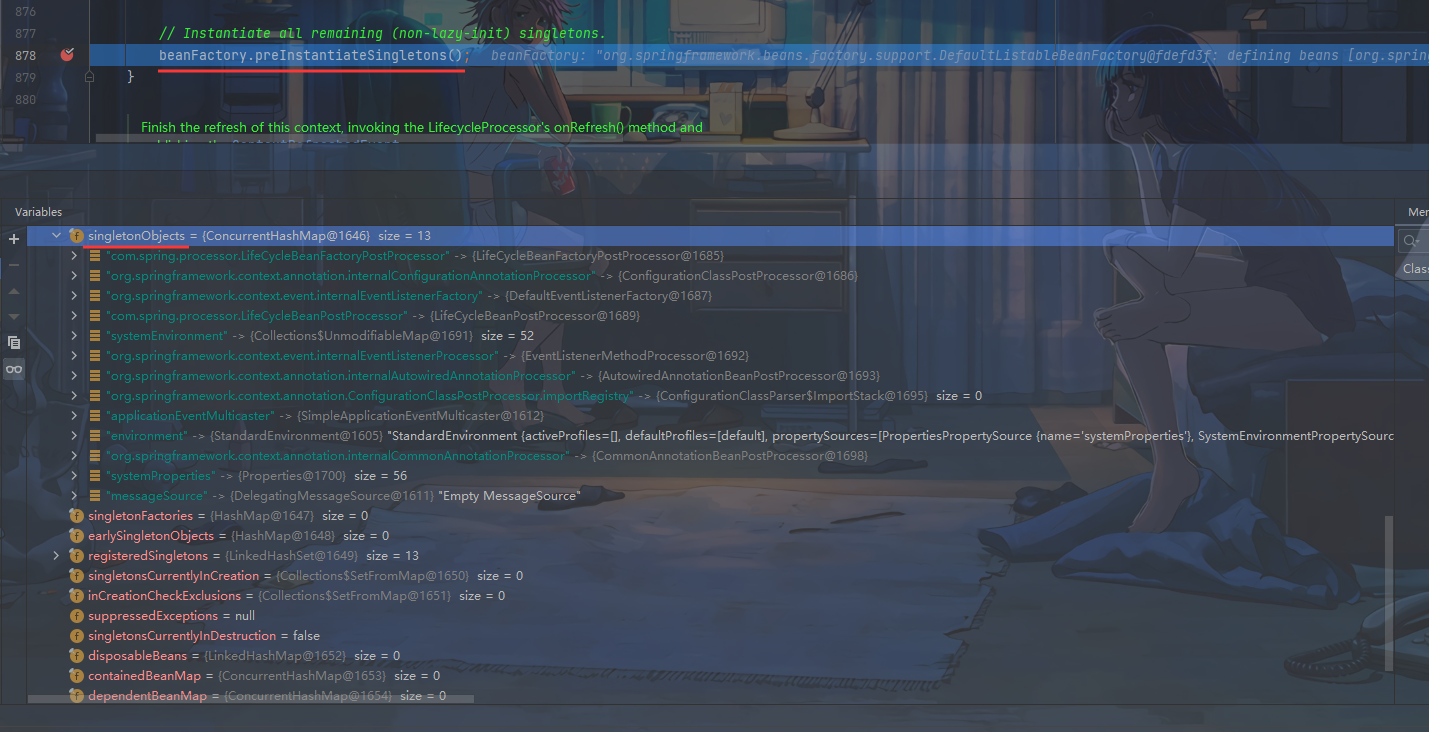
Mr. Cappuccino的第63杯咖啡——Spring之AnnotationConfigApplicationContext源码分析
Spring之AnnotationConfigApplicationContext源码分析 源码分析 源码分析 以上一篇文章《Spring之Bean的生命周期》的代码进行源码分析 AnnotationConfigApplicationContext applicationContext new AnnotationConfigApplicationContext(SpringConfig02.class); LifeCycleBe…...
opencv直方图与模板匹配
import cv2 #opencv读取的格式是BGR import numpy as np import matplotlib.pyplot as plt#Matplotlib是RGB %matplotlib inline def cv_show(img,name):cv2.imshow(name,img)cv2.waitKey()cv2.destroyAllWindows() 直方图 cv2.calcHist(images,channels,mask,histSize,ran…...

Apache Doris 入门教程31:计算节点
需求场景 目前Doris是一个典型Share-Nothing的架构, 通过绑定数据和计算资源在同一个节点获得非常好的性能表现. 但随着Doris计算引擎性能持续提高, 越来越多的用户也开始选择使用Doris直接查询数据湖数据. 这类场景是一种Share-Disk场景, 数据往往存储在远端的HDFS/S3上, 计…...
Nacos和GateWay路由转发NotFoundException: 503 SERVICE_UNAVAILABLE “Unable to find
问题再现: 2023-08-15 16:51:16,151 DEBUG [reactor-http-nio-2][CompositeLog.java:147] - [dc73b32c-1] Encoding [{timestampTue Aug 15 16:51:16 CST 2023, path/content/course/list, status503, errorService Unavai (truncated)...] 2023-08-15 16:51:16,17…...
)
2021年9月全国计算机等级考试真题(二级C语言)
2021年9月全国计算机等级考试真题(二级C语言) 第1题 下列叙述中正确的是( )。 A. 算法的复杂度是指算法所处理的数据量 B. 算法的复杂度是指算法程序中指令的数量 C. 算法的复杂度是指算法控制结构的复杂程度 D. 算法的复杂度包…...
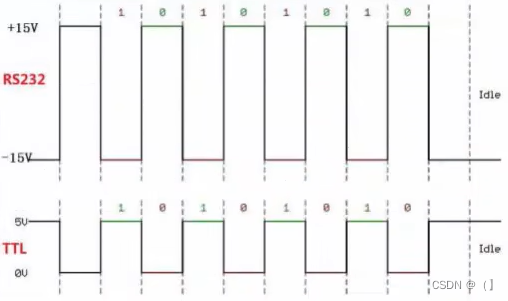
串口通讯
USART是全双工同步通讯 在同步通信中,数据信号所传输的内容绝大多数属于有效数据,而异步通信中包含了各种帧的标识符,所以同步通讯的效率更高。但是同步通信对时钟要求苛刻,允许的误差小。而异步通信则允许双方的误差较大 比特率…...

自动拉取 GitHub 仓库更新的脚本
更好的阅读体验 \huge{\color{red}{更好的阅读体验}} 更好的阅读体验 由于将 HAUE-CS-WIKI 部署到了我自己的服务器上作为国内镜像站,每次在源站更新后都需要手动拉取镜像站的更新实在是太麻烦了,因此产生了编写该脚本的需求( 读者可根据该…...
如何获得Android 14复活节彩蛋
每个新的安卓版本都有隐藏复活节彩蛋的悠久传统,可以追溯到以前,每个版本都以某种甜食命名。安卓14也不例外,但这一次的主题都是围绕太空构建的——还有一个复活节彩蛋。 安卓14复活节彩蛋实际上是一款很酷的小迷你游戏,你可以乘…...
国产32位单片机XL32F001,带1 路 12bit ADC,I2C、SPI、USART 等外设
XL32F001 系列单片机采用高性能的 32 位 ARM Cortex-M0内核,宽电压工作范围的 MCU。嵌入 24KbytesFlash 和 3Kbytes SRAM 存储器,最高工作频率 24MHz。包含多种不同封装类型多款产品。芯片集成 I2C、SPI、USART 等通讯外设,1 路 12bit ADC&am…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...
