Python上楼梯问题:递归解法探究(斐波那契变种)(记忆化递归)
文章目录
- 上楼梯问题:递归解法探究
- 问题定义
- 解决方案
- 1. 递归
- 2. 记忆化递归
- 关于python memo={}默认参数和字典的语法
- 语法功能
- 版本信息
- 注意事项
- 结论
上楼梯问题:递归解法探究
在这篇文章中,将对上楼梯问题进行深入探讨。上楼梯问题是一种常见的计算机科学问题,通常用于研究和理解动态规划、递归和记忆化等关键编程概念。首先,让我们更好地理解问题本身。
问题定义
给定一个楼梯,假设它有n个台阶。每次可以选择爬一阶、两阶或三阶。问题是,存在多少种可能的方式来爬到楼梯顶部?
这个问题在数学中被称为斐波那契变种,因为其解决方案包含了类似的递归结构。
解决方案
1. 递归
最直接的方法是使用递归。基本思想是每次爬楼梯都有三种选择,然后递归地求解剩余的台阶数。
def climbStairs(n):if n <= 0:return 0elif n == 1:return 1elif n == 2:return 2elif n == 3:return 4else:return climbStairs(n-1) + climbStairs(n-2) + climbStairs(n-3)
解释:因为每次爬楼梯都有三种选择,所以对于n阶楼梯,可以选择先走1阶,可以选择先走2阶,也可以选择先走3阶,那么求解爬n阶楼梯的方式数量就变成了:求解爬(n-1)阶楼梯的方式数量 + 爬(n-2)阶楼梯的方式数量 + 爬(n-3)阶楼梯的方式数量。
以上代码的缺点是运行时间会随着n的增大而呈指数增长,因为存在大量的重复计算。例如,climbStairs(n-1)和climbStairs(n-2)中都计算了climbStairs(n-3)。

2. 记忆化递归
为了避免重复计算,可以使用一种叫做"记忆化"的技术,即保存已经计算过的结果,当需要再次计算时,就直接从存储空间取出结果。
def climbStairs(n, memo={}):if n <= 0:return 0elif n == 1:return 1elif n == 2:return 2elif n == 3:return 4elif n not in memo:memo[n] = climbStairs(n-1) + climbStairs(n-2) + climbStairs(n-3)return memo[n]
此代码将以前计算的值存储在名为"memo"的字典中。如果需要计算的值已经在"memo"中,则直接返回该值,否则进行计算并将结果存入"memo"。
关于python memo={}默认参数和字典的语法
在Python中,memo={}是一种使用字典(dictionary)的方式来存储已经计算过的值,这样可以在以后需要这些值时快速获取,避免了重复计算。这种技术被称为"记忆化"(Memoization)。

语法功能
memo={}这部分代码创建了一个空的字典,名为memo。在函数climbStairs的参数列表中,将memo初始化为空字典。这样,当首次调用函数时,如果没有传入memo参数,那么就会创建一个新的空字典。
之后,在函数体中,当需要计算爬n个台阶的方法数时,先检查memo字典中是否已经有这个结果。如果有,就直接从字典中取出结果并返回;如果没有,就进行计算,并把结果存入memo字典,以备后续使用。
elif n not in memo:memo[n] = climbStairs(n-1) + climbStairs(n-2) + climbStairs(n-3)
return memo[n]
版本信息
这种默认参数和字典的使用方式在Python的早期版本中就已经存在。至少在Python 2.0中就已经支持,而这个版本于2000年发布。所以,可以说这是一个相当成熟的Python功能。

注意事项
需要注意的是,虽然这里memo作为默认参数被初始化为空字典,但由于Python默认参数的特性,即它们只会在函数定义的时候被初始化一次,所以在多次调用函数时,这个memo字典实际上是被共享的。这正好符合我们的需求,因为我们希望在多次递归调用中共享这个memo字典,以达到记忆化的目的。

结论
上楼梯问题提供了一个很好的框架,可以用来学习和理解递归和记忆化等编程技术。尽管这个问题看起来简单,但实际上包含了许多关键的计算机科学概念。
引用:
- “Programming Interviews Exposed: Secrets to Landing Your Next Job” by John Mongan et al.
- “Cracking the Coding Interview: 189 Programming Questions and Solutions” by Gayle Laakmann McDowell
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ ᅟᅠ
相关文章:

Python上楼梯问题:递归解法探究(斐波那契变种)(记忆化递归)
文章目录 上楼梯问题:递归解法探究问题定义解决方案1. 递归2. 记忆化递归关于python memo{}默认参数和字典的语法语法功能版本信息注意事项 结论 上楼梯问题:递归解法探究 在这篇文章中,将对上楼梯问题进行深入探讨。上楼梯问题是一种常见的…...

AI重新定义音视频生产力“新范式”
// 编者按:AIGC无疑是当下的热门话题和场景。面对AI带来的技术变革和算力挑战,该如何应对?LiveVideoStackCon 2023上海站邀请到了网心科技副总裁武磊为我们分享网心在面对AI应用场景和业务需求下的实践经验。 文/武磊 编辑/LiveVideoStack …...

Jmeter生成可视化的HTML测试报告
Jmeter也是可以生成测试报告的。 性能测试工具Jmeter由于其体积小、使用方便、学习成本低等原因,在现在的性能测试过程中,使用率越来越高,但其本身也有一定的缺点,比如提供的测试结果可视化做的很一般。 不过从3.0版本开始&…...

5G技术与其对智能城市、物联网和虚拟现实领域的影响
随着第五代移动通信技术(5G)的到来,我们即将迈向一个全新的数字化世界。5G技术的引入将带来更高的速度、更低的延迟和更大的连接性,推动了智能城市、物联网和虚拟现实等领域的发展。 首先,5G技术将带来超越以往的网络速…...

leetcode做题笔记88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终,合并后数组…...
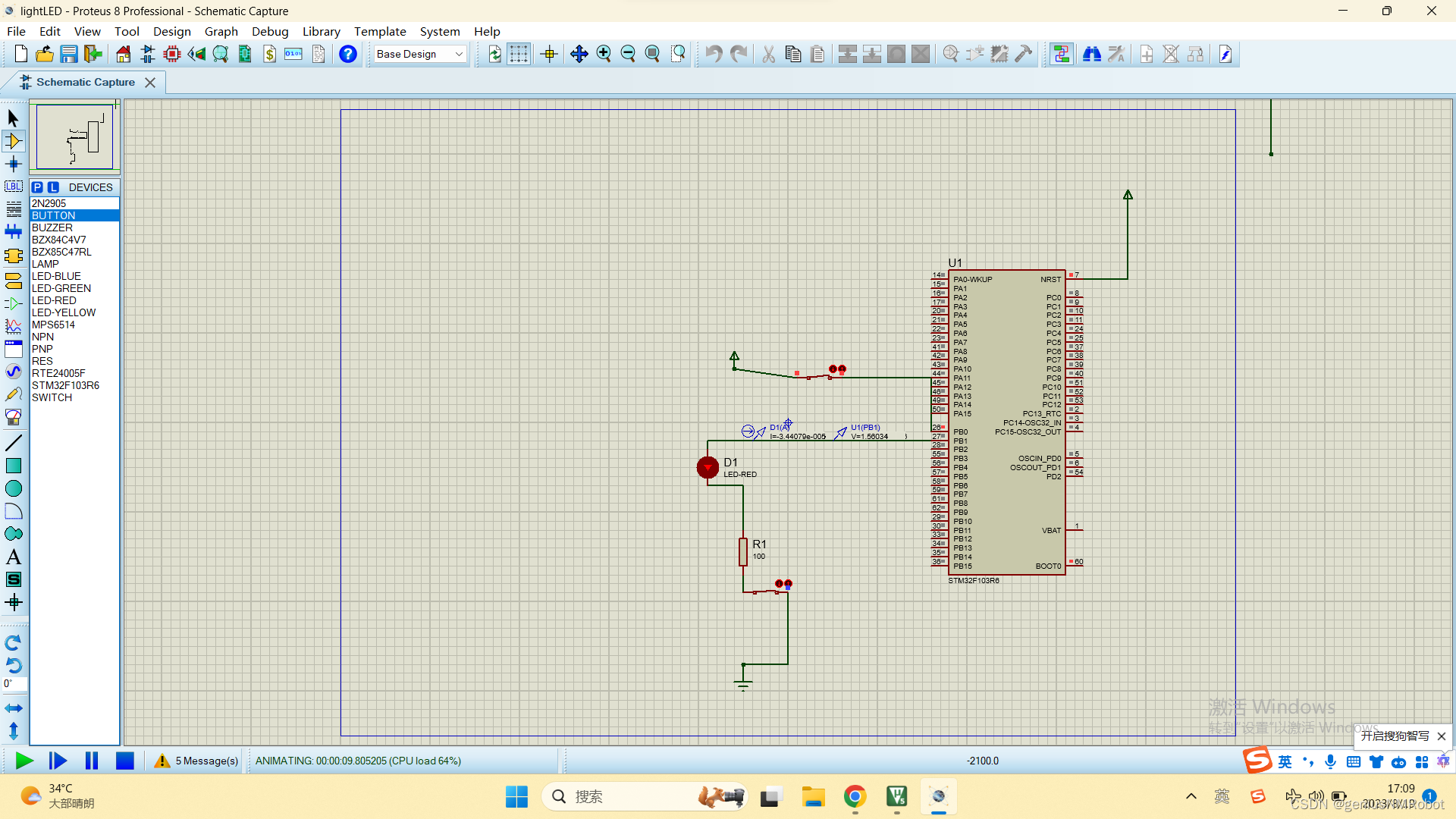
stm32开关控制led灯泡(附Proteus电路图)
说明:我的灯泡工作电压2V,电流设置为10um,注意了不是10毫安时微安啊,要不然电流太小亮不起来的。 2:我用的开关不是按钮button而是switch, 3:PB0,PB1默认都是低电平,采用了PULLDOWN模式,如果设…...

win10 wsl ubuntu 更换版本为18.04 apt换国内源Python换国内源;默认root
控制面板里面应用模块找到Ubuntu,可以卸载或者移动到其他盘。 Microsoft 应用程序 - ubuntu https://apps.microsoft.com/store/search/ubuntu?hlzh-cn&glcn&rtc1 选择想要的版本安装。 cp /etc/apt/sources.list /etc/apt/sources.list.bak nano /etc/ap…...

C++ Primer 第1章 开始
C Primer 第1章 开始 1.1 编写一个简单的C程序1.1.1 编译、运行程序一、程序源文件命名约定二、从命令行运行编译器 练习 1.2 初识输入输出一、标准输入输出对象二、一个使用IO库的程序三、向流写入数据四、使用标准库中的名字五、从流读取数据六、完成程序 1.3 注释简介一、C中…...
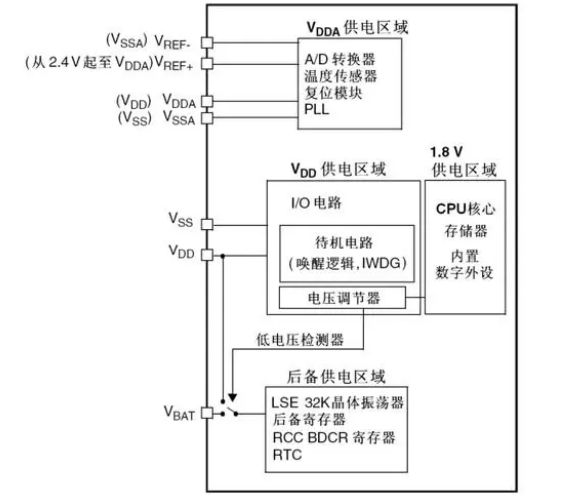
【STM32 学习】电源解析(VCC、VDD、VREF+、VBAT)
VCC电源电压GND电源供电负电压(通常接地)VDD模块工作正电压VSS模块工作负电压VREFADC参考正电压VREF-ADC参考负电压VBAT电池或其他电源供电VDDA模拟供电正电压VSSA模拟供电负电压 一、VCC(供电电压) VCC是指芯片的电源电压&#…...

C语言实例_解析GPS源数据
一、GPS数据格式介绍 GPS(全球定位系统)数据格式常见的是NMEA 0183格式,NMEA 0183格式是一种用于导航设备间传输数据的标准格式,定义了一套规范,使得不同厂商的设备可以通过串行通信接口(常见的是RS-232&a…...
LVS+Keepalived
Keepalived概述: keepalived软件 就是通过vrrp协议实现高可用功能 vrrp通信原理: vrrp就是虚拟路由冗余协议,它的出现就是为了解决静态路由的单点故障vrrp是通过一种竞选的一种协议机制将路由交给某台vrrp路由器vrrp用ip多播的方式【多播地…...

uni-app根据经纬度逆解析详细地址
uni-app中的getLocation()方法可以获取到用户当前的地理位置(经纬度)、速度。 但是返回参数中的address在app中才会显示,小程序中不会显示,所以我们需要进行逆解析其地址,解析出它的地址信息。 1.首先要在腾讯位置服务…...

【数据结构】吃透单链表!!!(详细解析~)
目录 前言:一.顺序表的缺陷 && 介绍链表1.顺序表的缺陷2.介绍链表(1)链表的概念(2)链表的结构(3)链表的功能 二.单链表的实现1.创建节点的结构2.头文件函数的声明3.函数的实现ÿ…...
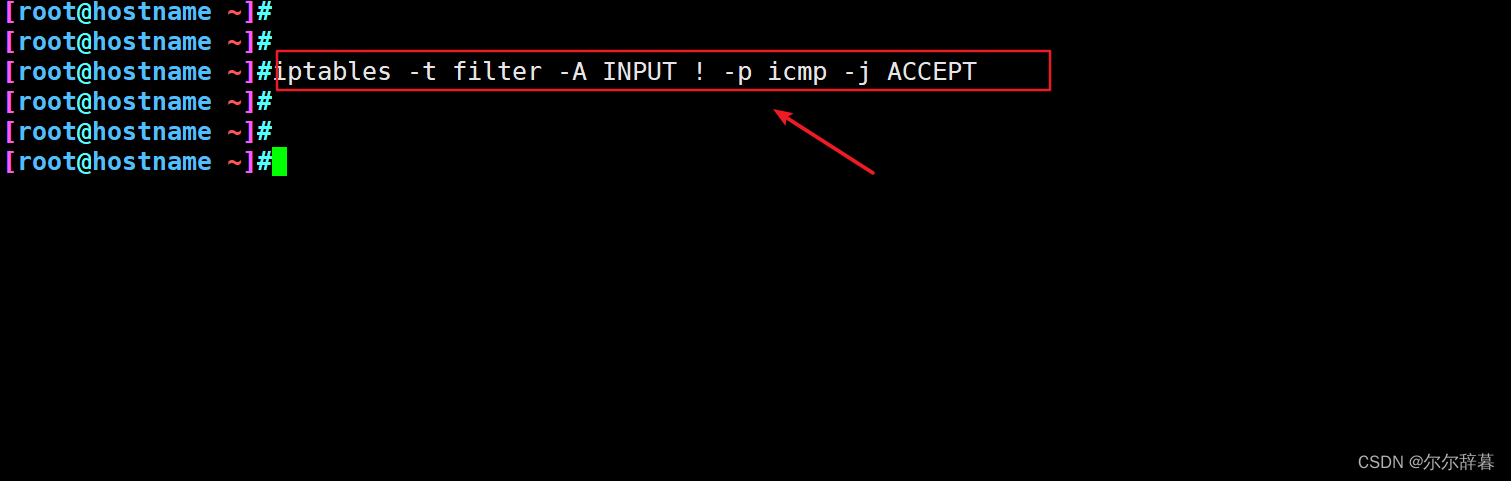
Linux 安全技术和防火墙
目录 1 安全技术 2 防火墙 2.1 防火墙的分类 2.1.1 包过滤防火墙 2.1.2 应用层防火墙 3 Linux 防火墙的基本认识 3.1 iptables & netfilter 3.2 四表五链 4 iptables 4.2 数据包的常见控制类型 4.3 实际操作 4.3.1 加新的防火墙规则 4.3.2 查看规则表 4.3.…...

Mac 开发 Tang Nano FPGA 指南(使用终端和使用 VS Code 和插件,适用所有 Gowin FPGA)
最近收到了一个 Tang nano 9K FPGA开发板,就想借此机会研究一下。 官方文档里介绍如果想使用高云的 FPGA,就需要使用 GOWIN IDE,但是需要申请 license 提交一堆资料,我是别人送的就不太方便让别人弄。加上 IDE 其实并不是很适合学…...

基于深度学习的铁路异物侵限检测算法研究_整体认知感觉欠点意思,但是有一个新的变形卷积-Octave 卷积
相比于其他的交通运输方式,铁路运输具有准时性高、连续性强、速度快、运输量大、运输成本低以及安全可靠等优点。同时由于国家高速铁路网络建设的不断推进,铁路运输逐渐成为我国客运与货运的主要运输方式。虽然铁路运输为人们出行和货物运输带来的极大的…...
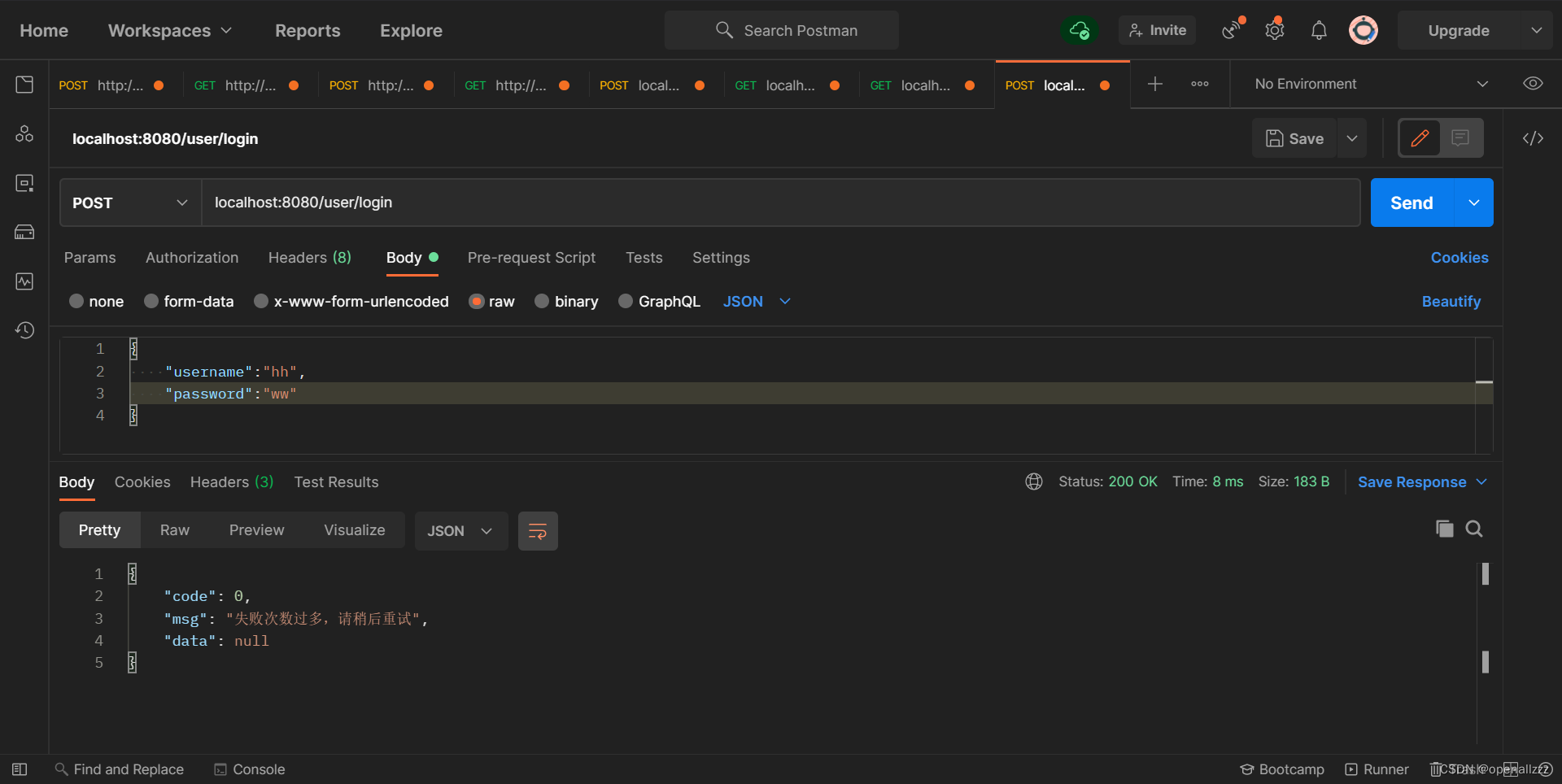
Spring项目使用Redis限制用户登录失败的次数以及暂时锁定用户登录权限
文章目录 背景环境代码实现0. 项目结构图(供参考)1. 数据库中的表(供参考)2. 依赖(pom.xml)3. 配置文件(application.yml)4. 配置文件(application-dev.yml)5…...

2023.8 - java - 变量类型
在Java语言中,所有的变量在使用前必须声明。声明变量的基本格式如下: type identifier [ value][, identifier [ value] ...] ; 格式说明: type -- 数据类型。identifier -- 是变量名,可以使用逗号 , 隔开来声明多个同类型变量…...

【Kubernetes】Kubernetes的Pod控制器
Pod控制器 一、Pod 控制器的概念1. Pod 控制器及其功用2. Pod 控制器有多种类型2.1 ReplicaSet2.2 Deployment2.3 DaemonSet2.4 StatefulSet2.5 Job2.6 Cronjob 3. Pod 与控制器之间的关系 二、Pod 控制器的使用1. Deployment2. SatefulSet2.1 为什么要有headless?2…...
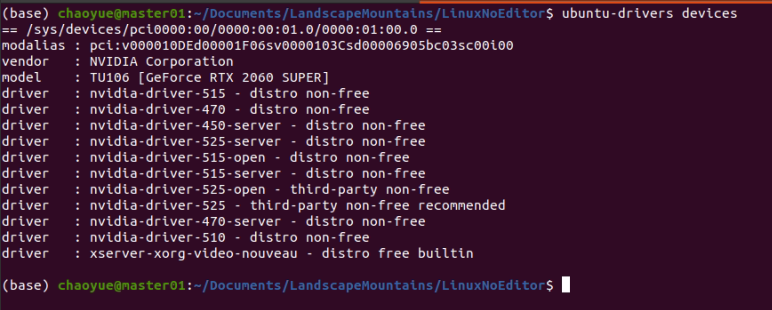
Ubuntu20.04安装Nvidia显卡驱动教程
1、禁用nouveau 1、创建文件,如果没有下载vim编辑器,将vim换成gedit即可 $ sudo vim /etc/modprobe.d/blacklist-nouveau.conf 2、在文件中插入以下内容,将nouveau加入黑名单,默认不开启 blacklist nouveau options nouveau m…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
