当前位置： 首页 > news >正文

Open3D 最小二乘拟合空间直线（方法一）

news 2026/2/9 23:47:44

目录

  • 一、算法原理
    • 1、空间直线
    • 2、最小二乘法拟合
  • 二、代码实现
  • 三、结果展示

在这里插入图片描述

本文由CSDN点云侠原创，原文链接。如果你不是在点云侠的博客中看到该文章，那么此处便是不要脸的爬虫。

一、算法原理

1、空间直线

x −

相关文章：

Open3D 最小二乘拟合空间直线（方法一）

目录 一、算法原理1、空间直线2、最小二乘法拟合二、代码实现三、结果展示本文由CSDN点云侠原创，原文链接。如果你不是在点云侠的博客中看到该文章，那么此处便是不要脸的爬虫。 一、算法原理 1、空间直线 x −...

编程日记 2023/8/20 10:06:36

解决uniapp 二次登陆 登录页是首页时，登录页闪现问题

pages.json文件中，pages数组中第一项是登录页，用户第一次登录后，存储登录状态，以后再进入应用时，自动登录跳转至首页。 但是自动登录跳转至首页时，登录页总是会闪现一下。 第一步：manifest.js…...

编程日记 2023/8/20 10:05:34

如何快速制作一个房地产电子传单？

在如今高度数字化的时代，电子传单成为了宣传推广的一种重要方式。下面将介绍如何利用乔拓云平台快速制作一个房地产电子传单。 第一步，找一个可靠的第三方制作平台/工具，比如乔拓云平台。乔拓云平台是一个功能强大、简单易用的电子传单制作工…...

编程日记 2023/8/20 10:04:32

golang云原生项目之：etcd服务注册与发现

服务注册与发现：ETCD 1直接调包 kitex-contrib： 上面有实现的案例，直接cv。下面是具体的理解 2 相关概念 EtcdResolver: etcd resolver是一种DNS解析器，用于将域名转换为etcd集群中的具体地址，以便应用程序可以与et…...

编程日记 2023/8/20 10:03:31

arm：day4

1. 实现三盏灯的点亮 .text .global _start_start: led1初始化函数LED_INIT: 1 通过RCC_AHB4_ENSETR寄存器&#xff0c;设置GPIOE F组控制器使能 0x50000A28[5:4]1ldr r0,0X50000A28ldr r1,[r0]orr r1,r1,#(0X3<<4)str r1,[r0] 2.1 通过GPIOE_MODER寄存器&#xff0c;…...

编程日记 2023/8/20 10:02:30

flutter 常见的状态管理器

flutter 常见的状态管理器 前言一、Provider二、Bloc三、Redux四、GetX总结 前言 当我们构建复杂的移动应用时&#xff0c;有效的状态管理是至关重要的&#xff0c;因为应用的不同部分可能需要共享数据、相应用户交互并保持一致的状态。Flutter 中有多种状态管理解决方案&#…...

编程日记 2023/8/20 10:01:27

Kotlin的Map

在 Kotlin 中&#xff0c;Map 是一种键值对的集合数据结构&#xff0c;用于存储一组关联的键和值。Kotlin 标准库提供了 Map 接口和多种实现类&#xff0c;使得操作和处理键值对数据更加方便。下面详细描述 Kotlin 的 Map 的用法&#xff1a; 创建 Map Kotlin 提供了几种方式…...

编程日记 2023/8/20 10:00:27

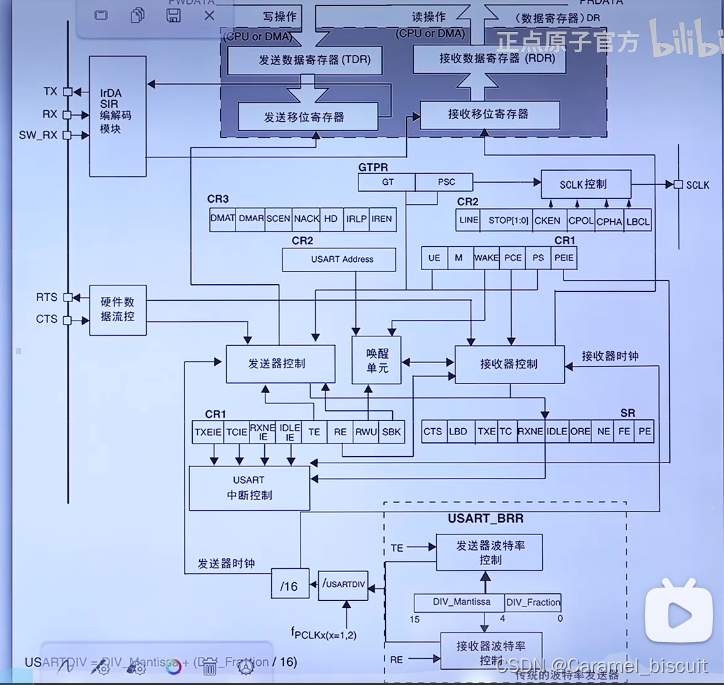
STM32 串口复习

按数据通信方式分类&#xff1a; 串行通信&#xff1a;数据逐位按顺序依次传输。传输速率较低&#xff0c;抗干扰能力较强&#xff0c;通信距离较长&#xff0c;I/O资源占用较少&#xff0c;成本较低。并行通信&#xff1a;数据各位通过多条线同时传输。 按数据传输方向分类&…...

编程日记 2023/8/20 9:59:23

VScode替换cmd powershell为git bash 终端，并设置为默认

效果图 步骤 1. 解决VScode缺少git bash的问题_failed to start bash - is git-bash.exe on the syst_Rudon滨海渔村的博客-CSDN博客效果解决步骤找到git安装目录下的/bin/bash.exe&#xff0c;复制其绝对路径&#xff0c;例如D:\Program Files\Git\bin\bash.exe把路径的右斜…...

编程日记 2023/8/20 9:58:22

网络基础(一)桥接网络

网络基础知识 桥接网络 桥接网络是一种网络设计技术&#xff0c;其目的是将两个或多个网络段连接在一起&#xff0c;使它们在逻辑上表现为单个网络。这通过使用网络桥来实现&#xff0c;网络桥工作在数据链路层&#xff08;第2层&#xff09;&#xff0c;只关心MAC地址&#…...

编程日记 2023/8/20 9:57:21

C#程序变量统一管理例子 - 开源研究系列文章

今天讲讲关于C#应用程序中使用到的变量的统一管理的代码例子。 我们知道&#xff0c;在C#里使用变量&#xff0c;除了private私有变量外&#xff0c;程序中使用到的公共变量就需要进行统一的存放和管理。这里笔者使用到的公共变量管理库划分为&#xff1a;1)窗体&#xff1b;2)…...

编程日记 2023/8/20 9:56:19

信息熵,信息增益,增益率的理解

西瓜数据集D如下: 编号色泽根蒂敲声纹理脐部触感好瓜1青绿蜷缩浊响清晰凹陷硬滑是2乌黑蜷缩沉闷清晰凹陷硬滑是3乌黑蜷缩浊响清晰凹陷硬滑是4青绿蜷缩沉闷清晰凹陷硬滑是5浅白蜷缩浊响清晰凹陷硬滑是6青绿稍蜷浊响清晰稍凹软粘是7乌黑稍蜷浊响稍糊稍凹软粘是8乌黑稍蜷浊响清晰…...

编程日记 2023/8/20 9:55:18

二级MySQL（一）——基本概念与方法

数据库系统的核心是【数据库管理系统】 E-R图提供了表示信息世界中的方法&#xff0c;主要有实体、属性和【联系】 E-R图是数据库设计的工具之一&#xff0c;一般适用于建立数据库的【概念模型】 将E-R图转换到关系模式时&#xff0c;实体与联系都可以表示成【关系】 关系数…...

编程日记 2023/8/20 9:54:16

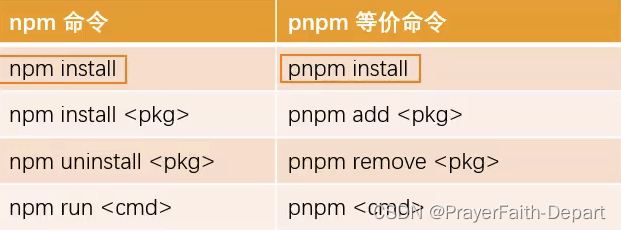
13 Web全栈 pnpm

什么是pnpm&#xff1f; 可以理解成performant npm缩写 速度快、节省磁盘空间的软件包管理器 特点 快速- pnpm比其他包管理器快2倍高效- node_modules中的文件链接自特定的内容寻址存储库支持monorepos- 内置支持单仓多包严格- pnpm默认创建了一个非平铺的node_modules 因此代…...

编程日记 2023/8/20 9:53:15

回归预测 | MATLAB实现CSO-BP布谷鸟优化算法优化BP神经网络多输入单输出回归预测（多指标，多图）

回归预测 | MATLAB实现CSO-BP布谷鸟优化算法优化BP神经网络多输入单输出回归预测&#xff08;多指标&#xff0c;多图&#xff09; 目录 回归预测 | MATLAB实现CSO-BP布谷鸟优化算法优化BP神经网络多输入单输出回归预测&#xff08;多指标&#xff0c;多图&#xff09;效果一览…...

编程日记 2023/8/20 9:52:14

JavaScript中的事件冒泡和事件捕获机制

聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 事件冒泡和事件捕获机制⭐ 事件冒泡&#xff08;Event Bubbling&#xff09;⭐ 事件捕获&#xff08;Event Capturing&#xff09;⭐ 停止事件传播⭐ 写在最后 ⭐ 专栏简介 前端入门之旅&#xff1a;探索Web开发的奇妙世界 记得点击上方或…...

编程日记 2023/8/20 9:51:13

秋招面经——结合各方面试经验

Mysql mysql事务 共享锁与排他锁 共享锁&#xff1a;允许一个事务去读一行&#xff0c;阻止其他事务获得相同数据集的排他锁。&#xff08;读都允许读&#xff0c;但我在读不允许你去改&#xff09; 排他锁&#xff1a;允许一个事务去读一行&#xff0c;阻止其他事务获得相同…...

编程日记 2023/8/20 9:50:11

Python random模块用法整理

随机数在计算机科学领域扮演着重要的角色&#xff0c;用于模拟真实世界的随机性、数据生成、密码学等多个领域。Python 中的 random 模块提供了丰富的随机数生成功能&#xff0c;本文整理了 random 模块的使用。 文章目录 Python random 模块注意事项Python random 模块的内置…...

编程日记 2023/8/20 9:49:10

【Redis从头学-5】Redis中的List数据类型实战场景之天猫热销榜单

&#x1f9d1;‍&#x1f4bb;作者名称&#xff1a;DaenCode &#x1f3a4;作者简介&#xff1a;啥技术都喜欢捣鼓捣鼓&#xff0c;喜欢分享技术、经验、生活。 &#x1f60e;人生感悟&#xff1a;尝尽人生百味&#xff0c;方知世间冷暖。 &#x1f4d6;所属专栏&#xff1a;Re…...

编程日记 2023/8/20 9:48:09

基于Python的HTTP代理爬虫开发初探

前言 随着互联网的发展&#xff0c;爬虫技术已经成为了信息采集、数据分析的重要手段。然而在进行爬虫开发的过程中&#xff0c;由于个人或机构的目的不同&#xff0c;也会面临一些访问限制或者防护措施。这时候&#xff0c;使用HTTP代理爬虫可以有效地解决这些问题&#xff0…...

编程日记 2023/8/20 9:47:08

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2026/2/7 23:18:31

【HTML-16】深入理解HTML中的块元素与行内元素

HTML元素根据其显示特性可以分为两大类&#xff1a;块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

编程新知 2025/11/11 6:28:42

【HarmonyOS 5 开发速记】如何获取用户信息（头像/昵称/手机号）

1.获取 authorizationCode&#xff1a; 2.利用 authorizationCode 获取 accessToken&#xff1a;文档中心 3.获取手机&#xff1a;文档中心 4.获取昵称头像&#xff1a;文档中心 首先创建 request 若要获取手机号&#xff0c;scope必填 phone&#xff0c;permissions 必填 …...

编程新知 2025/9/17 2:39:21

QT3D学习笔记——圆台、圆锥

类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体&#xff08;对象或容器&#xff09;QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质&#xff08;定义颜色、反光等&#xff09;QFirstPersonC…...

编程新知 2026/1/29 5:26:37

C#中的CLR属性、依赖属性与附加属性

CLR属性的主要特征 封装性&#xff1a; 隐藏字段的实现细节 提供对字段的受控访问 访问控制&#xff1a; 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性&#xff1a; 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑&#xff1a; 可以…...

编程新知 2025/12/4 0:13:33

搭建DNS域名解析服务器(正向解析资源文件)

正向解析资源文件 1&#xff09;准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2&#xff09;服务端安装软件&#xff1a;bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

编程新知 2026/2/4 15:42:45

tomcat指定使用的jdk版本

说明 有时候需要对tomcat配置指定的jdk版本号&#xff0c;此时&#xff0c;我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

编程新知 2025/6/10 21:11:28

MySQL的pymysql操作

本章是MySQL的最后一章&#xff0c;MySQL到此完结&#xff0c;下一站Hadoop&#xff01;&#xff01;&#xff01; 这章很简单&#xff0c;完整代码在最后&#xff0c;详细讲解之前python课程里面也有&#xff0c;感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

编程新知 2026/1/20 12:20:43

Python常用模块：time、os、shutil与flask初探

一、Flask初探 & PyCharm终端配置 目的： 快速搭建小型Web服务器以提供数据。 工具： 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask： 建议： 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装，避免频繁切换。 PyCharm Terminal 配置建议： 打开 Py…...

编程新知 2026/2/7 9:52:39

文件上传漏洞防御全攻略

要全面防范文件上传漏洞&#xff0c;需构建多层防御体系&#xff0c;结合技术验证、存储隔离与权限控制&#xff1a; &#x1f512; 一、基础防护层 前端校验&#xff08;仅辅助&#xff09; 通过JavaScript限制文件后缀名&#xff08;白名单&#xff09;和大小&#xff0c;提…...

编程新知 2025/8/18 19:05:00