信息熵,信息增益,增益率的理解
西瓜数据集D如下:
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | 青绿 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 3 | 乌黑 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 5 | 浅白 | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 9 | 乌黑 | 稍蜷 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 10 | 青绿 | 硬挺 | 清脆 | 清晰 | 平坦 | 软粘 | 否 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | 硬滑 | 否 |
| 12 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 软粘 | 否 |
| 13 | 青绿 | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | 稍凹 | 软粘 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 17 | 青绿 | 蜷缩 | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
信息熵: 描述信息的混乱程度,越接近1越混乱(纯度越低),0则不混乱(纯度越高)
- 信息熵是描述集合D的混乱程度(纯度)的值
- 以西瓜数据集为例,前7列(包含编号列)均为属性列,不是划分类别的指标,此例上一个瓜是否为好瓜是判断类别的唯一标准,则按照好瓜(是),好瓜(否)分为2类,即二分类问题
- 故D的信息熵仅由最后一列(好瓜)进行计算
- 简单看来:
- 好瓜的比例:(记为P(好瓜));
- 坏瓜的比例:(记为P(坏瓜)),
- 进行一次对比,最混乱情况也就是各一半,纯度最高情况则全部是好瓜/坏瓜.
- 如出现多个类别,则每个类别占比相同时最混乱,只有一个类别数据时纯度最高
- 举例说明
- (例1) 情况1.2的纯度大于情况1.1
( 情况 1.1 ) : P 好瓜 = 1 2 , P 坏瓜 = 1 2 (情况1.1):P_{ 好瓜} = \frac12,P_{坏瓜} = \frac12 (情况1.1):P好瓜=21,P坏瓜=21
( 情况 1.2 ) : P 好瓜 = 1 10 , P 坏瓜 = 9 10 (情况1.2):P_{ 好瓜} = \frac1{10},P_{坏瓜} = \frac9{10} (情况1.2):P好瓜=101,P坏瓜=109 - (例2) 情况2.2的纯度大于情况2.1
( 情况 2.1 ) : P 好瓜 = 2 10 , P 坏瓜 = 8 10 (情况2.1):P_{ 好瓜} = \frac2{10},P_{坏瓜} = \frac8{10} (情况2.1):P好瓜=102,P坏瓜=108
( 情况 2.2 ) : P 好瓜 = 1 10 , P 坏瓜 = 9 10 (情况2.2):P_{ 好瓜} = \frac1{10},P_{坏瓜} = \frac9{10} (情况2.2):P好瓜=101,P坏瓜=109 - 这样看来,在二分类问题中,取每个情况取最大的pk,比较大小,越大的纯度越高即可
- 但是三分类问题就会有点问题
- (例3) 情况3.2的纯度大于情况3.1
( 情况 3.1 ) : P 1 = 6 10 , P 2 = 2 10 , P 3 = 2 10 (情况3.1):P_1 = \frac6{10},P_2 = \frac2{10},P_3 = \frac2{10} (情况3.1):P1=106,P2=102,P3=102
( 情况 3.2 ) : P 1 = 6 10 , P 2 = 3 10 , P 3 = 1 10 (情况3.2):P_1 = \frac6{10},P_2 = \frac3{10},P_3 = \frac1{10} (情况3.2):P1=106,P2=103,P3=101
- (例1) 情况1.2的纯度大于情况1.1
- 在例3的情况下,仅仅比较最大值6/10都是一样的,那么就需要比较第二大的值,3/10>2/10,故3.2的纯度大于情况3.1
- 由此可见,比较两个样本D信息熵的方法有了
- 但是不太方便,如果要用一个值来量化纯度(混乱程度),思路很清晰,同一个情况(一个集合D)中的分类占比越大,则对纯度程度的贡献就越大.即在(情况3.2)中 6/10的纯度意义 > 3/10 > 1/10
- 使用log函数可以实现8提到的要求.pk值越小,则log(pk)会更小.选用以2为底的对数函数,故当前样本集合D中第k类样本所占比例为pk(k=1,2,3,…,|y|),则D的信息熵为:
E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D) = -\sum\limits _{k=1}^{|y|}p_klog_2p_k Ent(D)=−k=1∑∣y∣pklog2pk
信息增益: 使用某个属性a对样本集D进行划分所能获得的纯度提升程度
- 计算信息增益的目的,是选出一个属性,可以最大的划分数据
- 则:
信息增益 = 混乱程度 − 使用 a 进行划分后的混乱程度 信息增益 = 混乱程度 - 使用a进行划分后的混乱程度 信息增益=混乱程度−使用a进行划分后的混乱程度 - 则:
使用 a 进行划分后的混乱程度 = 即每个子集的混乱程度乘以各自的权重之和 使用a进行划分后的混乱程度 = 即每个子集的混乱程度乘以各自的权重之和 使用a进行划分后的混乱程度=即每个子集的混乱程度乘以各自的权重之和 - 又混乱程度可以使用信息熵Ent(D)进行计算
- 则可以推导,计算公式为:
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a) = Ent(D) - \sum\limits _{v=1}^V \frac{|Dv|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
- 注:
∣ D ∣ 即表示集合 D 中的元素个数 |D| 即表示集合D中的元素个数 ∣D∣即表示集合D中的元素个数
以西瓜数据集举例说明
- D包含若干属性,若使用某个属性a(即样本中的某列,例如色泽)对D进行划分,将D划分为多个子集
- 以西瓜数据为例,如使用属性色泽进行划分,则一共有3个属性值,则将全部数据划分为3个子集,即:
D 按照色泽划分 = D 青绿 ∪ D 乌黑 ∪ D 浅白 D_{按照色泽划分} = D_{青绿} \cup D_{乌黑} \cup D_{浅白} D按照色泽划分=D青绿∪D乌黑∪D浅白 - 故a在D上的信息增益为:
G a i n ( D , 色泽 ) = E n t ( D ) − ( ∣ D 青绿 ∣ ∣ D ∣ E n t ( D 青绿 ) + ∣ D 青绿 ∣ ∣ D ∣ E n t ( D 乌黑 ) ∣ D 浅白 ∣ ∣ D ∣ E n t ( D 浅白 ) ) Gain(D,{色泽}) = Ent(D) - (\frac{|D_{青绿}|}{|D|}Ent(D_{青绿}) +\frac{|D_{青绿}|}{|D|}Ent(D_{乌黑}) \frac{|D_{浅白}|}{|D|}Ent(D_{浅白}) ) Gain(D,色泽)=Ent(D)−(∣D∣∣D青绿∣Ent(D青绿)+∣D∣∣D青绿∣Ent(D乌黑)∣D∣∣D浅白∣Ent(D浅白)) - 可以看出,属性(色泽)对样本集D进行划分所能获得的纯度提升程度即为:Gain(D,色泽). 如每次都选择提升程度最大的一个,则决策树的分支越少.
增益率:排除子集数量对信息增益的影响
- 上文中求信息增益中,我们是忽略掉编号这一列的,因为按照编号属性进行计算信息增益,会划分17个子集,每个子集的信息熵Ent均为0,则信息增益Gain就是D的信息熵Ent
G a i n ( D , 编号 ) = E n t ( D ) − ( 0 + 0 + . . . . + 0 ) = E n t ( D ) = 0.998 Gain(D,{编号}) = Ent(D) - (0 + 0 + .... +0) = Ent(D) = 0.998 Gain(D,编号)=Ent(D)−(0+0+....+0)=Ent(D)=0.998 - 显然,这个信息增益非常高,单却是没有意义的,按照编号建立决策树,将会建立一个一层17分支的决策树.
- 故,我们需要找到一个方法,解决信息增益对数数目校多的属性偏好这一个问题
- 如使用Gain直接除V的数量(V是D按照属性a分组的所有子集,即D的子集数量),好像可以处理掉数目较多属性偏好的这个问题
G a i n ( D , 编号 ) V = 0.998 17 = 0.058 \frac {Gain(D,{编号})}{V} = \frac{0.998}{17} = 0.058 VGain(D,编号)=170.998=0.058 - 但是更适合的方法是除以IV(a),称为属性a的’固有值’(Intrinsic Value,IV),也称’ 分离信息 ’ (Split information):算法如下:
I V ( D , a ) = S p l i t I n f o r m a t i o n ( D , a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(D,a) =SplitInformation(D,a) = -\sum\limits _{v=1}^{V}\frac {|D^v|}{|D|}log_2\frac{|D^v|}{|D|} IV(D,a)=SplitInformation(D,a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣ - 故增益率定义为
G a i n _ r a t i o ( D , a ) = G a i n ( D , a ) I V ( D , a ) Gain\_ratio(D,a) = \frac{Gain(D,a)}{IV(D,a)} Gain_ratio(D,a)=IV(D,a)Gain(D,a) - 但是会带来一个新的问题,这个增益率会对数目较少的属性,有更强的偏好.(正好与信息增益的偏好相反)
8.故C4.5决策树算法,不是直接取增益率最高的属性,而是使用了一个启发式: 从候选划分属性中选出信息增益大于平均水平的属性,再选增益率最高的.
如有错误,敬请指正!
代码部分请参考:决策树代码实例(全部代码,包含绘图,ID.3算法,西瓜书示例)
相关文章:

信息熵,信息增益,增益率的理解
西瓜数据集D如下: 编号色泽根蒂敲声纹理脐部触感好瓜1青绿蜷缩浊响清晰凹陷硬滑是2乌黑蜷缩沉闷清晰凹陷硬滑是3乌黑蜷缩浊响清晰凹陷硬滑是4青绿蜷缩沉闷清晰凹陷硬滑是5浅白蜷缩浊响清晰凹陷硬滑是6青绿稍蜷浊响清晰稍凹软粘是7乌黑稍蜷浊响稍糊稍凹软粘是8乌黑稍蜷浊响清晰…...
——基本概念与方法)
二级MySQL(一)——基本概念与方法
数据库系统的核心是【数据库管理系统】 E-R图提供了表示信息世界中的方法,主要有实体、属性和【联系】 E-R图是数据库设计的工具之一,一般适用于建立数据库的【概念模型】 将E-R图转换到关系模式时,实体与联系都可以表示成【关系】 关系数…...
13 Web全栈 pnpm
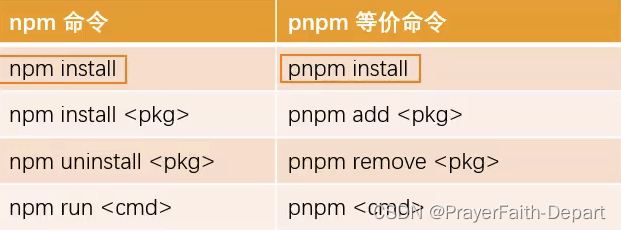
什么是pnpm? 可以理解成performant npm缩写 速度快、节省磁盘空间的软件包管理器 特点 快速- pnpm比其他包管理器快2倍高效- node_modules中的文件链接自特定的内容寻址存储库支持monorepos- 内置支持单仓多包严格- pnpm默认创建了一个非平铺的node_modules 因此代…...

回归预测 | MATLAB实现CSO-BP布谷鸟优化算法优化BP神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现CSO-BP布谷鸟优化算法优化BP神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现CSO-BP布谷鸟优化算法优化BP神经网络多输入单输出回归预测(多指标,多图)效果一览…...

JavaScript中的事件冒泡和事件捕获机制
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 事件冒泡和事件捕获机制⭐ 事件冒泡(Event Bubbling)⭐ 事件捕获(Event Capturing)⭐ 停止事件传播⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或…...

秋招面经——结合各方面试经验
Mysql mysql事务 共享锁与排他锁 共享锁:允许一个事务去读一行,阻止其他事务获得相同数据集的排他锁。(读都允许读,但我在读不允许你去改) 排他锁:允许一个事务去读一行,阻止其他事务获得相同…...

Python random模块用法整理
随机数在计算机科学领域扮演着重要的角色,用于模拟真实世界的随机性、数据生成、密码学等多个领域。Python 中的 random 模块提供了丰富的随机数生成功能,本文整理了 random 模块的使用。 文章目录 Python random 模块注意事项Python random 模块的内置…...

【Redis从头学-5】Redis中的List数据类型实战场景之天猫热销榜单
🧑💻作者名称:DaenCode 🎤作者简介:啥技术都喜欢捣鼓捣鼓,喜欢分享技术、经验、生活。 😎人生感悟:尝尽人生百味,方知世间冷暖。 📖所属专栏:Re…...

基于Python的HTTP代理爬虫开发初探
前言 随着互联网的发展,爬虫技术已经成为了信息采集、数据分析的重要手段。然而在进行爬虫开发的过程中,由于个人或机构的目的不同,也会面临一些访问限制或者防护措施。这时候,使用HTTP代理爬虫可以有效地解决这些问题࿰…...

时序预测 | MATLAB实现WOA-CNN-LSTM鲸鱼算法优化卷积长短期记忆神经网络时间序列预测
时序预测 | MATLAB实现WOA-CNN-LSTM鲸鱼算法优化卷积长短期记忆神经网络时间序列预测 目录 时序预测 | MATLAB实现WOA-CNN-LSTM鲸鱼算法优化卷积长短期记忆神经网络时间序列预测预测效果基本介绍模型描述程序设计学习总结参考资料 预测效果 基本介绍 时序预测 | MATLAB实现WOA-…...

每日一题之二进制中1的个数
二进制中1的个数 问题描述: 输入一个整数 n ,输出该数 32 位二进制表示中 1 的个数。其中负数用补码表示。 科普一下有符号数的三种表示:原码、反码和补码,可能有时候遗忘了。 真值:带有符号位的机器数(一…...

8.17校招 内推 面经
绿泡泡: neituijunsir 交流裙,内推/实习/校招汇总表格 1、校招 | 腾讯2024校园招聘全面启动(内推) 校招 | 腾讯2024校园招聘全面启动(内推) 2、校招 | 大华股份2024届全球校园招聘正式启动(内推) 校招 | 大华股份2024届全球校园招聘正式启动(内推) …...
VScode搭建Opencv(C++开发环境)
VScode配置Opencv 一、 软件版本二 、下载软件2.1 MinGw下载2.2 Cmake下载2.3 Opencv下载 三、编译3.1 cmake-gui3.2 make3.3 install 四、 VScode配置4.1 launch.json4.2 c_cpp_properties.json4.3 tasks.json 五、测试 一、 软件版本 cmake :cmake-3.27.2-windows-x86_64 Mi…...
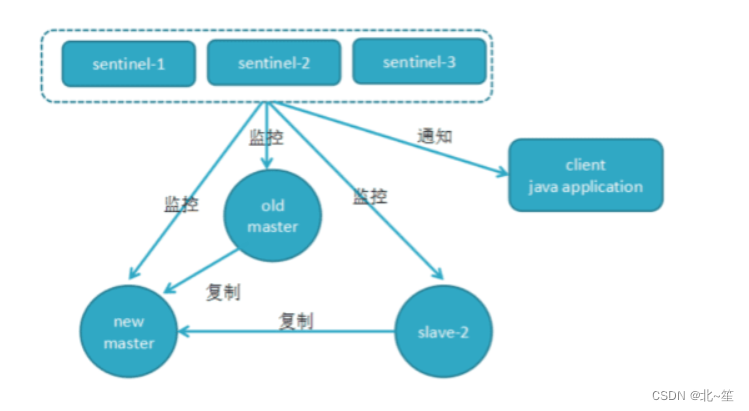
Redis高可用:哨兵机制(Redis Sentinel)详解
目录 1.什么是哨兵机制(Redis Sentinel) 2.哨兵机制基本流程 3.哨兵获取主从服务器信息 4.多个哨兵进行通信 5.主观下线和客观下线 6.哨兵集群的选举 7.新主库的选出 8.故障的转移 9.基于pub/sub机制的客户端事件通知 1.什么是哨兵机制…...
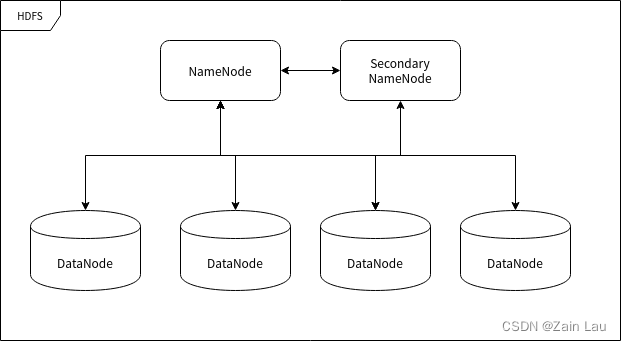
Hadoop小结(上)
最近在学大模型的分布式训练和存储,自己的分布式相关基础比较薄弱,基于深度学习的一切架构皆来源于传统,我总结了之前大数据的分布式解决方案即Hadoop: Why Hadoop Hadoop 的作用非常简单,就是在多计算机集群环境中营…...
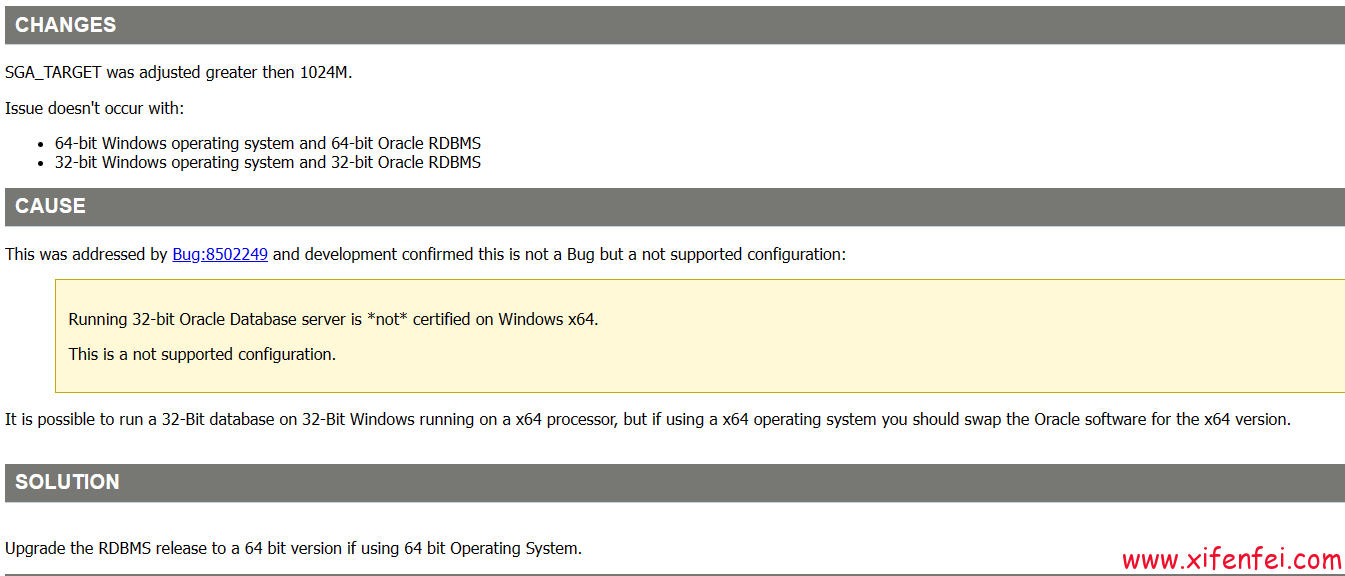
ORA-600 ksuloget2 恢复----惜分飞
客户在win 32位的操作系统上调至sga超过2G,数据库运行过程中报ORA-600 ksuloget2错误 Thread 1 cannot allocate new log, sequence 43586 Checkpoint not complete Current log# 1 seq# 43585 mem# 0: D:\ORACLE\ORADATA\ORCL\REDO01.LOG Fri Aug 04 14:57:02 2023 Errors i…...
NLP的tokenization
GPT3.5的tokenization流程如上图所示,以下是chatGPT对BPE算法的解释: BPE(Byte Pair Encoding)编码算法是一种基于统计的无监督分词方法,用于将文本分解为子词单元。它的原理如下: 1. 初始化:将…...

【宝藏系列】一文讲透C语言数组与指针的关系
【宝藏系列】嵌入式 C 语言代码优化技巧【超详细版】 文章目录 【宝藏系列】嵌入式 C 语言代码优化技巧【超详细版】👨🏫前言1️⃣指针1️⃣1️⃣指针的操作1️⃣2️⃣关于指针定义的争议1️⃣3️⃣对教材错误写法的小看法 2️⃣指针和数组的区别2️⃣…...

Jenkins+Jmeter集成自动化接口测试并通过邮件发送测试报告
一、Jenkins的配置 1、新增一个自由风格的项目 2、构建->选择Excute Windows batch command(因为我是在本地尝试的,因此选择的windows) 3、输入步骤: 1. 由于不能拥有相同的jtl文件,因此在每次构建前都需要删除jtl…...

clickhouse入门
clickhouse 1 课程介绍 和hadoop无关,俄罗斯,速度快3 介绍&特点 1 列式存储 在线分析处理。 使用sql进行查询。列式存储更适合查询分析的场景。新增时候有一个寻址的过程。更容易进行压缩行式存储。增删改查都需要的时候。2 DBMS功能 包括ddl,d…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
