Kubernetes(K8s)从入门到精通系列之十七：minikube启动K8s dashboard
相关文章：
从入门到精通系列之十七：minikube启动K8s dashboard)
Kubernetes(K8s)从入门到精通系列之十七：minikube启动K8s dashboard
Kubernetes K8s从入门到精通系列之十七：minikube启动K8s dashboard 一、安装minikube的详细步骤二、查看Pod三、启动dashboard四、创建代理访问dashboard五、远程访问dashboard一、安装minikube的详细步骤 Kubernetes(K8s)从入门到精通系列之十六：linux服务器安装minikube的详…...
C++ 网络编程项目fastDFS分布式文件系统（五)--nginx+fastdfs
目录 1. 文件上传下载流程 2. Nginx和fastDFS的整合 3. 数据库表 3.1 数据库操 3.2 数据库建表 1. 文件上传下载流程 fileID 需要是一个哈希来判定。 2. 文件下载流程 3. 优化 优化思路 : 直接让客户端连接 fastDFS 的存储节点 , 实现文件下载 举例 , 访问一个…...
)
开发者本地搭建性能监测工具(Windows)
ElasticSearch 8.9.0 开发模式安装 JDK安装 官方提供版本与JDK支持关系：https://www.elastic.co/cn/support/matrix#matrix_jvm 我们安装Elasticsearch 8.9.x，看到支持的最低JDK版本是17。 JDK（Windows/Mac含M1/M2 Arm原生JDK）…...
嵌入式Linux开发实操（八）：UART串口开发
串口可以说是非常好用的一个接口，它同USB、CAN、I2C、SPI等接口一样，为SOC/MCU构建了丰富的接口功能。那么在嵌入式linux中又是如何搭建和使用UART接口的呢？ 一、Console接口即ttyS0 ttyS0通常做为u-boot(bootloader的一种，像是Windows的BIOS)，它需要一个交互界面，一般…...
公告：微信小程序备案期限官方要求
备案期限要求 1、若微信小程序未上架，自2023年9月1日起，微信小程序须完成备案后才可上架，备案时间1-20日不等； 2、若微信小程序已上架，请于2024年3月31日前完成备案，逾期未完成备案，平台将按照…...
cesium中获取高度的误区
this.ellipsoid viewer.scene.globe.ellipsoid; var cartesian viewer.camera.pickEllipsoid(e.position, this.ellipsoid);if(cartesian){// 苗卡尔椭球体的三维坐标 转 地图坐标（弧度）var cartographic viewer.scene.globe.ellipsoid.cartesianToCa…...
基于Centos：服务器基础环境安装： JDK、Maven、Python、Go、Docker、K8s
创建用户 useradd dev groupadd op chown -R :op /opt chmod -R 770 /opt usermod -aG op devJDK8 yum install -y java-1.8.0-openjdk-devel echo export JAVA_HOME/usr/lib/jvm/java-1.8.0/>> /etc/profilesource /etc/profileJDK11 yum install -y java-11-openjd…...
Elasticsearch的数据删除策略只能触发一次
在Elasticsearch中，可以使用Index Lifecycle Management（ILM）来设置删除数据的保留时长。ILM是Elasticsearch的一项功能，用于管理索引的生命周期，包括数据保留、备份、归档等操作。 要设置删除数据的保留时长…...
Open3D 最小二乘拟合空间直线（方法一）
目录 一、算法原理1、空间直线2、最小二乘法拟合二、代码实现三、结果展示本文由CSDN点云侠原创，原文链接。如果你不是在点云侠的博客中看到该文章，那么此处便是不要脸的爬虫。 一、算法原理 1、空间直线 x −...
解决uniapp 二次登陆 登录页是首页时，登录页闪现问题
pages.json文件中，pages数组中第一项是登录页，用户第一次登录后，存储登录状态，以后再进入应用时，自动登录跳转至首页。 但是自动登录跳转至首页时，登录页总是会闪现一下。 第一步：manifest.js…...
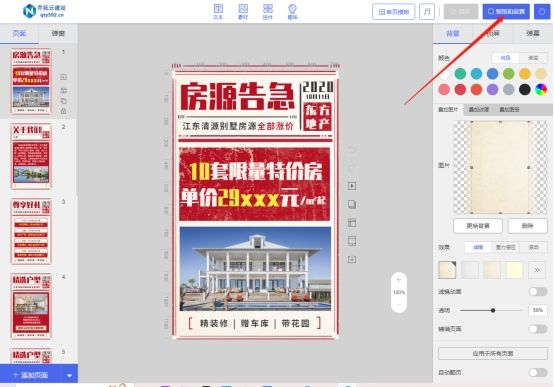
如何快速制作一个房地产电子传单？
在如今高度数字化的时代，电子传单成为了宣传推广的一种重要方式。下面将介绍如何利用乔拓云平台快速制作一个房地产电子传单。 第一步，找一个可靠的第三方制作平台/工具，比如乔拓云平台。乔拓云平台是一个功能强大、简单易用的电子传单制作工…...
golang云原生项目之：etcd服务注册与发现
服务注册与发现：ETCD 1直接调包 kitex-contrib： 上面有实现的案例，直接cv。下面是具体的理解 2 相关概念 EtcdResolver: etcd resolver是一种DNS解析器，用于将域名转换为etcd集群中的具体地址，以便应用程序可以与et…...
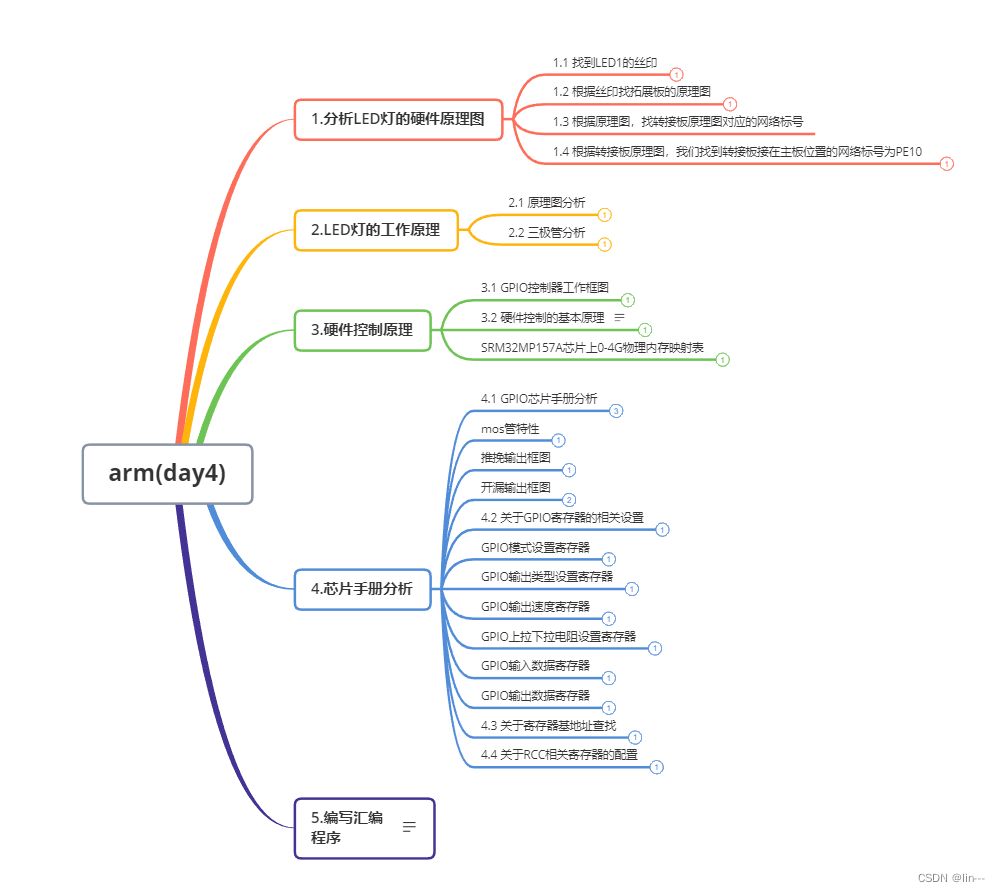
arm：day4
1. 实现三盏灯的点亮 .text .global _start_start: led1初始化函数LED_INIT: 1 通过RCC_AHB4_ENSETR寄存器，设置GPIOE F组控制器使能 0x50000A28[5:4]1ldr r0,0X50000A28ldr r1,[r0]orr r1,r1,#(0X3<<4)str r1,[r0] 2.1 通过GPIOE_MODER寄存器，…...
flutter 常见的状态管理器
flutter 常见的状态管理器 前言一、Provider二、Bloc三、Redux四、GetX总结 前言 当我们构建复杂的移动应用时，有效的状态管理是至关重要的，因为应用的不同部分可能需要共享数据、相应用户交互并保持一致的状态。Flutter 中有多种状态管理解决方案&#…...
Kotlin的Map
在 Kotlin 中，Map 是一种键值对的集合数据结构，用于存储一组关联的键和值。Kotlin 标准库提供了 Map 接口和多种实现类，使得操作和处理键值对数据更加方便。下面详细描述 Kotlin 的 Map 的用法： 创建 Map Kotlin 提供了几种方式…...
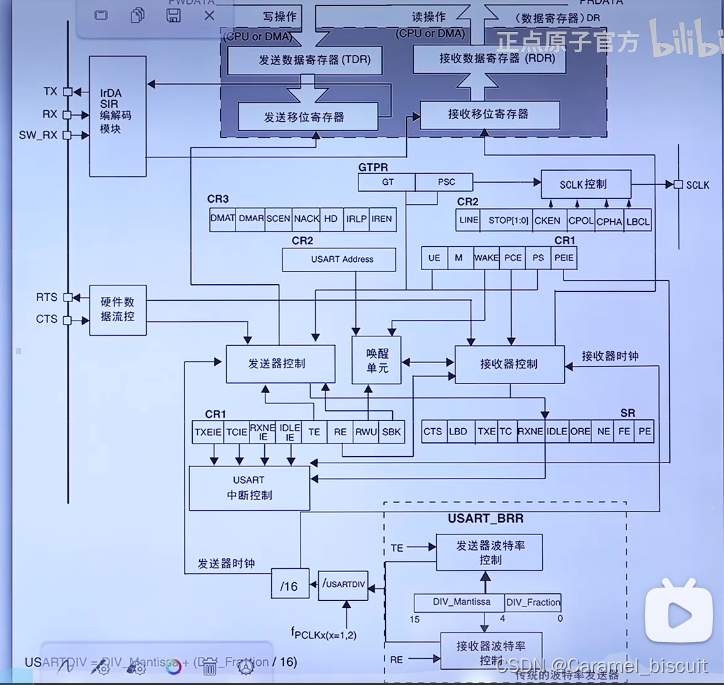
STM32 串口复习
按数据通信方式分类： 串行通信：数据逐位按顺序依次传输。传输速率较低，抗干扰能力较强，通信距离较长，I/O资源占用较少，成本较低。并行通信：数据各位通过多条线同时传输。 按数据传输方向分类&…...
VScode替换cmd powershell为git bash 终端，并设置为默认
效果图 步骤 1. 解决VScode缺少git bash的问题_failed to start bash - is git-bash.exe on the syst_Rudon滨海渔村的博客-CSDN博客效果解决步骤找到git安装目录下的/bin/bash.exe，复制其绝对路径，例如D:\Program Files\Git\bin\bash.exe把路径的右斜…...
桥接网络)
网络基础(一)桥接网络
网络基础知识 桥接网络 桥接网络是一种网络设计技术，其目的是将两个或多个网络段连接在一起，使它们在逻辑上表现为单个网络。这通过使用网络桥来实现，网络桥工作在数据链路层（第2层），只关心MAC地址&#…...
C#程序变量统一管理例子 - 开源研究系列文章
今天讲讲关于C#应用程序中使用到的变量的统一管理的代码例子。 我们知道，在C#里使用变量，除了private私有变量外，程序中使用到的公共变量就需要进行统一的存放和管理。这里笔者使用到的公共变量管理库划分为：1)窗体；2)…...
信息熵,信息增益,增益率的理解
西瓜数据集D如下: 编号色泽根蒂敲声纹理脐部触感好瓜1青绿蜷缩浊响清晰凹陷硬滑是2乌黑蜷缩沉闷清晰凹陷硬滑是3乌黑蜷缩浊响清晰凹陷硬滑是4青绿蜷缩沉闷清晰凹陷硬滑是5浅白蜷缩浊响清晰凹陷硬滑是6青绿稍蜷浊响清晰稍凹软粘是7乌黑稍蜷浊响稍糊稍凹软粘是8乌黑稍蜷浊响清晰…...
【kafka】Golang实现分布式Masscan任务调度系统
要求： 输出两个程序，一个命令行程序（命令行参数用flag）和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽，然后将消息推送到kafka里面。 服务端程序： 从kafka消费者接收…...
【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验
系列回顾： 在上一篇中，我们成功地为应用集成了数据库，并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了！但是，如果你仔细审视那些 API，会发现它们还很“粗糙”：有…...
数据库分批入库
今天在工作中，遇到一个问题，就是分批查询的时候，由于批次过大导致出现了一些问题，一下是问题描述和解决方案： 示例： // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
根据万维钢·精英日课6的内容，使用AI（2025）可以参考以下方法：
根据万维钢精英日课6的内容，使用AI（2025）可以参考以下方法： 四个洞见 模型已经比人聪明：以ChatGPT o3为代表的AI非常强大，能运用高级理论解释道理、引用最新学术论文，生成对顶尖科学家都有用的…...
Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...
华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步：前置条件，启用 OLE 自动化方式 1：使用 SQL 实现启用 OLE 自动化方式 2：Sql Server 2005启动OLE自动化方式 3：Sql Server 2008启动OLE自动化第 2 步：创建存储过程第 3 步：创建触发器扩展 - 如何调试？第 1 步：登录 SQL Server 2008第 2 步…...
ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
WebRTC调研
WebRTC是什么，为什么，如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
机器学习的数学基础：线性模型
线性模型 线性模型的基本形式为： f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法，得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...