第 359 场 LeetCode 周赛题解
A 判别首字母缩略词
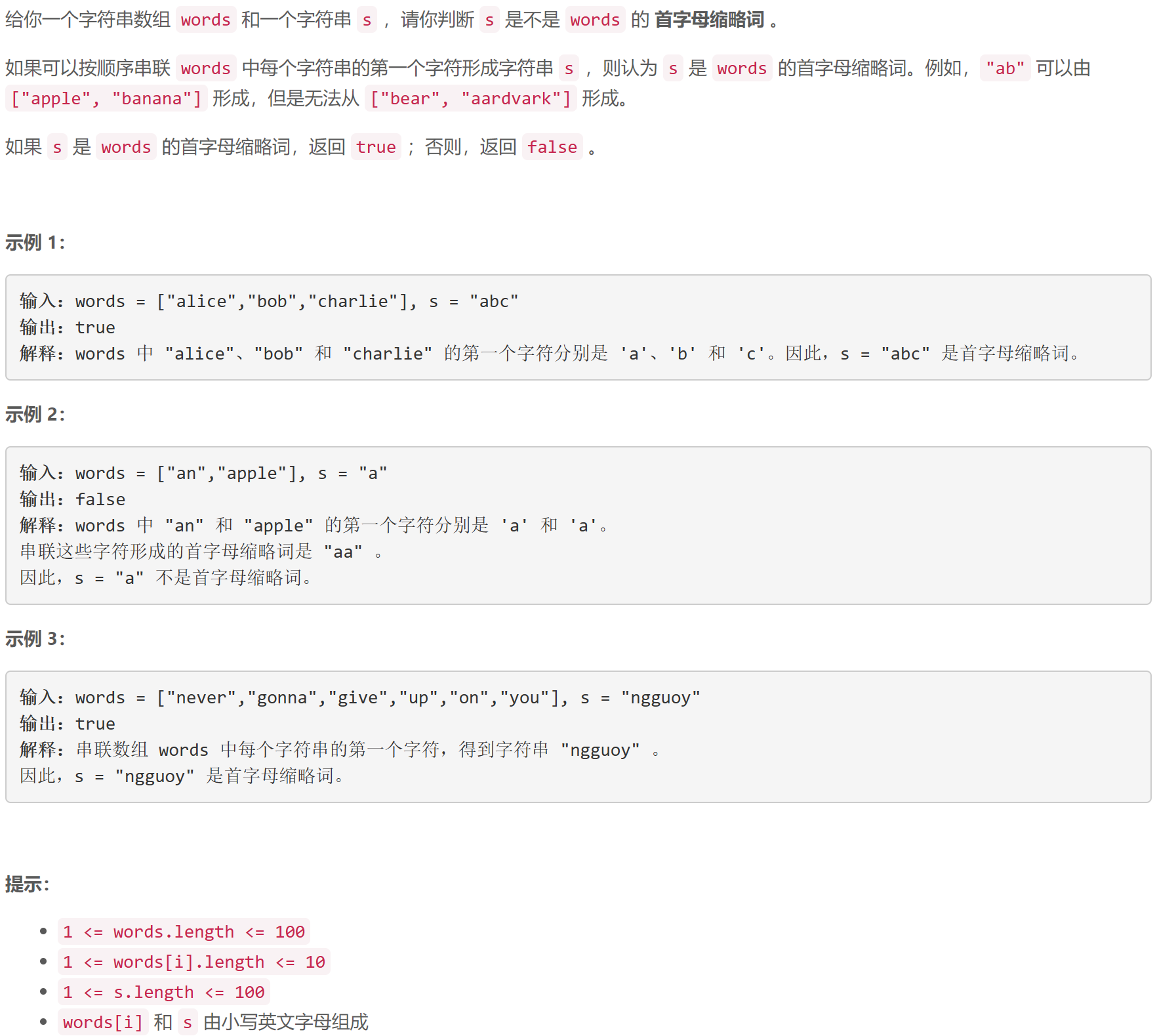
签到题…
class Solution {
public:bool isAcronym(vector<string> &words, string s) {string pf;for (auto &s: words)pf.push_back(s[0]);return pf == s;}
};
B k-avoiding 数组的最小总和
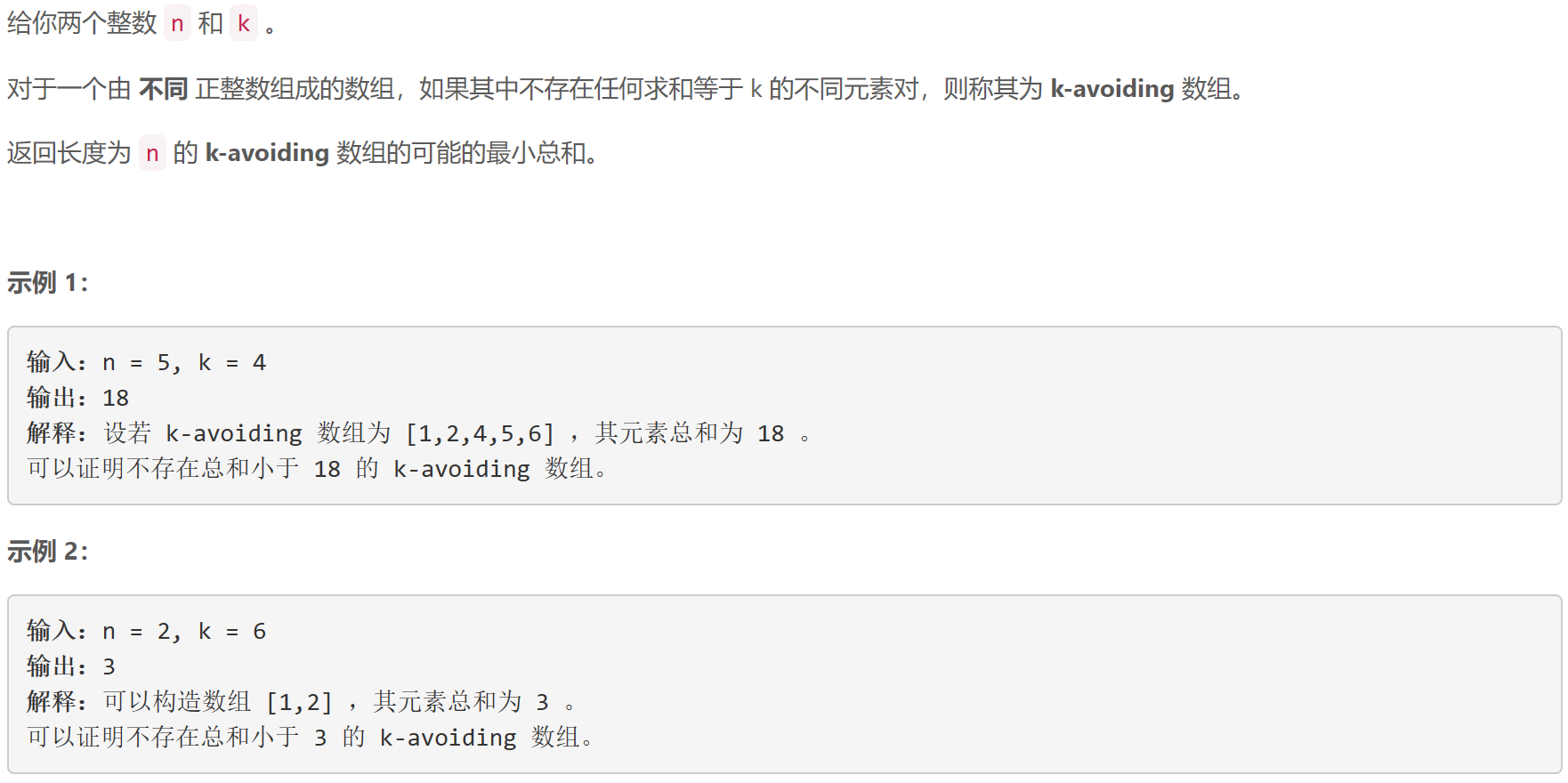
贪心:从 1 1 1开始升序枚举,判断当前数是否可以放入数组,同时维护当前数组中的数,直到找到 n n n个数。
class Solution {
public:int minimumSum(int n, int k) {set<int> vis;int s = 0;for (int i = 1; vis.size() < n; i++) {if (vis.count(k - i))continue;vis.insert(i);s += i;}return s;}
};
C 销售利润最大化
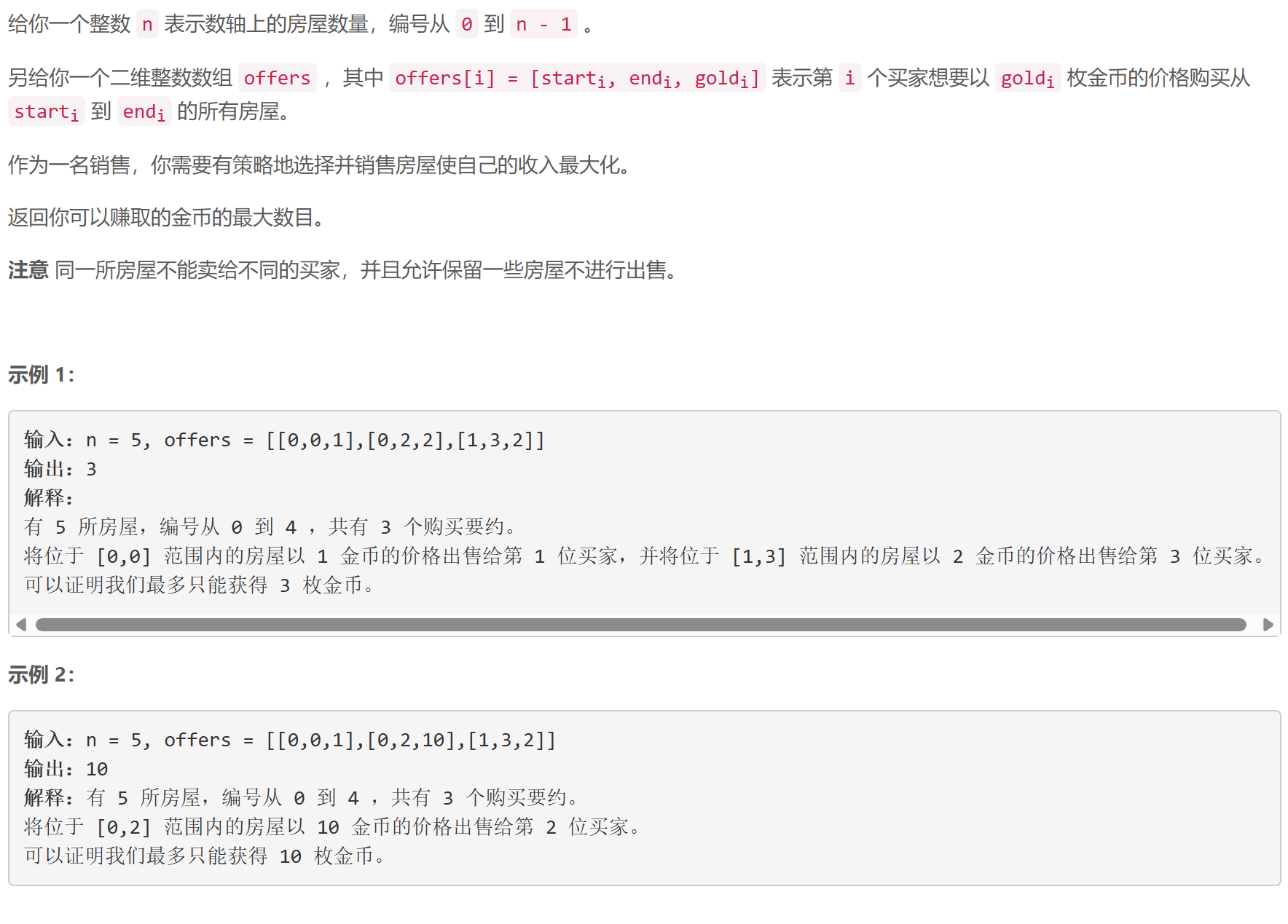

动态规划+树状数组:首先将 o f f e r s offers offers按 s t a r t i start_i starti升序排序,枚举 o f f e r s offers offers中的元素,设 p [ i ] p[i] p[i]为销售的最右区间的右端点为 i i i的情况下能够得到的最大利润,设当前元素为 [ l , r , g ] [l, r, g] [l,r,g],则可以更新状态: p [ r ] = m a x { p [ r ] m a x { p [ k ] ∣ 0 ≤ k ≤ l − 1 } + g p[r]=max\left\{\begin{matrix} p[r] \\ max\{p[k] \;|\; 0\le k \le l-1 \} + g \end{matrix}\right. p[r]=max{p[r]max{p[k]∣0≤k≤l−1}+g
利用树状数组来维护前缀上的极大值。
class Solution {
public:int maximizeTheProfit(int n, vector<vector<int>> &offers) {N = n + 5;a = vector<int>(N, 0);sort(offers.begin(), offers.end());int res = 0;for (auto &it: offers) {int l = it[0] + 1, r = it[1] + 1, g = it[2];//树状数组中下标从1开始int cur = query(l - 1) + g;//查询前缀极大值res = max(res, cur);update(r, cur); //树状数组更新}return res;}int N;vector<int> a;//树状数组inline int lowbit(int x) {return x & -x;}void update(int loc, int val) {// li[loc]=max(li[loc], val);for (; loc < N; loc += lowbit(loc))a[loc] = max(a[loc], val);}int query(int loc) {// max{li[k] | 1<=k<=loc}int res = 0;for (; loc > 0; loc -= lowbit(loc))res = max(res, a[loc]);return res;}
};
D 找出最长等值子数组
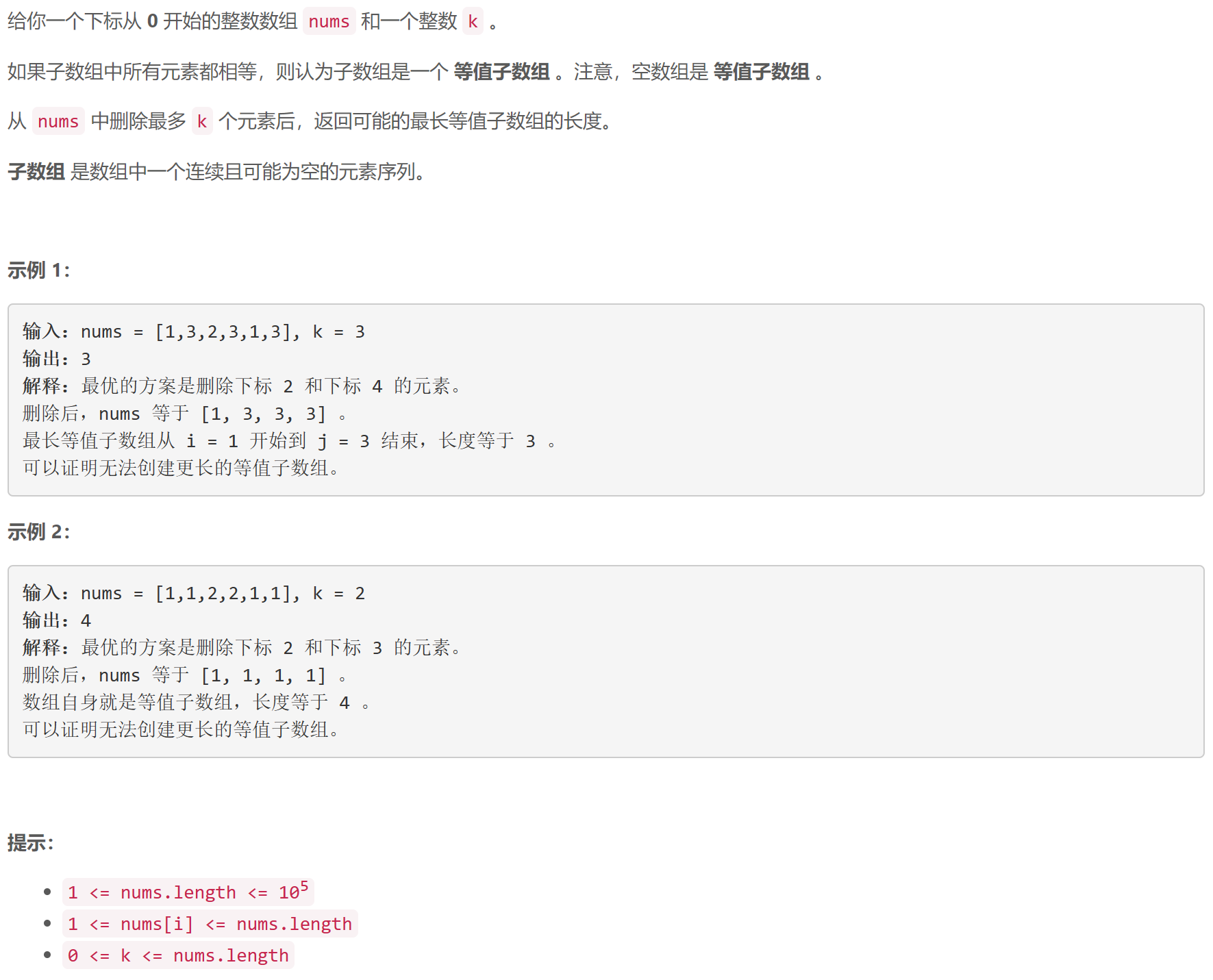
二分+哈希:用二分查找答案 l e n len len,这样问题就变成了:判断从 n u m s nums nums 中删除最多 k k k 个元素后,是否存在长为 l e n len len 的等值子数组。设 l o c [ v ] loc[v] loc[v]为 n u m s nums nums中所有 v v v所在下标组成的升序数组,若存在 0 ≤ i ≤ i + l e n − 1 < l o c [ v ] . s i z e ( ) 0\le i \le i+len-1 < loc[v].size() 0≤i≤i+len−1<loc[v].size() 使得 l o c [ v ] [ i + l e n − 1 ] − l o c [ v ] [ i ] + 1 − l e n ≤ k loc[v][i + len - 1] - loc[v][i] + 1 - len \le k loc[v][i+len−1]−loc[v][i]+1−len≤k,则说明可以得到长为 l e n len len 的值为 v v v的等值子数组,枚举 n u m s nums nums中不同的数,即可判断是否可以得到长为 l e n len len 的等值子数组。
class Solution {
public:int longestEqualSubarray(vector<int> &nums, int k) {int n = nums.size(), l = 1, r = n;unordered_map<int, vector<int>> loc;for (int i = 0; i < n; i++)loc[nums[i]].push_back(i);auto can = [&](int len) {//判断是否可以得到长为len的等值子数组int find = 0;for (auto &[_, vec]: loc) {//枚举不同的数for (int i = 0; i + len - 1 < vec.size(); i++)if (vec[i + len - 1] - vec[i] + 1 - len <= k)return true;}return false;};while (l < r) {//二分查找答案int mid = (l + r + 1) / 2;if (can(mid))l = mid;elser = mid - 1;}return l;}
};
相关文章:

第 359 场 LeetCode 周赛题解
A 判别首字母缩略词 签到题… class Solution { public:bool isAcronym(vector<string> &words, string s) {string pf;for (auto &s: words)pf.push_back(s[0]);return pf s;} };B k-avoiding 数组的最小总和 贪心:从 1 1 1开始升序枚举,…...

【开源项目】Stream-Query的入门使用和原理分析
前言 无意间发现了一个有趣的项目,Stream-Query。了解了一下其基本的功能,可以帮助开发者省去Mapper的编写。在开发中,我们会编写entity和mapper来完成业务代码,但是Stream-Query可以省去mapper,只写entity。 快速入…...

微信小程序picker组件的简单使用 单选
<picker mode"selector" range"{{classData}}" bindchange"bindClassChange" value"{{classIndex}}" range-key"className"><view class"picker">{{classData[classIndex].className || 请选择班级}}…...
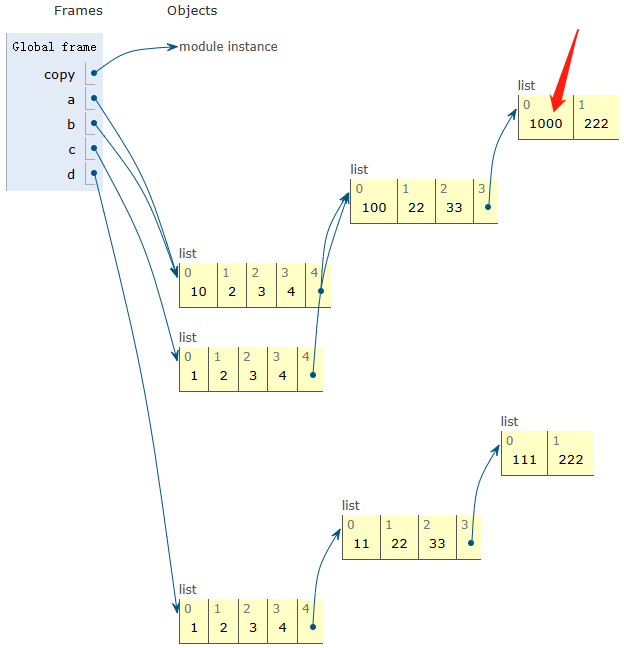
python、numpy、pytorch中的浅拷贝和深拷贝
1、Python中的浅拷贝和深拷贝 import copya [1, 2, 3, 4, [11, 22, 33, [111, 222]]] b a c a.copy() d copy.deepcopy(a)print(before modify\r\n a\r\n, a, \r\n,b a\r\n, b, \r\n,c a.copy()\r\n, c, \r\n,d copy.deepcopy(a)\r\n, d, \r\n)before modify a [1, 2…...

EasyRecovery14数据恢复软件支持各类存储设备的数据恢复
EasyRecovery14数据恢复软件专业数据恢复软件支持电脑、相机、移动硬盘、U盘、SD卡、内存卡、光盘、本地电子邮件和 RAID 磁盘阵列等各类存储设备的数据恢复。 目前市面上有许多数据恢复软件,但褒贬不一,而且数据恢复软件又不是一款会被经常使用的软件&a…...
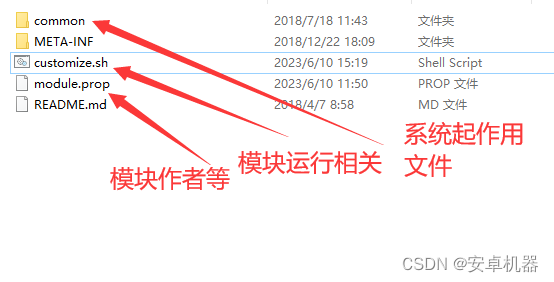
玩机搞机----面具模块的组成 制作模块
root面具相信很多玩家都不陌生。早期玩友大都使用第三方卡刷补丁来对系统进行各种修复和添加功能。目前面具补丁代替了这些操作。今天的帖子了解下面具各种模块的组成和几种普遍的代码组成。 Magisk中运行的每个单独的shell脚本都将在内部的BusyBox的shell中执行。对于与第三方…...
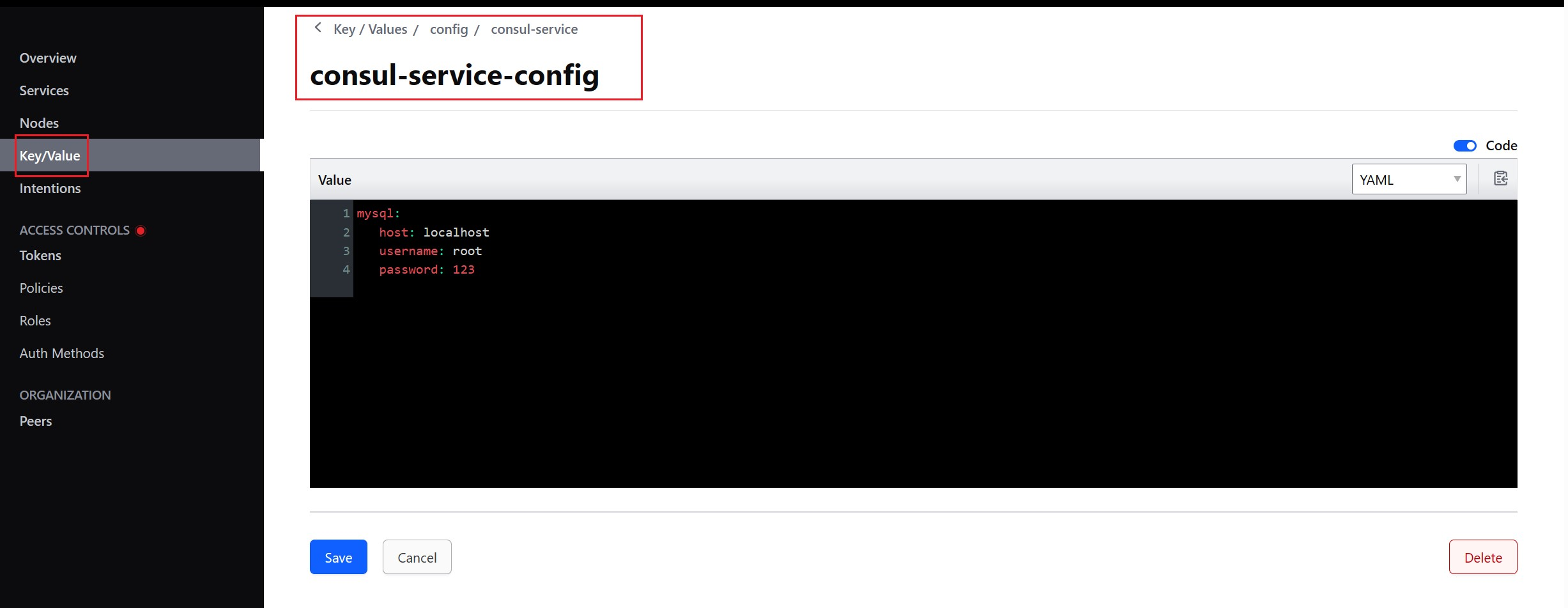
注册中心/配置管理 —— SpringCloud Consul
Consul 概述 Consul 是一个可以提供服务发现,健康检查,多数据中心,key/Value 存储的分布式服务框架,用于实现分布式系统的发现与配置。Cousul 使用 Go 语言实现,因此天然具有可移植性,安装包仅包含一个可执…...
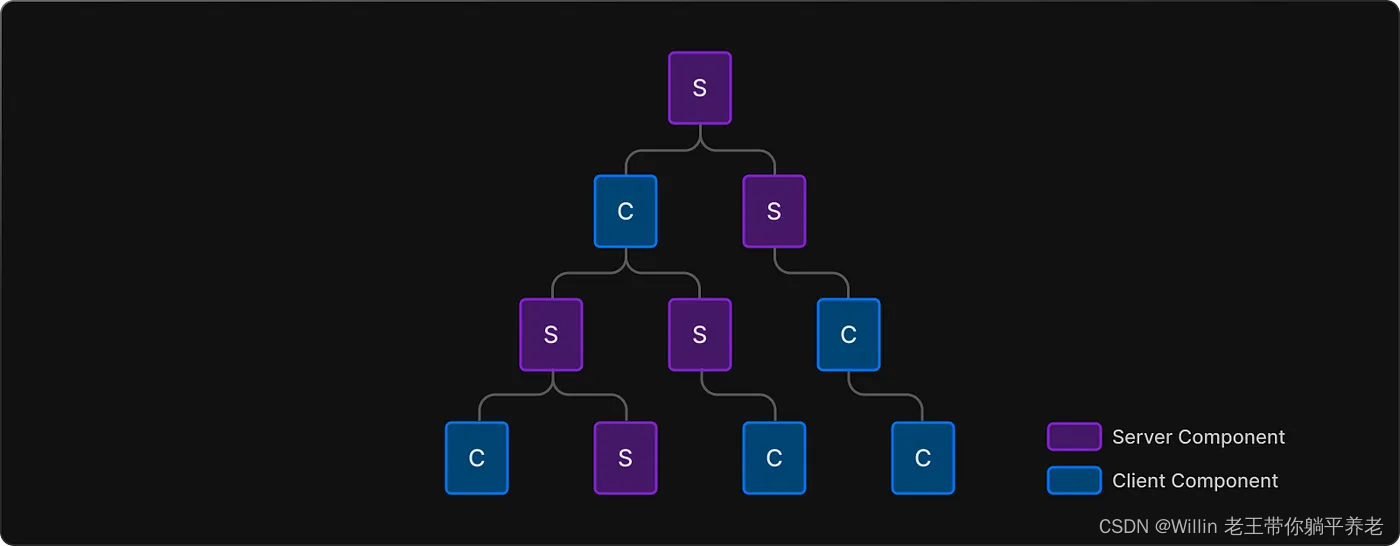
Next.js 13 你需要了解的 8 件事
目录 React 服务器组件 (RSC)服务器组件默认开启在 Next.js 中客户端组件也在服务器上呈现!组成客户端和服务器组件编译Next.js 13 渲染模式桶文件有点坏了库集成:WIP 仍在进行中Route groups 路由组总结 在本文中,我们…...
算法详解)
计数排序(Count Sort)算法详解
1. 算法简介 计数排序(Count Sort)是一种非比较排序算法,其核心思想是统计数组中每个元素出现的次数,然后根据统计结果将元素按照顺序放回原数组中。计数排序的时间复杂度为O(nk),其中n是数组的长度,k是数…...
Linux驱动开发(Day3)
驱动点灯:...
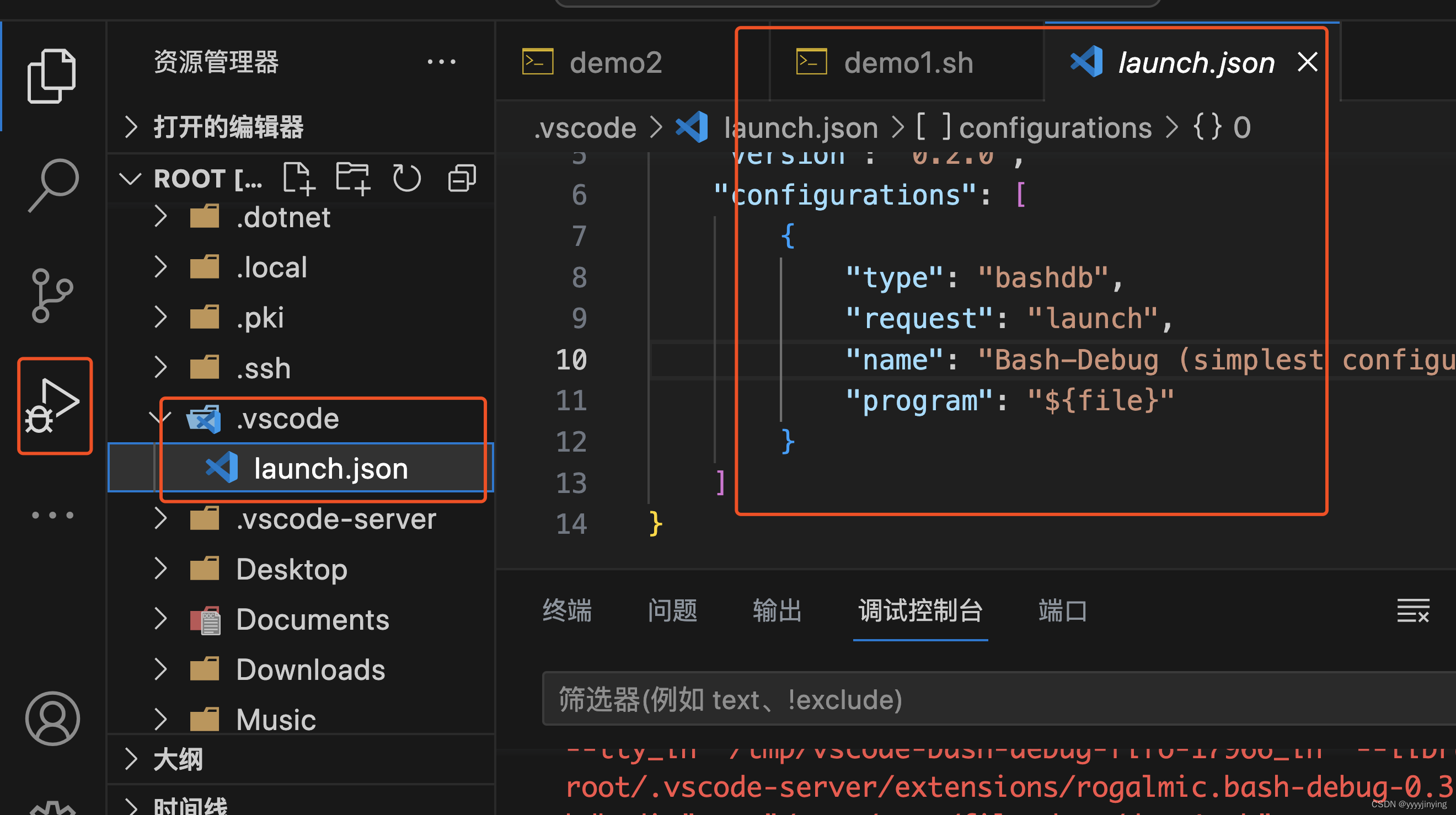
使用Vscode调试shell脚本
在vcode中安装bash dug插件 在vcode中添加launch.json配置,默认就好 参考:http://www.rply.cn/news/73966.html 推荐插件: shellman(支持shell,智能提示) shellcheck(shell语法检查) shell-format(shell格式化)...

OpenAI Function calling
开篇 原文出处 最近 OpenAI 在 6 月 13 号发布了新 feature,主要针对模型进行了优化,提供了 function calling 的功能,该 feature 对于很多集成 OpenAI 的应用来说绝对是一个“神器”。 Prompt 的演进 如果初看 OpenAI 官网对function ca…...

【C语言】字符分类函数、字符转换函数、内存函数
前言 之前我们用两篇文章介绍了strlen、strcpy、stract、strcmp、strncpy、strncat、strncmp、strstr、strtok、streeror这些函数 第一篇文章strlen、strcpy、stract 第二篇文章strcmp、strncpy、strncat、strncmp 第三篇文章strstr、strtok、streeror 今天我们就来学习字…...
Deep Learning With Pytorch - 最基本的感知机、贯序模型/分类、拟合
文章目录 如何利用pytorch创建一个简单的网络模型?Step1. 感知机,多层感知机(MLP)的基本结构Step2. 超平面 ω T ⋅ x b 0 \omega^{T}xb0 ωT⋅xb0 or ω T ⋅ x b \omega^{T}xb ωT⋅xb感知机函数 Step3. 利用感知机进行决策…...
测试工具coverage的高阶使用
在文章Python之单元测试使用的一点心得中,笔者介绍了自己在使用Python测试工具coverge的一点心得,包括: 使用coverage模块计算代码测试覆盖率使用coverage api计算代码测试覆盖率coverage配置文件的使用coverage badge的生成 本文在此基础上…...

安卓监听端口接收消息
文章目录 其他文章监听端口接收消息 建立新线程完整代码 其他文章 下面是我的另一篇文章,是在电脑上发送数据,配合本篇文章,可以实现电脑与手机的局域网通讯。直接复制粘贴就能行,非常滴好用。 点击连接 另外,如果你不…...

「Node」下载安装配置node.js
以下是Node.js的下载、安装和配置的全面教程: 下载 Node.js 打开 Node.js 官方网站:Previous Releases在主页上,您会看到两个版本可供选择:LTS(长期支持版本)和最新版(Current)。如…...
NOIP2014普及组,提高组 比例简化 飞扬的小鸟 答案
比例简化 说明 在社交媒体上,经常会看到针对某一个观点同意与否的民意调查以及结果。例如,对某一观点表示支持的有1498 人,反对的有 902人,那么赞同与反对的比例可以简单的记为1498:902。 不过,如果把调查结果就以这种…...

【Java】使用Apache POI识别PPT中的图片和文字,以及对应的大小、坐标、颜色、字体等
本文介绍如何使用Apache POI识别PPT中的图片和文字,获取图片的数据、大小、尺寸、坐标,以及获取文字的字体、大小、颜色、坐标。 官方文档:https://poi.apache.org/components/slideshow/xslf-cookbook.html 官方文档和网上的资料介绍的很少…...

根据源码,模拟实现 RabbitMQ - 实现消息持久化,统一硬盘操作(3)
目录 一、实现消息持久化 1.1、消息的存储设定 1.1.1、存储方式 1.1.2、存储格式约定 1.1.3、queue_data.txt 文件内容 1.1.4、queue_stat.txt 文件内容 1.2、实现 MessageFileManager 类 1.2.1、设计目录结构和文件格式 1.2.2、实现消息的写入 1.2.3、实现消息的删除…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
