【力扣】496. 下一个更大元素 I <单调栈、模拟>
【力扣】496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。给你两个没有重复元素的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
提示:
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1 0 4 10^4 104
nums1和nums2中所有整数 互不相同
nums1 中的所有整数同样出现在 nums2 中
题解
单调栈+哈希
import java.util.*;public class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {//单调栈Stack<Integer> stack = new Stack<>();//存放结果最终结果,大小和nums1一样int[] result = new int[nums1.length];Arrays.fill(result, -1);//求nums1和nums2的映射关系HashMap<Integer, Integer> map = new HashMap<>();for (int i = 0; i < nums1.length; i++) {// key为数值,value为下标map.put(nums1[i], i);}//先放第一个元素的下标进单调栈stack.add(0);//单调栈遍历数组nums2for (int i = 1; i < nums2.length; i++) {//当前遍历的元素和栈口元素的比较if (nums2[i] <= nums2[stack.peek()]) {stack.push(i);}else {//循环比较while (!stack.isEmpty() && nums2[i] > nums2[stack.peek()]) {if (map.containsKey(nums2[stack.peek()])) {Integer index = map.get(nums2[stack.peek()]);result[index] = nums2[i];}stack.pop();}stack.push(i);}}return result;}
}

暴力:
public class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {int[] result = new int[nums1.length];//遍历nums1的元素,逐个去nums2找for (int i = 0; i < nums1.length; ++i) {//先找到相等的位置int j = 0;while (j < nums2.length && nums2[j] != nums1[i]) {j++;}//继续找右边第一个比它大的int k = j + 1;while (k < nums2.length && nums2[k] < nums2[j]) {k++;}//k < nums2.length说明找到了右边比它大的result[i] = (k < nums2.length) ? nums2[k] : -1;}return result;}
}
相关文章:

【力扣】496. 下一个更大元素 I <单调栈、模拟>
【力扣】496. 下一个更大元素 I nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。给你两个没有重复元素的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。 对于每个 0 < i <…...
Java调用https接口添加证书
使用InstallCert.Java生成证书 /** Copyright 2006 Sun Microsystems, Inc. All Rights Reserved.** Redistribution and use in source and binary forms, with or without* modification, are permitted provided that the following conditions* are met:** - Redistri…...
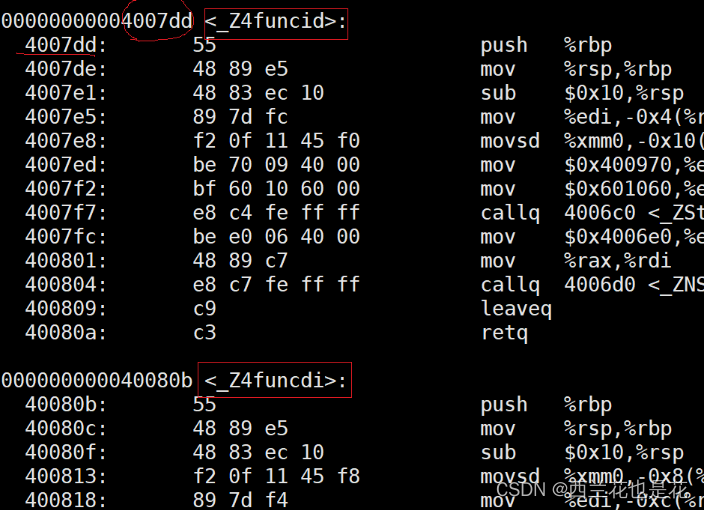
C++入门:函数缺省参数与函数重载
目录 1.函数缺省参数 1.1 缺省参数概念 1.2 缺省参数分类 2.函数重载 2.1 函数重载概念 2.2 C支持函数重载的原理 1.函数缺省参数 1.1 缺省参数概念 缺省参数是声明或定义函数时为函数的参数指定一个缺省值。在调用该函数时,如果没有指定实 参则采用该形参的…...

Android 场景Scene的使用
Scene 翻译过来是场景,开发者提供起始布局和结束布局,就可以实现布局之间的过渡动画。 具体可参考 使用过渡为布局变化添加动画效果 大白话,在 Activity 的各个页面之间切换,会带有过渡动画。 打个比方,使用起来类似…...
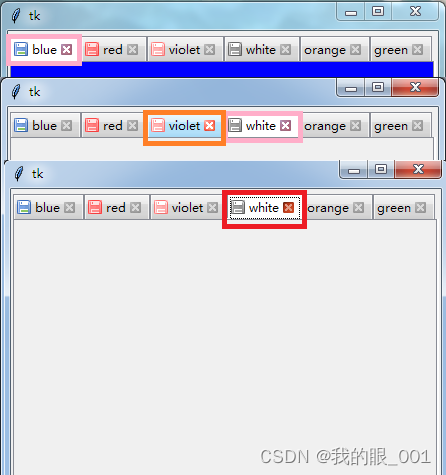
Python tkinter Notebook标签添加关闭按钮元素,及左侧添加存储状态提示图标案例,类似Notepad++页面
效果图展示 粉色框是当前页面,橙色框是鼠标经过,红色框是按下按钮,灰色按钮是其他页面的效果; 存储标识可以用来识别页面是否存储:例如当前页面已经保存用蓝色,未保存用红色,其他页面已经保存用…...
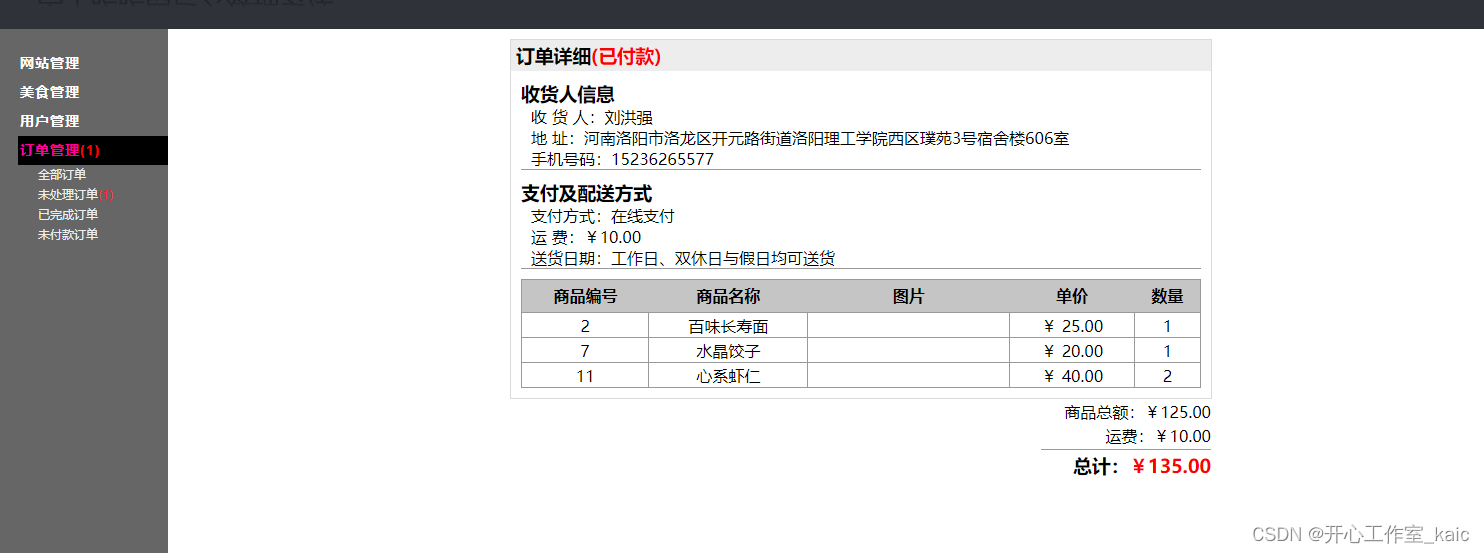
基于web网上订餐系统的设计与实现(论文+源码)_kaic
目录 1绪论 1.1课题研究背景 1.2研究现状 1.3主要内容 1.4本文结构 2网上订餐系统需求分析 2.1系统业务流程分析 2.2消费者用户业务流程分析 2.3商户业务流程分析 2.4管理员用户流程分析消费者用户用例分析 2.5系统用例分析 3网上订餐系统设计 3.1功能概述 3.2订单管理模块概要…...
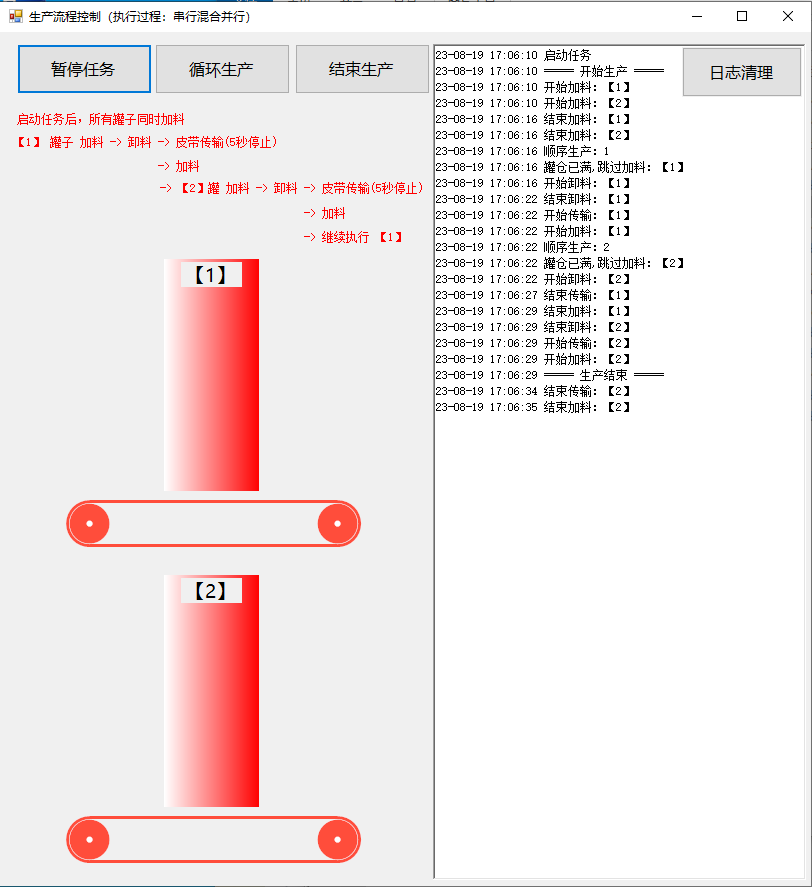
C#生产流程控制(串行,并行混合执行)
开源框架CsGo https://gitee.com/hamasm/CsGo?_fromgitee_search 文档资料: https://blog.csdn.net/aa2528877987/article/details/132139337 实现效果 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37…...
【广州华锐视点】VR线上教学资源平台提供定制化虚拟现实学习内容
虚拟现实(VR)技术的出现为我们提供了一种全新的在线教学方式。由广州华锐视点开发的VR线上教学资源平台,作为一个综合性的学习工具,正在教育领域迅速发展,并被越来越多的教育机构和学生所接受。那么,VR线上…...
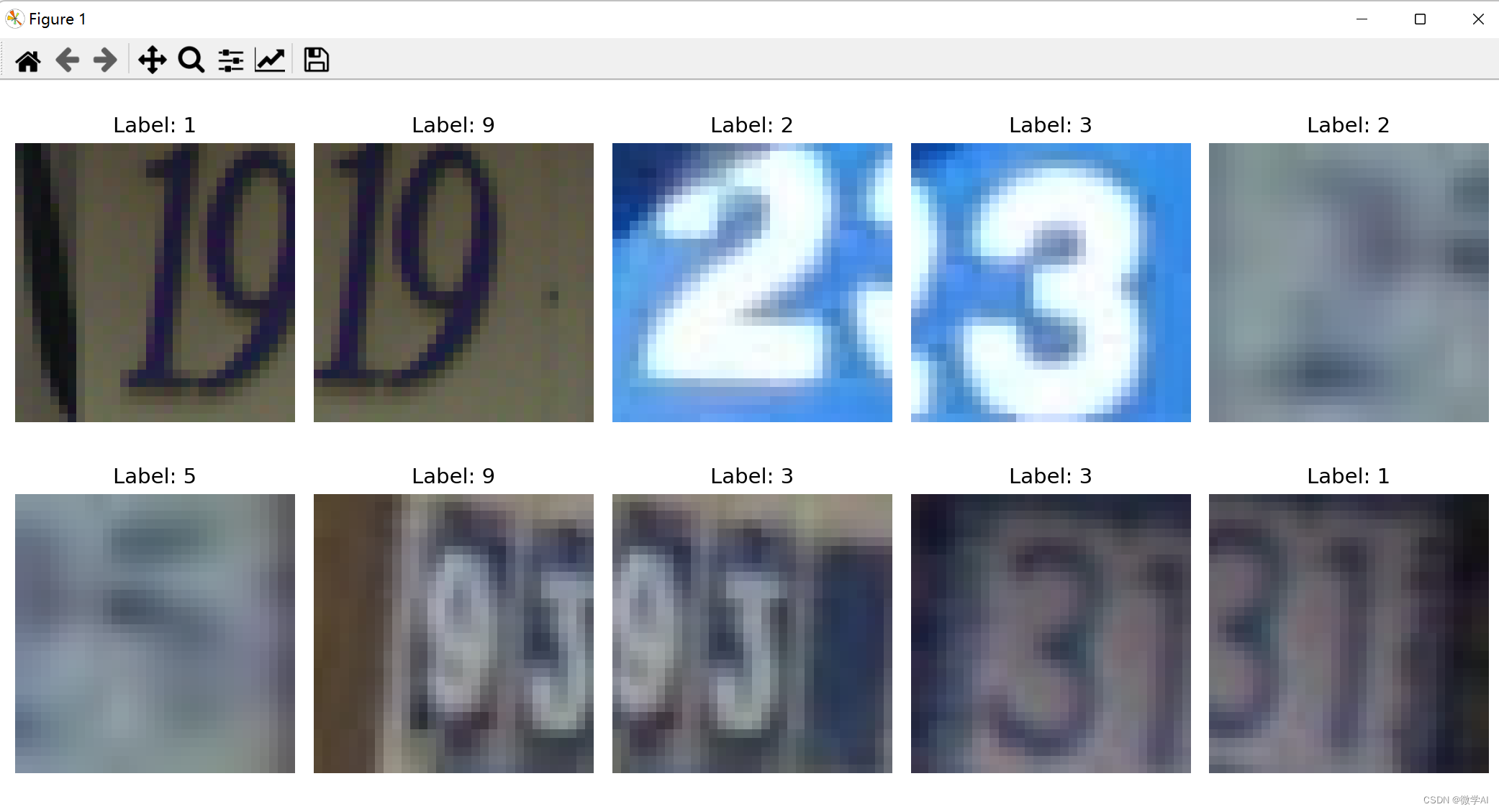
计算机视觉的应用11-基于pytorch框架的卷积神经网络与注意力机制对街道房屋号码的识别应用
大家好,我是微学AI,今天给大家介绍一下计算机视觉的应用11-基于pytorch框架的卷积神经网络与注意力机制对街道房屋号码的识别应用,本文我们借助PyTorch,快速构建和训练卷积神经网络(CNN)等模型,…...

正则表达式:学习使用正则表达式提取网页中的目标数据
使用正则表达式提取网页中的目标数据主要有以下几个步骤: 获取网页内容:首先,你需要使用Python的库(如requests)获取网页的HTML内容。 构建正则表达式:根据你想要提取的目标数据的特征,构建相应…...

最长重复子数组(力扣)动态规划 JAVA
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。 示例 1: 输入:nums1 [1,2,3,2,1], nums2 [3,2,1,4,7] 输出:3 解释:长度最长的公共子数组是 [3,2,1] 。 示例 2: 输…...
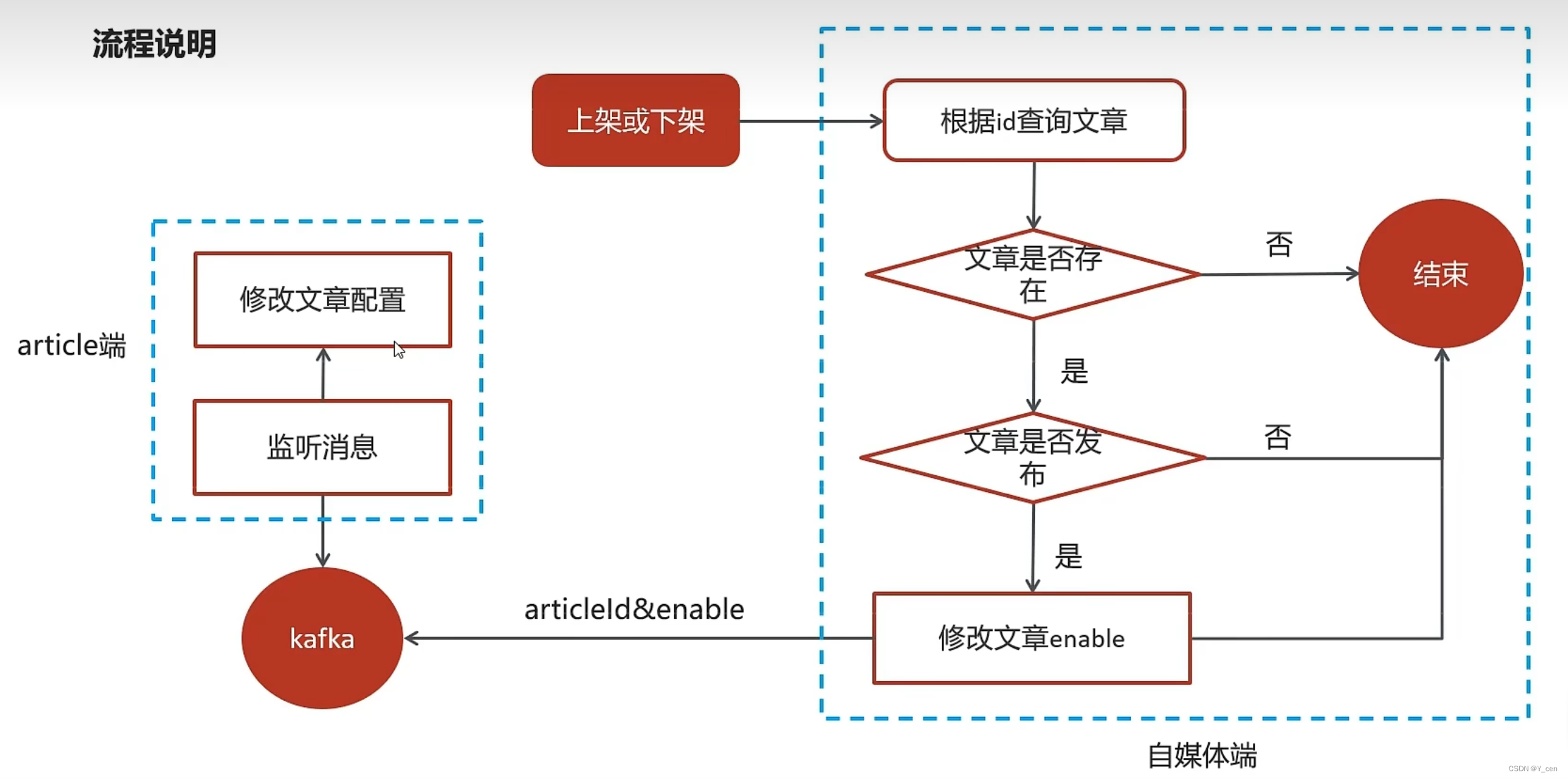
JavaWeb_LeadNews_Day6-Kafka
JavaWeb_LeadNews_Day6-Kafka Kafka概述安装配置kafka入门kafka高可用方案kafka详解生产者同步异步发送消息生产者参数配置消费者同步异步提交偏移量 SpringBoot集成kafka 自媒体文章上下架实现思路具体实现 来源Gitee Kafka 概述 对比 选择 介绍 producer: 发布消息的对象称…...

ATTCK覆盖度97.1%!360终端安全管理系统获赛可达认证
近日,国际知名第三方网络安全检测服务机构——赛可达实验室(SKD Labs)发布最新测试报告,360终端安全管理系统以ATT&CK V12框架攻击技术覆盖面377个、覆盖度97.1%,勒索病毒、挖矿病毒检出率100%,误报率0…...

透视俄乌网络战之一:数据擦除软件
数据擦除破坏 1. WhisperGate2. HermeticWiper3. IsaacWiper4. WhisperKill5. CaddyWiper6. DoubleZero7. AcidRain8. RURansom 数据是政府、社会和企业组织运行的关键要素。数据擦除软件可以在不留任何痕迹的情况下擦除数据并阻止操作系统恢复摧,达到摧毁或目标系统…...

微服务中间件--Nacos
Nacos 1. Nacos入门a.服务注册到Nacosb.Nacos服务分级存储模型c.NacosRule负载均衡d.服务实例的权重设置e.环境隔离 - namespacef.Nacos和Eureka的对比 2. Nacos配置管理a.统一配置管理b.配置热更新c.多环境配置共享 1. Nacos入门 Nacos是阿里巴巴的产品,现在是Spr…...

驱动开发点亮led灯
头文件 #ifndef __HEAD_H__ #define __HEAD_H__#define PHY_LED_MODER 0X50006000 #define PHY_LED_ODR 0X50006014 #define PHY_LED_RCC 0X50000A28 #define PHY_LED_FMODER 0X50007000 #define PHY_LED_FODR 0X50007014#endif驱动代码 #include <linux/init.h> #incl…...

回归预测 | MATLAB实现IPSO-SVM改进粒子群优化算法优化支持向量机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现IPSO-SVM改进粒子群优化算法优化支持向量机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现IPSO-SVM改进粒子群优化算法优化支持向量机多输入单输出回归预测(多指标,多图…...

数学建模之“TOPSIS数学模型”原理和代码详解
一、简介 TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)是一种多准则决策分析方法,用于解决多个候选方案之间的排序和选择问题。它基于一种数学模型,通过比较每个候选方案与理想解和负理想解之间的相…...
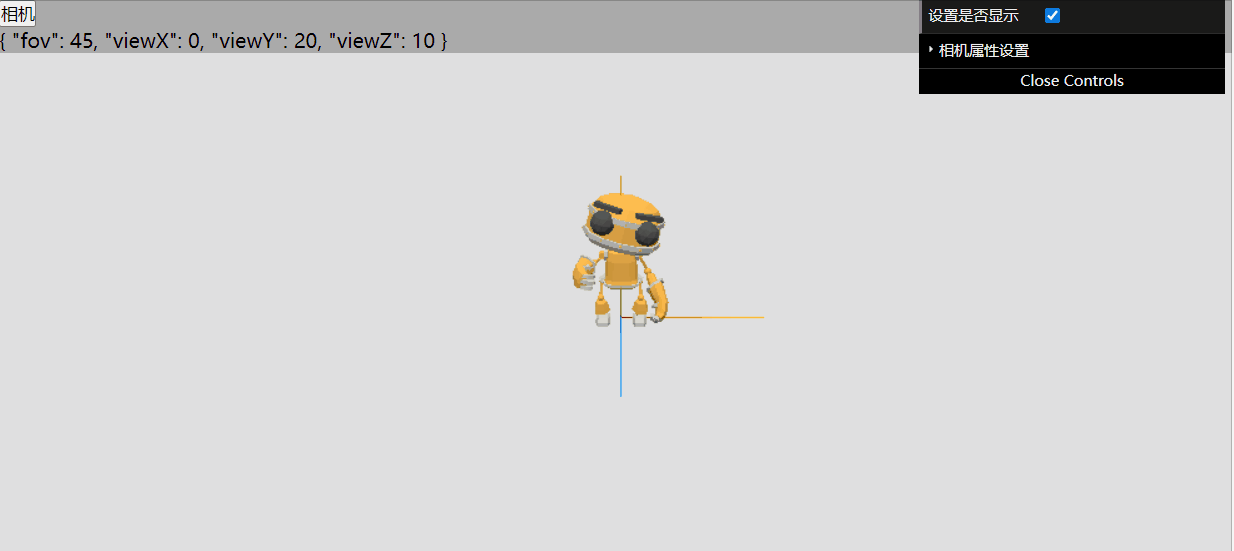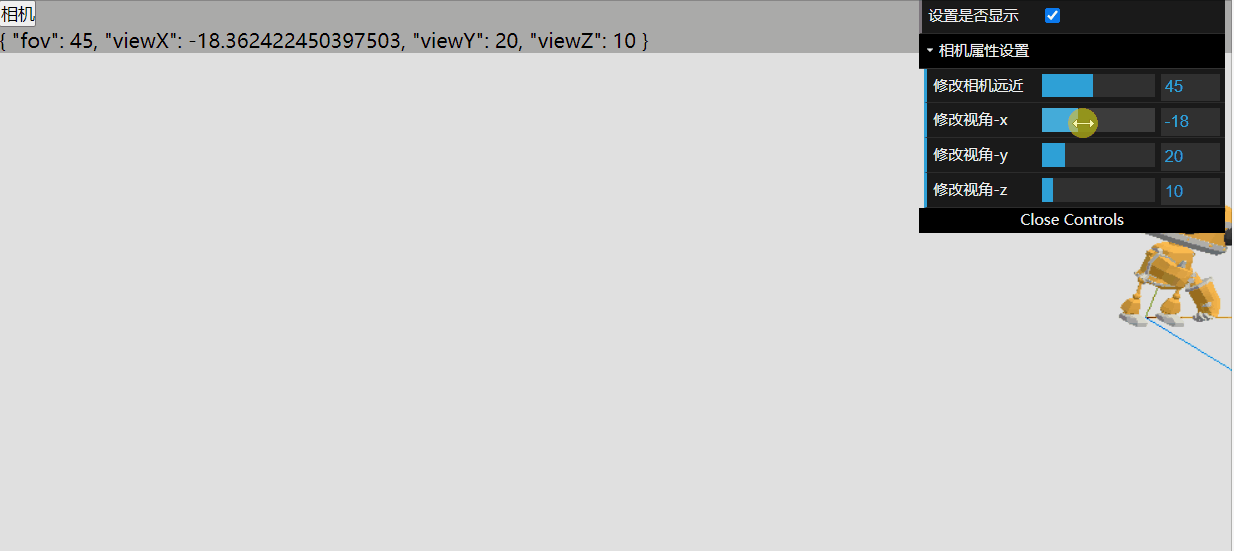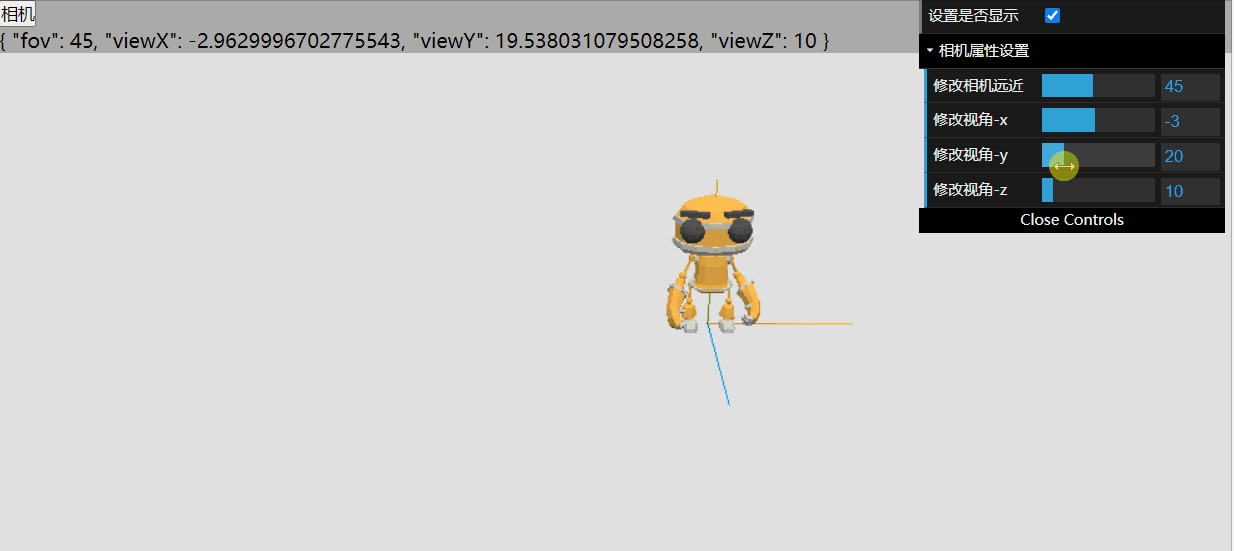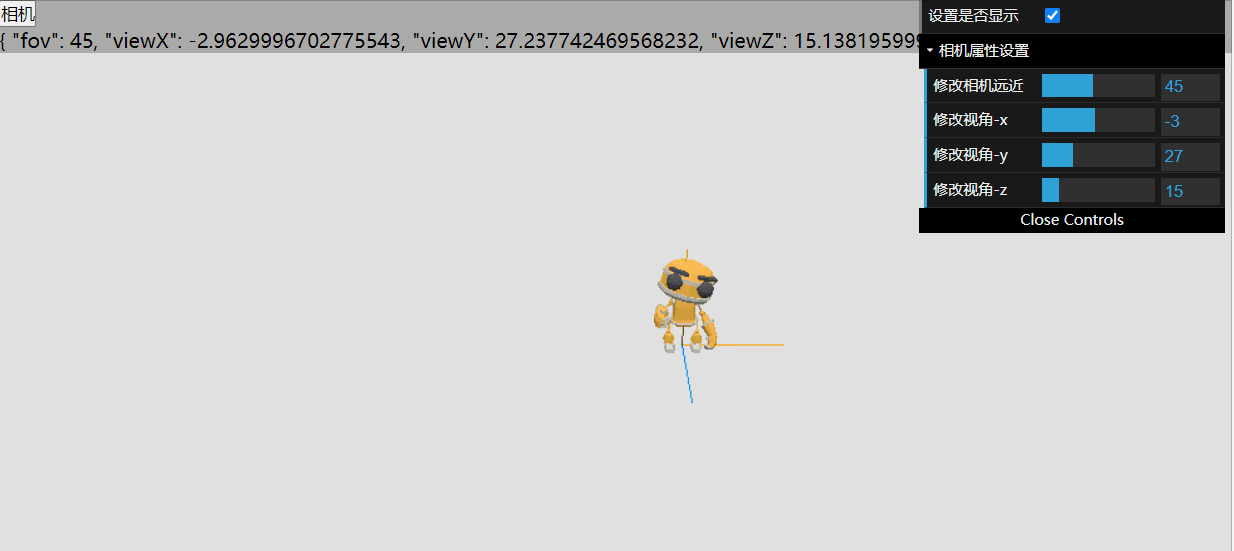
threejs使用gui改变相机的参数
调节相机远近角度 定义相机的配置: const cameraConfg reactive({ fov: 45 }) gui中加入调节fov的方法 const gui new dat.GUI();const cameraFolder gui.addFolder("相机属性设置");cameraFolder.add(cameraConfg, "fov", 0, 100).name(…...
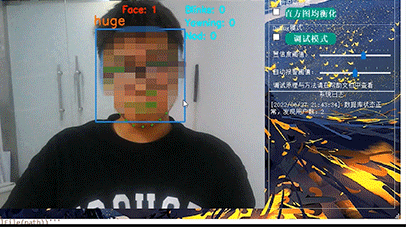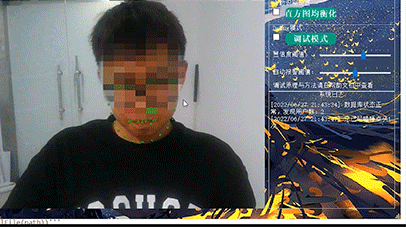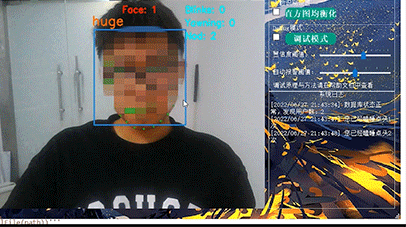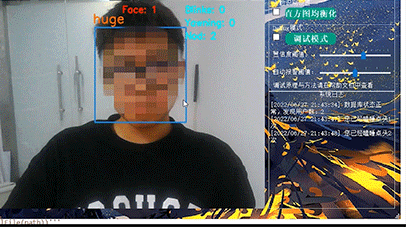
计算机竞赛 图像识别-人脸识别与疲劳检测 - python opencv
文章目录 0 前言1 课题背景2 Dlib人脸识别2.1 简介2.2 Dlib优点2.3 相关代码2.4 人脸数据库2.5 人脸录入加识别效果 3 疲劳检测算法3.1 眼睛检测算法3.3 点头检测算法 4 PyQt54.1 简介4.2相关界面代码 5 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
