97. 约数之和
Powered by:NEFU AB-IN
Link
文章目录
- 97. 约数之和
- 题意
- 思路
- 代码
97. 约数之和
-
题意
假设现在有两个自然数 A和 B,S是 A^B的所有约数之和。
请你求出 S mod 9901的值是多少。 -
思路
ABA^BAB的约数之和为:sumAB=(1+p1+p12+...+p1B×a1)×(1+p2+p22+...+p2B×a2)×...sum_{A^B} = (1 +p_1 + p_1 ^ 2 + ... + p_1^{B×a_1}) × (1 +p_2 + p_2 ^ 2 + ... + p_2^{B×a_2}) × ...sumAB=(1+p1+p12+...+p1B×a1)×(1+p2+p22+...+p2B×a2)×...
为什么最高项是B×aB×aB×a呢,最高项代表ppp这个质因子的个数,一开始AAA有xxx个ppp,那么A3=A×A×AA^3=A×A×AA3=A×A×A就有3x3x3x个ppp-
做法一:等比数列求和 + 快速幂
所以,对于每个质因子,根据等比数列求和公式 (1+p+p2+...+pB×a)=pB×a+1−1p−1(1 +p + p ^ 2 + ... + p^{B×a}) = \frac{p^{B×a+1}-1}{p-1}(1+p+p2+...+pB×a)=p−1pB×a+1−1
那么,对AAA进行质因子分解- pB×a+1p^{B×a+1}pB×a+1用快速幂求
- 1p−1\frac{1}{p-1}p−11用费马小定理求逆元,但必须保证p−1p-1p−1与MODMODMOD互质
- 若p−1p-1p−1与MODMODMOD互质,正常求即可
- 若p−1p-1p−1与MODMODMOD不互质,我们无法求逆元,就换种思路求表达式。因为 p%MOD=1p \% MOD = 1p%MOD=1,(1+p+p2+...+pB×a)%MOD=1+B×a×1=1+B×a(1 +p + p ^ 2 + ... + p^{B×a}) \% MOD= 1 + B×a ×1 = 1 + B×a(1+p+p2+...+pB×a)%MOD=1+B×a×1=1+B×a,所以直接返回1+B×a1 + B×a1+B×a即可
复杂度 O(nlog(n))O(\sqrt{n}log(n))O(nlog(n))
-
做法二:分治 + 快速幂
定义 sum(p,k)=(1+p+p2+...+pk)sum(p, k) = (1 +p + p ^ 2 + ... + p^{k})sum(p,k)=(1+p+p2+...+pk),共k+1k +1k+1项- 当kkk为奇数时,项数为偶数,以下默认k2=⌊k2⌋\frac{k}{2} =\lfloor \frac{k}{2} \rfloor2k=⌊2k⌋
原式=(p0+p1+...+pk2)+(pk2+1+...+pk)=(p0+p1+...+pk2)+pk2+1×(p0+p1+...+pk2)=(1+pk2+1)×sum(p,k2)=(p^0+p^1+...+p^{\frac{k}{2}}) +(p^{\frac{k}{2} +1}+...+p^k) = (p^0+p^1+...+p^{\frac{k}{2}}) + p^{\frac{k}{2} +1} × (p^0+p^1+...+p^{\frac{k}{2}}) = (1 + p^{\frac{k}{2} +1} ) × sum(p, \frac{k}{2})=(p0+p1+...+p2k)+(p2k+1+...+pk)=(p0+p1+...+p2k)+p2k+1×(p0+p1+...+p2k)=(1+p2k+1)×sum(p,2k) - 当kkk为偶数时,转化为奇数情况,sum(p,k)=sum(p,k−1)+pksum(p,k) = sum(p ,k - 1) + p^ksum(p,k)=sum(p,k−1)+pk
复杂度 O(nlog(n)log(n))O(\sqrt{n}log(n)log(n))O(nlog(n)log(n))
- 当kkk为奇数时,项数为偶数,以下默认k2=⌊k2⌋\frac{k}{2} =\lfloor \frac{k}{2} \rfloor2k=⌊2k⌋
-
超时做法三:递推
求(p0+p1+...+pk)(p^0+p^1+...+p^k)(p0+p1+...+pk),可用递推式,ans = ans * p + 1,但此做法会超时
-
-
代码
做法一
/** @Author: NEFU AB-IN* @Date: 2023-02-18 11:22:46* @FilePath: \Acwing\97\97.cpp* @LastEditTime: 2023-02-18 23:11:41*/ #include <bits/stdc++.h> using namespace std; #define int long long #undef int#define SZ(X) ((int)(X).size()) #define ALL(X) (X).begin(), (X).end() #define IOS \ios::sync_with_stdio(false); \cin.tie(nullptr); \cout.tie(nullptr) #define DEBUG(X) cout << #X << ": " << X << '\n' typedef pair<int, int> PII;const int N = 1e5 + 10, INF = 0x3f3f3f3f, MOD = 9901;int quickmod(int a, int b) {a %= MOD;int res = 1;while (b){if (b & 1)res = res * a % MOD;a = a * a % MOD;b = b >> 1;}return res % MOD; }signed main() {IOS;int a, b;cin >> a >> b;if (!a){cout << 0;return 0;}// 质因子分解unordered_map<int, int> mp;for (int i = 2; i <= a / i; ++i){while (a % i == 0){mp[i]++;a /= i;}}if (a > 1)mp[a]++;int ans = 1;auto f = [&](int p, int n) {if ((p - 1) % MOD == 0)return n + 1;int pp = quickmod(p, n + 1);int ny = quickmod(p - 1, MOD - 2);return (pp - 1 + MOD) * ny % MOD;};for (auto [x, cnt] : mp){ans = ans * f(x, cnt * b) % MOD;}cout << ans;return 0; }
做法二
/** @Author: NEFU AB-IN* @Date: 2023-02-18 12:21:32* @FilePath: \Acwing\97\97.1.cpp* @LastEditTime: 2023-02-19 11:36:53*/ #include <bits/stdc++.h> using namespace std; #define int long long #undef int#define SZ(X) ((int)(X).size()) #define ALL(X) (X).begin(), (X).end() #define IOS \ios::sync_with_stdio(false); \cin.tie(nullptr); \cout.tie(nullptr) #define DEBUG(X) cout << #X << ": " << X << '\n' typedef pair<int, int> PII;const int N = 1e5 + 10, INF = 0x3f3f3f3f, MOD = 9901;int quickmod(int a, int b) {a %= MOD;int res = 1;while (b){if (b & 1)res = res * a % MOD;a = a * a % MOD;b = b >> 1;}return res % MOD; }int sum(int p, int k) {if (k == 0)return 1;if (k % 2 == 0)return sum(p, k - 1) % MOD + quickmod(p, k) % MOD;return sum(p, k / 2) % MOD * (1 + quickmod(p, k / 2 + 1)) % MOD; }int main() {IOS;int a, b;cin >> a >> b;if (!a){cout << 0;return 0;}// 质因子分解unordered_map<int, int> mp;for (int i = 2; i <= a / i; ++i){while (a % i == 0){mp[i]++;a /= i;}}if (a > 1)mp[a]++;int ans = 1;for (auto [x, cnt] : mp){ans = ans * sum(x, cnt * b) % MOD;}cout << ans;return 0; }
相关文章:

97. 约数之和
Powered by:NEFU AB-IN Link 文章目录97. 约数之和题意思路代码97. 约数之和 题意 假设现在有两个自然数 A和 B,S是 A^B的所有约数之和。 请你求出 S mod 9901的值是多少。 思路 ABA^BAB的约数之和为:sumAB(1p1p12...p1Ba1)(1p2p22...p2Ba2)...sum_{A^B…...

想和20岁的自己说
男生床头千万不要放卫生纸不要叫自己的女朋友早睡,更不能叫她早起,否则有你好受的。成年人的默契:和异性单独出去旅游,如果没有明确拒绝开一间房,那基本上默认后面会发生的事情不要去考验人性,世上99%的人经…...
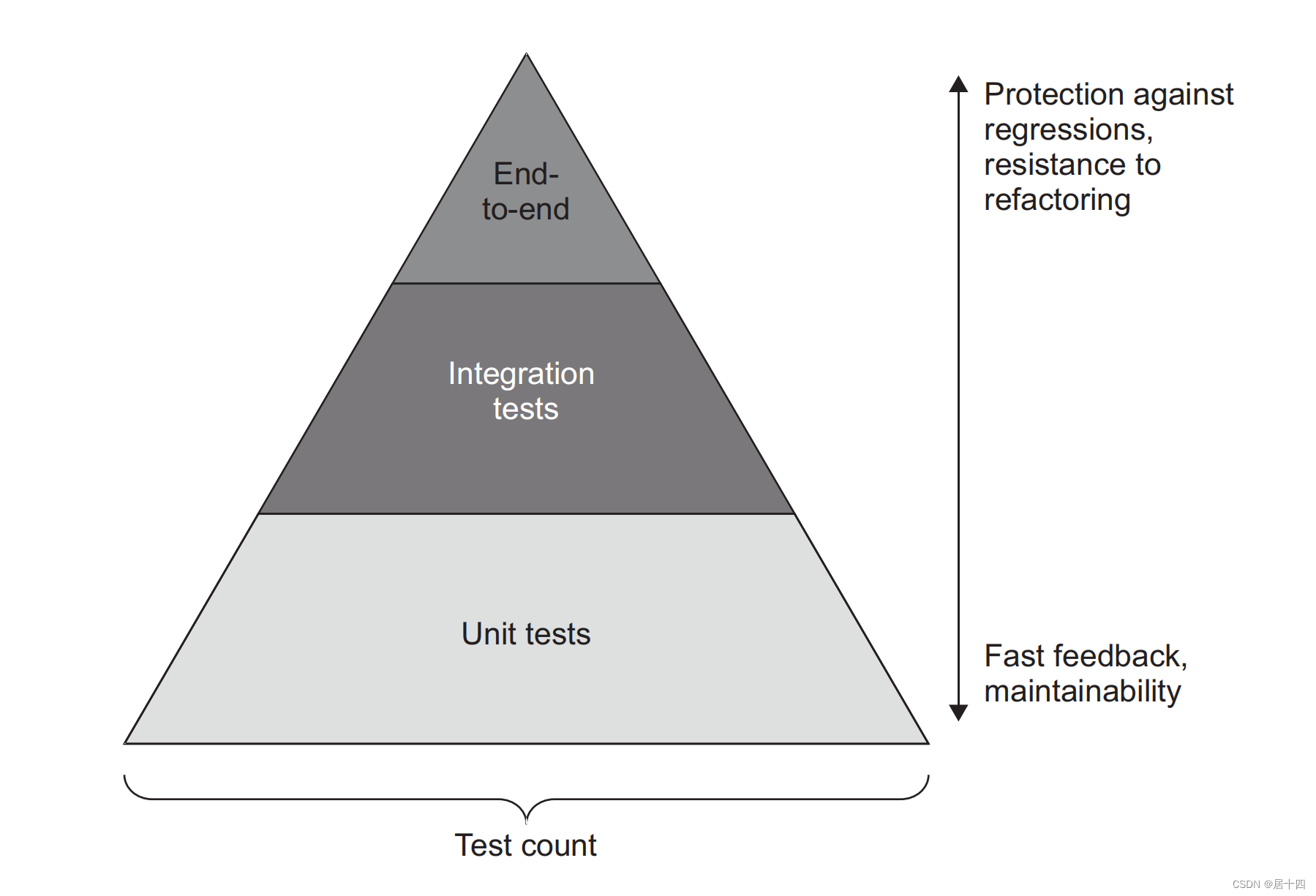
Unit Test and Integration Test
Unit Test and Integration Test Background It is the first time that I try to write an article in English. In the past, I didn’t write test code. Just thinking QA is responsible for testing. As a developer, I don’t need to care about tests. Although I …...

2022年全国职业院校技能大赛(中职组)网络安全竞赛试题(3)
目录 模块A 基础设施设置与安全加固 (本模块20分) 一、项目和任务描述: 假定你是某企业的网络安全工程师,对于企业的服务器系统,根据任务要求确保各服务正常运行,并通过综合运用用户安全管理与密码策略、…...
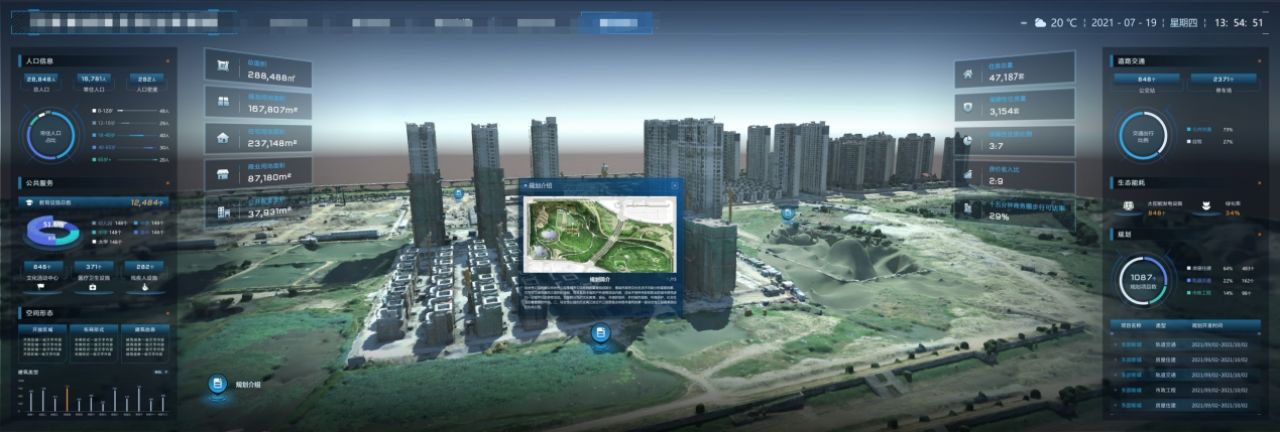
智慧城市应急指挥中心数字化及城市驾驶舱建设方案
目 录 第一章 项目概述 1.1 项目背景 1.2 项目范围 第二章 建设内容 2.1 三维可视化平台 2.1.1 多源数据接入 2.1.2 可视化编排 2.1.3 三维可视化编辑 2.1.4 空间数据可视化 2.1.5 集成框架支持 2.2 可视化场景定制开发 2.2.1 城市驾驶总舱 2.2.2 城市安全分舱 2.…...
HSCSEC 2023 个人练习
😋 大家好,我是YAy_17,是一枚爱好网安的小白。本人水平有限,欢迎各位大佬指点,欢迎关注😁,一起学习 💗 ,一起进步 ⭐ 。⭐ 此后如竟没有炬火,我便是唯一的光。…...
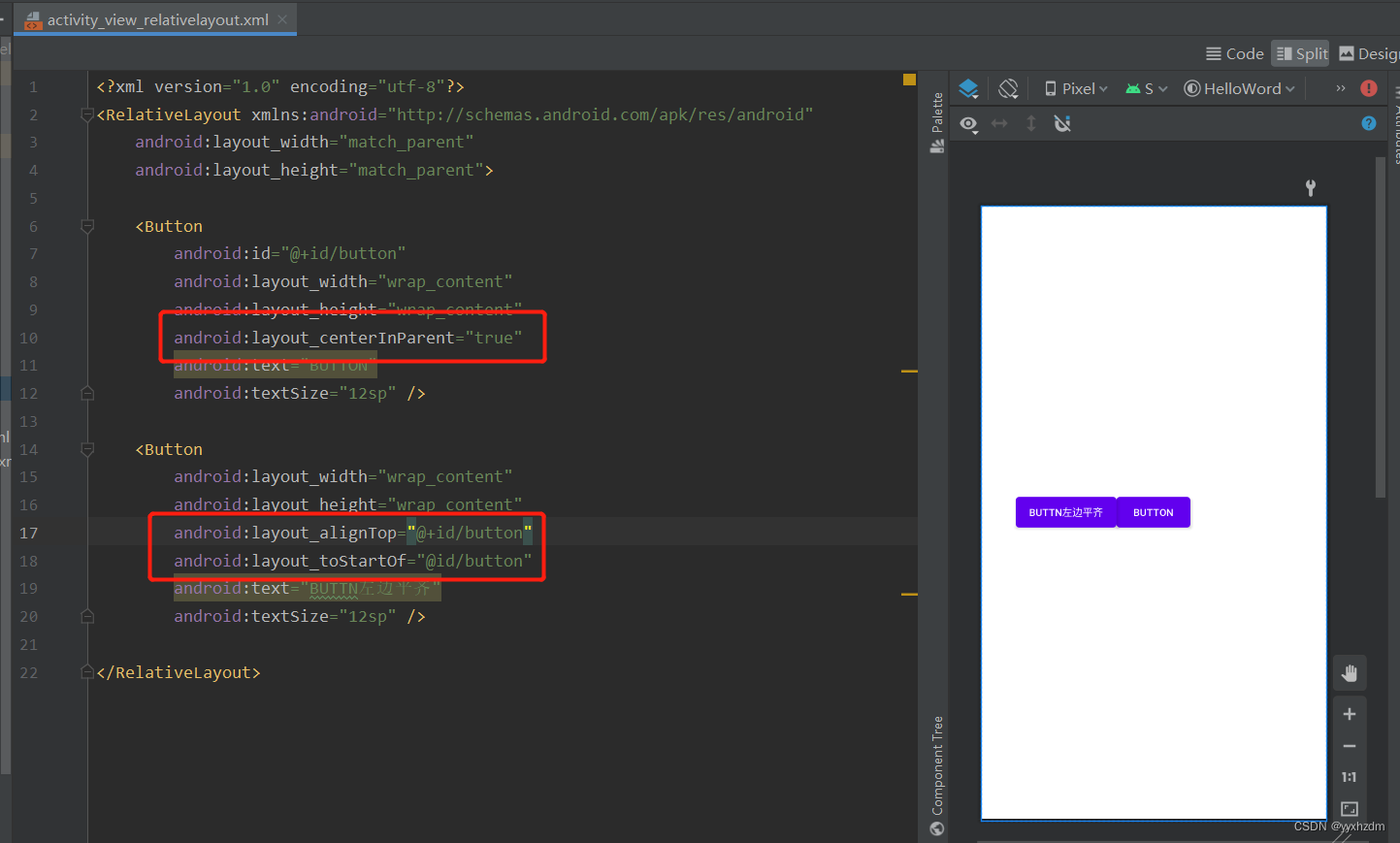
Android 基础知识4-2.7 RelativeLayout(相对布局)
一、RelativeLayout的概述 RelativeLayout(相对布局)是一种根据父容器和兄弟控件作为参照来确定控件位置的布局方式。在很多时候,线性布局还不能满足我们的需求,比如,我们在一行(列)上显示多个控…...

关于云计算,我们问了ChatGPT 10个问题
ChatGPT懂云计算吗?前些天,我们问了ChatGPT(非Plus收费版)一些问题。1. 什么是云计算?2. 云计算行业的护城河是什么?3. 什么是云原生?4. 微软Azure与亚马逊AWS的主要区别是什么?5. 为…...

Netty学习笔记1
Netty学习笔记(一) 在的互联网环境下,分布式系统大行其道,而分布式系统的根基在于网络编程,而 Netty 恰恰是 Java 领域网络编程的王者。如果要致力于开发高性能的服务器程序、高性能的客户端程序,必须掌握…...
)
RISK-V品牌的中国化历程(中)
目录 1.技术优势 出道即巅峰 2.生态布道 品牌根植中国 3.应用场景 加速品牌的商业化运作 生态布道 品牌根植中国 2015年成立非盈利组织RISC-V基金会,目前已吸引全球28个国家327家会员,包括英伟达、联发科、苹果、特斯拉、谷歌、高通、IBM、三星、麻省理…...

2023.02.19 学习周报
文章目录摘要文献阅读1.题目2.摘要3.介绍4.本文贡献5.方法5.1 Local Representation Learning5.2 Global Representation Learning5.3 Item Similarity Gating6.实验6.1 数据集6.2 结果7.结论深度学习1.对偶问题1.1 拉格朗日乘数法1.2 强对偶性2.SVM优化3.软间隔3.1 解决问题3.…...

枚举类的使用方法
一、理解枚举类型 枚举类型是Java 5中新增特性的一部分,它是一种特殊的数据类型,之所以特殊是因为它既是一种类(class)类型却又比类类型多了些特殊的约束,但是这些约束的存在也造就了枚举类型的简洁性、安全性以及便捷性。下面先来看看如何写…...

.NET3.5安装步骤及相关问题。
.NET3.5全称 Microsoft.NETFramework3.5 最新版本-.NET4.8 第一步打开控制面板 windows系统打开控制面板 选择程序 选择.NET3.5安装。 可能会出现问题。 解决方案: 报错代码80240438的常用解决办法: 方法一:检测windows update servic…...

联想M7268激光打印机开机红绿灯双闪报错不打印
故障现象: 一台联想M7268激光打印机开机后电源键、复印键一起双闪,电源键闪红灯、复印键闪绿灯; 检测维修: 根据闪灯故障判断如果无卡纸异常情况下可能是激光器故障,因为以前曾经维修过一台一模一样的机器故障基本相同,先打开机器吧,把硒鼓拿出来先看看有没有卡纸,进纸…...

产品经理知识体系:7.web和app产品需求设计
web和app产品需求设计 思考 笔记 web产品设计 一、交互设计 1.以用户为中心的设计:功能、体验、用户; 将产品功能转化成用户的体验,功能和体验的结合。 2.交互设计模式 交互逻辑 信息结构 信息内容 界面结构 导航设计 二、视觉设计 元素的…...

强化学习概述
一、Modelfree 和 Modelbased Modelfree:不需要理解环境 Modelbased:需要理解环境,并且为环境建立模型 Model-free 中, 机器人只能按部就班, 一步一步等待真实世界的反馈, 再根据反馈采取下一步行动. 而 model-based, 他能通过想象来预判断接…...

NO.1嵌入式入门笔记:常用命令记录
一、前言 Linux文件目录: Linux Shell: 它负责接收用户的输入,根据用户的输入找到其它程序并运行。比如我们输入“ls”并回车时,shell 程序找到“ls”程序并运行,把结果打印出来。Shell有多种实现,我们常用…...

Shell编程
typora-copy-images-to: pictures typora-root-url: pictures 文章目录typora-copy-images-to: pictures typora-root-url: pictures本节课程目标语法和选项语法和选项3. sort工具语法和选项5.tee工具6.diff工具语法和选项7. paste工具8. tr工具语法和选项小试牛刀二、bash的特…...
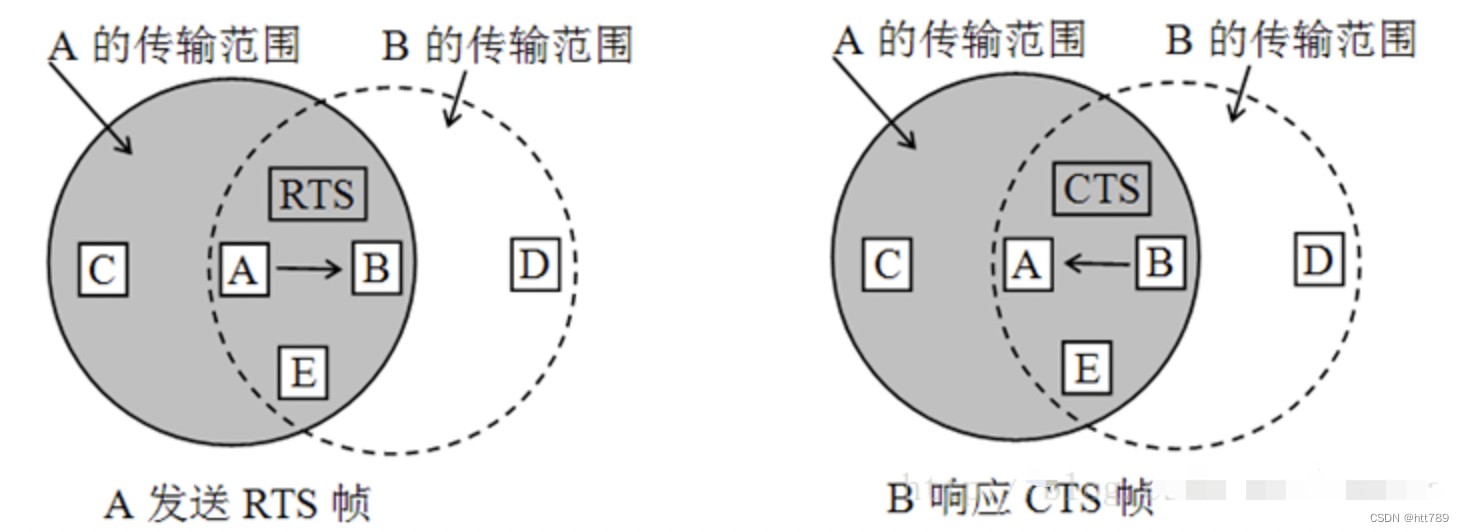
网络模型OSI
网络模型OSI定义模型分布数据封装、解封过程数据链路层1.LLC逻辑链路控制子层(Logic Link Control Sub Layer)2.MAC媒介访问控制子层(Medium Acess Control Sub Layer)CSMA/CARST-CST原理OSI定义 OSI:Open Systems Interconnection Reference Model,开放…...
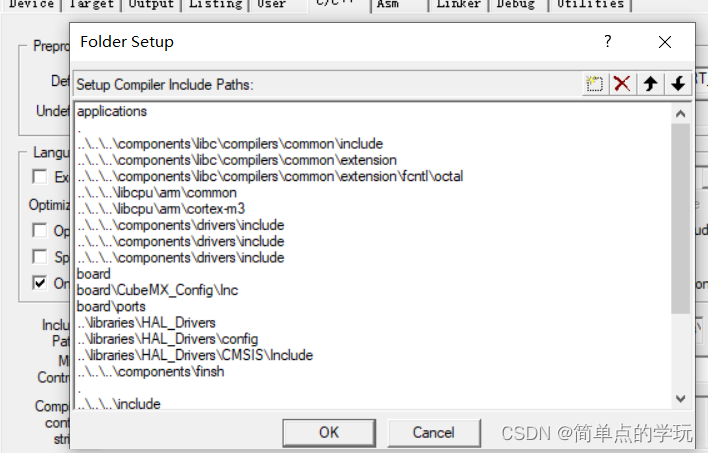
RT-Thread初识学习-01
1. RT-Thread 简介 1.1 RT-Thread 是什么 据不完全统计,世界有成千上万个 RTOS(Real-time operating system,实时操作系统),RT-Thread 就是其中一个优秀的作品。 RT-Thread 内核的第一个版本是熊谱翔先生在 2006 年…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
