【1792. 最大平均通过率】
来源:力扣(LeetCode)
描述:
一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] = [passi, totali] ,表示你提前知道了第 i 个班级总共有 totali 个学生,其中只有 passi 个学生可以通过考试。
给你一个整数 extraStudents ,表示额外有 extraStudents 个聪明的学生,他们 一定 能通过任何班级的期末考。你需要给这 extraStudents 个学生每人都安排一个班级,使得 所有 班级的 平均 通过率 最大 。
一个班级的 通过率 等于这个班级通过考试的学生人数除以这个班级的总人数。平均通过率 是所有班级的通过率之和除以班级数目。
请你返回在安排这 extraStudents 个学生去对应班级后的 最大 平均通过率。与标准答案误差范围在 10-5 以内的结果都会视为正确结果。
示例 1:
输入:classes = [[1,2],[3,5],[2,2]], extraStudents = 2
输出:0.78333
解释:你可以将额外的两个学生都安排到第一个班级,平均通过率为 (3/4 + 3/5 + 2/2) / 3 = 0.78333 。
示例 2:
输入:classes = [[2,4],[3,9],[4,5],[2,10]], extraStudents = 4
输出:0.53485
提示:
- 1 <= classes.length <= 105
- classes[i].length == 2
- 1 <= passi <= totali <= 105
- 1 <= extraStudents <= 105
方法:优先队列
思路与算法
由于班级总数不会变化,因此题目所求「最大化平均通过率」等价于「最大化总通过率」。设某个班级的人数为 total,其中通过考试的人数为 pass,那么给这个班级安排一个额外通过考试的学生,其通过率会增加:
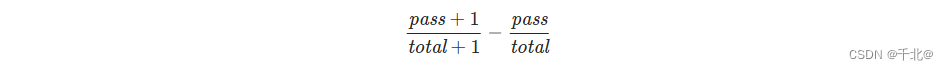
我们会优先选择通过率增加量最大的班级,这样做的正确性在于给同一个班级不断地增加安排的学生数量时,其增加的通过率是单调递减的,即:
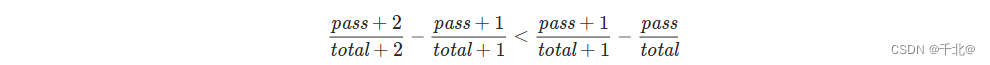
因此当以下条件满足时,班级 j 比班级 i 优先级更大:
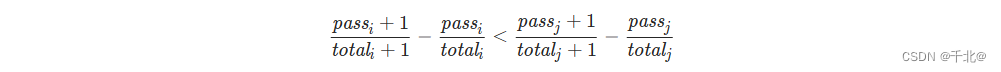
化简后可得:
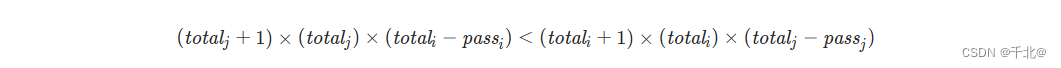
我们按照上述比较规则将每个班级放入优先队列中,进行 extraStudents 次操作。每一次操作,我们取出优先队列的堆顶元素,令其 pass 和 total 分别加 1,然后再放回优先队列。
最后我们遍历优先队列的每一个班级,计算其平均通过率即可得到答案。
代码:
class Solution {
public:struct Ratio {int pass, total;bool operator < (const Ratio& oth) const {return (long long) (oth.total + 1) * oth.total * (total - pass) < (long long) (total + 1) * total * (oth.total - oth.pass);}};double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {priority_queue<Ratio> q;for (auto &c : classes) {q.push({c[0], c[1]});}for (int i = 0; i < extraStudents; i++) {auto [pass, total] = q.top();q.pop();q.push({pass + 1, total + 1});}double res = 0;for (int i = 0; i < classes.size(); i++) {auto [pass, total] = q.top();q.pop();res += 1.0 * pass / total;}return res / classes.size();}
};
执行用时:680 ms, 在所有 C++ 提交中击败了94.29%的用户
内存消耗:85.9 MB, 在所有 C++ 提交中击败了79.05%的用户
复杂度分析
时间复杂度:O((n+m)logn) 或 O(n+mlogn),其中 n 为classes 的长度,m 等于 extraStudents。每次从优先队列中取出或者放入元素的时间复杂度为 O(logn),共需操作 O(n+m) 次,故总复杂度为 O((n+m)logn)。堆化写法的时间复杂度为 O(n+mlogn)。
空间复杂度:O(n) 或 O(1)。使用优先队列需要用到 O(n) 的空间,但若直接在 classes 上原地堆化,则可以做到 (1) 额外空间。
author:LeetCode-Solution
相关文章:
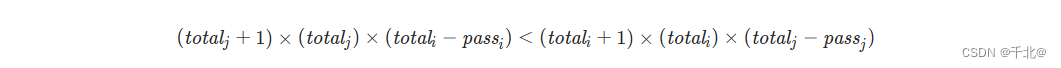
【1792. 最大平均通过率】
来源:力扣(LeetCode) 描述: 一所学校里有一些班级,每个班级里有一些学生,现在每个班都会进行一场期末考试。给你一个二维数组 classes ,其中 classes[i] [passi, totali] ,表示你…...

言简意赅+图解 函数传参问题(传值、传地址 500字解决战斗)
1、传值 2、传地址 不论是传值,还是传地址,形参都是对于实参的一份拷贝 下图为按值传递进行交换: 形参left拷贝一块新空间,形参right拷贝一块新空间 下图为按指针传递进行交换 形参left拷贝一块新的空间,形参right…...
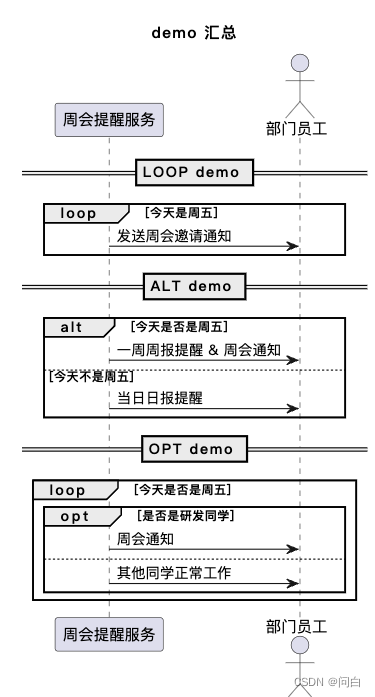
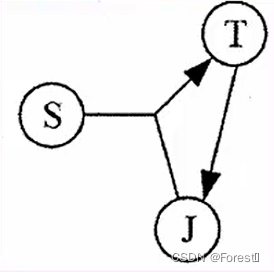
UML-时序图以及PlantUML绘制
介绍 时序图(Sequence Diagram),又名序列图、循序图,是一种UML交互图。它通过描述对象之间发送消息的时间顺序显示多个对象之间的动态协作。它可以表示用例的行为顺序,当执行一个用例行为时,其中的每条消息…...
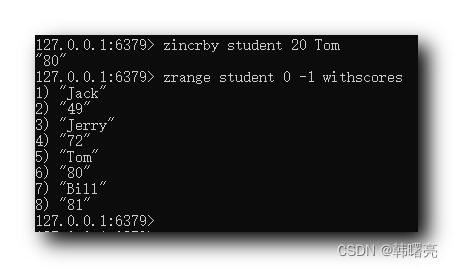
【Redis】Redis 有序集合 Zset 操作 ( 简介 | 查询操作 | 增加操作 | 删除操作 | 修改操作 )
文章目录一、有序集合 Zset二、查询操作1、查询 Zset 所有数据2、查询 Zset 所有数据和评分3、查询指定评分范围的 Zset 数据4、查询指定评分范围的 Zset 数据并从大到小排序5、统计指定评分范围的 Zset 数据个数6、查询指定元素在 Zset 有序集合中的排名三、增加操作1、向 Red…...
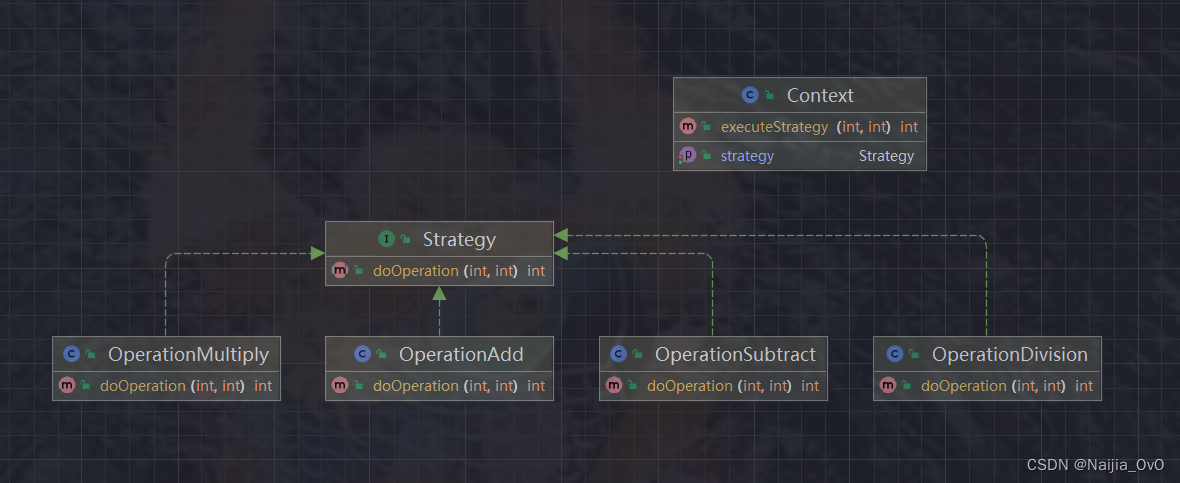
Java特性之设计模式【策略模式】
一、策略模式 概述 在策略模式(Strategy Pattern)中,一个类的行为或其算法可以在运行时更改。这种类型的设计模式属于行为型模式 在策略模式中,我们创建表示各种策略的对象和一个行为随着策略对象改变而改变的 context 对象。策略…...

IR-CUT 保证摄像机成像效果的滤镜
IR-CUT双滤镜是指在摄像头镜头组里内置了一组滤镜,当镜头外的红外感应点侦测到光线的强弱变化后,内置的IR-CUT自动切换滤镜能够根据外部光线的强弱随之自动切换,使图像达到最 佳效果。也就是说,在白天或黑夜下,双滤光片…...

openpnp - 普通航空插头和PCB的连接要使用线对板连接器
文章目录openpnp - 普通航空插头和PCB的连接要使用线对板连接器概述改进实际效果总结ENDopenpnp - 普通航空插头和PCB的连接要使用线对板连接器 概述 和同学讨论问题, 准备将航空插头连接到PCB上. 航空插头选用GX12-4公头, 拧到开孔的铁板上. 然后航空插头公头再与PCB连接. 铁…...
Python3 错误和异常实例及演示
作为 Python 初学者,在刚学习 Python 编程时,经常会看到一些报错信息,在前面我们没有提及,这章节我们会专门介绍。 Python 有2种错误很容易辨认:语法错误和异常。 Python assert(断言)用于判断…...

Android 9.0第三方app根据包名设置为横屏显示
1.概述 在android9.0的系统rom定制化开发中,在某些横屏的设备比如平板电脑,tv智能电视,广告机等等设备中,通常系统是默认横批显示的,但是在安装一些竖屏app的时候, 就会旋转为竖屏,这个时候操作app也不方便,所以产品需求要求竖屏也需要根据包名横屏显示出来,这就需要在…...

MySQL会导致索引失效的情况与解决索引失效的方法
什么情况会导致索引失效 索引失效也是慢查询的主要原因之一,常见的导致索引失效的情况有下面这些: 1.使用 SELECT * 进行查询;2.创建了组合索引,但查询条件未准守最左匹配原则;3.在索引列上进行计算、函数、类型转换等操作;4.以 % 开头的 L…...

使用nginx单独部署Vben应用
前言 本文主要介绍Vben使用nginx单独部署的方式,其实前端发展到现在已经不是当年的jsp,asp必须要和后端一起部署了。单独部署调试的工具也很多,比如vue-cli-service 和 Vben中用到的vite ,当然这些我们一般用在开发的工程中。正式…...
ES6新特性详解
文章目录1. let和const1.1 let声明变量1.2 const声明常量2. 模板字符串3. 解构赋值3.1 数组的解构赋值3.2 对象的解构赋值4. 函数扩展4.1 参数默认值4.2 剩余参数4.3 箭头函数5. 对象扩展5.1 对象简写5.2 属性名表达式5.3 扩展运算符6. Symbol7. Iterator和Generator7.1 Iterat…...
Ubuntu下安装 ntfs-3g
目录1.FAT32、NTFS和exFAT2.ubuntu 安装 ntfs-3g2.1 直接安装2.2 源码安装1.FAT32、NTFS和exFAT U盘在格式化的时候都会有三种格式分别是FAT32、NTFS和exFAT。 FAT32格式 FAT32格式硬盘分区的最大容量为2TB,虽然U盘做不到,但是现在1xTB硬盘都有了&…...

【专业认知】抖音就业 / 保研北大教育学 / 留学南加州EE / 微软就业
2023.2.18 一. 周金辉学长分享——本科经验分享 0 简介 计算机农大本硕 硕士毕业后在抖音公司工作 1 行业前景:计算机专业能做什么? 1.1 计算机行业发展路线 远古时代: 二战开始,计算机技术发展,出现互联网 包…...

【算法题】2 的 n 次幂的背后
前言: 说实话,真的不爱写算法题相关的文章了,觉得没啥意义,但是对这种比较好玩并且简单,学会了就能很好提高算法效率的文章,还是要写一写,不哭不哭,你不会不是你的错,只是…...

【人工智能AI】一、NoSQL 企业级基础入门《NoSQL 企业级基础入门与进阶实战》
写一篇介绍什么是NoSQL的技术文章,分5个章节,每个章节细分到3级目录,重点介绍一下优缺点,适用场景,未来发展趋势等。 一、NoSQL简介 1.1 什么是NoSQL NoSQL(Not only SQL),意思是“…...

Ubuntu安装opencv库3.4.10,并在cmake工程中引入opencv库
Windows下安装不同,Ubuntu安装OpenCV库时,需要事先安装依赖,而且不同OpenCV库所需的依赖可能会有所不同,下面的依赖亲测 3.4.10 和 4.5.5版本的有效,但是4.6以上版本安装可能会报错。 参考链接:https://bl…...
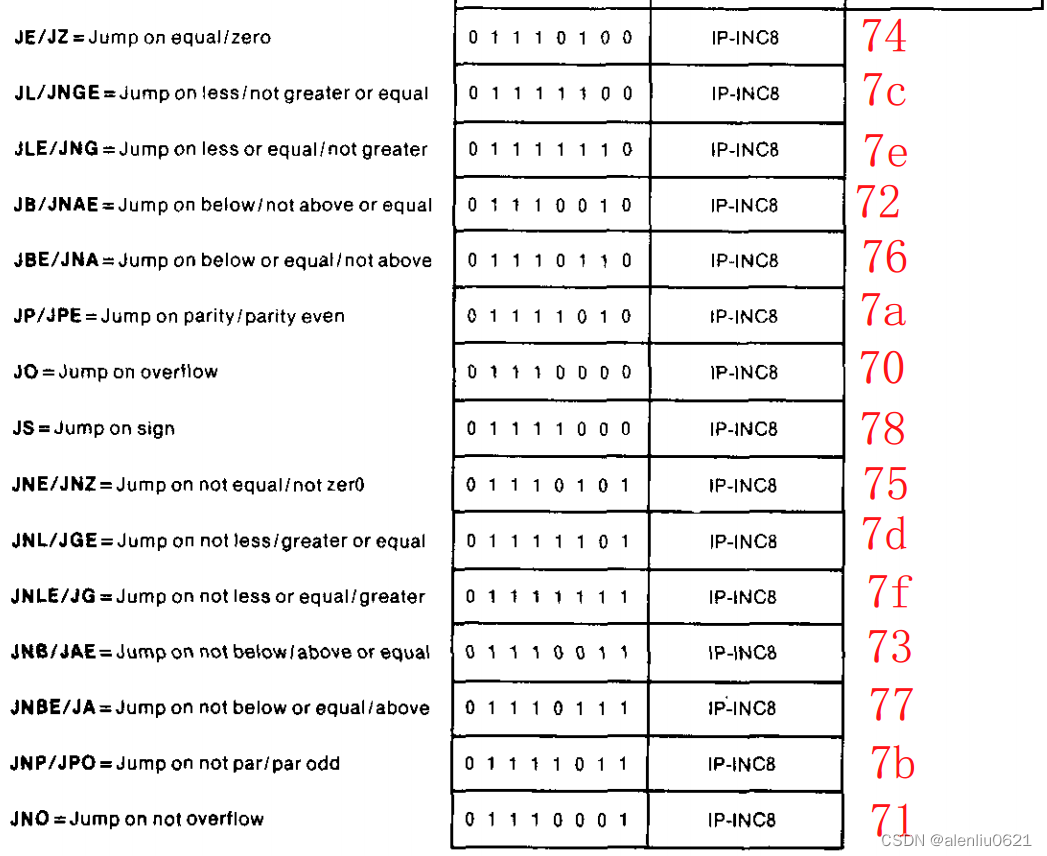
实现8086虚拟机(四)——mov 和 jmp 指令解码
文章目录mov 指令解码jmp 指令解码这篇文章举例来讲讲 mov 指令和 jmp 指令解码函数的实现,其他的指令解码函数都与这些类似。mov 指令解码 以 mov 指令中的一类:寄存器/内存 到/从 寄存器,来详细说明解码函数的实现。 机器指令格式如下&am…...
数据库技术-函数依赖、键与约束、范式
一、函数依赖 给定一个x,能唯一确定一个Y,就称x确定Y,或者说Y依赖于x,例如YX*X函数。 函数依赖又可扩展以下两种规则: 部分函数依赖:A可确定C,(A,B)也可确定C,(A,B)中的一部分(即A)可以确定C&a…...
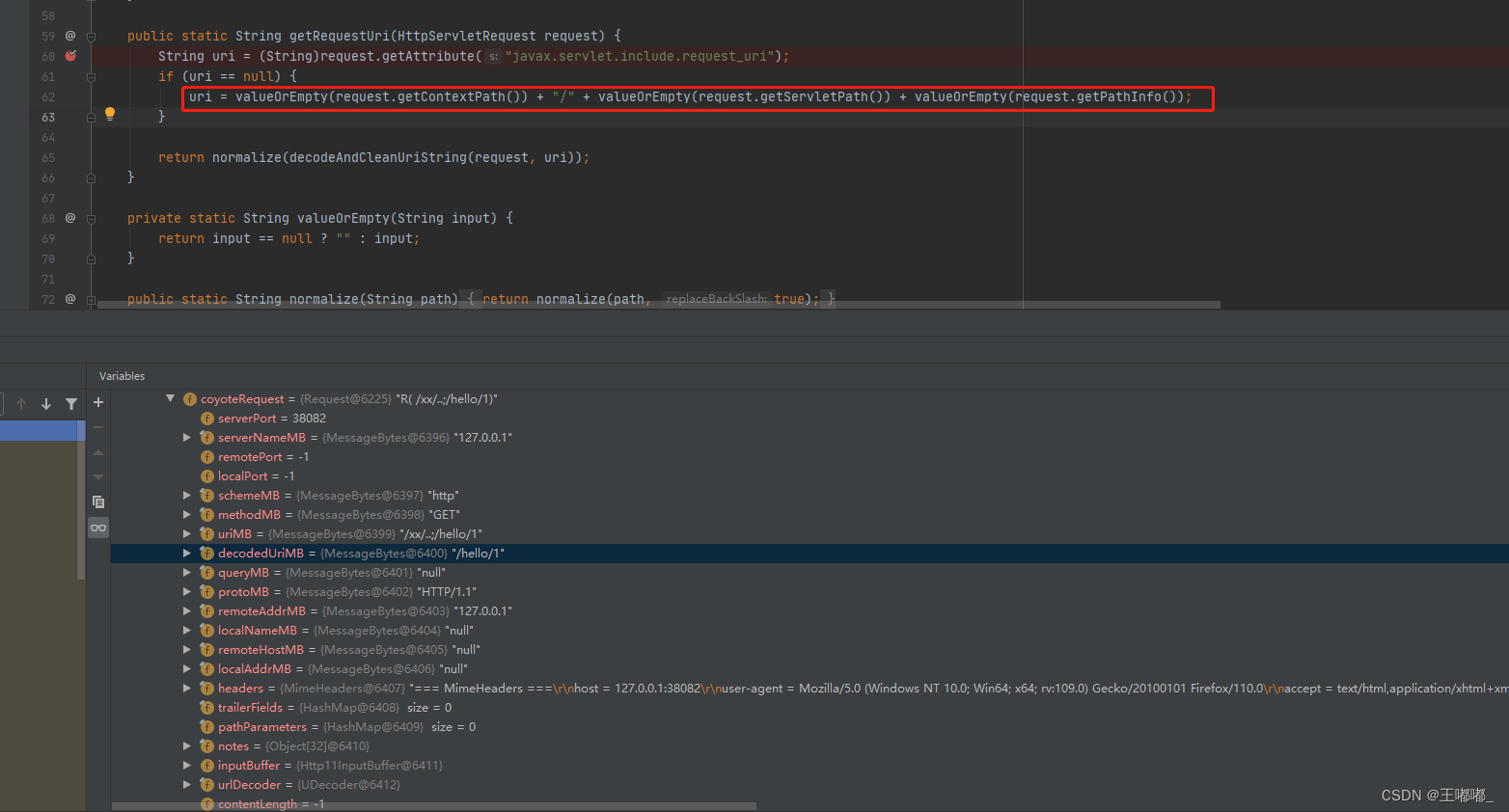
shiro CVE-2020-1957
0x00 前言 在之前只是单纯的复现了漏洞,没有记笔记,所以补充了这篇分析笔记。 影响版本:shiro < 1.5.2 0x01 环境搭建 环境用的是:https://github.com/lenve/javaboy-code-samples/tree/master/shiro/shiro-basic 0x02 漏…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
