2023牛客暑期多校训练营9 B.Semi-Puzzle: Brain Storm
文章目录
- 题目大意
- 题解
- 求解
- 回溯
- 参考代码
题目大意
给定两个数 a , m a,m a,m ,求满足 a u ≡ u ( m o d m ) a^u \equiv u (mod\ \ m) au≡u(mod m) 的一个解。
( 1 ≤ a , m ≤ 1 0 9 , 0 ≤ u ≤ 1 0 18 ) (1\leq a,m \leq10^9 ,0\leq u\leq 10^{18}) (1≤a,m≤109,0≤u≤1018)
题解
参考了讨论区 https://blog.nowcoder.net/n/576f9463036346f0a0fb04fee50fac75 的方法
求解
考虑使用欧拉定理,考虑 b > = ϕ p b>=\phi_p b>=ϕp的情况。
a u ≡ { a u % ϕ m g c d ( a , u ) = 1 a u % ϕ i + ϕ m g c d ( a , u ) ! = 1 ( m o d m ) a^u\equiv\begin{cases}a^{u\% \phi_m }&gcd(a,u)=1\\a^{u\% \phi_i+\phi_m}& gcd(a,u)!=1\end{cases}(mod \ m) au≡{au%ϕmau%ϕi+ϕmgcd(a,u)=1gcd(a,u)!=1(mod m)
定义 d = u % ϕ m d=u\%\phi_m d=u%ϕm 或 u % ϕ m + ϕ m u\%\phi_m+\phi_m u%ϕm+ϕm 和
k ∗ ϕ p + d = u ( k > = 0 ) k*\phi_p+d=u(k>=0) k∗ϕp+d=u(k>=0)
则原式可以转化为 a d ≡ d + k ∗ ϕ m ( m o d m ) a^d \equiv d+k*\phi_m (mod\ m) ad≡d+k∗ϕm(mod m)
移项可以得到 a d − d ≡ k ∗ ϕ m ( m o d m ) a^d-d\equiv k*\phi_m(mod\ m) ad−d≡k∗ϕm(mod m)
ϕ m ∗ x 1 + m ∗ y 1 ≡ g c d ( ϕ m , m ) ( m o d m ) \phi_m*x1+m*y1\equiv gcd(\phi_m,m) (mod \ m) ϕm∗x1+m∗y1≡gcd(ϕm,m)(mod m) 是一个已知有解的同余方程
回到上一个方程想要得到解 k k k ,显然要满足 a d − d = x ∗ g c d ( m , ϕ m ) , ( x > 0 ) a^d-d=x *gcd(m,\phi_m),(x>0) ad−d=x∗gcd(m,ϕm),(x>0)
也就是 a d ≡ d ( m o d g c d ( m , ϕ m ) ) a^d \equiv d (mod \ gcd(m,\phi_m)) ad≡d(mod gcd(m,ϕm))。
重新得到了题目,但是模数缩小了,因此我们想到了递归,直到模数为 1 1 1 时直接推出答案。
回溯
假设我们已经得到了最后一组解 d = 0 d=0 d=0 ,
求解同余方程 a d − d ≡ k ∗ ϕ m ( m o d m ) a^d-d\equiv k*\phi_m(mod\ m) ad−d≡k∗ϕm(mod m),使用扩展欧几里得定理,推出 x 1 x1 x1 的值,
k = x 1 ∗ a d − d g c d ( m , ϕ m ) % m o d k=x1*\frac{a^d-d}{gcd(m,\phi_m)}\%mod k=x1∗gcd(m,ϕm)ad−d%mod
由于 a d a^d ad 超出范围,根据 a b % ( b ∗ c ) = a % ( b ∗ c ) b \frac{a}{b}\%(b*c)=\frac{a\%(b*c)}{b} ba%(b∗c)=ba%(b∗c)得出
k = x 1 ∗ ( a d − d ) % m / ϕ m k=x1*(a^d-d)\%m/\phi_m k=x1∗(ad−d)%m/ϕm 。
再利用 k ∗ ϕ p + d = u k*\phi_p+d=u k∗ϕp+d=u,得出结果即可。
参考代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll phi(ll x)
{ll ans=x;for(int i=2;i*i<=x;i++){if(x%i==0)ans=ans/i*(i-1);while(x%i==0)x/=i;}if(x!=1)ans=ans/x*(x-1);return ans;
}
ll ksm(ll a,ll b,ll p)
{ll res=1;while(b){if(b&1)res=res*a%p;a=a*a%p;b>>=1;}return res;
}
ll exgcd(ll a,ll b,ll &x,ll &y)
{if(!b){x=1,y=0;return a;}ll k=exgcd(b,a%b,y,x);y-=a/b*x;return k;
}
int n,T;
ll a,m;
ll work(ll a,ll p) //递归求解
{if(p==1)return 0;ll m=phi(p);ll b=work(a,__gcd(m,p))+m;ll x,y;ll d=exgcd(m,p,x,y);ll k=(((x*(ksm(a,b,p)-b+p))%p+p)%p/d); //回溯求值return k*m+b;
}
int main()
{cin>>T;while(T--){scanf("%lld%lld",&a,&m);printf("%lld\n",work(a,m));}
}
相关文章:

2023牛客暑期多校训练营9 B.Semi-Puzzle: Brain Storm
文章目录 题目大意题解求解回溯 参考代码 题目大意 给定两个数 a , m a,m a,m ,求满足 a u ≡ u ( m o d m ) a^u \equiv u (mod\ \ m) au≡u(mod m) 的一个解。 ( 1 ≤ a , m ≤ 1 0 9 , 0 ≤ u ≤ 1 0 18 ) (1\leq a,m \leq10^9 ,0\leq u\leq 10^{18}) (1≤a…...
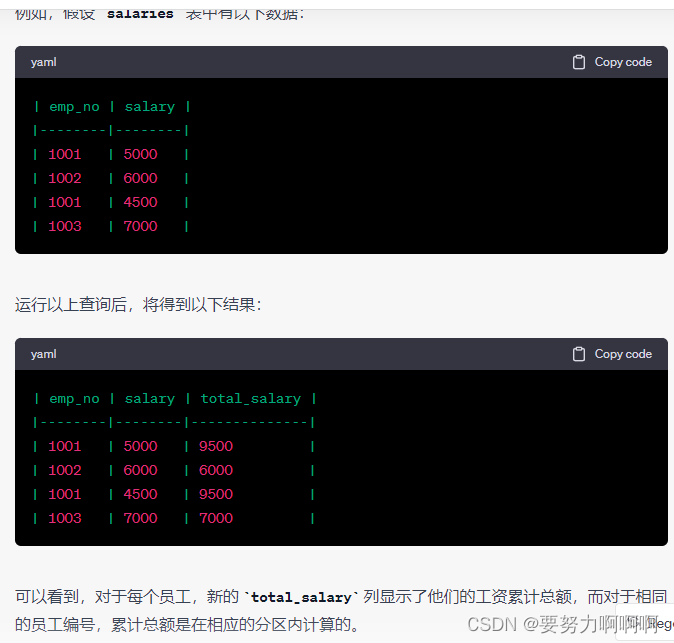
mysql中的窗口函数
MySQL中的窗口函数(Window Functions)是一种用于在查询结果集内执行计算的功能。窗口函数可以在查询中进行分析和聚合操作,而无需将查询结果分组。它们可以用于计算排名、行号、累积值等各种分析操作。窗口函数通常与OVER子句一起使用&#x…...

【双指针】经典数组双指针题LeetCode
文章目录 27. 移除元素 简单283. 移动零 简单🔥167. 两数之和 II - 输入有序数组 中等11. 盛最多水的容器 中等🔥15. 三数之和 中等(N数之和)中等🔥42. 接雨水 困难 🔥26. 删除有序数组中的重复项 简单5. 最…...

极智嘉x吉利汽车 x京东物流,引领汽车行业智慧物流新变革!
近日,中国领先的汽车制造商吉利汽车携手中国领先的技术驱动的供应链解决方案及物流服务商京东物流、全球仓储机器人引领者极智嘉(Geek),在西安吉利汽车制造基地RDC仓库率先落地SkyPick上存下拣解决方案,实现了全物流链精益化、智能化、一体化…...

RK3588平台开发系列讲解(AI 篇)RKNN C API 详细说明
文章目录 一、API 硬件平台支持说明二、API 函数介绍2.1、rknn_init2.2、rknn_destroy2.3、rknn_query2.4、rknn_inputs_set2.5、rknn_run2.6、rknn_outputs_get2.7、rknn_outputs_release沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇章主要讲解 RKNN C API 详细…...

【基础】Android Handler
一、博客参考 Handler机制详解【重点】:https://www.jianshu.com/p/b4d745c7ff7a Handler Thread工作线程操作UI范例【重点】:https://www.cnblogs.com/net168/p/4075126.html 二、内存泄漏的解决:静态内部类弱引用 关于 Handler…...
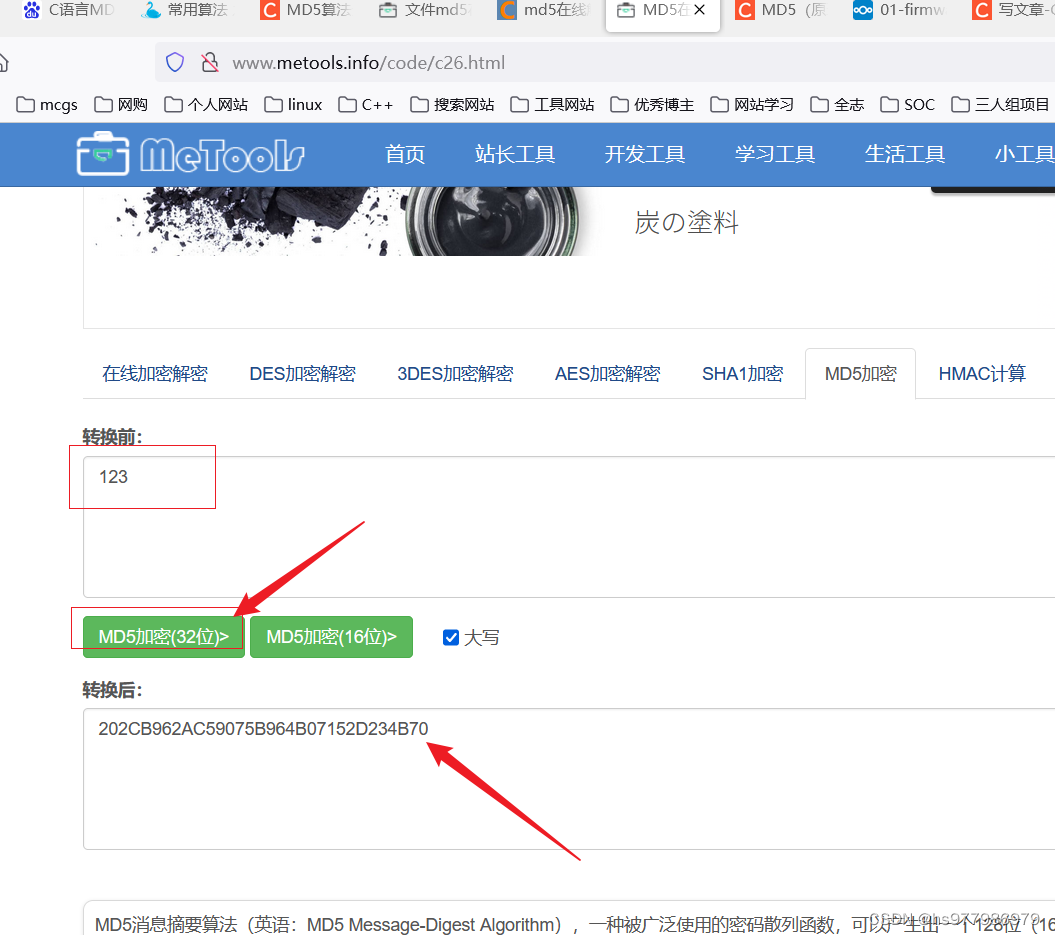
c语言实现MD5算法
MD5加密 文章目录 MD5加密MD5介绍应用场景代码分析 (基于qt5.14.2)测试记录 MD5介绍 1。 一种单向加密算法,即对明文加密,而不能通过密文得到明文。对原数据的任何改动,哪怕是1字节,得到的MD5值都有很大的区…...

Apache Doris 2.0.0 特性分析
1、存算分离 所谓存算分离是指查询外表时,使用一种专门做计算的BE节点,但对于存储在BE上的内部表,目前还不能做到存储分离。 doris可以查询外部表,包括: Hive、Iceberg、Hudi、Elasticsearch、JDBC、Paimon 早期版本中…...

如何做H5性能测试?
提起H5性能测试,可能许多同学有所耳闻,但是不知道该如何对H5做性能测试,或者不知道H5应该关注哪些性能指标。今天我们就来看下,希望阅读本文后,能够有所了解。 常用指标 1、H5性能相关参数介绍 白屏时间:…...
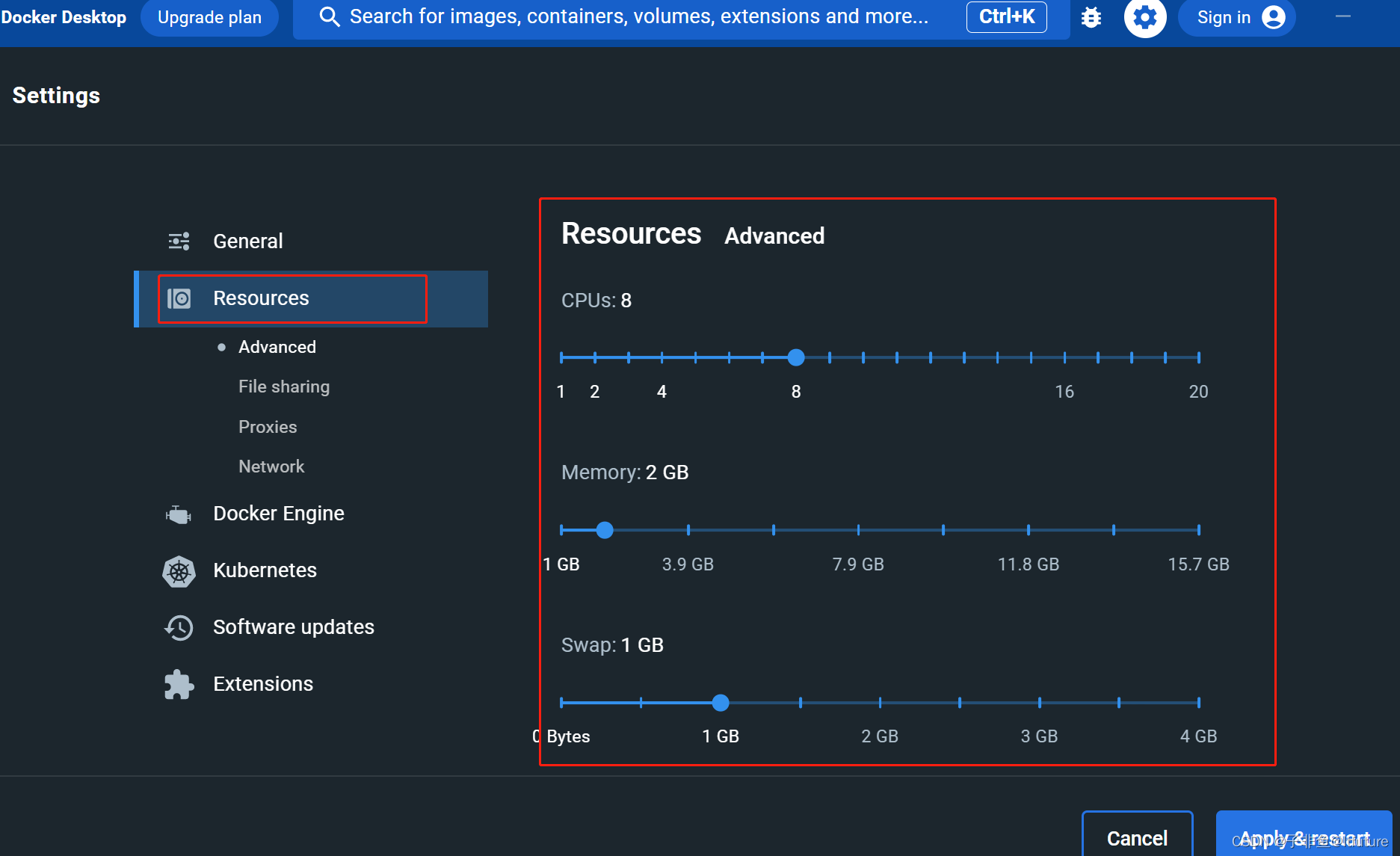
【Docker】Docker Desktop配置资源:cpu、内存等(windows环境下)
Docker Desktop配置资源:cpu、内存等(windows环境下) 一、WSL2 以及 hyper-v区别,二者安装docker desktop1.WSL2和hyper-v区别2.安装Docker Desktop 二、docker desktop限额配置,资源配置方法 Docker 是指容器化技术&a…...

8.2.tensorRT高级(3)封装系列-内存管理的封装,内存的复用
目录 前言1. 内存管理封装2. 补充知识总结 前言 杜老师推出的 tensorRT从零起步高性能部署 课程,之前有看过一遍,但是没有做笔记,很多东西也忘了。这次重新撸一遍,顺便记记笔记。 本次课程学习 tensorRT 高级-内存管理的封装&…...

Keepalived入门指南:实现故障转移和负载均衡
文章目录 一、简介1. Keepalived概述2. 高可用性和负载均衡的重要性 二、故障转移1. 什么是故障转移2. Keepalived的故障转移原理a) VRRP协议b) 虚拟路由器ID和优先级 3. 配置Keepalived实现故障转移a) 主备服务器的设置b) 监控网络接口c) 虚拟IP的配置d) 备份服务器接管流程 三…...

cuOSD(CUDA On-Screen Display Library)库的学习
目录 前言1. cuOSD1.1 Description1.2 Getting started1.3 For Python Interface1.4 Demo1.5 Performance Table 2. cuOSD案例2.1 环境配置2.2 simple案例2.3 segment案例2.4 segment2案例2.5 polyline案例2.6 comp案例2.7 perf案例 3. cuOSD浅析3.1 simple_draw函数 4. 补充知…...

c++函数指针基本用法
将函数像变量一样传递,实际上拿到的是函数的地址,由于函数类型的多样,可以使用auto关键字,可以使用 void(*function2)() ,不过它太繁琐,因此使用typedef 起个名字 typedef void(*HelloWorldFunction)(); 叫…...

Java创建对象的几种方式
在Java中,对象是程序中的一种基本元素,它通过类定义和创建。本篇教程旨在介绍Java中创建对象的几种方式,包括使用new关键字、反射、clone、反序列化等方式。 使用new关键字创建对象 在Java中,最常用的创建对象方式是使用new关键…...

Docker实战专栏简介
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
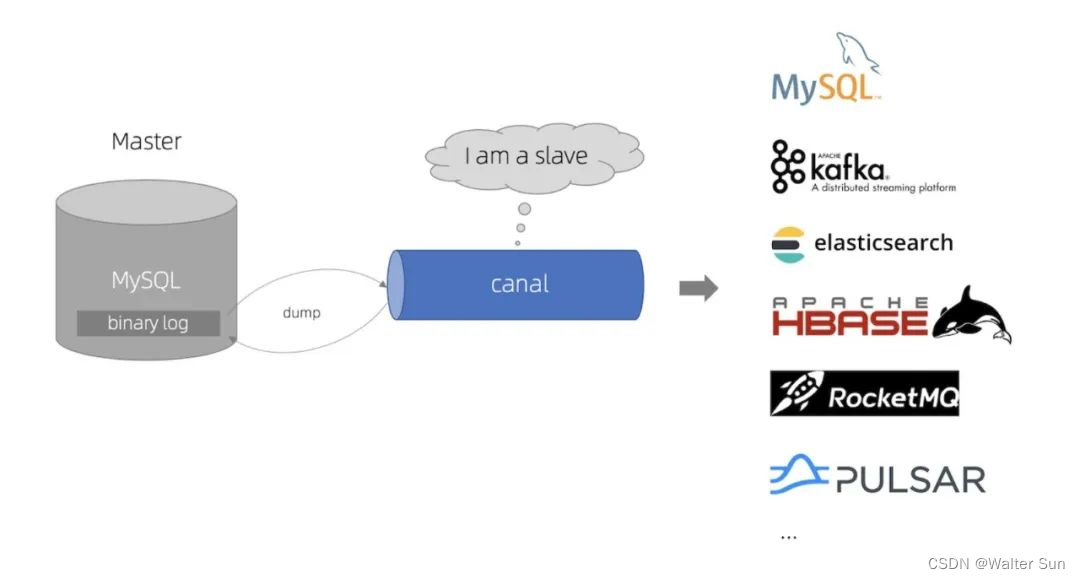
解放数据库,实时数据同步利器:Alibaba Canal
文章首发地址 Canal是一个开源的数据库增量订阅&消费组件,主要用于实时数据同步和数据订阅的场景,特别适用于构建分布式系统、数据仓库、缓存更新等应用。它支持MySQL、阿里云RDS等主流数据库,能够实时捕获数据库的增删改操作ÿ…...

机器学习基础之《分类算法(3)—模型选择与调优》
作用是如何选择出最好的K值 一、什么是交叉验证(cross validation) 1、定义 交叉验证:将拿到的训练数据,分为训练和验证集。以下图为例:将数据分成5份,其中一份作为验证集。然后经过5次(组)的测试&#x…...
Datawhale Django后端开发入门 TASK03 QuerySet和Instance、APIVIew
一、QuerySet QuerySet 是 Django 中的一个查询集合,它是由 Model.objects 方法返回的,并且可以用于生成数据库中所有满足一定条件的对象的列表。 QuerySet 在 Django 中表示从数据库中获取的对象集合,它是一个可迭代的、类似列表的对象集合。主要特点…...

Python 网页解析中级篇:深入理解BeautifulSoup库
在Python的网络爬虫中,BeautifulSoup库是一个重要的网页解析工具。在初级教程中,我们已经了解了BeautifulSoup库的基本使用方法。在本篇文章中,我们将深入学习BeautifulSoup库的进阶使用。 一、复杂的查找条件 在使用find和find_all方法查找…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...
