2023国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录
- 0 赛题思路
- 1 算法介绍
- 2 FP树表示法
- 3 构建FP树
- 4 实现代码
- 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 算法介绍
FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模式树算法,他与Apriori算法一样也是用来挖掘频繁项集的,不过不同的是,FP-Tree算法是Apriori算法的优化处理,他解决了Apriori算法在过程中会产生大量的候选集的问题,而FP-Tree算法则是发现频繁模式而不产生候选集。但是频繁模式挖掘出来后,产生关联规则的步骤还是和Apriori是一样的。
常见的挖掘频繁项集算法有两类,一类是Apriori算法,另一类是FP-growth。Apriori通过不断的构造候选集、筛选候选集挖掘出频繁项集,需要多次扫描原始数据,当原始数据较大时,磁盘I/O次数太多,效率比较低下。FPGrowth不同于Apriori的“试探”策略,算法只需扫描原始数据两遍,通过FP-tree数据结构对原始数据进行压缩,效率较高。
FP代表频繁模式(Frequent Pattern) ,算法主要分为两个步骤:FP-tree构建、挖掘频繁项集。
2 FP树表示法
FP树通过逐个读入事务,并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项,因此它们的路径可能部分重叠。路径相互重叠越多,使用FP树结构获得的压缩效果越好;如果FP树足够小,能够存放在内存中,就可以直接从这个内存中的结构提取频繁项集,而不必重复地扫描存放在硬盘上的数据。
一颗FP树如下图所示:
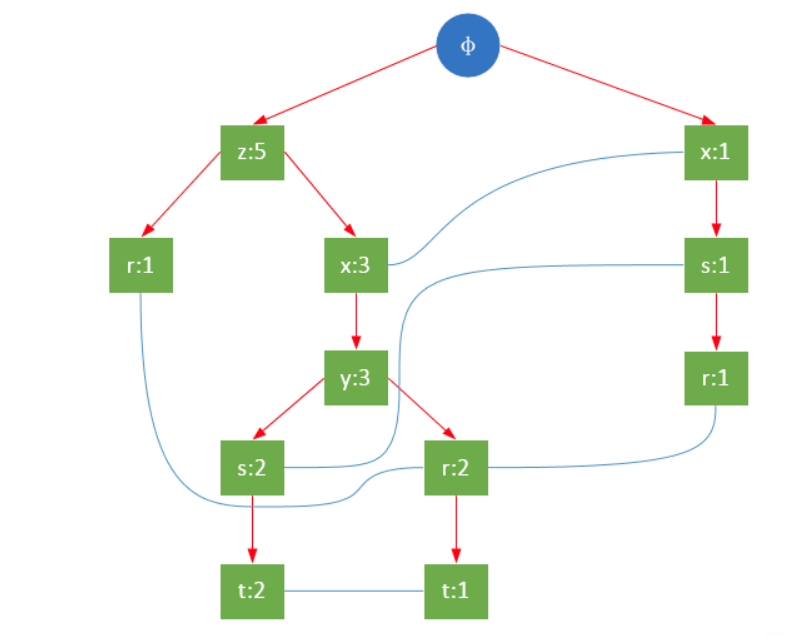
通常,FP树的大小比未压缩的数据小,因为数据的事务常常共享一些共同项,在最好的情况下,所有的事务都具有相同的项集,FP树只包含一条节点路径;当每个事务都具有唯一项集时,导致最坏情况发生,由于事务不包含任何共同项,FP树的大小实际上与原数据的大小一样。
FP树的根节点用φ表示,其余节点包括一个数据项和该数据项在本路径上的支持度;每条路径都是一条训练数据中满足最小支持度的数据项集;FP树还将所有相同项连接成链表,上图中用蓝色连线表示。
为了快速访问树中的相同项,还需要维护一个连接具有相同项的节点的指针列表(headTable),每个列表元素包括:数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针。
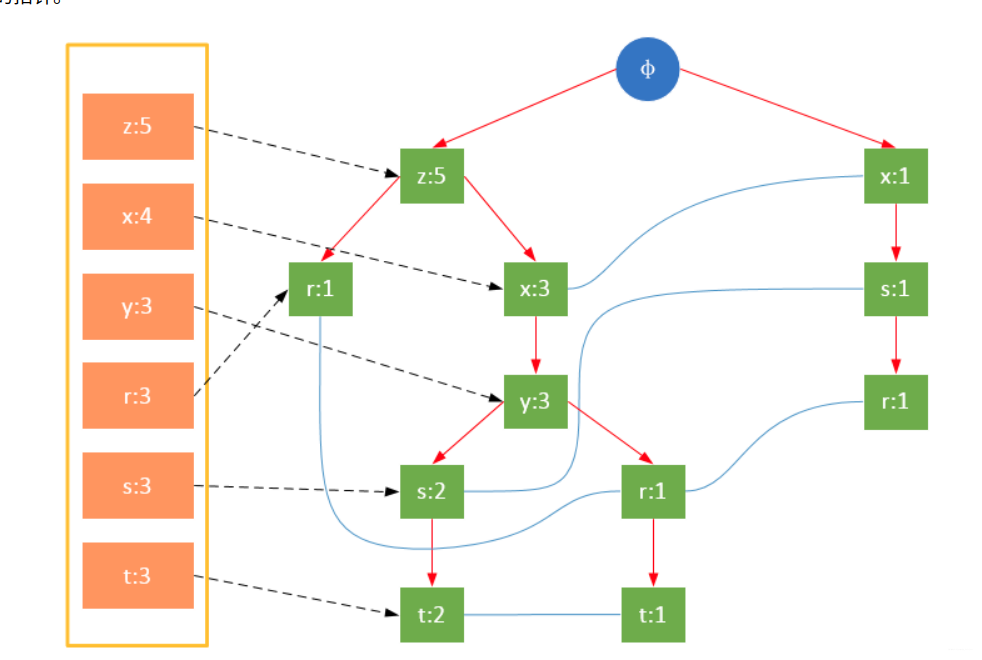
3 构建FP树
现在有如下数据:
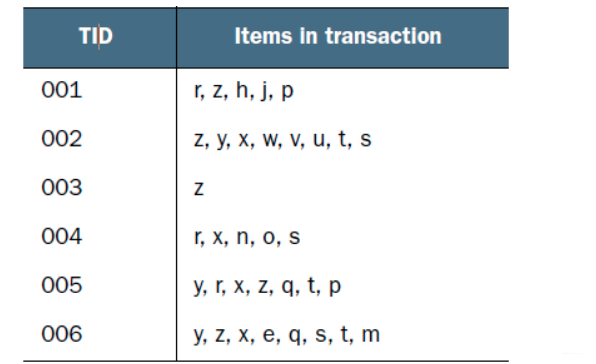
FP-growth算法需要对原始训练集扫描两遍以构建FP树。
第一次扫描,过滤掉所有不满足最小支持度的项;对于满足最小支持度的项,按照全局最小支持度排序,在此基础上,为了处理方便,也可以按照项的关键字再次排序。
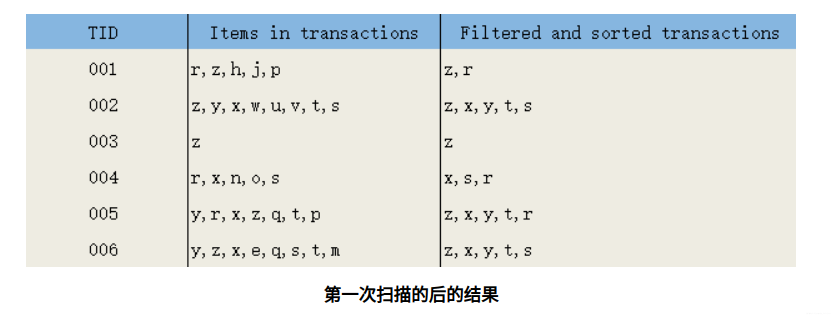
第二次扫描,构造FP树。
参与扫描的是过滤后的数据,如果某个数据项是第一次遇到,则创建该节点,并在headTable中添加一个指向该节点的指针;否则按路径找到该项对应的节点,修改节点信息。具体过程如下所示:
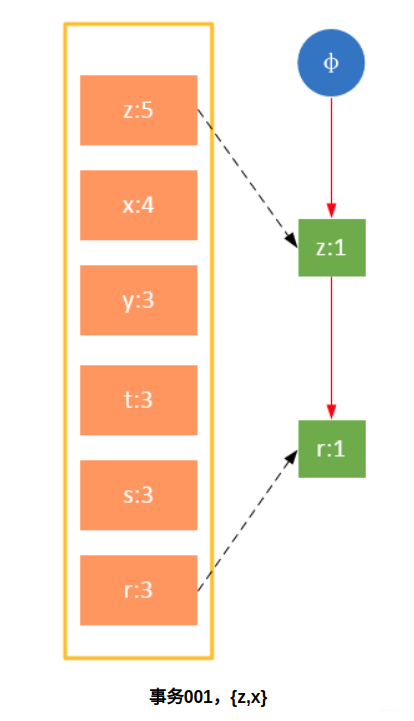
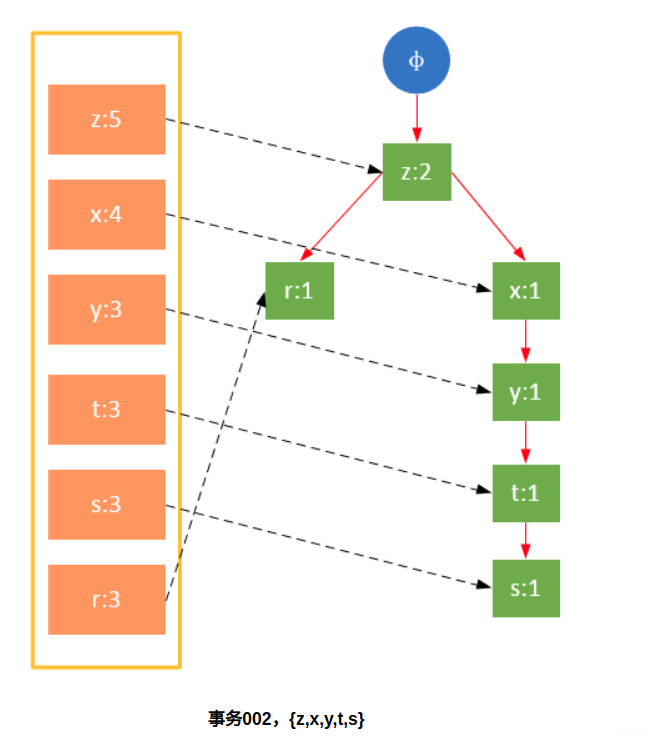
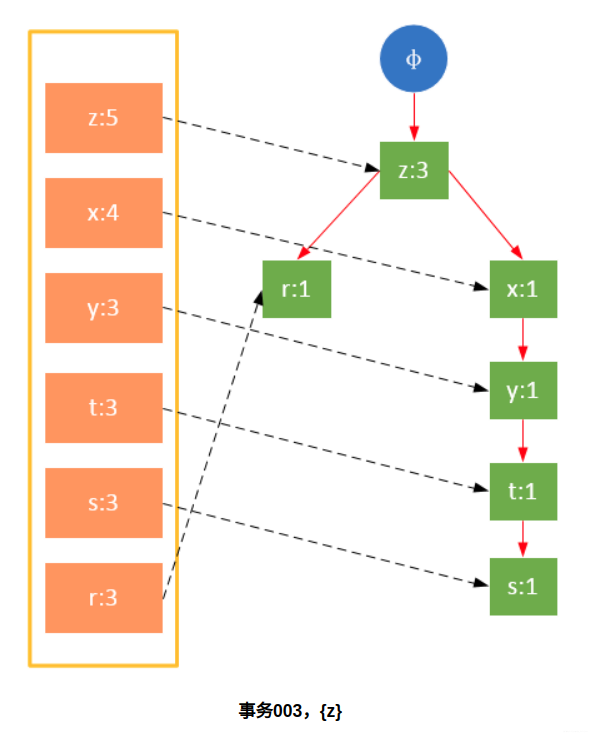
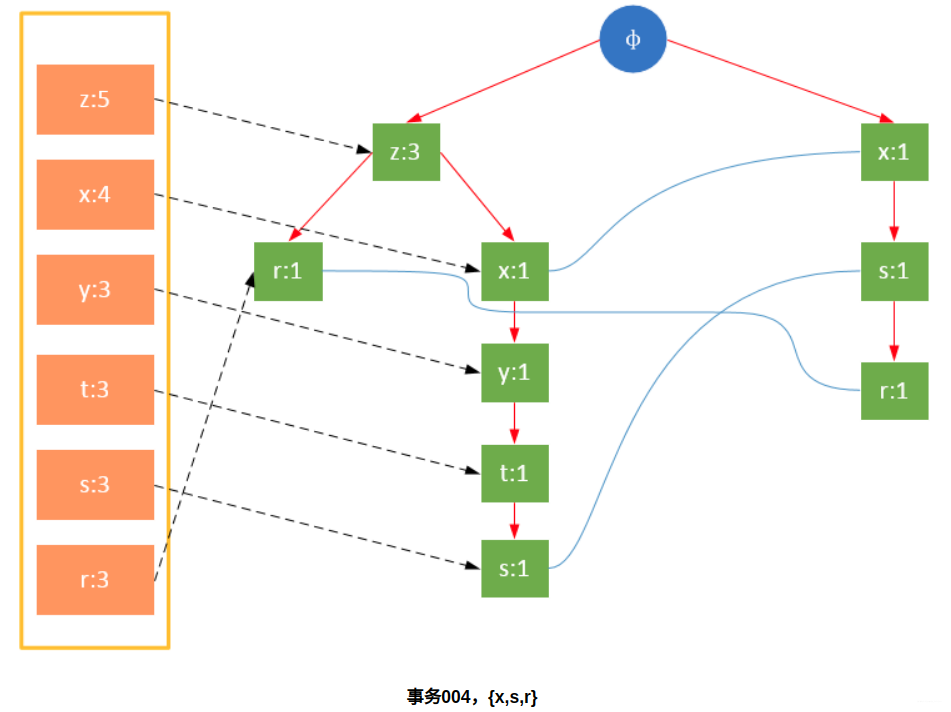
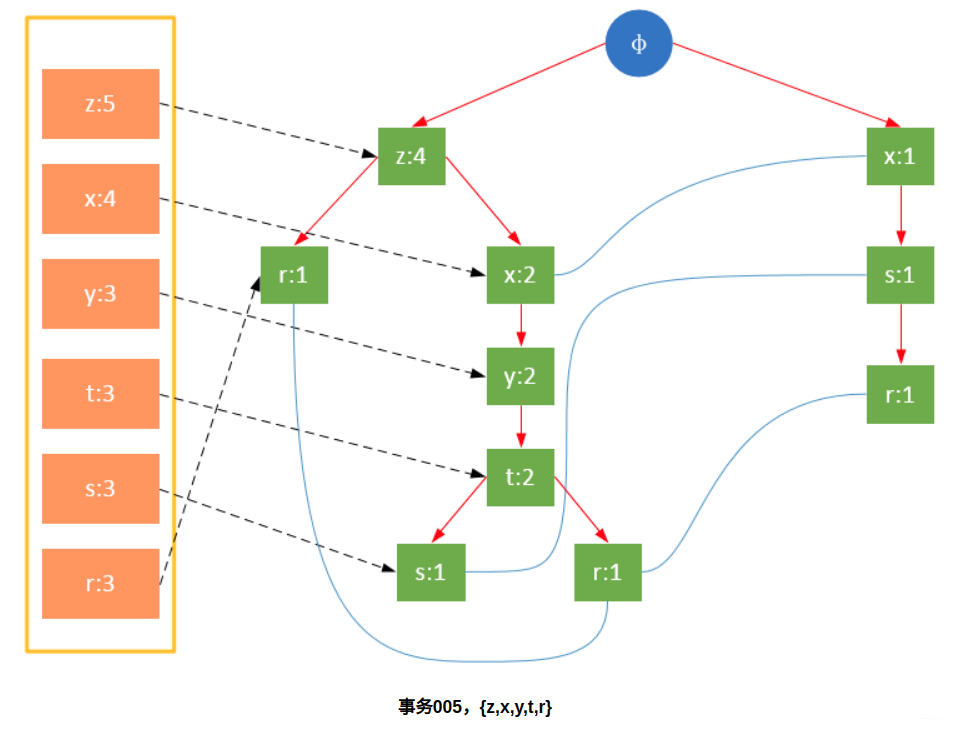
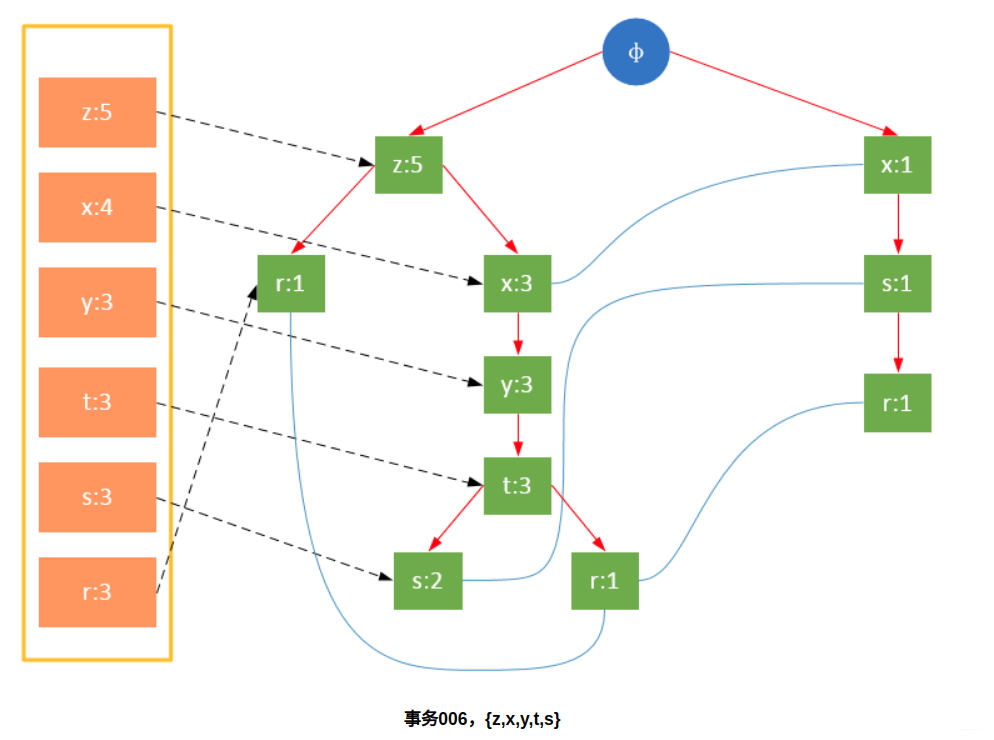
从上面可以看出,headTable并不是随着FPTree一起创建,而是在第一次扫描时就已经创建完毕,在创建FPTree时只需要将指针指向相应节点即可。从事务004开始,需要创建节点间的连接,使不同路径上的相同项连接成链表。
4 实现代码
def loadSimpDat():simpDat = [['r', 'z', 'h', 'j', 'p'],['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],['z'],['r', 'x', 'n', 'o', 's'],['y', 'r', 'x', 'z', 'q', 't', 'p'],['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]return simpDatdef createInitSet(dataSet):retDict = {}for trans in dataSet:fset = frozenset(trans)retDict.setdefault(fset, 0)retDict[fset] += 1return retDictclass treeNode:def __init__(self, nameValue, numOccur, parentNode):self.name = nameValueself.count = numOccurself.nodeLink = Noneself.parent = parentNodeself.children = {}def inc(self, numOccur):self.count += numOccurdef disp(self, ind=1):print(' ' * ind, self.name, ' ', self.count)for child in self.children.values():child.disp(ind + 1)def createTree(dataSet, minSup=1):headerTable = {}#此一次遍历数据集, 记录每个数据项的支持度for trans in dataSet:for item in trans:headerTable[item] = headerTable.get(item, 0) + 1#根据最小支持度过滤lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))for k in lessThanMinsup: del(headerTable[k])freqItemSet = set(headerTable.keys())#如果所有数据都不满足最小支持度,返回None, Noneif len(freqItemSet) == 0:return None, Nonefor k in headerTable:headerTable[k] = [headerTable[k], None]retTree = treeNode('φ', 1, None)#第二次遍历数据集,构建fp-treefor tranSet, count in dataSet.items():#根据最小支持度处理一条训练样本,key:样本中的一个样例,value:该样例的的全局支持度localD = {}for item in tranSet:if item in freqItemSet:localD[item] = headerTable[item][0]if len(localD) > 0:#根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] descorderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]updateTree(orderedItems, retTree, headerTable, count)return retTree, headerTabledef updateTree(items, inTree, headerTable, count):if items[0] in inTree.children: # check if orderedItems[0] in retTree.childreninTree.children[items[0]].inc(count) # incrament countelse: # add items[0] to inTree.childreninTree.children[items[0]] = treeNode(items[0], count, inTree)if headerTable[items[0]][1] == None: # update header tableheaderTable[items[0]][1] = inTree.children[items[0]]else:updateHeader(headerTable[items[0]][1], inTree.children[items[0]])if len(items) > 1: # call updateTree() with remaining ordered itemsupdateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode): # this version does not use recursionwhile (nodeToTest.nodeLink != None): # Do not use recursion to traverse a linked list!nodeToTest = nodeToTest.nodeLinknodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()
dictDat = createInitSet(simpDat)
myFPTree,myheader = createTree(dictDat, 3)
myFPTree.disp()
上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序,而是将排序放在了第二次扫描时,这可以简化代码的复杂度。
控制台信息:

建模资料
资料分享: 最强建模资料


相关文章:

2023国赛数学建模思路 - 案例:ID3-决策树分类算法
文章目录 0 赛题思路1 算法介绍2 FP树表示法3 构建FP树4 实现代码 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 算法介绍 FP-Tree算法全称是FrequentPattern Tree算法,就是频繁模…...
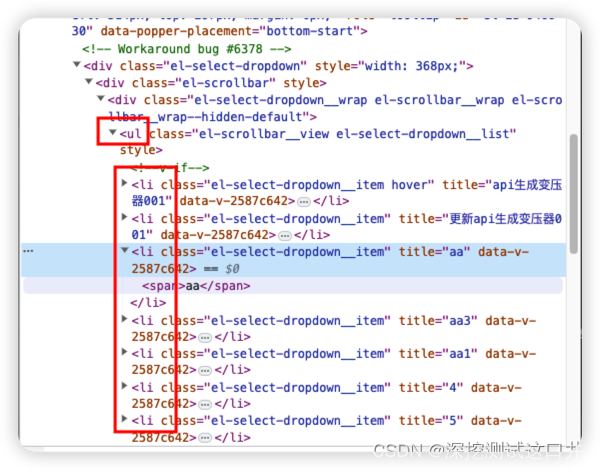
selenium 选定ul-li下拉选项中某个指定选项
场景:selenium的下拉选项是ul-li模式,选定某个指定的选项。 from selenium.webdriver.support.ui import WebDriverWait from selenium.webdriver.support import expected_conditions as EC # 显示等待def select_li(self, text, *ul_locator):"…...

回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现FA-SVM萤火虫算法优化支持向量机多输入单输出回归预测(多指标,多图)效果一览基本介绍…...

使用pytorch 的Transformer进行中英文翻译训练
下面是一个使用torch.nn.Transformer进行序列到序列(Sequence-to-Sequence)的机器翻译任务的示例代码,包括数据加载、模型搭建和训练过程。 import torch import torch.nn as nn from torch.nn import Transformer from torch.utils.data im…...

解决element的select组件创建新的选项可多选且opitions数据源中有数据的情况下,回车不能自动选中创建的问题
前言 最近开发项目使用element-plus库内的select组件,其中有提供一个创建新的选项的用法,但是发现一些小问题,在此记录 版本 “element-plus”: “^2.3.9”, “vue”: “^3.3.4”, 问题 1、在options数据源中无数据的时候,在输入框…...
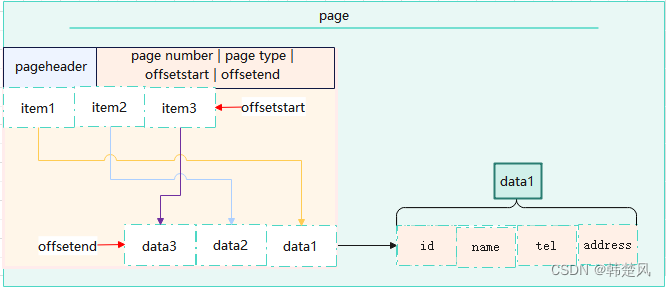
人工智能大模型加速数据库存储模型发展 行列混合存储下的破局
数据存储模型 专栏内容: postgresql内核源码分析手写数据库toadb并发编程toadb开源库 个人主页:我的主页 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 概述 在数据库的发展过程中,关…...
K8S用户管理体系介绍
1 K8S账户体系介绍 在k8s中,有两类用户,service account和user,我们可以通过创建role或clusterrole,再将账户和role或clusterrole进行绑定来给账号赋予权限,实现权限控制,两类账户的作用如下。 server acc…...
实现chatGPT 聊天样式
效果图 代码: <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Chat Example</title&g…...

day9 STM32 I2C总线通信
I2C总线简介 I2C总线介绍 I2C(Inter-Integrated Circuit)总线(也称IIC或I2C)是由PHILIPS公司开发的两线式串行总线,用于连接微控制器及其外围设备,是微电子通信控制领域广泛采用的一种总线标准。 它是同步通…...

终极Shell:Zsh(CentOS7 安装 zsh 及 配置 Oh my zsh)
CentOS7 安装 zsh 及 配置 Oh my zsh 我们在通过Shell操作linux终端时,配置、颜色区分、命令提示大都达不到我们预期的效果或者操作较为繁琐。 今天就来介绍一款终极一个及其好用的类Linux系统中的终端软件,江湖称之为马车中的跑车,跑车中的飞行车,史称『终极 Shell…...

Redis的数据持久化
前言 本文主要介绍Redis的三种持久化方式、AOF持久化策略等 什么是持久化 持久化是指将数据在内存中的状态保存到非易失性介质(如硬盘、固态硬盘等)上的过程。在计算机中,内存中的数据属于易失性数据,一旦断电或重启系统&#…...

CSS 选择器
前言 基础选择器 以下是几种常见的基础选择器。 标签选择器:通过HTML标签名称选择元素。 例如: p {color: red; } 上述样式规则将选择所有<p>标签 ,并将其文字颜色设置为红色。 类选择器:通过类名选择元素。使用类选择…...
)
上位机工作总结(2023.03-2023.08)
1.工作总结 不知不觉,已经从C#转为Qt开发快半年了。这半年内,也是学习了很多C相关的开发技能,同时自己的技术栈也是进一步丰富,以后跑路就更容易啦,哈哈!自己之前就有Winform和一些简单的Qt项目实践&#…...
APSIM模型参数优化 批量模拟丨气象数据准备、物候发育和光合生产、物质分配与产量模拟、土壤水分平衡算法、土壤碳氮平衡模块、农田管理模块等
随着数字农业和智慧农业的发展,基于过程的农业生产系统模型在模拟作物对气候变化的响应与适应、农田管理优化、作物品种和株型筛选、农田固碳和温室气体排放等领域扮演着越来越重要的作用。APSIM (Agricultural Production Systems sIMulator)模型是世界知名的作物生…...
Azure防火墙
文章目录 什么是Azure防火墙如何部署和配置创建虚拟网络创建虚拟机创建防火墙创建路由表,关联子网、路由配置防火墙策略配置应用程序规则配置网络规则配置 DNAT 规则 更改 Srv-Work 网络接口的主要和辅助 DNS 地址测试防火墙 什么是Azure防火墙 Azure防火墙是一种用…...
【LeetCode】剑指 Offer Ⅱ 第4章:链表(9道题) -- Java Version
题库链接:https://leetcode.cn/problem-list/e8X3pBZi/ 类型题目解决方案双指针剑指 Offer II 021. 删除链表的倒数第 N 个结点双指针 哨兵 ⭐剑指 Offer II 022. 链表中环的入口节点(环形链表)双指针:二次相遇 ⭐剑指 Offer I…...
Android SDK 上手指南|| 第三章 IDE:Android Studio速览
第三章 IDE:Android Studio速览 Android Studio是Google官方提供的IDE,它是基于IntelliJ IDEA开发而来,用来替代Eclipse。不过目前它还属于早期版本,目前的版本是0.4.2,每个3个月发布一个版本,最近的版本…...

Vue--》打造个性化医疗服务的医院预约系统(七)完结篇
今天开始使用 vue3 + ts 搭建一个医院预约系统的前台页面,因为文章会将项目的每一个地方代码的书写都会讲解到,所以本项目会分成好几篇文章进行讲解,我会在最后一篇文章中会将项目代码开源到我的GithHub上,大家可以自行去进行下载运行,希望本文章对有帮助的朋友们能多多关…...
点亮一颗LED灯
TOC LED0 RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOB,ENABLE);//使能APB2的外设时钟GPIO_InitTypeDef GPIO_Initstructure;GPIO_Initstructure.GPIO_Mode GPIO_Mode_Out_PP;//通用推挽输出GPIO_Initstructure.GPIO_Pin GPIO_Pin_5;GPIO_Initstructure.GPIO_Speed GPIO_S…...
SSH远程直连--------------Docker容器
文章目录 1. 下载docker镜像2. 安装ssh服务3. 本地局域网测试4. 安装cpolar5. 配置公网访问地址6. SSH公网远程连接测试7.固定连接公网地址8. SSH固定地址连接测试 在某些特殊需求下,我们想ssh直接远程连接docker 容器,下面我们介绍结合cpolar工具实现ssh远程直接连接docker容器…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
