洛谷P8601[蓝桥杯][2013年第四届真题]剪格子
题目描述
如图 11 所示,3×3 的格子中填写了一些整数。

我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 60。
本题的要求就是请你编程判定:对给定的 m×n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0。
输入格式
程序先读入两个整数m,n 用空格分割 (m,n<10)表示表格的宽度和高度。
接下来是 n 行,每行 m 个正整数,用空格分开。每个整数不大于10000。
输出格式
程序输出:在所有解中,包含左上角的分割区可能包含的最小的格子数目。
输入输出样例
输入
3 3
10 1 52
20 30 1
1 2 3
输出
3
输入
4 3
1 1 1 1
1 30 80 2
1 1 1 100
输出
10
说明/提示
第二个用例中:

时限 5 秒, 64M。蓝桥杯 2013 年第四届省赛
思路:利用搜索遍历每一种解决方案,把每种解决方案中格子的个数记录下来,然后输出最少格子数
#include<iostream>
using namespace std;
int g[11][11];
int vis[11][11];
int n, m, num[10010], sum, s, k;
int xx[] = { 1,0,-1,0 };
int yy[] = { 0,1,0,-1 };
void dfs(int x, int y)
{if (s == sum / 2){for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (vis[i][j] == 1) num[k]++;}}k++;return;}for (int i = 0; i < 4; i++){int dx = x + xx[i];int dy = y + yy[i];if (dx>=1 && dx<=n && dy>=1 && dy<=m && vis[dx][dy]==0 ){vis[dx][dy] = 1;s += g[dx][dy];dfs(dx, dy);s -= g[dx][dy]; //回溯vis[dx][dy] = 0;}}
}
int main()
{cin >> m >> n;int i, j;for (i = 1; i <= n; i++){for (j = 1; j <= m; j++){cin >> g[i][j];sum += g[i][j];}}vis[1][1] = 1;s += g[1][1];dfs(1, 1);int minn = num[0];for (i = 0; i < k; i++){minn = min(minn, num[i]);}cout << minn << endl;return 0;
}这串代码在洛谷中只能跑过3个测试案例,暂时还没有找到更好的解决方法,呜呜~~

相关文章:

洛谷P8601[蓝桥杯][2013年第四届真题]剪格子
题目描述如图 11 所示,33 的格子中填写了一些整数。我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 60。本题的要求就是请你编程判定:对给定的 mn 的格子中的整数,是否可以分割为两个部分,使…...

配置alias实现快速生成.gitignore文件
git工具:版本控制开发工具。 cscope工具:用于浏览C源码的工具,类似于ctags。在代码根目录下执行cscope -Rbq,然后产生三个索引文件(cscope.out、cscope.in.out和cscope.po.out三个文件)。 在Linux下使用vi…...

MySQL数据库调优————GROUP BY及DISTINCT优化
GROUP BY 三种处理GROUP BY的方式 松散索引扫描(Loose Index Scan)紧凑索引扫描(Tight Index Scan)临时表(Temporary table) 三种方式的性能一次递减 松散索引扫描 无需扫描满足条件的所有索引键即可返…...

LRU缓存算法
双向链表哈希表(非线程安全) https://leetcode.cn/problems/lru-cache/solutions/259678/lruhuan-cun-ji-zhi-by-leetcode-solution/ /*** LRU算法: 哈希表双向链表实现* 1. 双向链表按照被使用的顺序来存储, 靠近头部的节点是最近使用的, 靠近尾部的节…...

@Configuration注解
Configuration注解介绍 Configuration注解,用于标注一个类是一个spring的配置类(同时,也是一个bean),配置类中可以使用ComponentScan、Import、ImportResource 和 Bean等注解的方式定义beanDefinition。 Target(Elem…...

基于springboot+vue的食疗系统
基于springbootvue的食疗系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍&…...
sklearn学习-朴素贝叶斯
文章目录一、概述1、真正的概率分类器2、sklearn中的朴素贝叶斯二、不同分布下的贝叶斯1、高斯朴素贝叶斯GaussianNB2、探索贝叶斯:高斯朴素贝叶斯擅长的数据集3、探索贝叶斯:高斯朴素贝叶斯的拟合效果与运算速度总结一、概述 1、真正的概率分类器 算法…...

分享112个HTML艺术时尚模板,总有一款适合您
分享112个HTML艺术时尚模板,总有一款适合您 112个HTML艺术时尚模板下载链接:https://pan.baidu.com/s/1D3-mfPOud-f3vy9yLl-bmw?pwdfph2 提取码:fph2 Python采集代码下载链接:采集代码.zip - 蓝奏云 时尚平面模特网站模板 潮…...

用GDB远程调试运行于QEMU的程序
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 测试环境 本文使用 Ubuntu 16.04.4 LTS QEMU 环境进行调试。 3. 用 GDB 调试 QEMU 内程序 3.1 编写用来调试的程序 我们用 ARM32 来进行调试…...
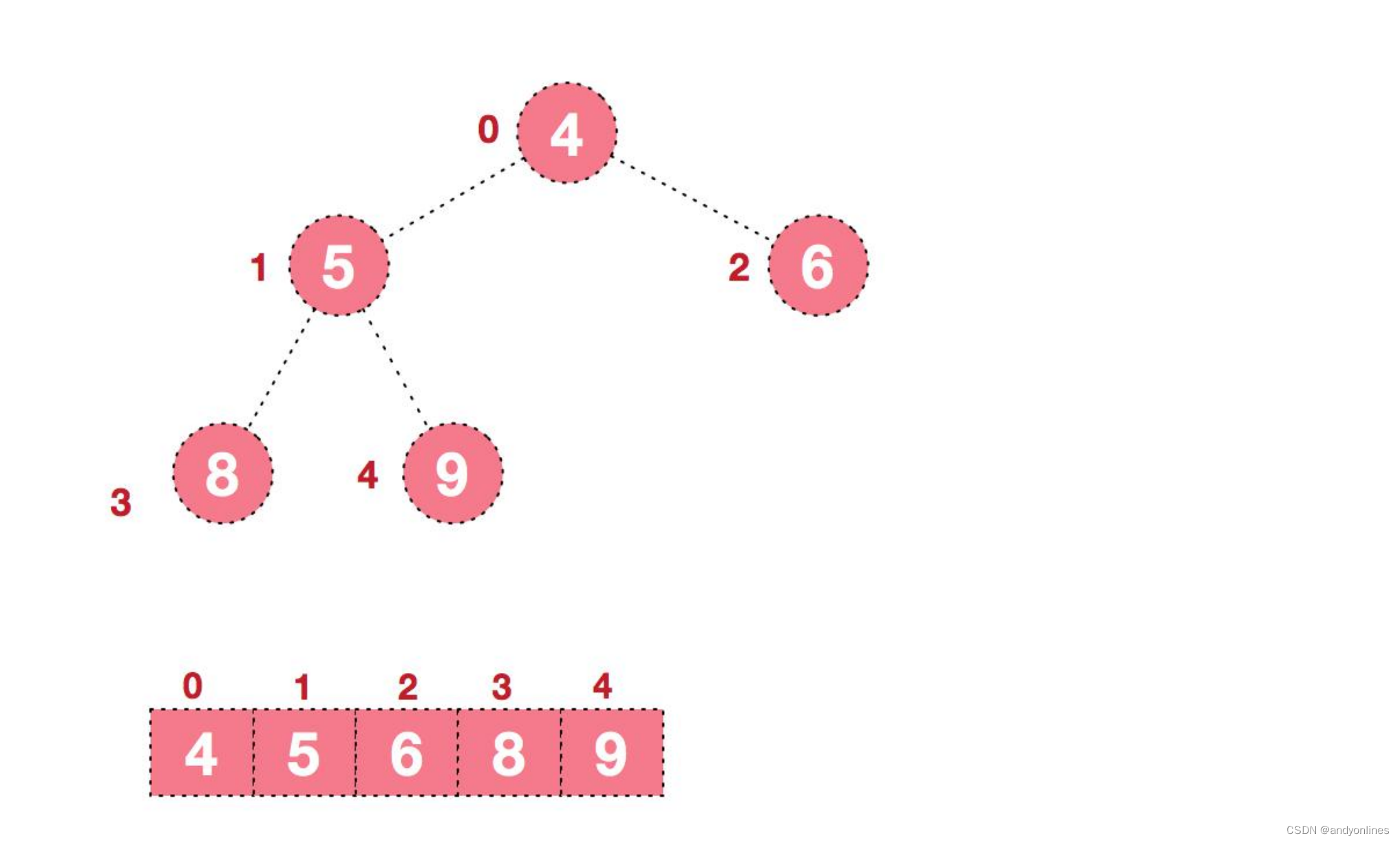
20 堆排序
文章目录1 堆排序的概念2 堆排序基本思想3 堆排序步骤图解说明4 堆排序的代码实现1 堆排序的概念 1) 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为 O(nlogn)…...
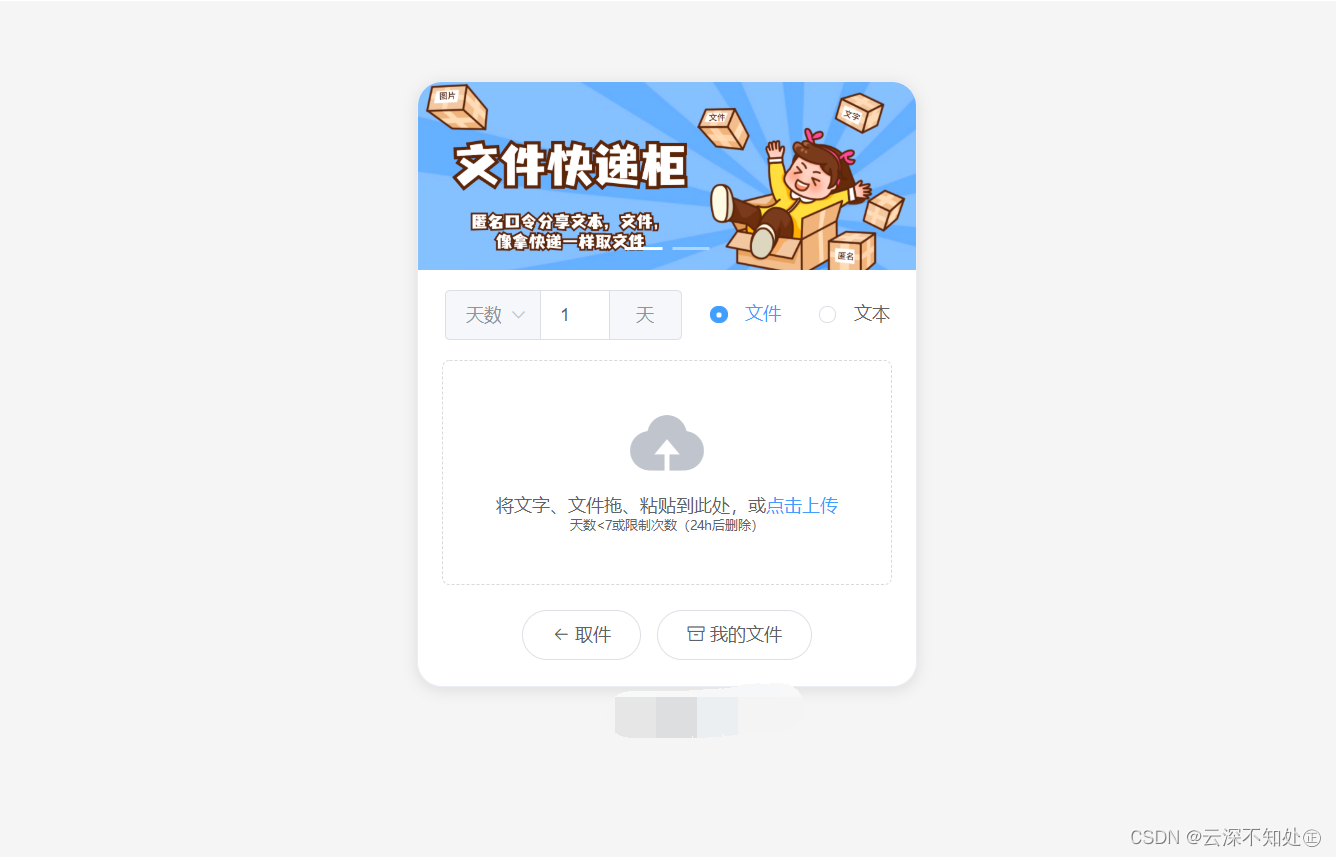
2023最新文件快递柜系统网站源码 | 匿名口令分享 | 临时文件分享
内容目录一、详细介绍二、效果展示1.部分代码2.效果图展示三、学习资料下载一、详细介绍 2023最新文件快递柜系统网站源码 | 匿名口令分享 | 临时文件分享 很多时候,我们都想将一些文件或文本传送给别人,或者跨端传递一些信息,但是我们又不…...
)
分片策略(二)
分片策略 基本概念 分片键 用于分片的字段,是将数据库或表拆分的字段,比如,我可以使用user_id作为分片键将用户数据分到不同的表中,这里的user_id就是分片键,除了这种单字段分片,ShardingSphere还支持多…...
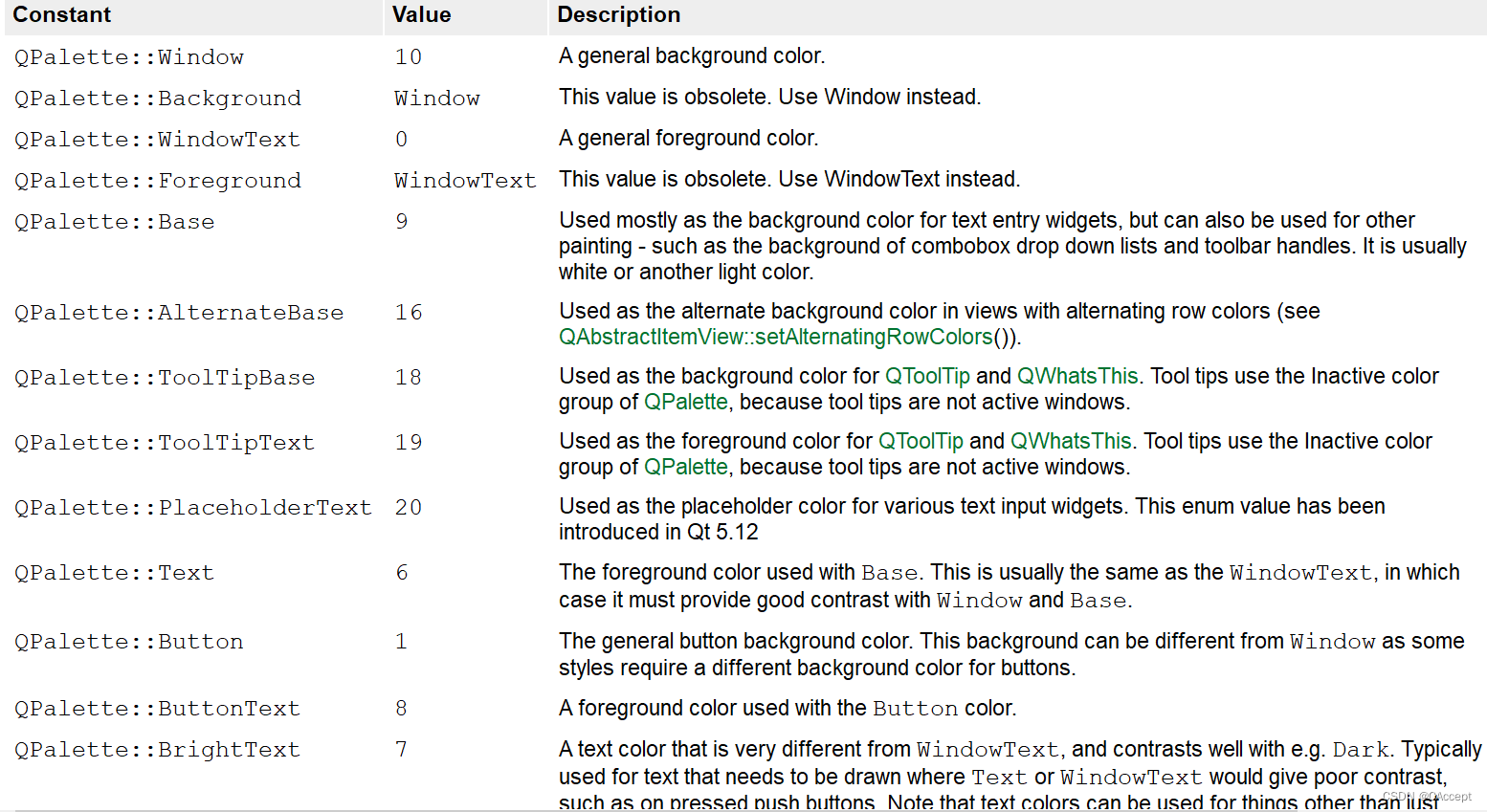
Qt之调色板类QPalette的使用
文章目录QPalette调色板类前言代码知识点讲解QPalette调色板类 前言 Qt提供的调色板类QPalette专门用于管理部件的外观显示,相当于部件或对话框的调色板,管理他们所有的颜色信息。每个部件都包含一个QPalette对象,在显示时,按照…...
Kotlin 32. Kotlin 多语言支持
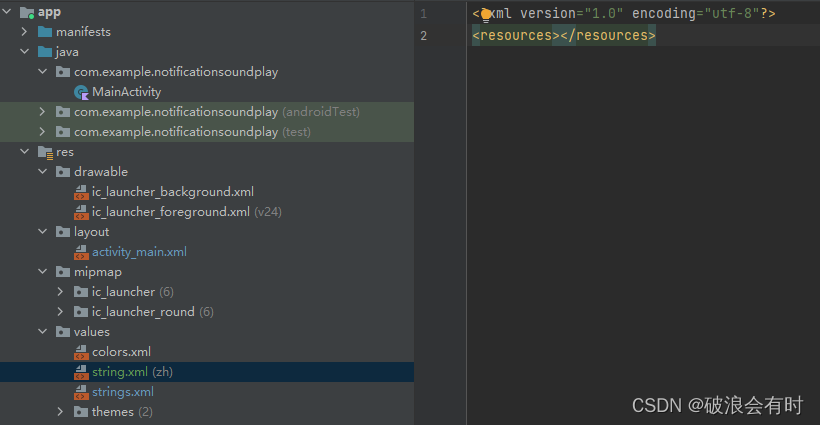
Kotlin 多语言支持 对于 Kotlin 来说,当我们新建一个项目时,会默认在 values/ 文件夹下,生成一个 strings.xml 文件。比如说, <resources><string name"app_name">exampleNewProject</string> <…...
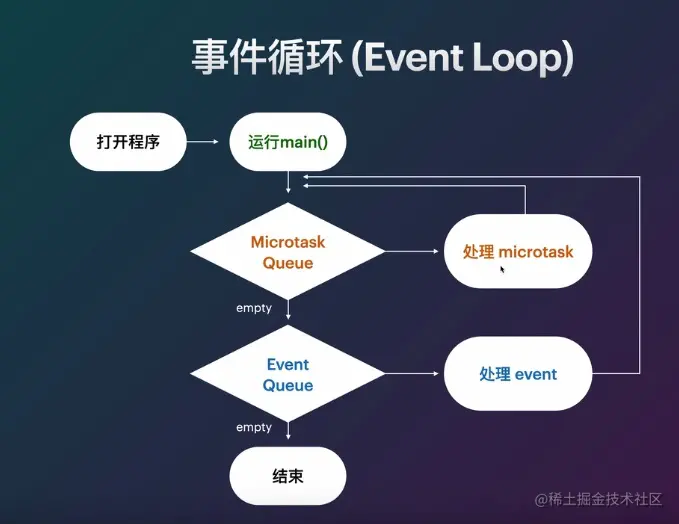
【Flutter入门到进阶】Dart进阶篇---DartVM单线程设计原理
1 虚拟机的指令执行设计 1.1 虚拟机的分类 基于栈的虚拟机,比如JVM虚拟机 基于寄存器的虚拟机,比如Dalvik虚拟机 1.2 虚拟机的概念 首先问一个基本的问题,作为一个虚拟机,它最基本的要实现哪些功能? 他应该能够模拟…...
的交集)
Dem和NvM(NVRAM Manager)的交集
NVRAM(NvM)提供了在NVRAM中存储数据Block的机制。 NVRAM Block(最大大小取决于配置)被分配给Dem,并由Dem实现事件状态信息和相关数据的永久存储(例如通电复位)。 ECU 状态管理器(Ec…...

AI神经网络CNN/RNN/DNN/SNN的区别对比
@版权声明: 本文由 ChatGpt 创作; BiliBili: https://www.bilibili.com/video/BV17D4y1P7pM/?share_source=copy_web&vd_source=6d217e0ff6387a749dc570aba51d36fd 引言 随着人工智能技术的发展,神经网络作为人工智能的核心技术之一,被广泛应用于图像识别、语音识别、…...

【JavaWeb】一文学会JPA
✅✅作者主页:🔗孙不坚1208的博客 🔥🔥精选专栏:🔗JavaWeb从入门到精通(持续更新中) 📋📋 本文摘要:本篇文章主要介绍JPA的概念、注解实现ORM规范…...
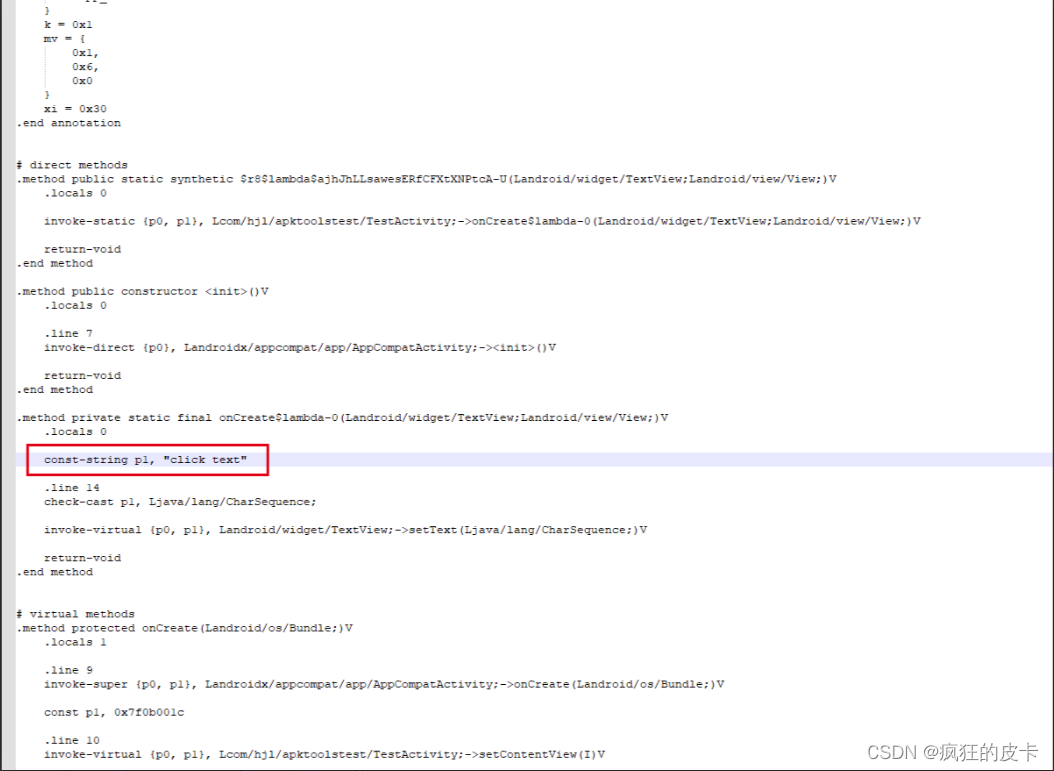
【安卓逆向】APK修改与反编译回编译
【安卓逆向】反编译修改APK回编译使用工具流程步骤Apktool相关安装与使用常用命令备查APK签名命令备查实战练习反编译查看修改的地方使用Apktool反编译得到产物文件夹并进行修改回编APK实用场景在日常开发我们可能需要替换某些资源或者修改某些代码,但是我们没有源码…...

【计组笔记04】计算机组成原理之多模块存储器、Cache高速缓存存储器、Cache地址映射
这篇文章,主要介绍计算机组成原理之多模块存储器、Cache高速缓存存储器、Cache地址映射。 目录 一、双口RAM和多模块存储器 1.1、存取周期 1.2、双口RAM 1.3、多模块存储器...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
