clion软件ide的安装和环境配置@ubuntu
1.官网:
Download CLion
2.安装Clion
直接在官网下载并安装即可,过程很简单
https://www.jetbrains.com/clion/
https://www.jetbrains.com/clion/download/#section=linux
3.激活码
4.配置Clion
安装gcc、g++、make
Ubuntu中用到的编译工具是gcc©,g++(C++),make(连接)。因此只需安装对应的工具包即可。Ubuntu下使用命令安装这些包:
(1)安装gcc
sudo apt install gcc
(2)安装g++
sudo apt install g++
(3)安装make
sudo apt install make
5.替换jbr文件夹
jetbrains全家桶在Ubuntu中使用会出现输入法不跟随的问题,需要将源文件中的jbr文件夹替换来解决
https://github.com/JetBrains/JetBrainsRuntime/releases/tag
6.链接:
Ubuntu下安装Clion_ubuntu安装clion_阿栋阿栋的博客-CSDN博客
Ubuntu安装搭建Clion环境
CLion安装与配置教程_clion安装和配置_小白学CS的博客-CSDN博客
ubuntu下安装和配置Clion
相关文章:

clion软件ide的安装和环境配置@ubuntu
1.官网: Download CLion 2.安装Clion 直接在官网下载并安装即可,过程很简单 https://www.jetbrains.com/clion/ https://www.jetbrains.com/clion/download/#sectionlinux 3.激活码 4.配置Clion 安装gcc、g、make Ubuntu中用到的编译工具是gcc©…...
Cpp学习——类与对象3
目录 一,初始化列表 1.初始化列表的使用 2.初始化列表的特点 3.必须要使用初始化列表的场景 二,单参数构造函数的隐式类型转换 1.内置类型的隐式类型转换 2. 自定义类型的隐式类型转换 3.多参数构造函数的隐式类型转换 4.当你不想要发生隐式类型转换…...

回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图&a…...
)
ahooks.js:一款强大的React Hooks库及其API使用教程(四)
一、ahooks.js简介二、ahooks.js安装三、继续ahooks.js API的介绍与使用教程51. useResetState52. useUpdateLayoutEffect53. useDeepCompareLayoutEffect54. useRafInterval55. useRafTimeout56. useTimeout57. useLockFn58. useDocumentVisibility59. useDrop60. useDrag 一、…...

FOSSASIA Summit 2023 - 开源亚洲行
作者 Ted 致歉:本来这篇博客早就该发出,但是由于前几个月频繁差旅导致精神不佳,再加上后续我又参加了 Linux 基金会 7/27 在瑞士日内瓦举办的 Open Source Congress,以及 7/29-30 台北的 COSCUP23,干脆三篇连发&#x…...
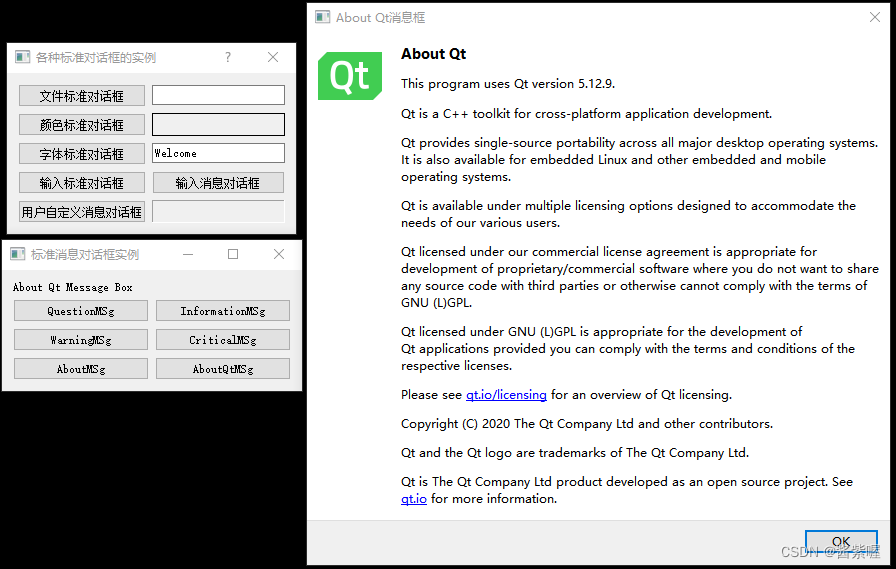
QT 基本对话框
包括: 1.标准文件对话框 dialog.h #ifndef DIALOG_H #define DIALOG_H#include <QDialog> #include <QTextCodec> #include <QLabel> #include <QLineEdit> #include <QPushButton> #include <QGridLayout> #include <QFr…...

8th参考文献:[8]许少辉.乡村振兴战略下传统村落文化旅游设计[M]北京:中国建筑出版传媒,2022.
8th参考文献:[8]许少辉.乡村振兴战略下传统村落文化旅游设计[M]北京:中国建筑出版传媒,2022&…...
Azure静态网站托管
什么是静态网站托管 Azure Blob的静态网站托管是一项功能,它允许开发人员在Azure Blob存储中托管和发布静态网站。通过这个功能,您可以轻松地将静态网页、图像、视频和其他网站资源存储在Azure Blob中,并直接通过提供的URL访问这些资源。 官…...
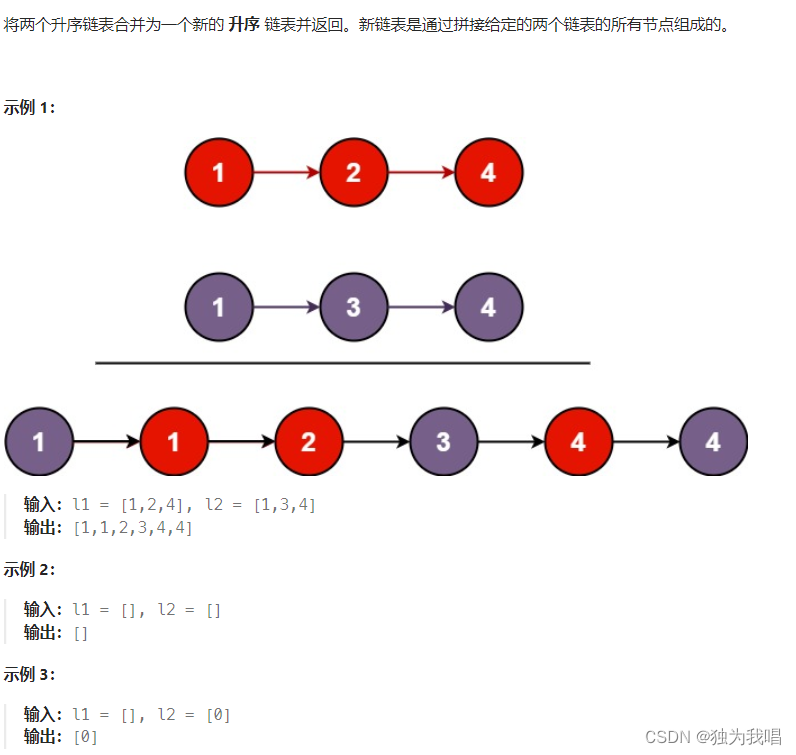
LeetCode 热题 100(五):54. 螺旋矩阵、234. 回文链表、21. 合并两个有序链表
题目一: 54. 螺旋矩阵https://leetcode.cn/problems/spiral-matrix/ 题目要求: 思路:一定要先找好边界。如下图 ,上边界是1234,右边界是8、12,下边界是9、10、11,左边界是5,所以可…...

常用消息中间件介绍
RocketMQ 阿里开源,阿里参照kafka设计的,Java实现 能够保证严格的消息顺序 提供针对消息的过滤功能 提供丰富的消息拉取模式 高效的订阅者水平扩展能力 实时的消息订阅机制 亿级消息堆积能力 RabbitMQ Erlang实现,非常重量级,更适…...
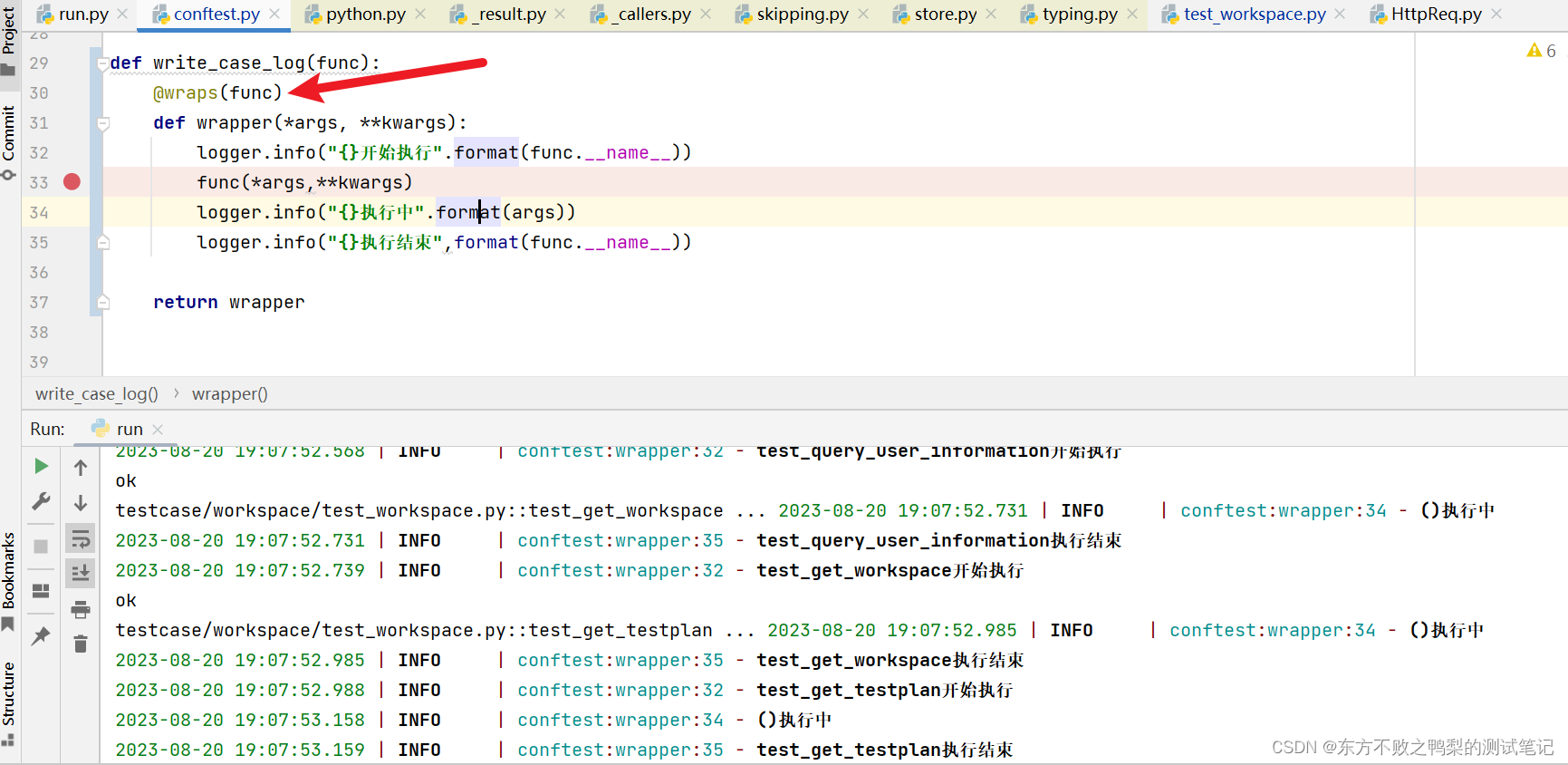
装饰器读取不到被装饰函数的参数-已解决
def write_case_log(func):def wrapper(*args, **kwargs):logger.info("{}开始执行".format(func.__name__))func(*args,**kwargs)logger.info("{}执行中".format(args))logger.info("{}执行结束",format(func.__name__))return wrapper被装饰函…...

python爬虫爬取中关村在线电脑以及参数数据
一. 内容简介 python爬虫爬取中关村在线电脑以及参数数据 二. 软件环境 2.1vsCode 2.2Anaconda version: conda 22.9.0 三.主要流程 3.1 代码 解析都在代码里面 # 接口分析 # 原始接口,后面几个数字就是占位的,每个位置代表着不同的标签 # http…...

chatGPT-对话爱因斯坦
引言 阿尔伯特爱因斯坦( 1879年 3 月 14 日 – 1955 年 4 月 18 日)是一位出生于德国的理论物理学家,被广泛认为成为有史以来最伟大、最有影响力的科学家之一。他以发展相对论而闻名,他还对量子力学做出了重要贡献,因…...

嵌入式软件开发中的数据类型转换
在嵌入式软件开发时,数据的显示必不可少,那么必定会涉及到数据类型转换。将不同类型的数据在编程中进行转换,以便满足不同的需求。 插入一个知识点: 在C语言中,字符串是由字符组成的字符数组,以null终止符…...
)
The Go Blog 01:反射的法则(译文)
反思的法则 罗伯-派克 2011 年 9 月 6 日 引言 计算机中的反射是指程序检查自身结构的能力,尤其是通过类型检查自身结构的能力;它是元编程的一种形式。它也是造成混乱的一个重要原因。 在本文中,我们试图通过解释 Go 中的反射是如何工作的…...

Visual Studio Code前端开发插件推荐
引言 Visual Studio Code(简称VS Code)是一款轻量级且强大的开源代码编辑器,广受前端开发者的喜爱。其丰富的插件生态系统为前端开发提供了许多便利和增强功能的插件。本篇博客将向大家推荐一些在前端开发中常用且优秀的插件,并提…...

jps(JVM Process Status Tool):虚拟机进程状况工具
jps(JVM Process Status Tool):虚拟机进程状况工具 列出正在运行的虚拟机进程,并显示虚拟机执行主类名称(Main Class,main()函数所在的类)以及这些进程的本地虚拟机唯一ID(LVMID&am…...

初阶c语言:实战项目三子棋
前言 大家已经和博主学习有一段时间了,今天讲一个有趣的实战项目——三子棋 目录 前言 制作菜单 构建游戏选择框架 实现游戏功能 模块化编程 初始化棋盘 打印棋盘 玩家下棋 电脑下棋 时间戳:推荐一篇 C语言生成随机数的方法_c语言随机数_杯浅…...
计网第三章(数据链路层)(三)
一、点对点协议PPP 在第一篇里有提到数据链路层的信道分为两种:点对点信道和广播信道。 PPP协议就属于点对点信道上的协议。 如果对前面数据链路层的三个基本问题了解的比较透彻,那么这一块很多东西都很好理解。 从考试的角度来讲,PPP协议…...
)
蓝桥杯每日N题 (砝码称重)
大家好 我是寸铁 希望这篇题解对你有用,麻烦动动手指点个赞或关注,感谢您的关注 不清楚蓝桥杯考什么的点点下方👇 考点秘籍 想背纯享模版的伙伴们点点下方👇 蓝桥杯省一你一定不能错过的模板大全(第一期) 蓝桥杯省一你一定不…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
