剑指 Offer 65. 不用加减乘除做加法
摘要
剑指 Offer 65. 不用加减乘除做加法
一、位运算
有符号整数通常用补码来表示和存储,补码具有如下特征:
- 正整数的补码与原码相同;负整数的补码为其原码除符号位外的所有位取反后加 11。
- 可以将减法运算转化为补码的加法运算来实现。
- 符号位与数值位可以一起参与运算。
思路和算法:虽然题目只要求了不能使用运算符+、-、*和/,但是原则上来说也不宜使用类似的运算符+=、-=、*=和/=,以及sum等方法。于是,我们使用位运算来处理这个问题。首先,考虑两个二进制位相加的四种情况如下:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 (进位)
可以发现,对于整数a和b:
- 在不考虑进位的情况下,其无进位加法结果为 a⊕b。
- 而所有需要进位的位为a&b,进位后的进位结果为 (a & b) << 1。
于是,我们可以将整数a和 b的和,拆分为a和b的无进位加法结果与进位结果的和。因为每一次拆分都可以让需要进位的最低位至少左移一位,又因为a和 b可以取到负数,所以我们最多需要 log(max_int)次拆分即可完成运算。因为有符号整数用补码来表示,所以以上算法也可以推广到0 和负数。
class Solution {public int add(int a, int b) {while (b != 0) {int carry = (a & b) << 1;a = a ^ b;b = carry;}return a;}
}复杂度分析
- 时间复杂度:O(log(max_int)),其中我们将执行位运算视作原子操作。
- 空间复杂度:O(1)。
博文参考
相关文章:

剑指 Offer 65. 不用加减乘除做加法
摘要 剑指 Offer 65. 不用加减乘除做加法 一、位运算 有符号整数通常用补码来表示和存储,补码具有如下特征: 正整数的补码与原码相同;负整数的补码为其原码除符号位外的所有位取反后加 11。可以将减法运算转化为补码的加法运算来实现。符…...

5年软件测试年薪30w+,我的坎坷之路谁又知道
在深圳做了五年软件测试工作,从之前的一脸懵的点点点,到现在会自动化测试,说一点点非计算机专业人员从事软件测试的心得体会,仅供参考交流。 大部分测试在公司没啥地位,当然如果你懂技术就还行,单纯点点点…...

【Opencv--自适应图像二值化】cv2.adaptiveThreshold()
【Opencv–adaptiveThreshold】自适应阈值图像二值化 文章目录【Opencv--adaptiveThreshold】自适应阈值图像二值化1. 介绍2. adaptiveThreshold函数2.1 函数调用2.2 补充说明3. 代码示例4. 效果4.1 原图(ori.img)4.2 处理后5. 参考1. 介绍 在这里 cv2.…...

洛谷P8601[蓝桥杯][2013年第四届真题]剪格子
题目描述如图 11 所示,33 的格子中填写了一些整数。我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 60。本题的要求就是请你编程判定:对给定的 mn 的格子中的整数,是否可以分割为两个部分,使…...

配置alias实现快速生成.gitignore文件
git工具:版本控制开发工具。 cscope工具:用于浏览C源码的工具,类似于ctags。在代码根目录下执行cscope -Rbq,然后产生三个索引文件(cscope.out、cscope.in.out和cscope.po.out三个文件)。 在Linux下使用vi…...

MySQL数据库调优————GROUP BY及DISTINCT优化
GROUP BY 三种处理GROUP BY的方式 松散索引扫描(Loose Index Scan)紧凑索引扫描(Tight Index Scan)临时表(Temporary table) 三种方式的性能一次递减 松散索引扫描 无需扫描满足条件的所有索引键即可返…...

LRU缓存算法
双向链表哈希表(非线程安全) https://leetcode.cn/problems/lru-cache/solutions/259678/lruhuan-cun-ji-zhi-by-leetcode-solution/ /*** LRU算法: 哈希表双向链表实现* 1. 双向链表按照被使用的顺序来存储, 靠近头部的节点是最近使用的, 靠近尾部的节…...

@Configuration注解
Configuration注解介绍 Configuration注解,用于标注一个类是一个spring的配置类(同时,也是一个bean),配置类中可以使用ComponentScan、Import、ImportResource 和 Bean等注解的方式定义beanDefinition。 Target(Elem…...

基于springboot+vue的食疗系统
基于springbootvue的食疗系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍&…...
sklearn学习-朴素贝叶斯
文章目录一、概述1、真正的概率分类器2、sklearn中的朴素贝叶斯二、不同分布下的贝叶斯1、高斯朴素贝叶斯GaussianNB2、探索贝叶斯:高斯朴素贝叶斯擅长的数据集3、探索贝叶斯:高斯朴素贝叶斯的拟合效果与运算速度总结一、概述 1、真正的概率分类器 算法…...

分享112个HTML艺术时尚模板,总有一款适合您
分享112个HTML艺术时尚模板,总有一款适合您 112个HTML艺术时尚模板下载链接:https://pan.baidu.com/s/1D3-mfPOud-f3vy9yLl-bmw?pwdfph2 提取码:fph2 Python采集代码下载链接:采集代码.zip - 蓝奏云 时尚平面模特网站模板 潮…...

用GDB远程调试运行于QEMU的程序
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 测试环境 本文使用 Ubuntu 16.04.4 LTS QEMU 环境进行调试。 3. 用 GDB 调试 QEMU 内程序 3.1 编写用来调试的程序 我们用 ARM32 来进行调试…...
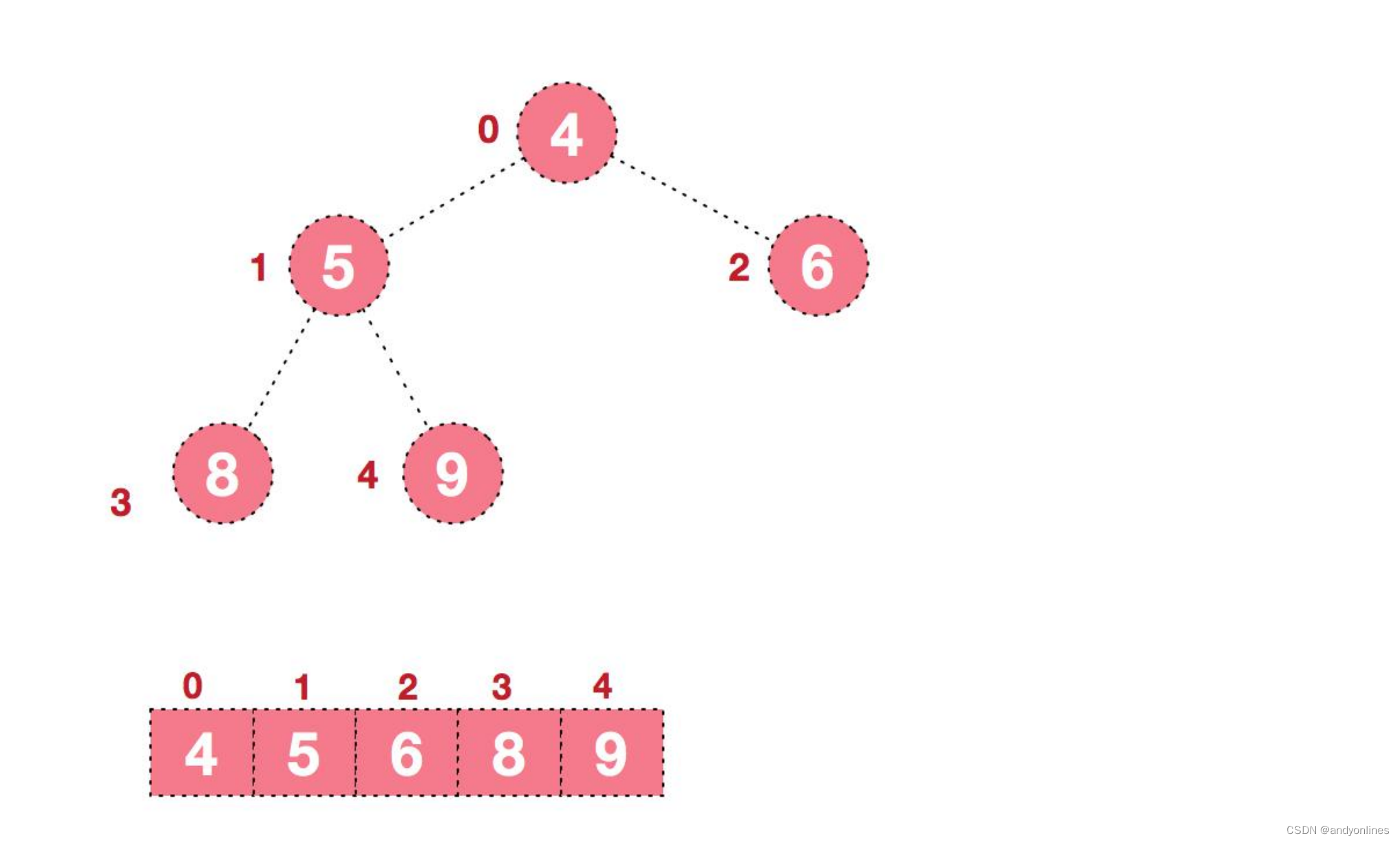
20 堆排序
文章目录1 堆排序的概念2 堆排序基本思想3 堆排序步骤图解说明4 堆排序的代码实现1 堆排序的概念 1) 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为 O(nlogn)…...
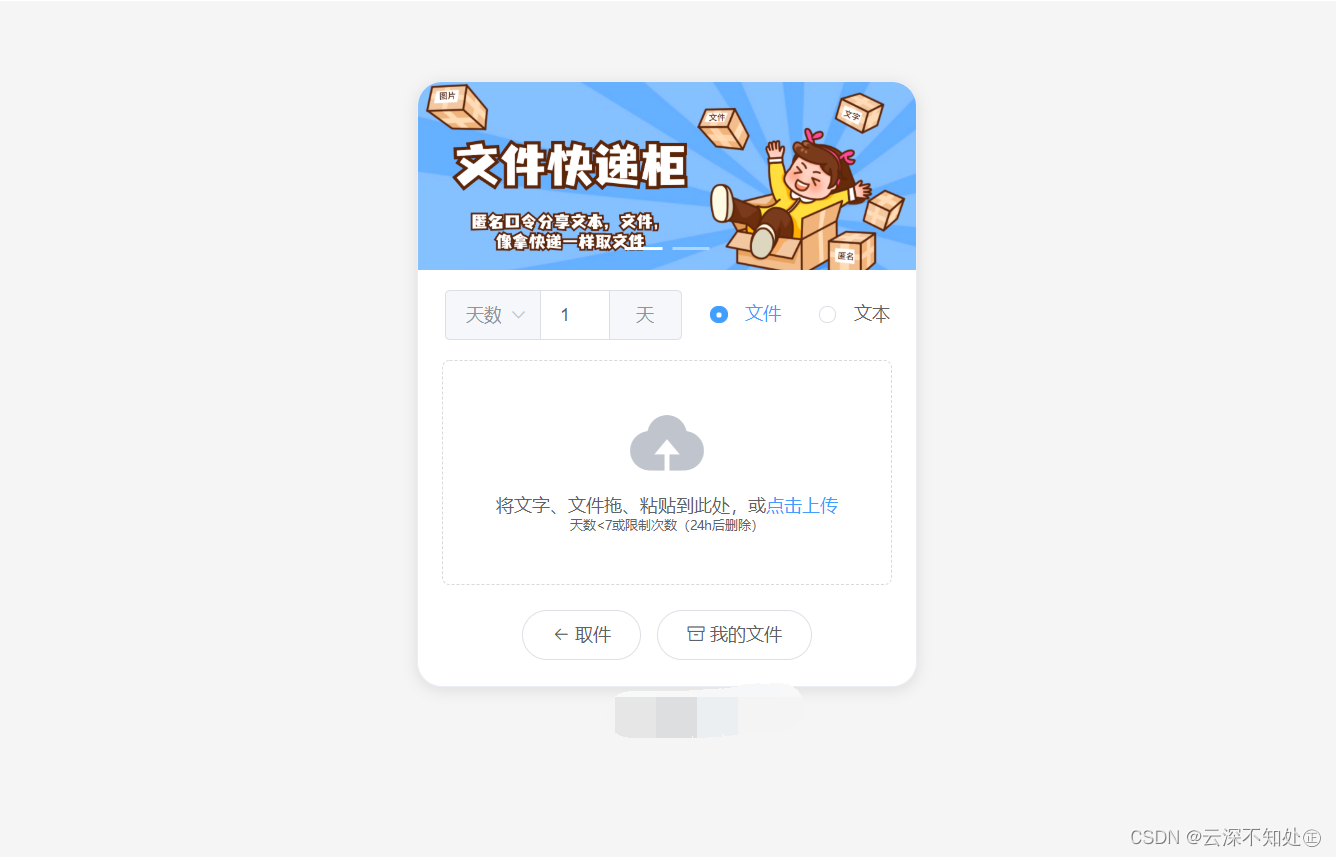
2023最新文件快递柜系统网站源码 | 匿名口令分享 | 临时文件分享
内容目录一、详细介绍二、效果展示1.部分代码2.效果图展示三、学习资料下载一、详细介绍 2023最新文件快递柜系统网站源码 | 匿名口令分享 | 临时文件分享 很多时候,我们都想将一些文件或文本传送给别人,或者跨端传递一些信息,但是我们又不…...
)
分片策略(二)
分片策略 基本概念 分片键 用于分片的字段,是将数据库或表拆分的字段,比如,我可以使用user_id作为分片键将用户数据分到不同的表中,这里的user_id就是分片键,除了这种单字段分片,ShardingSphere还支持多…...
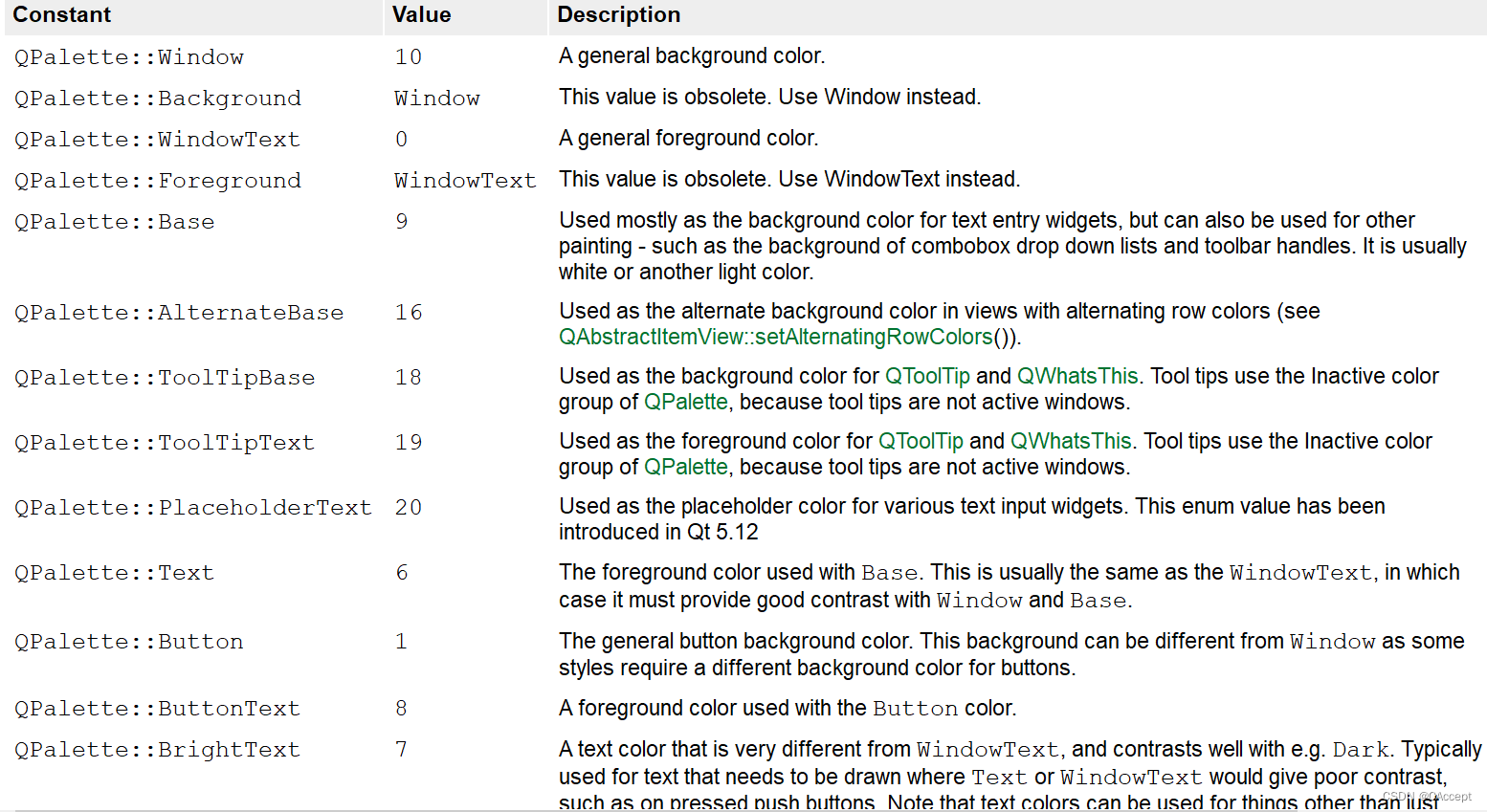
Qt之调色板类QPalette的使用
文章目录QPalette调色板类前言代码知识点讲解QPalette调色板类 前言 Qt提供的调色板类QPalette专门用于管理部件的外观显示,相当于部件或对话框的调色板,管理他们所有的颜色信息。每个部件都包含一个QPalette对象,在显示时,按照…...
Kotlin 32. Kotlin 多语言支持
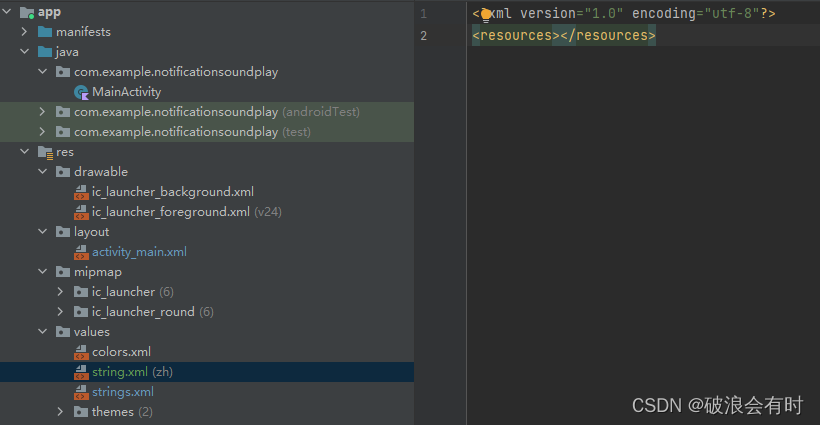
Kotlin 多语言支持 对于 Kotlin 来说,当我们新建一个项目时,会默认在 values/ 文件夹下,生成一个 strings.xml 文件。比如说, <resources><string name"app_name">exampleNewProject</string> <…...
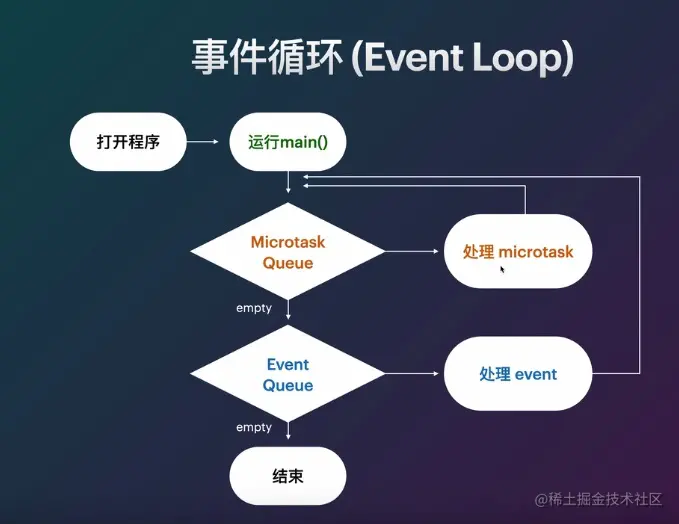
【Flutter入门到进阶】Dart进阶篇---DartVM单线程设计原理
1 虚拟机的指令执行设计 1.1 虚拟机的分类 基于栈的虚拟机,比如JVM虚拟机 基于寄存器的虚拟机,比如Dalvik虚拟机 1.2 虚拟机的概念 首先问一个基本的问题,作为一个虚拟机,它最基本的要实现哪些功能? 他应该能够模拟…...
的交集)
Dem和NvM(NVRAM Manager)的交集
NVRAM(NvM)提供了在NVRAM中存储数据Block的机制。 NVRAM Block(最大大小取决于配置)被分配给Dem,并由Dem实现事件状态信息和相关数据的永久存储(例如通电复位)。 ECU 状态管理器(Ec…...

AI神经网络CNN/RNN/DNN/SNN的区别对比
@版权声明: 本文由 ChatGpt 创作; BiliBili: https://www.bilibili.com/video/BV17D4y1P7pM/?share_source=copy_web&vd_source=6d217e0ff6387a749dc570aba51d36fd 引言 随着人工智能技术的发展,神经网络作为人工智能的核心技术之一,被广泛应用于图像识别、语音识别、…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
