ES6 Promise/Async/Await使用
Promise应用
在工作中, 我们经常会遇到用异步请求数据, 查询一个结果, 然后把返回的参数放入到下一个执行的异步函数像这样:
$.ajax({..., success(resp)=>{$.ajax({..., resp.id, success(resp)=>{$.ajax({..., resp.name success(resp)=>{//多层嵌套的情况, 看着是不是很难受}})}})
}})
当我们使用Promise后, 我们的程序就变成了这样:
let userInfo = ()=> {return new Promise((resolve, reject) => {console.log('查询用户信息...')resolve('王二')})
}let orderInfo = (userName)=> {return new Promise((resolve, reject) => {console.log(`查询用户${userName}的订单信息...`)resolve('ORDER_20230820000000001')})
}userInfo().then(resp=>{return orderInfo(resp)
}).then(resp=>{console.log(resp)
})
控制台输出如下:
查询用户信息...
查询用户王二的订单信息...
ORDER_20230820000000001
async/await应用
看是不是简洁很多了, 如果你不想使用这种链式调用, 也可以结合async/await来实现同步执行, 我们来稍微改一下userInfo函数, 让它模拟异步请求, 像下面这样:
let userInfo = ()=> {return new Promise((resolve, reject) => {console.log(new Date().toLocaleString()+' 查询用户信息...')//这里我们模拟异步请求, 等待三秒setTimeout(() => {resolve('王二')}, 3000)})
}let orderInfo = (userName)=> {return new Promise((resolve, reject) => {console.log(new Date().toLocaleString()+` 查询用户${userName}的订单信息...`)resolve('ORDER_20230820000000001')})
}let main = async ()=> {let user = await userInfo()let order = await orderInfo(user);console.log(new Date().toLocaleString()+' '+order)
}
main()
控制台输出如下:
2023/8/20 10:52:23 查询用户信息...
2023/8/20 10:52:26 查询用户王二的订单信息...
2023/8/20 10:52:26 ORDER_20230820000000001
注意看上面输出, 第一行和第二行是间隔3秒的, 说明是同步往下执行的, 这样修改之后程序是不是简洁很多呢, 对于日后维护起来也方便许多啦
异常处理
下面我们来看看如何进行异常处理, 在上面的栗子中我没有演示抛出异常和拒绝动作, 接下来看下如何处理异常和拒绝, 我们稍微改造一下代码, 像下面这样:
- 如果角色名称为空, 将抛出异常
- 如果角色等于zs, 拒绝, 无权查询
- 否则可以查询
let userInfo = (roleName)=> {return new Promise((resolve, reject) => {console.log(new Date().toLocaleString() + ' 查询用户信息...')if (!roleName) {// 这里模拟抛出异常throw new Error('参数为空,查询异常')} else if (roleName === 'zs') {//拒绝标识return reject('无权查询')}//这里我们模拟异步请求, 等待三秒setTimeout(() => {resolve('王二')}, 3000)})
}let main = async ()=> {try{//let user = await userInfo()let order = await orderInfo(user);console.log(new Date().toLocaleString()+' '+order)}catch (err) {//这里处理reject和error信息console.error(typeof err === 'object'?err.message:err)}}
main()
参数为空时输出:
2023/8/20 11:18:51 查询用户信息...
参数为空,查询异常
参数为zs时输出:
2023/8/20 11:19:12 查询用户信息...
无权查询
参数为admin时输出:
2023/8/20 11:19:46 查询用户信息...
2023/8/20 11:19:49 查询用户王二的订单信息...
2023/8/20 11:19:49 ORDER_20230820000000001
当然异常处理也可以用其他方式, 例如, 你可以在Promise提供的then和catch中处理, 像下面这样:
userInfo('').then(resp=>{return orderInfo(resp)
}, err=>{//这里处理reject和error信息console.error(typeof err === 'object'?err.message:err)
})
或者像这样
userInfo('zs').then(resp=>{return orderInfo(resp)
}).catch(err=>{//这里处理reject和error信息console.error(typeof err === 'object'?err.message:err)
})
怎么处理大家看自己习惯和实际需求吧
相关文章:

ES6 Promise/Async/Await使用
Promise应用 在工作中, 我们经常会遇到用异步请求数据, 查询一个结果, 然后把返回的参数放入到下一个执行的异步函数像这样: $.ajax({..., success(resp)>{$.ajax({..., resp.id, success(resp)>{$.ajax({..., resp.name success(resp)>{//多层嵌套的情况, 看着是不…...
Word中对象方法(Methods)的理解及示例(上)
【分享成果,随喜正能量】奋斗没有终点,任何时候都是一个起点,沉潜是为了蓄势待发,沉潜是为了等待因缘。鲸豚沉潜于大海,幽兰深藏于山谷,能够经得起沉潜的人,才会有更高的成就。正如一年的树木只能当柴烧&am…...
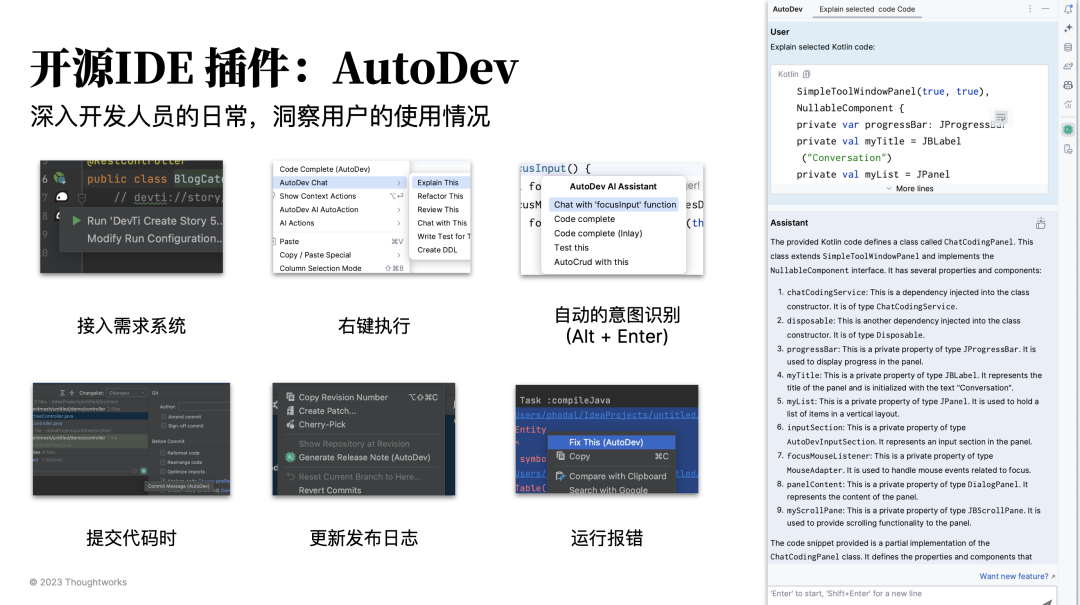
AutoDev 1.1.3 登场,个性化 AI 辅助:私有化大模型、自主设计 prompt、定义独特规则...
在过去的半个月里,我们为开源辅助编程工具 AutoDev 添加了更强大的自定义能力,现在你可以: 使用自己部署的开源大模型自己配置 Intellij IDEA 中的行为自定义开发过程中的规范 当然了,如果您自身拥有开发能力的话,建议…...

win11 python 调用edge调试过程
1、下载对应版本的驱动程序: https://developer.microsoft.com/zh-cn/microsoft-edge/tools/webdriver/ 2、和系统版本对应的exe文件(x86、x64要对应)放置的固定的目录,我放到了system32下了; 3、PATH路径添加windows/system32目录&#x…...

DS-排序回顾
快速排序相比于堆排序的优点有: 效率更高:快速排序的平均时间复杂度为 O(nlogn),而堆排序的时间复杂度为 O(nlogn)。虽然它们的时间复杂度相同,但是在实际情况下,快速排序往往比堆排序更快,因为快速排序具有…...
clion软件ide的安装和环境配置@ubuntu
1.官网: Download CLion 2.安装Clion 直接在官网下载并安装即可,过程很简单 https://www.jetbrains.com/clion/ https://www.jetbrains.com/clion/download/#sectionlinux 3.激活码 4.配置Clion 安装gcc、g、make Ubuntu中用到的编译工具是gcc©…...
Cpp学习——类与对象3
目录 一,初始化列表 1.初始化列表的使用 2.初始化列表的特点 3.必须要使用初始化列表的场景 二,单参数构造函数的隐式类型转换 1.内置类型的隐式类型转换 2. 自定义类型的隐式类型转换 3.多参数构造函数的隐式类型转换 4.当你不想要发生隐式类型转换…...

回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图&a…...
)
ahooks.js:一款强大的React Hooks库及其API使用教程(四)
一、ahooks.js简介二、ahooks.js安装三、继续ahooks.js API的介绍与使用教程51. useResetState52. useUpdateLayoutEffect53. useDeepCompareLayoutEffect54. useRafInterval55. useRafTimeout56. useTimeout57. useLockFn58. useDocumentVisibility59. useDrop60. useDrag 一、…...

FOSSASIA Summit 2023 - 开源亚洲行
作者 Ted 致歉:本来这篇博客早就该发出,但是由于前几个月频繁差旅导致精神不佳,再加上后续我又参加了 Linux 基金会 7/27 在瑞士日内瓦举办的 Open Source Congress,以及 7/29-30 台北的 COSCUP23,干脆三篇连发&#x…...
QT 基本对话框
包括: 1.标准文件对话框 dialog.h #ifndef DIALOG_H #define DIALOG_H#include <QDialog> #include <QTextCodec> #include <QLabel> #include <QLineEdit> #include <QPushButton> #include <QGridLayout> #include <QFr…...

8th参考文献:[8]许少辉.乡村振兴战略下传统村落文化旅游设计[M]北京:中国建筑出版传媒,2022.
8th参考文献:[8]许少辉.乡村振兴战略下传统村落文化旅游设计[M]北京:中国建筑出版传媒,2022&…...
Azure静态网站托管
什么是静态网站托管 Azure Blob的静态网站托管是一项功能,它允许开发人员在Azure Blob存储中托管和发布静态网站。通过这个功能,您可以轻松地将静态网页、图像、视频和其他网站资源存储在Azure Blob中,并直接通过提供的URL访问这些资源。 官…...
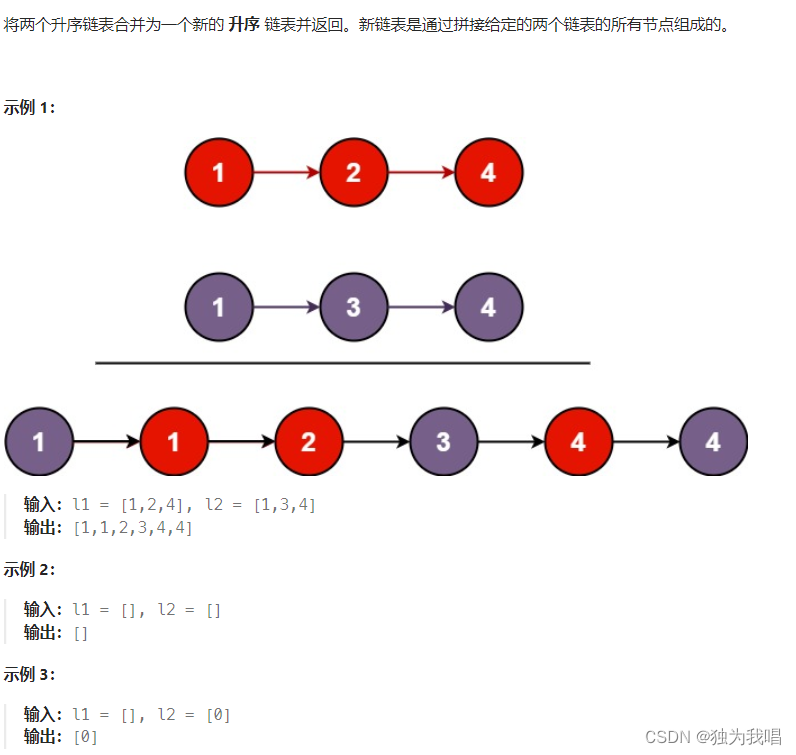
LeetCode 热题 100(五):54. 螺旋矩阵、234. 回文链表、21. 合并两个有序链表
题目一: 54. 螺旋矩阵https://leetcode.cn/problems/spiral-matrix/ 题目要求: 思路:一定要先找好边界。如下图 ,上边界是1234,右边界是8、12,下边界是9、10、11,左边界是5,所以可…...

常用消息中间件介绍
RocketMQ 阿里开源,阿里参照kafka设计的,Java实现 能够保证严格的消息顺序 提供针对消息的过滤功能 提供丰富的消息拉取模式 高效的订阅者水平扩展能力 实时的消息订阅机制 亿级消息堆积能力 RabbitMQ Erlang实现,非常重量级,更适…...
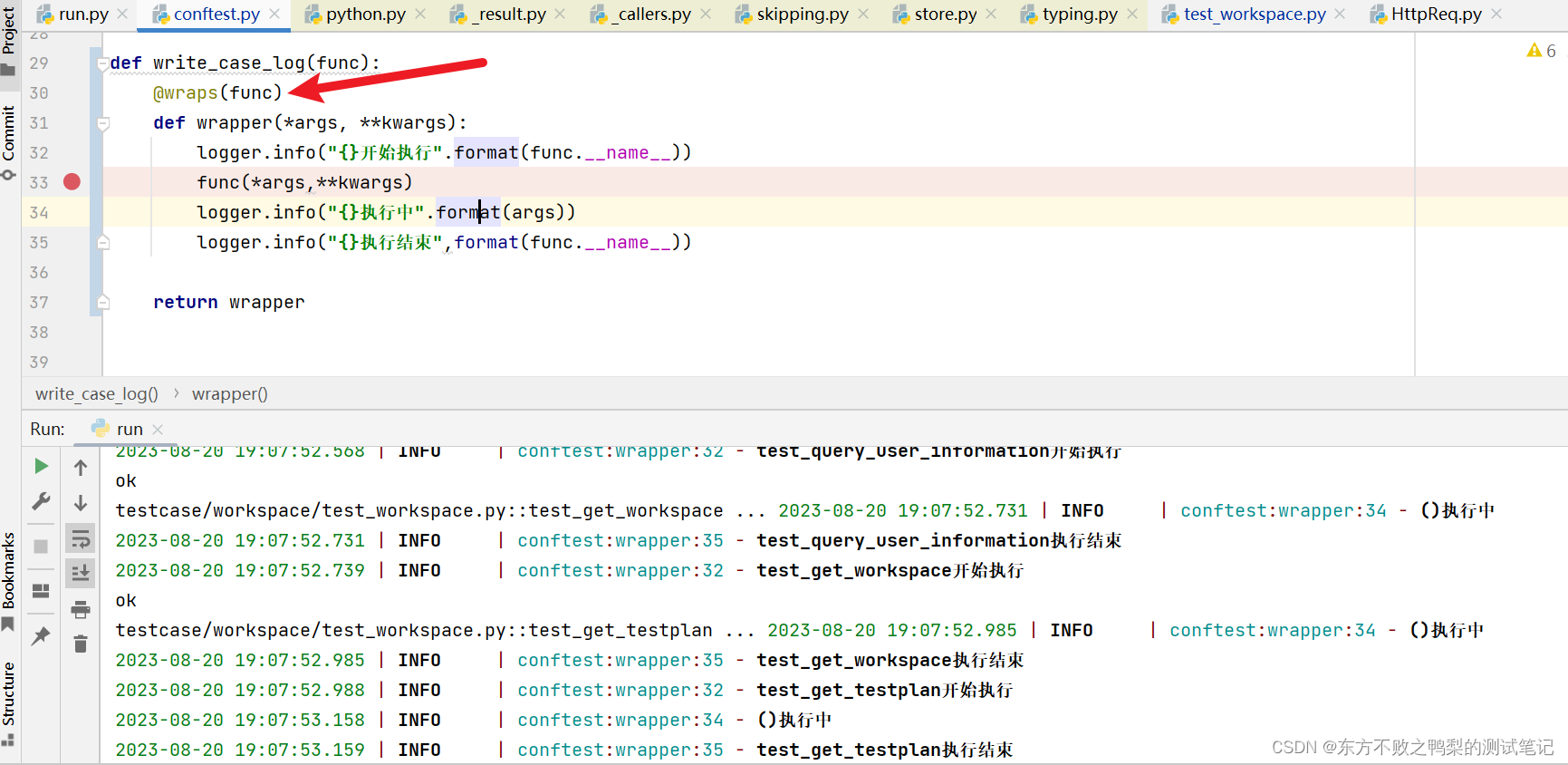
装饰器读取不到被装饰函数的参数-已解决
def write_case_log(func):def wrapper(*args, **kwargs):logger.info("{}开始执行".format(func.__name__))func(*args,**kwargs)logger.info("{}执行中".format(args))logger.info("{}执行结束",format(func.__name__))return wrapper被装饰函…...

python爬虫爬取中关村在线电脑以及参数数据
一. 内容简介 python爬虫爬取中关村在线电脑以及参数数据 二. 软件环境 2.1vsCode 2.2Anaconda version: conda 22.9.0 三.主要流程 3.1 代码 解析都在代码里面 # 接口分析 # 原始接口,后面几个数字就是占位的,每个位置代表着不同的标签 # http…...

chatGPT-对话爱因斯坦
引言 阿尔伯特爱因斯坦( 1879年 3 月 14 日 – 1955 年 4 月 18 日)是一位出生于德国的理论物理学家,被广泛认为成为有史以来最伟大、最有影响力的科学家之一。他以发展相对论而闻名,他还对量子力学做出了重要贡献,因…...

嵌入式软件开发中的数据类型转换
在嵌入式软件开发时,数据的显示必不可少,那么必定会涉及到数据类型转换。将不同类型的数据在编程中进行转换,以便满足不同的需求。 插入一个知识点: 在C语言中,字符串是由字符组成的字符数组,以null终止符…...
)
The Go Blog 01:反射的法则(译文)
反思的法则 罗伯-派克 2011 年 9 月 6 日 引言 计算机中的反射是指程序检查自身结构的能力,尤其是通过类型检查自身结构的能力;它是元编程的一种形式。它也是造成混乱的一个重要原因。 在本文中,我们试图通过解释 Go 中的反射是如何工作的…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...
