2023 CCPC 华为云计算挑战赛 hdu7401 流量监控(树形dp)
题目
流量监控 - HDU 7401 - Virtual Judge
简单来说,T(T<=20)组样例,sumn不超过2e4
每次给定一棵n(n<=2000)个点的树,两问:
①将n个点恰拆成n/2个pair(u,v),要求一个点是另一个点的祖先,求方案数
②若两个pair(u,v)、(w,x)满足:
u是v、w、x的祖先,w是v、x的祖先,v是x的祖先
即,四个点都在x通往根的路径上,且[u,v]和[w,x]相交,则称形成了一个区间交,
在①的所有合法方案数中,求区间交的总数
输出①、②的值,答案对998244353取模
思路来源
jiangly代码&heltion&tiger2005&夏老师
题解
对着jiangly代码,找了若干人讨论,终于讨论明白了
第一问,dp[i][j]表示i子树内当前有j个未匹配的点的方案数,
转移是一个树上背包,对子树做完树上背包之后,
再考虑u这个点的决策,要么是(,要么是)
换句话说,要么选一个之前未匹配的点进行匹配,要么新增一个未匹配的点
第二问,长度为4的祖先链(都在通往祖先的一条路径上),所以可以考虑把0-4都维护上,
这里实际是考虑每个长度为4的链的贡献,
即在dp的时候并不指定这四个点连的方式,只统计四元组的总方案数,
然后根据题目要求, 最后的时候将13相连、24相连
这相当于求从树上抠掉四个点(四个点在一条祖先链上)时,剩下的点构成合法方案的方案数
f[i][j][k]表示考虑到j的子树,当前抠掉了i个点,还有k个点没有匹配的方案数
相当于一个二维背包,i是一维,k是一维
转移先对u的子树v1、v2、...做背包,做k这一维的背包,
又因为不同子树之间的点并不在一条祖先链上,
所以i这一维做背包两两合并的时候,两棵子树的i这一维不能同时大于0
rep(a,0,4){rep(b,0,4){if(a && b)continue;rep(i,0,sz[u]){rep(j,0,sz[v]){add(tmp[a+b][i+j],1ll*f[a][u][i]*f[b][v][j]%mod);}}}}将子树都合并进来之后,再考虑u的决策,
u的决策实际有三种, 要么是(,要么是),要么从树上抠掉
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,ll> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=2e3+10,mod=998244353,inv2=(mod+1)/2;
int T,n,u,v,sz[N],tmp[5][N],f[5][N][N];
vector<int>e[N];
void add(int &x,int y){x=(x+y)%mod;
}
void dfs(int u,int fa){sz[u]=1;f[0][u][0]=1;for(auto &v:e[u]){if(v==fa)continue;dfs(v,u);memset(tmp,0,sizeof tmp);rep(a,0,4){rep(b,0,4){if(a && b)continue;rep(i,0,sz[u]){rep(j,0,sz[v]){add(tmp[a+b][i+j],1ll*f[a][u][i]*f[b][v][j]%mod);}}}}sz[u]+=sz[v];rep(a,0,4){rep(i,0,sz[u]){f[a][u][i]=tmp[a][i];}}}memset(tmp,0,sizeof tmp);rep(a,0,4){rep(i,0,sz[u]){if(i)add(tmp[a][i-1],1ll*f[a][u][i]*i%mod);add(tmp[a][i+1],f[a][u][i]);if(a<4)add(tmp[a+1][i],f[a][u][i]);}}rep(a,0,4){rep(i,0,sz[u]){f[a][u][i]=tmp[a][i];}}
}
int main(){scanf("%d",&T);while(T--){sci(n);rep(i,1,n){e[i].clear();sz[i]=0;}memset(f,0,sizeof f);rep(i,2,n){sci(u),sci(v);e[u].pb(v);e[v].pb(u);}dfs(1,0);printf("%d %d\n",f[0][1][0],f[4][1][0]);}return 0;
}相关文章:
)
2023 CCPC 华为云计算挑战赛 hdu7401 流量监控(树形dp)
题目 流量监控 - HDU 7401 - Virtual Judge 简单来说,T(T<20)组样例,sumn不超过2e4 每次给定一棵n(n<2000)个点的树,两问: ①将n个点恰拆成n/2个pair(u,v),要求一个点是另一个点的祖先,求方案数 …...
01.Django入门
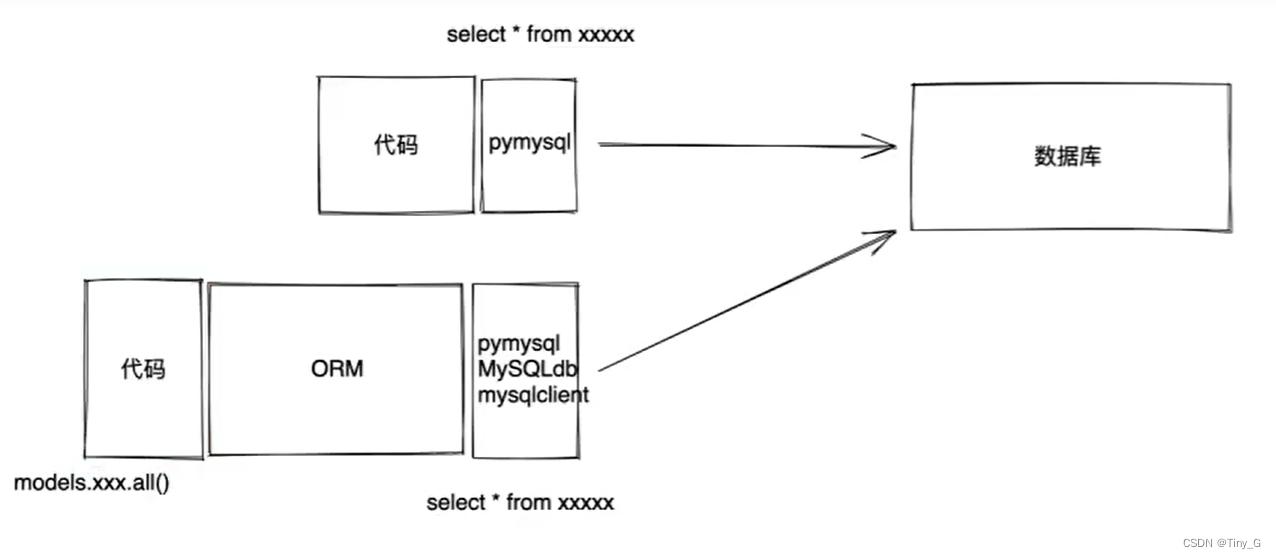
1.创建项目 1.1基于终端创建Django项目 打开终端进入文件路径(打算将项目放在哪个目录,就进入哪个目录) E:\learning\python\Django 执行命令创建项目 F:\Anaconda3\envs\pythonWeb\Scripts\django-admin.exe(Django-admin.exe所…...
亿赛通电子文档安全管理系统任意文件上传漏洞(2023-HW)
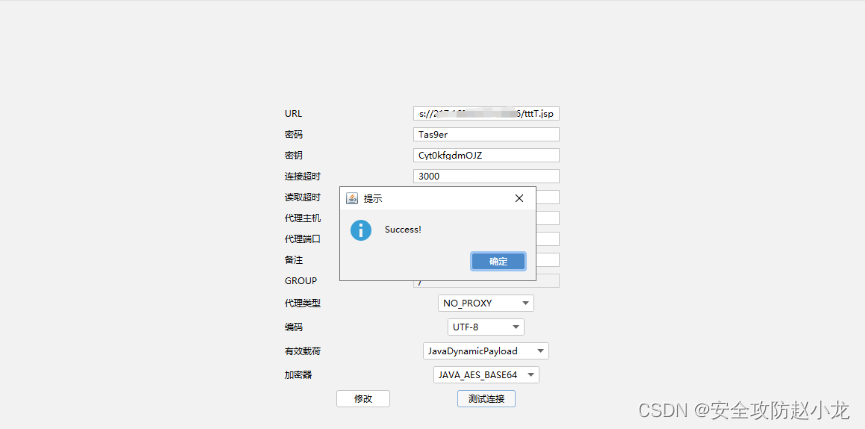
亿赛通电子文档安全管理系统任意文件上传漏洞 一、 产品简介二、 漏洞概述三、 影响范围四、 复现环境五、 漏洞复现小龙POC检测 免责声明:请勿利用文章内的相关技术从事非法测试,由于传播、利用此文所提供的信息或者工具而造成的任何直接或者间接的后果…...
docker限制容器日志大小
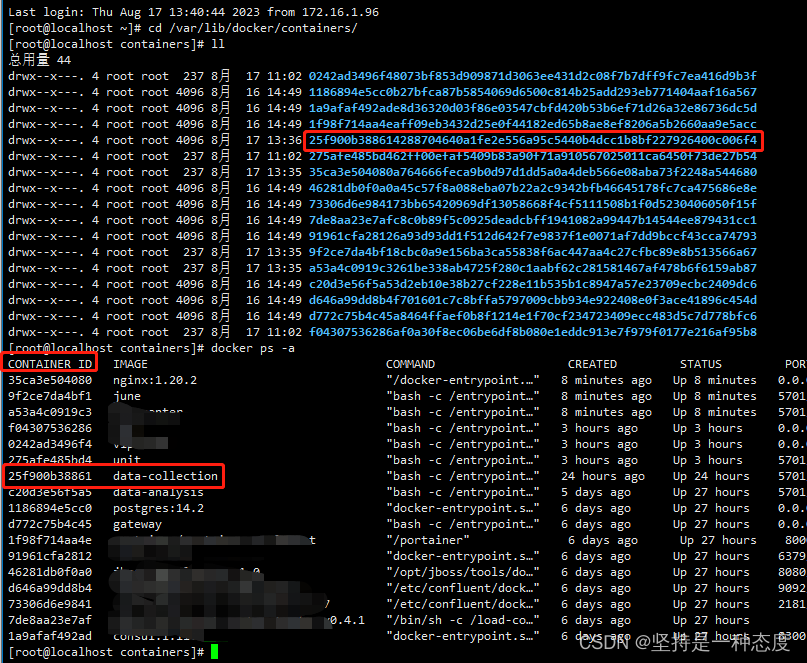
文章目录 业务场景问题排查彻底解决 业务场景 我们公司做交通相关业务,我们部门主要负责信控服务,卖信号机的硬件产品和配套的信控平台 由于有部分小项目,可能只有几十个路口,客户预算有限,只给我们老旧的Windows ser…...

底层驱动实现数码管显示温湿度数值功能
开发板:STM32MP157A 温湿度传感器:si7006 显示器(数码管):m74hc595 遇到的问题:循环采集温湿度传感器数值,并将数值发送给数码管的时候两者存在竞态关系,导致数码管显示亮度很暗 …...

03架构管理之测试管理
专栏说明:针对于企业的架构管理岗位,分享架构管理岗位的职责,工作内容,指导架构师如何完成架构管理工作,完成架构师到架构管理者的转变。计划以10篇博客阐述清楚架构管理工作,专栏名称:架构管理…...
的知识)
30、devtools 依赖关于自动重启(自动加载页面)的知识
devtools 依赖关于自动重启的知识 ★ 自动重启 devtools会监控类加载路径中的文件(尤其是*.class文件),只要这些文件发生了改变, devtools就会自动重启Spring Boot应用。▲ 不同工具触发自动重启的方式:Eclipse&…...

ES6 Promise/Async/Await使用
Promise应用 在工作中, 我们经常会遇到用异步请求数据, 查询一个结果, 然后把返回的参数放入到下一个执行的异步函数像这样: $.ajax({..., success(resp)>{$.ajax({..., resp.id, success(resp)>{$.ajax({..., resp.name success(resp)>{//多层嵌套的情况, 看着是不…...
Word中对象方法(Methods)的理解及示例(上)
【分享成果,随喜正能量】奋斗没有终点,任何时候都是一个起点,沉潜是为了蓄势待发,沉潜是为了等待因缘。鲸豚沉潜于大海,幽兰深藏于山谷,能够经得起沉潜的人,才会有更高的成就。正如一年的树木只能当柴烧&am…...
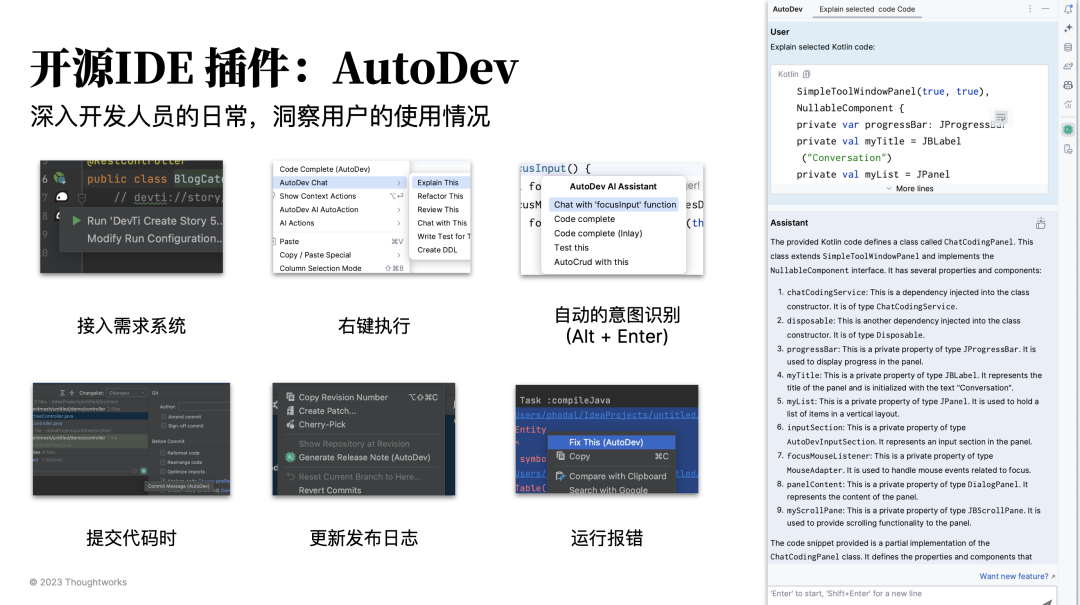
AutoDev 1.1.3 登场,个性化 AI 辅助:私有化大模型、自主设计 prompt、定义独特规则...
在过去的半个月里,我们为开源辅助编程工具 AutoDev 添加了更强大的自定义能力,现在你可以: 使用自己部署的开源大模型自己配置 Intellij IDEA 中的行为自定义开发过程中的规范 当然了,如果您自身拥有开发能力的话,建议…...

win11 python 调用edge调试过程
1、下载对应版本的驱动程序: https://developer.microsoft.com/zh-cn/microsoft-edge/tools/webdriver/ 2、和系统版本对应的exe文件(x86、x64要对应)放置的固定的目录,我放到了system32下了; 3、PATH路径添加windows/system32目录&#x…...

DS-排序回顾
快速排序相比于堆排序的优点有: 效率更高:快速排序的平均时间复杂度为 O(nlogn),而堆排序的时间复杂度为 O(nlogn)。虽然它们的时间复杂度相同,但是在实际情况下,快速排序往往比堆排序更快,因为快速排序具有…...
clion软件ide的安装和环境配置@ubuntu
1.官网: Download CLion 2.安装Clion 直接在官网下载并安装即可,过程很简单 https://www.jetbrains.com/clion/ https://www.jetbrains.com/clion/download/#sectionlinux 3.激活码 4.配置Clion 安装gcc、g、make Ubuntu中用到的编译工具是gcc©…...
Cpp学习——类与对象3
目录 一,初始化列表 1.初始化列表的使用 2.初始化列表的特点 3.必须要使用初始化列表的场景 二,单参数构造函数的隐式类型转换 1.内置类型的隐式类型转换 2. 自定义类型的隐式类型转换 3.多参数构造函数的隐式类型转换 4.当你不想要发生隐式类型转换…...

回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现PSO-RBF粒子群优化算法优化径向基函数神经网络多输入单输出回归预测(多指标,多图&a…...
)
ahooks.js:一款强大的React Hooks库及其API使用教程(四)
一、ahooks.js简介二、ahooks.js安装三、继续ahooks.js API的介绍与使用教程51. useResetState52. useUpdateLayoutEffect53. useDeepCompareLayoutEffect54. useRafInterval55. useRafTimeout56. useTimeout57. useLockFn58. useDocumentVisibility59. useDrop60. useDrag 一、…...

FOSSASIA Summit 2023 - 开源亚洲行
作者 Ted 致歉:本来这篇博客早就该发出,但是由于前几个月频繁差旅导致精神不佳,再加上后续我又参加了 Linux 基金会 7/27 在瑞士日内瓦举办的 Open Source Congress,以及 7/29-30 台北的 COSCUP23,干脆三篇连发&#x…...
QT 基本对话框
包括: 1.标准文件对话框 dialog.h #ifndef DIALOG_H #define DIALOG_H#include <QDialog> #include <QTextCodec> #include <QLabel> #include <QLineEdit> #include <QPushButton> #include <QGridLayout> #include <QFr…...

8th参考文献:[8]许少辉.乡村振兴战略下传统村落文化旅游设计[M]北京:中国建筑出版传媒,2022.
8th参考文献:[8]许少辉.乡村振兴战略下传统村落文化旅游设计[M]北京:中国建筑出版传媒,2022&…...
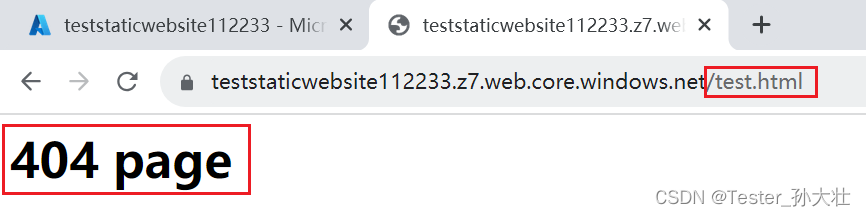
Azure静态网站托管
什么是静态网站托管 Azure Blob的静态网站托管是一项功能,它允许开发人员在Azure Blob存储中托管和发布静态网站。通过这个功能,您可以轻松地将静态网页、图像、视频和其他网站资源存储在Azure Blob中,并直接通过提供的URL访问这些资源。 官…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
