07无监督学习——降维
1.降维的概述
维数灾难(Curse of Dimensionality):通常是指在涉及到向量的计算的问题中,随着维数的增加,计算量呈指数倍增长的一种现象。
1.1什么是降维?
1.降维(Dimensionality Reduction)是将训练数据中的样本(实例)从高维空间转换到低维空间。
2.有很多种算法可以完成对原始数据的降维,在这些方法中,降维是通过对原始数据的线性变换实现的。
1.2为什么要降维?
1.高维数据增加了运算的难度,维度越高,算法的搜索难度。
2.高维使得学习算法的泛化能力变弱,降维能够增加数据的可读性,利于发掘数据的有意义的结构。
1.3降维的主要作用:
-
减少冗余特征,降低数据维度
-
数据可视化
降维的优点:
- 通过减少特征的维数,数据集存储所需的空间也相应减少,减少了特征维数所需的计算训练时间;
- 数据集特征的降维有助于快速可视化数据;
- 通过处理多重共线性消除冗余特征。
降维的缺点:
- 由于降维可能会丢失一些数据;
- 在主成分分析(PCA)降维技术中,有时需要考虑多少主成分是难以确定的,往往使用经验法则
2.奇异值分解
奇异值分解(Singular Value Decomposition,以下简称SVD)是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。是很多机器学习算法的基石。
sVD可以将一个矩阵A分解为三个矩阵的乘积:
一个正交矩阵U(orthogonal matrix),
一个对角矩阵(diagonal matrix) Σ \Sigma Σ
一个正交矩阵V的转置
分解的作用:线性变换 = 旋转 + 拉伸 +旋转
SVD分解可以将一个矩阵进行分解,对角矩阵对角线上的特征值递减存放,而且奇异值的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。
也就是说,对于奇异值,它跟我们特征分解中的特征值类似,我们也可以用最大的k 个的奇异值和对应的左右奇异向量来近似描述矩阵。
3.主成分分析
主成分分析( Principal Component Analysis,PCA )是一种降维方法,通过将一个大的特征集转换成一个较小的特征集,这个特征集仍然包含了原始数据中的大部分信息,从而降低了原始数据的维数。
减少一个数据集的特征数量自然是以牺牲准确性为代价的,但降维的诀窍是用一点准确性换取简单性。因为更小的数据集更容易探索和可视化,并且对于机器学习算法来说,分析数据会更快、更容易,而不需要处理额外的特征。
PCA识别在训练集中占最大方差量的轴。
PCA的算法两种实现方法:
(1)基于SVD分解协方差矩阵实现PCA算法
PCA 减少n维到lk维·
设有m条n维数据将原始数据按列组成n行m列矩阵X
第一步是均值归一化。我们需要计算出所有特征的均值和标准差,然后做Z值化。
第二步是计算协方差矩阵( covariance matrix )) Σ \Sigma Σ,其特征向量就是我们要求解的主成分。
(2)基于特征值分解协方差矩阵实现PCA算法
PCA减少n维到k 维:
设有m条n维数据,将原始数据按列组成n 行m列矩阵X
第一步是均值归一化。我们需要计算出所有特征的均值和标准差,然后做z值化。
第二步是计算协方差矩阵(covariance matrix)2,其特征向量就是我们要求解的主成分。特征值分解矩阵
对于矩阵A,有一组特征向量v,将这组向量进行正交化单位化,就能得到一组交单位向量。特征值分解,就是将矩阵A 分解为如下式:
A = P Σ P − 1 {\rm{A = P}}\Sigma {P^{^{ - 1}}} A=PΣP−1
其中,Р是矩阵A的特征向量组成的矩阵,习则是一个对角阵,对角线上的元素就是特征值。
PCA的缺点:
PCA追求的是在降维之后能够最大化保持数据的内在信息,并通过衡量在投影方向上的数据方差的大小来衡量该方向的重要性。但是这样投影以后对数据的区分作用并不大,反而可能使得数据点揉杂在一起无法区分。
这也是PCA存在的最大一个问题,这导致使用PCA在很多情况下的分类效果并不好。
4.t-分布领域嵌入算法t-SNE(t-distributedstochastic neighbor embedding)
步骤:
- 数据跟PCA一样在处理之前先做归一化
- 在低维空间中计算数据所有点与某个点的相似度
- 将其在映射在t分布函数的横轴上
- 计算高维度与低纬度的相似度矩阵的差异,设计loss function,然后用梯度下降来优化它
相关文章:

07无监督学习——降维
1.降维的概述 维数灾难(Curse of Dimensionality):通常是指在涉及到向量的计算的问题中,随着维数的增加,计算量呈指数倍增长的一种现象。 1.1什么是降维? 1.降维(Dimensionality Reduction)是将训练数据中的样本(实例)从高维空间转换到低维…...
)
系列七、IOC操作bean管理(xml自动装配)
一、概述 自动装配是根据指定规则(属性名称或者属性类型),Spring自动将匹配的属性值进行注入。 二、分类 xml自动装配分为按照属性名称自动装配(byName)和按照属性类型自动装配(byType)。 2.1…...
01- vdom 和模板编译源码
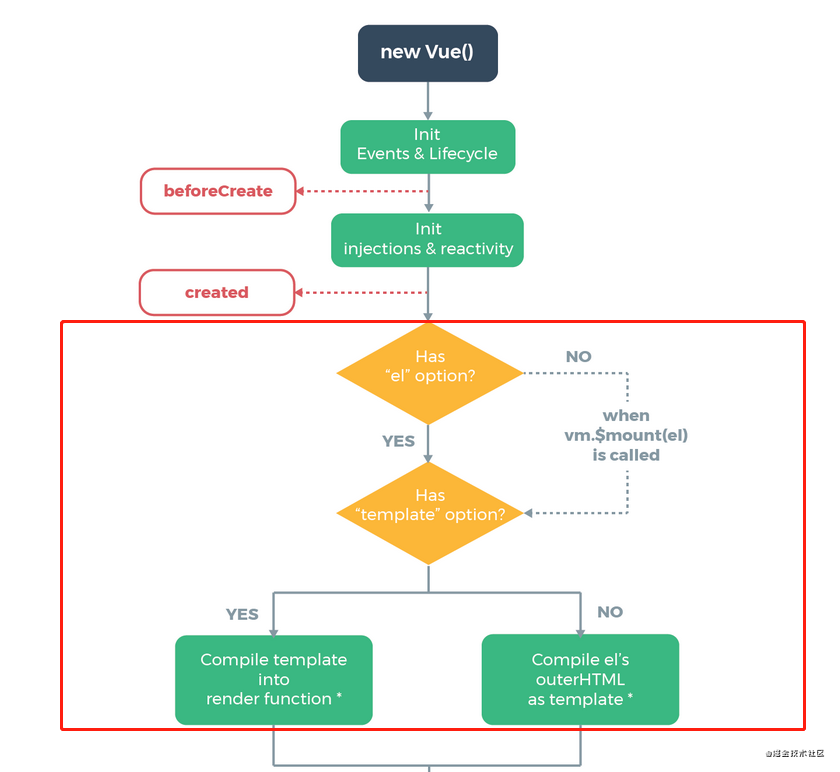
组件渲染的过程 template --> ast --> render --> vDom --> 真实的Dom --> 页面 Runtime-Compiler和Runtime-Only的区别 - 简书 编译步骤 模板编译是Vue中比较核心的一部分。关于 Vue 编译原理这块的整体逻辑主要分三个部分,也可以说是分三步&am…...

C++入门知识点——解决C语言不足
😶🌫️Take your time ! 😶🌫️ 💥个人主页:🔥🔥🔥大魔王🔥🔥🔥 💥代码仓库:🔥🔥魔…...

探秘分布式大数据:融合专业洞见,燃起趣味火花,启迪玄幻思维
文章目录 一 数据导论二 大数据的诞生三 大数据概论3.1 大数据的5V特征3.2 大数据的工作核心 四 大数据软件生态4.1 数据存储软件4.2 数据计算软件4.3 数据传输软件 五 Apache Hadoop概述5.1 Apache Hadoop框架5.2 Hadoop的功能5.3 Hadoop的发展5.4 Hadoop发行版本 一 数据导论…...

什么是 SPI,和API有什么区别?
面试回答 Java 中区分 API 和 SPI,通俗的讲:API 和 SPI 都是相对的概念,他们的差别只在语义上,API 直接被应用开发人员使用,SPI 被框架扩展人员使用。 API Application Programming Interface 大多数情况下ÿ…...
 失败)
python3 安装clickhouse_sqlalchemy(greenlet) 失败
环境信息: centos7操作系统,python3.8 执行pip3 install clickhouse_sqlalchemy或者pip3 install greenlet报以下报错: Command "/opt/python3.6.10-customized/bin/python3.6 -u -c "import setuptools, tokenize;file/tmp/pip-in…...

五款拿来就能用的炫酷表白代码
「作者主页」:士别三日wyx 「作者简介」:CSDN top100、阿里云博客专家、华为云享专家、网络安全领域优质创作者 「推荐专栏」:小白零基础《Python入门到精通》 五款炫酷表白代码 1、无限弹窗表白2、做我女朋友好吗,不同意就关机3、…...

Springboot 封装整活 Mybatis 动态查询条件SQL自动组装拼接
前言 ps:最近在参与3100保卫战,战况很激烈,刚刚打完仗,来更新一下之前写了一半的博客。 该篇针对日常写查询的时候,那些动态条件sql 做个简单的封装,自动生成(抛砖引玉,搞个小玩具&a…...

宝塔部署Java+Vue前后端分离项目经验总结
前言 之前部署服务器都是在Linux环境下自己一点一点安装软件,听说用宝塔傻瓜式部署更快,这次浅浅尝试了一把。 确实简单! 1、 买服务器 咋买服务器略,记得服务器装系统就装 Cent OS 7系列即可,我装的7.6。 2、创建…...

【公告】停止更新
CSDN 博客的限制太多了。阅读体验也非常差。后续将不再 CSDN 上更新。 逐步迁移到掘金和个人博客。 欢迎关注 掘金:0xforee 个人博客:0xforee’s blog...
AutoHotKey+VSCode开发扩展推荐
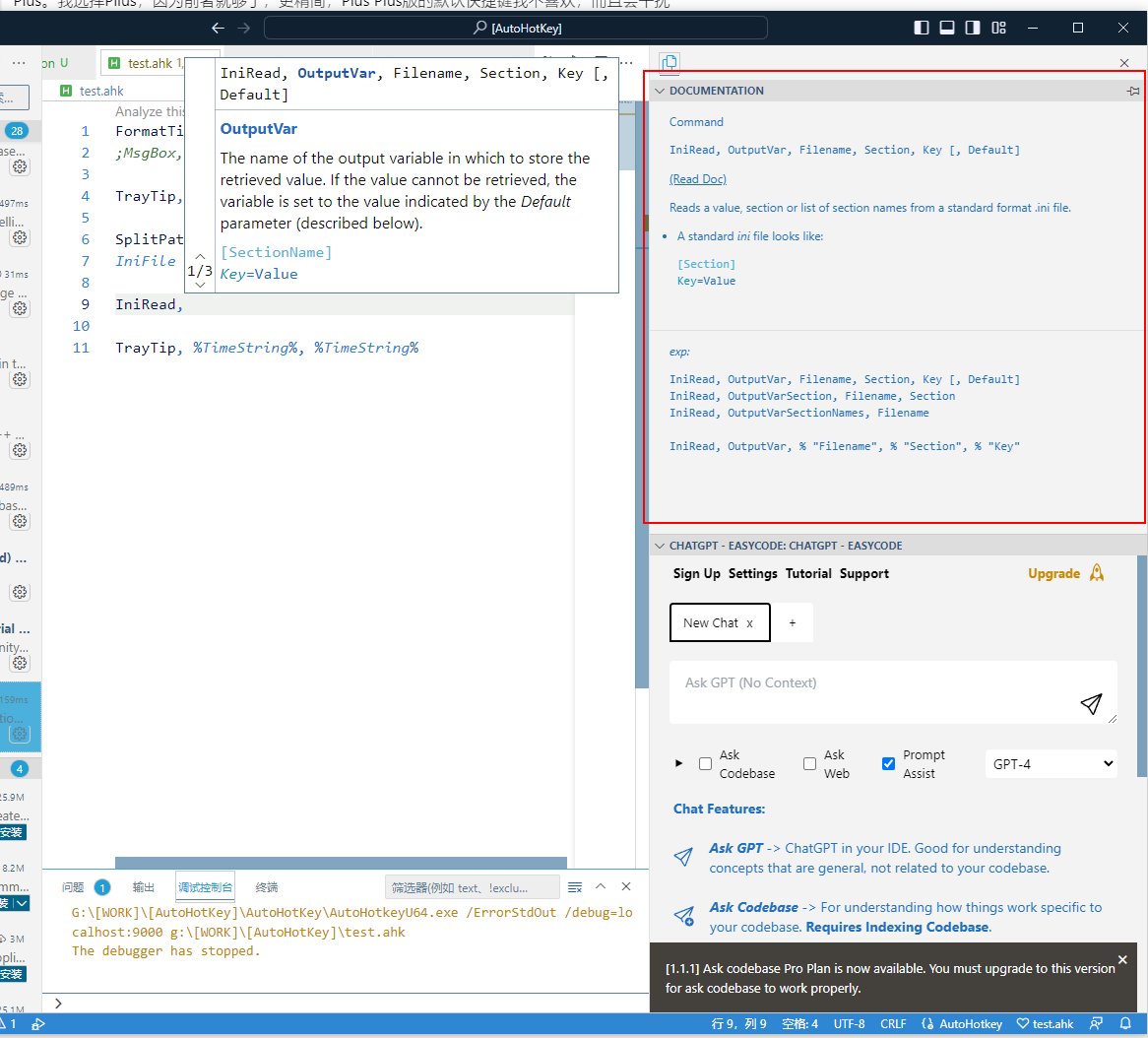
原来一直用的大众推荐的SciTeAHK版,最近发现VSCode更舒服一些,有几个必装的扩展推荐一下: AutoHotkey Plus 请注意不是AutoHotkey Plus Plus。如果在扩展商店里搜索会有两个,一个是Plus,一个是Plus Plus。我选择Pllus&…...

了解 JSON 格式
一、JSON 基础 JSON(JavaScript Object Notation,JavaScript 对象表示法)是一种轻量级的数据交换格式,JSON 的设计目的是使得数据的存储和交换变得简单。 JSON 易于人的阅读和书写,同时也易于机器的解析和生成。尽管 J…...

[RDMA] 高性能异步的消息传递和RPC :Accelio
1. Introduce Accelio是一个高性能异步的可靠消息传递和RPC库,能优化硬件加速。 RDMA和TCP / IP传输被实现,并且其他的传输也能被实现,如共享存储器可以利用这个高效和方便的API的优点。Accelio 是 Mellanox 公司的RDMA中间件,用…...
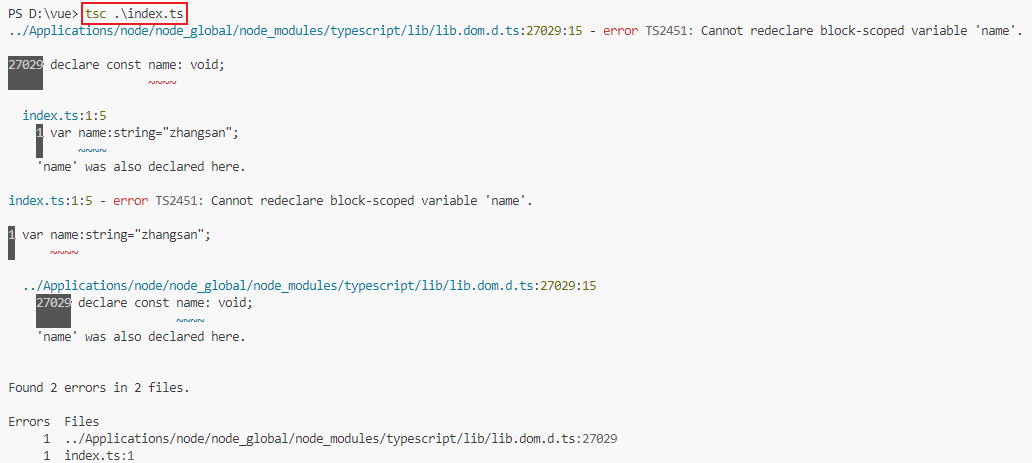
typescript报错:‘name‘ was also declared here
问题再现 用 Typescript 时, 遇到一个声明常量 name 的报错。代码如下: let name:string"zhangsan"; let num:number1001;执行编译时报错: 原因 在默认状态下,typescript 将 DOM typings 作为全局的运行环境&#…...

第十章:联邦学习视觉案例
代码 传送门...
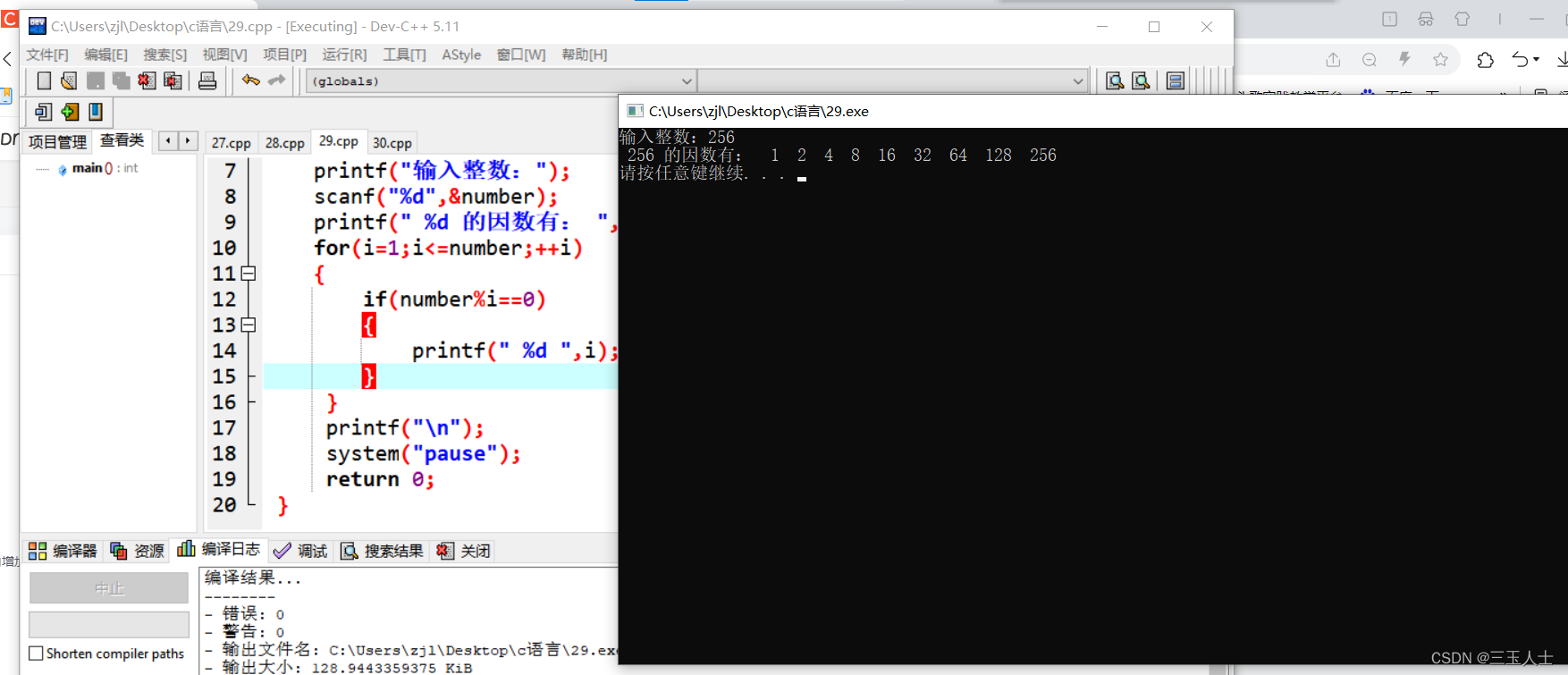
c语言——输出一个整数的所有因数
//输出一个整数的所有因数 #include<stdio.h> #include<stdlib.h> int main() {int number,i;printf("输入整数:");scanf("%d",&number);printf(" %d 的因数有: ",number);for(i1;i<number;i){if(numb…...
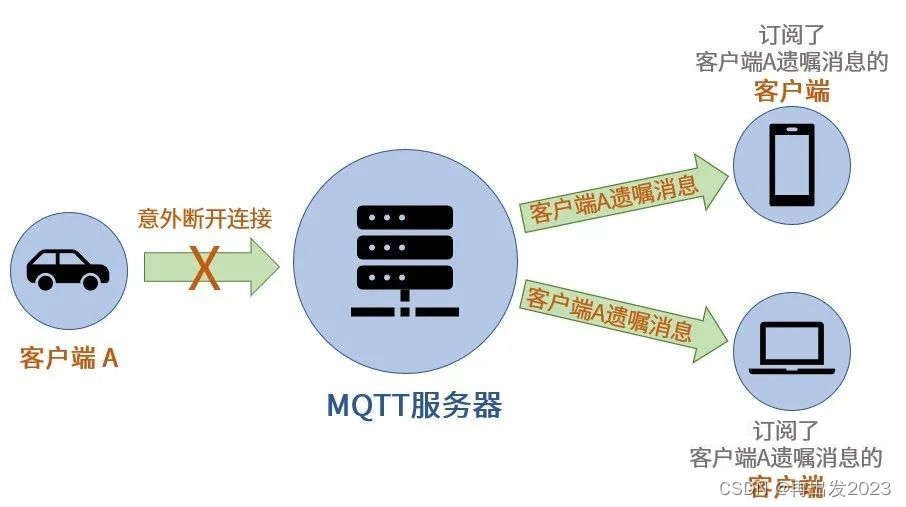
mqtt学习记录
目录 1 匿名登录2 ⽤户名密码登录,配置接收的主题mosquitto 配置文件修改添加⽤户信息添加topic和⽤户的关系登录演示 3 遗嘱机制 1 匿名登录 ⾸先打开三个终端, 启动代理服务:mosquitto -v -v 详细模式 打印调试信息 默认占⽤:…...

爬虫逆向实战(十八)--某得科技登录
一、数据接口分析 主页地址:某得科技 1、抓包 通过抓包可以发现数据接口是AjaxLogin 2、判断是否有加密参数 请求参数是否加密? 查看“载荷”模块可以发现有一个password加密参数和一个__RequestVerificationToken 请求头是否加密? 无…...
Java-数组
什么是数组 数组:可以看成是相同类型元素的一个集合。在内存中是一段连续的空间。 在java中, 数组中存放的元素其类型相同数组的空间是连在一起的每个空间有自己的编号,起始位置的编号为0,即数组的下标。 数组的创建及初始化 数…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...
