什么是视频的编码和解码
这段描述中,视频解码能力和视频编码能力指的是不同的处理过程。视频解码是将压缩过的视频数据解开并还原为可播放的视频流,而视频编码是将原始视频数据压缩成更小的尺寸,以减少存储空间和传输带宽。在这个上下文中,解码能力和编码能力的区别如下:
-
视频解码能力: 这个机器具备960fps 1080p(32路1080P@30FPS)的视频解码能力。这意味着它可以同时解码高达32个1080P分辨率的视频流,每个视频流的帧率为30帧/秒。这样的能力对于实时监控、视频分析等应用非常有用。
-
视频编码能力: 机器拥有50fps 1080p(2路1080P@25FPS)的视频编码能力。这表示它可以同时对两个1080P分辨率的视频流进行编码,每个视频流的帧率为25帧/秒。视频编码通常用于将视频压缩为更小的文件大小,以便存储或传输。
总之,视频解码能力用于解开已经压缩的视频流,使其可播放和分析,而视频编码能力则用于将视频压缩,以减少占用的存储空间和传输所需的带宽。这两种能力在不同的应用场景中都非常重要
在算法处理视频流的过程中,抽帧成图片进行识别和处理属于解码过程。解码是将压缩的视频数据还原成可识别和处理的图像帧。当从视频流中抽取图像帧以进行识别和处理时,实际上是在解码这些图像帧,将它们从压缩格式还原为可用的图像数据,以便进行后续的算法处理。视频编码和解码是两个相互关联的过程,但在这种情况下,你提到的抽帧和处理是发生在解码阶段。
编码通常发生在算法处理后,当需要将处理过的数据进行压缩以减少存储空间或传输带宽时。一旦算法对图像或视频进行了处理,生成了一些数据,这些数据可以进一步被编码成更紧凑的格式,以便在存储或传输过程中占用更少的资源。编码过程会将原始数据转换成压缩编码,使其占用的空间更小,同时仍然能够在解码后恢复为原始数据,以便进一步的处理或回放是的,如果将未压缩的视频抽帧并将其转换为单独的图像,这个过程通常被称为解码。在这种情况下,图像帧并没有经过压缩,因此没有需要解码的压缩编码。相反,将视频帧转换为图像涉及解析视频流中的原始图像数据,以便将其表示为图像文件或图像数据供进一步处理很抱歉,由于我无法在文本聊天中进行图形绘制,无法为您绘制流程图。但是我可以为您提供一个文字描述的流程图:
-
视频编码过程:
- 原始图像帧 -> 编码器 -> 压缩编码格式
- 图像帧经过压缩编码器,使用特定的压缩算法,转换成紧凑的编码格式。编码后的数据可以在存储和传输中节省空间和带宽。
-
视频解码过程:
- 压缩编码格式 -> 解码器 -> 原始图像帧
- 编码后的数据通过解码器,使用逆向的解码算法,转换回原始的图像帧。解码后的数据可以用于播放、编辑或进一步处理。
总之,视频编码和解码是互相补充的过程,允许在存储、传输和使用视频数据时有效地管理资源和提供高质量的视觉内容。
相关文章:

什么是视频的编码和解码
这段描述中,视频解码能力和视频编码能力指的是不同的处理过程。视频解码是将压缩过的视频数据解开并还原为可播放的视频流,而视频编码是将原始视频数据压缩成更小的尺寸,以减少存储空间和传输带宽。在这个上下文中,解码能力和编码…...

LeetCode 2681. Power of Heroes【排序,数学,贡献法】2060
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
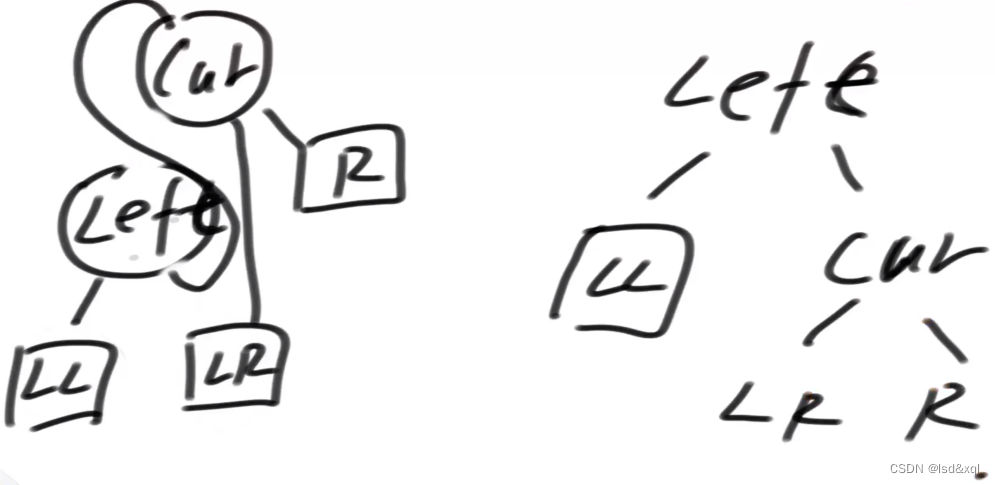
AVL树的讲解
算法拾遗三十八AVL树 AVL树AVL树平衡性AVL树加入节点AVL删除节点AVL树代码 AVL树 AVL树具有最严苛的平衡性,(增、删、改、查)时间复杂度为O(logN),AVL树任何一个节点,左树的高度和右树的高度差…...

Unity 之 Input类
文章目录 总述具体介绍 总述 Input 类是 Unity 中用于处理用户输入的重要工具,它允许您获取来自键盘、鼠标、触摸屏和控制器等设备的输入数据。通过 Input 类,您可以轻松地检测按键、鼠标点击、鼠标移动、触摸、控制器按钮等用户输入事件。以下是关于 I…...
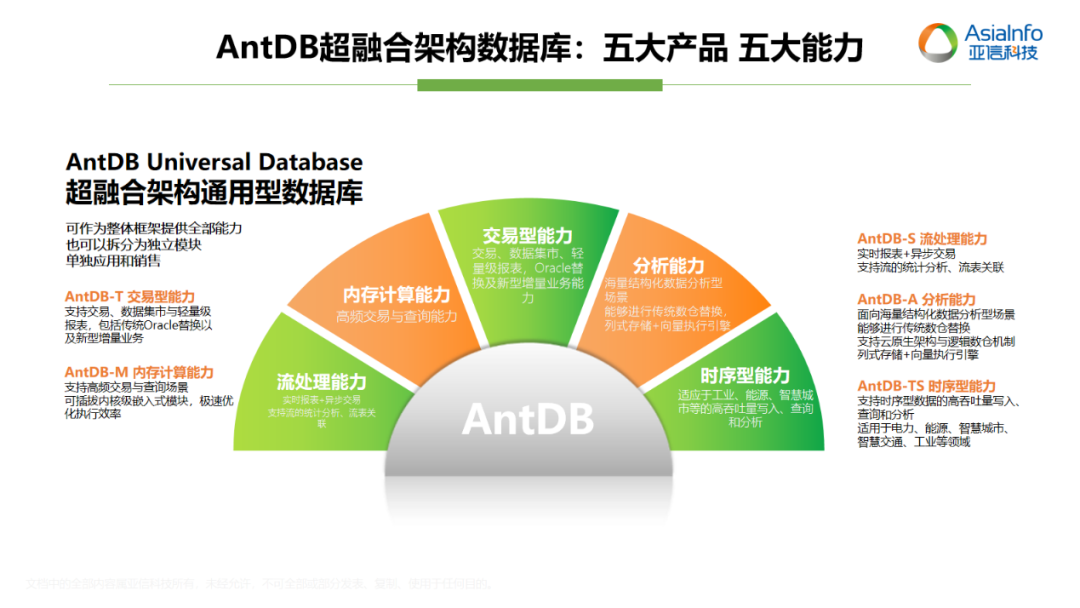
亚信科技AntDB数据库连年入选《中国DBMS市场指南》代表厂商
近日,全球权威ICT研究与顾问咨询公司Gartner发布了2023年《Market Guide for DBMS, China》(即“中国DBMS市场指南”),该指南从市场份额、技术创新、研发投入等维度对DBMS供应商进行了调研。亚信科技是领先的数智化全栈能力提供商…...
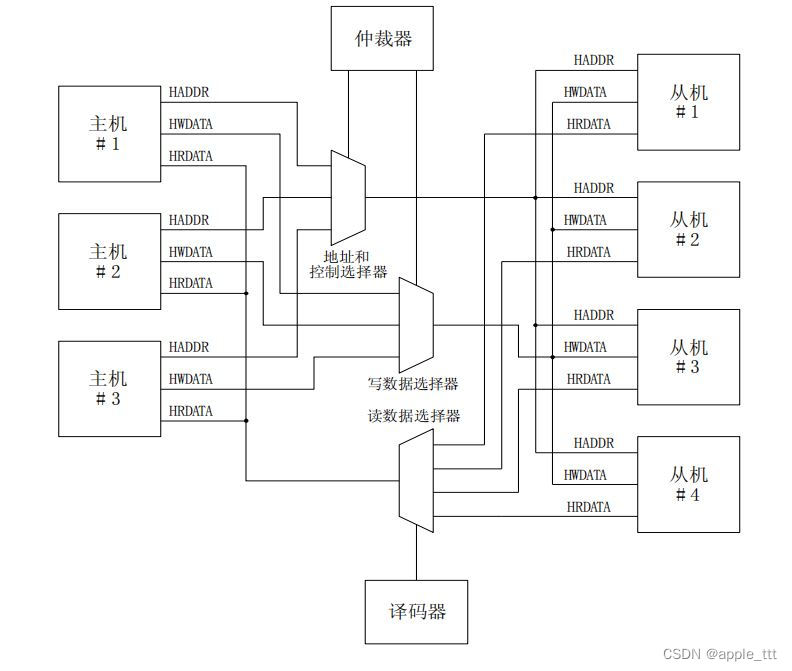
AMBA总线协议(3)——AHB(一)
目录 一、前言 二、什么是AHB总线 1、概述 2、一个典型的基于AHB总线的微处理器架构 3、基本的 AHB 传送特性 三、AMBA AHB总线互联 四、小结 一、前言 在之前的文章中我们初步的了解了一下AMBA总线中AHB,APB,AXI的信号线及其功能,从本文开始我们…...

Git commit与pull的先后顺序
Git commit与pull的先后顺序_git先pull再commit_Mordor Java Girl的博客-CSDN博客 编辑yucoang2020.04.21 回复 28 先pull再commit的话, 你的commit也就不再纯粹了. 这一个commit不再是"你所编辑的xxx功能, 而是"别人所编辑的你所编辑的xxx". 我认为提交历…...
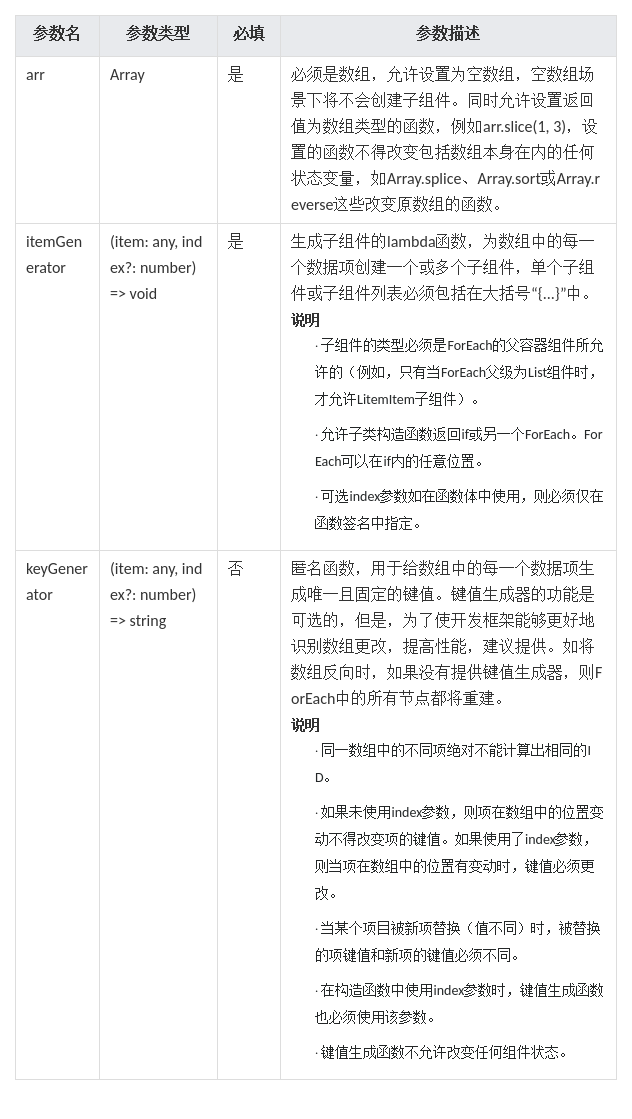
HarmonyOS/OpenHarmony应用开发-ArkTS语言渲染控制ForEach循环渲染
ForEach基于数组类型数据执行循环渲染。说明,从API version 9开始,该接口支持在ArkTS卡片中使用。 一、接口描述 ForEach(arr: any[], itemGenerator: (item: any, index?: number) > void,keyGenerator?: (item: any, index?: number) > stri…...

Powered by Paraverse | 平行云助力彼真科技打造演出“新物种”
01 怎么看待虚拟演出 彼真科技 我们怎么看待虚拟演出? 虚拟演出给音乐人或者音乐行业带来了哪些新的机会?通过呈现一场高标准的虚拟演出,我们的能力延伸点在哪里? 先说一下我们认知里的虚拟演出的本质: 音乐演出是一…...
企微配置回调服务
1、企微配置可信域名 2、企微获取成员userID 3、企微获取用户敏感数据 4、企微配置回调服务 文章目录 一、简介1、概述2、相关文档地址 二、企微配置消息服务器1、配置消息接收参数2、参数解析3、参数拼接规则 三、代码编写—使用已有库1、代码下载2、代码修改3、服务代码编写 …...

机器人远程控制软件设计
机器人远程控制软件设计 That’s all....
:React中的虚拟DOM是什么?)
面试题-React(二):React中的虚拟DOM是什么?
一、什么是虚拟DOM? 虚拟DOM是React的核心概念之一,它是一个轻量级的JavaScript对象树,用于表示真实DOM的状态。在React中,当数据发生变化时,首先会在虚拟DOM上执行DOM更新,而不是直接操作真实DOM。然后&a…...

分布式链路追踪——Dapper, a Large-Scale Distributed Systems Tracing Infrastructure
要解决的问题 如何记录请求经过多个分布式服务的信息,以便分析问题所在?如何保证这些信息得到完整的追踪?如何尽可能不影响服务性能? 追踪 当用户请求到达前端A,将会发送rpc请求给中间层B、C;B可以立刻作…...

【IEEE会议】第二届IEEE云计算、大数据应用与软件工程国际学术会议 (CBASE2023)
第二届IEEE云计算、大数据应用与软件工程国际学术会议 (CBASE2023) 随着大数据时代的到来,对数据获取的随时性和对计算的需求也在逐渐增长。为推动大数据时代的云计算与软件工程的发展,促进该领域学术交流,在CBASE 2022成功举办的…...

Streamlit项目:基于讯飞星火认知大模型开发Web智能对话应用
文章目录 1 前言2 API获取3 官方文档的调用代码4 Streamlit 网页的搭建4.1 代码及效果展示4.2 Streamlit相关知识点 5 结语 1 前言 科大讯飞公司于2023年8月15日发布了讯飞认知大模型V2.0,这是一款集跨领域知识和语言理解能力于一体的新一代认知智能大模型。前日&a…...
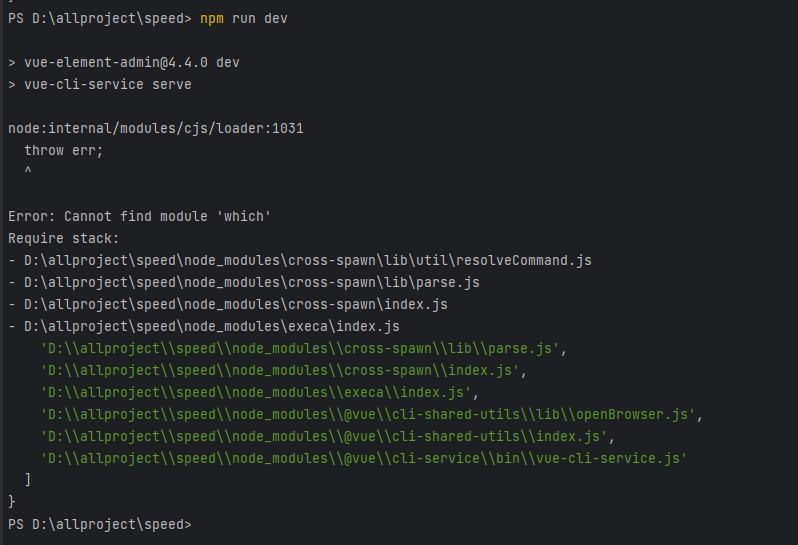
[Vue]解决npm run dev报错node:internal/modules/cjs/loader:1031 throw err;
解决: 有2中方法,建议先尝试第一种,不行再第二种 第一种: 重新安装依赖环境 删除项目的node_modules文件夹,重新执行 # 安装依赖环境 npm install# 运行 npm run dev 我只用了第一种方法就可以了 ,第二种方法从别的博主那看到…...
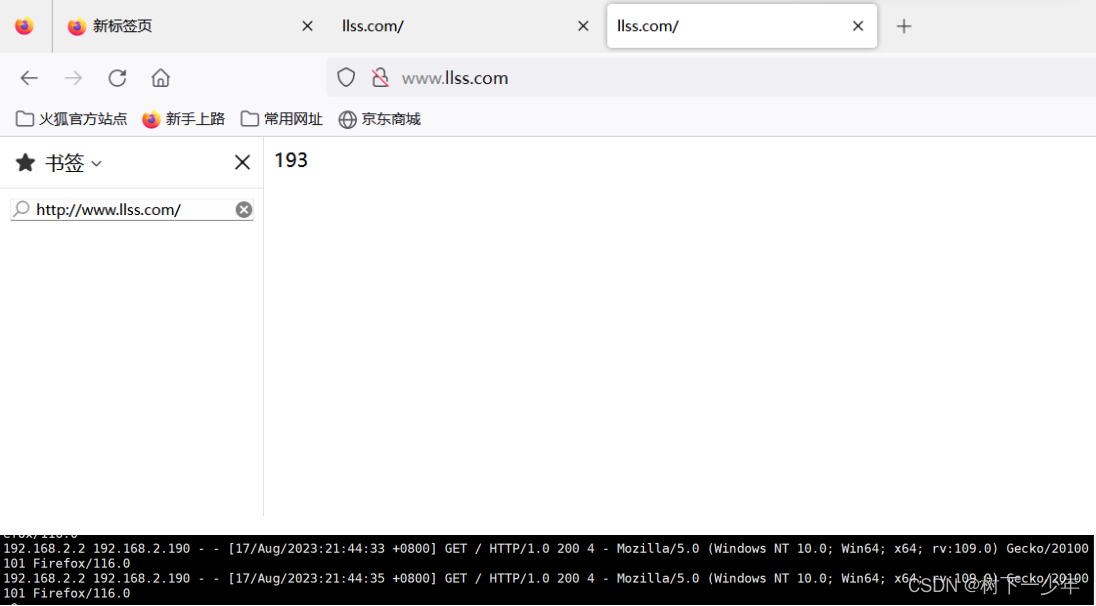
nginx反向代理后实现nginx和apache两种web服务器能够记录客户端的真实IP地址
一.构建环境 二.配置反向代理 1.基于源码安装的nginx环境下修改nginx.conf(设备1) 2.通过windows powershell进行修改hosts文件并测试 3.设备2和设备3上查看日志,可以看到访问来源都是代理服务器(2.190)而不是真实…...
【仿写tomcat】四、解析http请求信息,响应给前端,HttpServletRequest、HttpServletResponse的简单实现
思考 在解析请求之前我们要思考一个问题,我们解析的是其中的哪些内容? 对于最基本的实现,当然是请求类型,请求的url以及请求参数,我们可以根据请求的类型作出对应的处理,通过url在我们的mapstore中找到se…...

FL Studio21.1中文完整版Win/Mac
FL Studio All Plugins Edition【中文完整版 Win/Mac】适合音乐制作人/工作室使用,全套插件!(20.9新增Vintage Chorus,Pitch Shifter变调插件)FL Studio是超多顶级音乐人的启蒙首选!包括百大DJ冠军Martin Garrix&…...
基于Mysql+Vue+Django的协同过滤和内容推荐算法的智能音乐推荐系统——深度学习算法应用(含全部工程源码)+数据集
目录 前言总体设计系统整体结构图系统流程图 运行环境Python 环境MySQL环境VUE环境 模块实现1. 数据请求和储存2. 数据处理计算歌曲、歌手、用户相似度计算用户推荐集 3. 数据存储与后台4. 数据展示 系统测试工程源代码下载其它资料下载 前言 本项目以丰富的网易云音乐数据为基…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
