策略梯度方法
策略梯度方法
数学背景
给定一个标量函数 J ( θ ) J\left(\theta\right) J(θ),利用梯度上升法,使其最大化,此时的 π θ \pi_\theta πθ就是最优策略。
θ t + 1 = θ t + α ∇ θ J ( θ t ) \theta_{t+1}=\theta_t+\alpha \nabla_\theta J(\theta_t) θt+1=θt+α∇θJ(θt)
标量函数 J ( θ ) J(\theta) J(θ)
就是上面提到的最优指标 J J J,一般有以下几种定义:
-
平均状态价值
v ˉ π = ∑ s ∈ S d π ( s ) v π ( s ) = E [ v π ( S ) ] \bar v_\pi =\sum_{s\in\mathcal{S}}d_\pi(s)v_\pi(s) =\mathbb{E}\left[ v_\pi(S) \right] vˉπ=s∈S∑dπ(s)vπ(s)=E[vπ(S)]
如果 d d d与 π \pi π无关,那么记 d π = d 0 d_\pi=d_0 dπ=d0,就Grid World问题,由于状态价值 v v v是回报的期望,考虑两种具体情况:- 起始在随机位置,均匀考虑每个状态价值: d 0 = 1 / ∣ S ∣ d_0=1/|\mathcal{S}| d0=1/∣S∣
- 起始在固定位置,只考虑 s 0 s_0 s0状态价值即可: d 0 ( s 0 ) = 1 , d 0 ( s ≠ s 0 ) d_0(s_0)=1,\ d_0(s\neq s_0) d0(s0)=1, d0(s=s0)
如果 d d d与 π \pi π有关,求解 d π T P π = d π T d_\pi^TP_\pi=d_\pi^T dπTPπ=dπT得到 d π d_\pi dπ,其中 P π P_\pi Pπ是在策略 π \pi π下的状态转移矩阵。此时,如果一个状态经常出现,对应的 d ( s ) d(s) d(s)就会变大。
-
平均瞬时奖励
r ˉ π = ∑ s ∈ S d π ( s ) r π ( s ) = E [ r π ( S ) ] \bar r_\pi=\sum_{s\in \mathcal{S}}d_\pi(s)r_\pi(s)=\mathbb{E}\left[r_\pi(S)\right] rˉπ=s∈S∑dπ(s)rπ(s)=E[rπ(S)]其中 r π ( s ) r_\pi(s) rπ(s)是agent在某状态按策略 π \pi π在动作空间中采取动作的瞬时奖励
r π ( s ) = ∑ a ∈ A π ( s ∣ a ) r ( s , a ) r_\pi(s)=\sum_{a\in \mathcal{A}}\pi(s\mid a)r(s,a) rπ(s)=a∈A∑π(s∣a)r(s,a)此定义与episode reward等价,即当episode长度无限大时, s s s按 d π d_\pi dπ分布,即
lim n → ∞ 1 n E [ ∑ k = 1 n R t + k ] ⟺ r ˉ π \lim_{n\to\infty}\frac{1}{n}\mathbb{E}[\sum_{k=1}^{n}R_{t+k}] \iff \bar r_\pi n→∞limn1E[k=1∑nRt+k]⟺rˉπ
J ( θ ) J(\theta) J(θ)的梯度
上面两类指标函数的梯度都可以写成:
∇ θ J ( θ ) = ∑ s ∈ S η ( s ) ∑ a ∈ A ∇ θ π ( a ∣ s , θ ) q π ( s , a ) = ∑ s ∈ S η ( s ) ∑ a ∈ A π ( a ∣ s , θ ) ∇ θ log π ( a ∣ s , θ ) q π ( s , a ) = E [ ∇ θ log π ( A ∣ S , θ ) q π ( S , A ) ] \begin{aligned} \nabla_\theta J(\theta) &=\sum_{s\in \mathcal{S}}\eta(s)\sum_{a\in \mathcal{A}} \nabla_\theta \pi(a|s,\theta)q_\pi(s,a)\\ &=\sum_{s\in \mathcal{S}}\eta(s)\sum_{a\in \mathcal{A}} \pi(a|s,\theta)\nabla_\theta \log\pi(a|s,\theta)q_\pi(s,a)\\ &=\mathbb{E}[\nabla_\theta \log\pi(A|S,\theta)q_\pi(S,A)] \end{aligned} ∇θJ(θ)=s∈S∑η(s)a∈A∑∇θπ(a∣s,θ)qπ(s,a)=s∈S∑η(s)a∈A∑π(a∣s,θ)∇θlogπ(a∣s,θ)qπ(s,a)=E[∇θlogπ(A∣S,θ)qπ(S,A)]
其中, S ∼ η S\sim \eta S∼η, A ∼ π ( a ∣ s , θ ) A\sim \pi(a|s,\theta) A∼π(a∣s,θ)
训练时,使用随机近似的梯度:
∇ θ J ≈ ∇ θ log π ( a ∣ s , θ ) q π ( s , a ) \nabla_\theta J\approx\nabla_\theta \log\pi(a|s,\theta)q_\pi(s,a) ∇θJ≈∇θlogπ(a∣s,θ)qπ(s,a)
REINFORCE伪代码

相关文章:

策略梯度方法
策略梯度方法 数学背景 给定一个标量函数 J ( θ ) J\left(\theta\right) J(θ),利用梯度上升法,使其最大化,此时的 π θ \pi_\theta πθ就是最优策略。 θ t 1 θ t α ∇ θ J ( θ t ) \theta_{t1}\theta_t\alpha \nabla_\theta…...

博客系统之单元测试
对博客系统进行单元测试 1、测试查找已存在的用户 测试名称 selectByUsernameTest01 测试源码 //查找用户,存在 Test public void selectByUsernameTest01 () { UserDao userDao new UserDao(); String ret1 userDao.selectByUsername("张三").toStr…...

【ARM v8】如何在ARM上实现x86的rdtsc()函数
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G算力网络技术标准研究。 博客…...

redis--事务
redis事务 在Redis中,事务是一组原子性操作的集合,它们被一起执行,要么全部执行成功,要么全部回滚。虽然Redis的事务并不遵循传统数据库的ACID特性,但它仍然提供了一种将多个命令打包成一组执行的机制,适用…...

111. 二叉树的最小深度
111. 二叉树的最小深度 给定一个二叉树,找出其最小深度。 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 说明:叶子节点是指没有子节点的节点。 /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeN…...

SpringMVC归纳与总结
前言 Spring的核心是IOC,一种依赖反转的解耦思想。MVC是一种处理Web请求的架构模式,当两者的作用结合,就形成了SpringMVC。 组成及运行原理 1. 两次映射 2. 为什么用适配器模式 过滤器与拦截器 1. 范围 静态资源与动态资源2. 生命周期…...
_django知识(二))
Python学习笔记_进阶篇(三)_django知识(二)
本章内容 Django model Model 基础配置 django默认支持sqlite,mysql, oracle,postgresql数据库。 <1> sqlite django默认使用sqlite的数据库,默认自带sqlite的数据库驱动 引擎名称:django.db.backends.sqlite3 <2>mysql …...

RISC-V 整型通用寄存器介绍
简介 RISC-V64位/32位提供了32个整型通用寄存器,编号是x0~x31,这些整型通用寄存器的宽度与架构位数一致。 浮点数寄存器与整形寄存器一样也提供了32个:f0~f31,位数与架构位数一致。 通用寄存器介绍 零寄存器 x0/zero x0寄存…...

学习Vue:【性能优化】异步组件和懒加载
在Vue.js应用开发中,性能优化是一个至关重要的主题,而异步组件和懒加载是提升性能的有效方法之一。本文将介绍什么是异步组件和懒加载,以及如何在Vue.js中应用这些技术来提升应用性能。 异步组件和懒加载 异步组件 异步组件是指在需要的时候…...

pdf格式文件下载不预览,云存储的跨域解决
需求背景 后端接口中返回的是pdf文件路径比如: pdf文件路径 (https://wangzhendongsky.oss-cn-beijing.aliyuncs.com/wzd-test.pdf) 前端适配是这样的 <ahref"https://wangzhendongsky.oss-cn-beijing.aliyuncs.com/wzd-test.pdf&…...

httplib + nlohmann::json上传数据时中文乱码解决
1、nlohmann::json 1.1 编码格式使用UTF-8 参考 nlohmann::json 中文乱码解决方案 (1)将数据先转为UTF-8格式 2、httplib 2.1 上传数据前 (1)调用httplib::Response对象的set_header()方法来设置编码格式 httplib::Response res…...

JavaScript中的设计模式之一--单例模式和模块
虽然有一种疯狂天才的感觉可能很诱人,但重新发明轮子通常不是设计软件的最佳方法。很有可能有人已经遇到了和你一样的问题,并以一种聪明的方式解决了它。这样的最佳实践在形式化后被称为设计模式。今天我们来看看它们的概念,并检查单例模式和…...

回归预测 | MATLAB实现GAM广义加性模型多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现GAM广义加性模型多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现GAM广义加性模型多输入单输出回归预测(多指标,多图)效果一览基本介绍程序设计参考资料 效果一览 基本…...

css学习4(背景)
1、CSS中,颜色值通常以以下方式定义: 十六进制 - 如:"#ff0000"RGB - 如:"rgb(255,0,0)"颜色名称 - 如:"red" 2、background-image 属性描述了元素的背景图像. 默认情况下,背景图像进…...
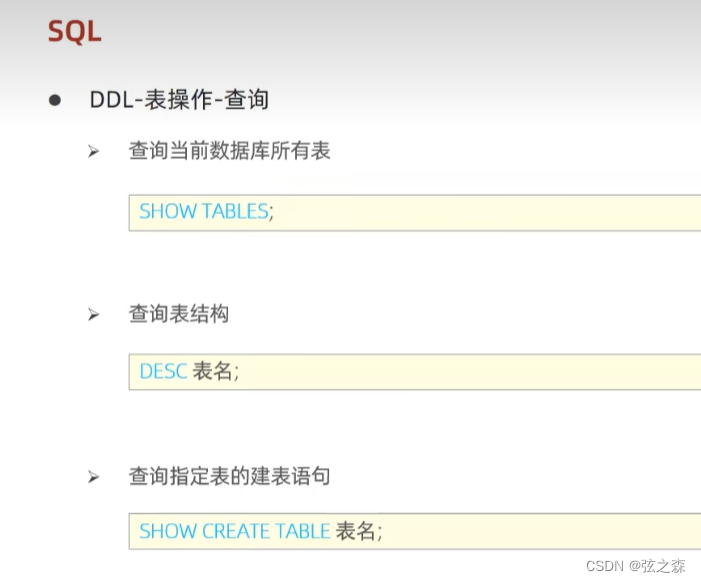
二、SQL,如何实现表的创建和查询
1、新建表格(在当前数据库中新建一个表格): (1)基础语法: create table [表名]( [字段:列标签] [该列数据类型] comment [字段注释], [字段:列标签] [该列数据类型] comment [字段注释], ……,…...

大数据及软件教学与实验专业实训室建设方案
一 、系统概述 大数据及软件教学与实验大数据及软件教学与实验在现代教育中扮演重要角色,这方面的教学内容涵盖了大数据处理、数据分析、数据可视化和大数据应用等多个方面。以下是大数据及软件教学与实验的一般内容:1. 数据基础知识:教授学生…...

信创办公–基于WPS的EXCEL最佳实践系列 (公式和函数)
信创办公–基于WPS的EXCEL最佳实践系列 (公式和函数) 目录 应用背景相关知识操作步骤1、认识基本的初级函数2、相对引用,绝对引用,混合引用3、统计函数4、文本函数 应用背景 熟练掌握Excel的函数工具能让我们在日常的使用中更加方…...
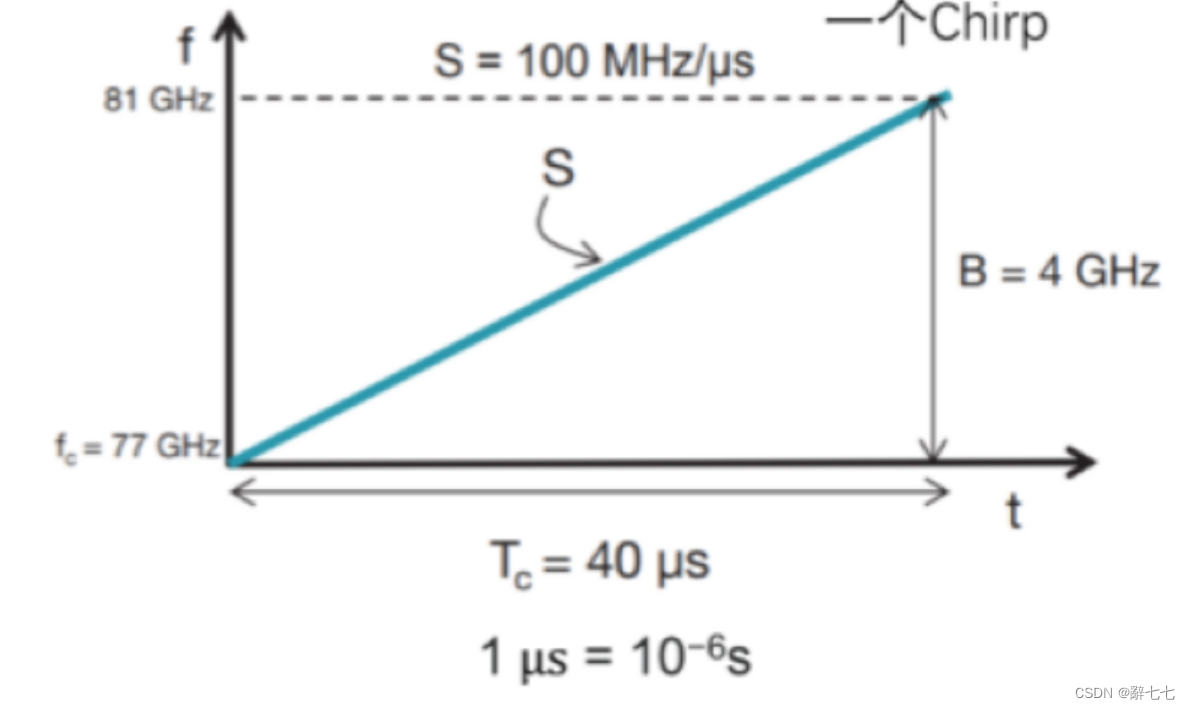
【Apollo】自动驾驶感知——毫米波雷达
作者简介: 辭七七,目前大一,正在学习C/C,Java,Python等 作者主页: 七七的个人主页 文章收录专栏: 七七的闲谈 欢迎大家点赞 👍 收藏 ⭐ 加关注哦!💖…...
SpringBoot部署到腾讯云
SpringBoot部署到腾讯云 此处默认已经申请到腾讯云服务器,因为本人还没有申请域名,所以就直接使用的ip地址 XShell连接到腾讯云 主机中填写腾讯云的公网ip地址 公网ip地址在下图中找到 接下来填写服务器的用户名与密码 一般centOS用户名为rootÿ…...

Git 设置代理
Git 传输分两种协议,SSH和 http(s),设置代理也需要分两种。 http(s) 代理 Command Line 使用 命令行 模式,可以在Powershell中使用以下命令设置代理: $env:http_proxy"http://127.0.0.1:7890" $env:https_proxy&quo…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
