代码随想录训练营day17|110.平衡二叉树 257. 二叉树的所有路径 404.左叶子之和 v...
@TOC
前言
代码随想录算法训练营day17
一、Leetcode 110.平衡二叉树
1.题目
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:true
示例 2:
输入:root = [1,2,2,3,3,null,null,4,4] 输出:false
示例 3:
输入:root = [] 输出:true
提示:
树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/balanced-binary-tree
2.解题思路
解题思路
方法一:自顶向下的递归
定义函数 heightheight,用于计算二叉树中的任意一个节点 pp 的高度:
height(p)={0p 是空节点max(height(p.left),height(p.right))+1p 是非空节点height(p)={0max(height(p.left),height(p.right))+1p 是空节点p 是非空节点
有了计算节点高度的函数,即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历,即对于当前遍历到的节点,首先计算左右子树的高度,如果左右子树的高度差是否不超过 11,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。
3.代码实现
```java class Solution { public boolean isBalanced(TreeNode root) { if (root == null) { return true; } else { return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right); } }
public int height(TreeNode root) {if (root == null) {return 0;} else {return Math.max(height(root.left), height(root.right)) + 1;}
}}
```
二、Leetcode 257. 二叉树的所有路径
1.题目
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]
示例 2:
输入:root = [1] 输出:["1"]
提示:
树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/binary-tree-paths
2.解题思路
方法一:深度优先搜索
思路与算法
最直观的方法是使用深度优先搜索。在深度优先搜索遍历二叉树时,我们需要考虑当前的节点以及它的孩子节点。
如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。
如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。如此,当遍历完整棵二叉树以后我们就得到了所有从根节点到叶子节点的路径。当然,深度优先搜索也可以使用非递归的方式实现,这里不再赘述。
3.代码实现
```java class Solution { public List binaryTreePaths(TreeNode root) { List paths = new ArrayList(); constructPaths(root, "", paths); return paths; }
public void constructPaths(TreeNode root, String path, List<String> paths) {if (root != null) {StringBuffer pathSB = new StringBuffer(path);pathSB.append(Integer.toString(root.val));if (root.left == null && root.right == null) { // 当前节点是叶子节点paths.add(pathSB.toString()); // 把路径加入到答案中} else {pathSB.append("->"); // 当前节点不是叶子节点,继续递归遍历constructPaths(root.left, pathSB.toString(), paths);constructPaths(root.right, pathSB.toString(), paths);}}
}}
```
三、Leetcode 404.左叶子之和 v
1.题目
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1] 输出: 0
提示:
节点数在 [1, 1000] 范围内
-1000 <= Node.val <= 1000来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/sum-of-left-leaves
2.解题思路
方法一:深度优先搜索
3.代码实现
```java class Solution { public int sumOfLeftLeaves(TreeNode root) { return root != null ? dfs(root) : 0; }
public int dfs(TreeNode node) {int ans = 0;if (node.left != null) {ans += isLeafNode(node.left) ? node.left.val : dfs(node.left);}if (node.right != null && !isLeafNode(node.right)) {ans += dfs(node.right);}return ans;
}public boolean isLeafNode(TreeNode node) {return node.left == null && node.right == null;
}}
```
相关文章:

代码随想录训练营day17|110.平衡二叉树 257. 二叉树的所有路径 404.左叶子之和 v...
TOC 前言 代码随想录算法训练营day17 一、Leetcode 110.平衡二叉树 1.题目 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为: 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 示例 1&#x…...

C# Thread用法
C# 中的线程(Thread)是一种并发执行的机制,允许同时执行多个代码块,从而提高程序的性能和响应性。下面是关于如何使用 C# 线程的一些基本用法: 1. 创建线程: 使用 System.Threading 命名空间中的 Thread 类…...
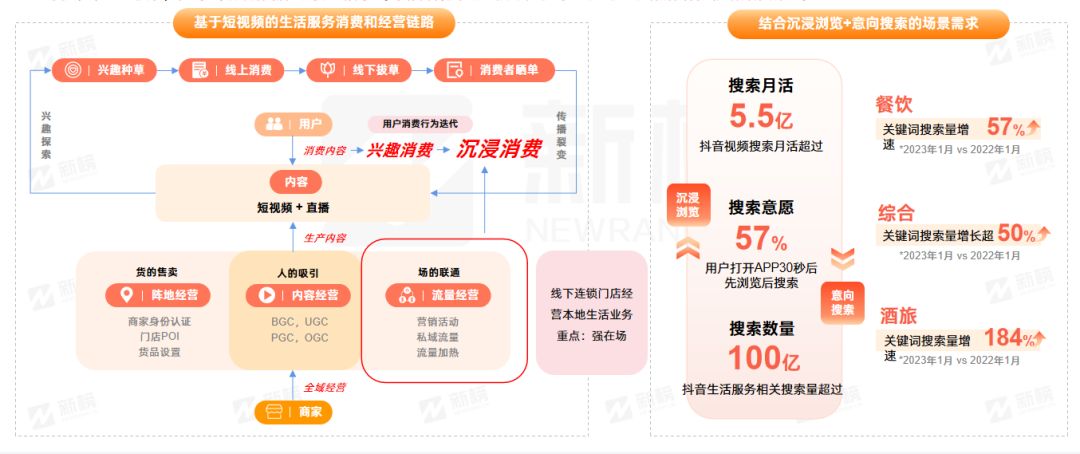
新榜 | CityWalk本地生活商业价值洞察报告
如果说现在有人问,最新的网络热词是什么? “CityWalk”,这可能是大多数人的答案。 近段时间,“CityWalk”刷屏了各种社交媒体,给网友们带来了一场“城市漫步”之旅。 脱离群体狂欢,这个在社交媒体引发热议的词汇背后又…...
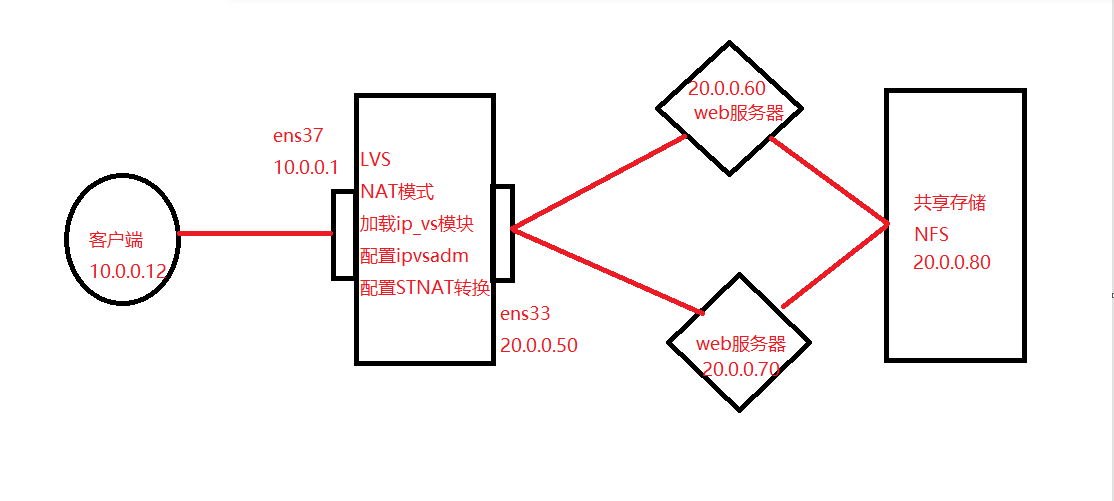
LVS负载均衡集群-NAT模式部署
集群 集群:将多台主机作为一个整体,然后对外提供相同的服务 集群使用场景:高并发的场景 集群的分类 1.负载均衡器集群 减少响应延迟,提高并发处理的能力 2,高可用集群 增强系统的稳定性可靠性&…...

C++学习笔记总结练习:effective 学习日志
准则 1.少使用define define所定义的常量会在预处理的时候被替代,出错编译器不容易找到错误。而且还没有作用范围限制,推荐使用constdefine宏定义的函数,容易出错,而且参数需要加上小括号,推荐使用inline有的类中例如…...

Vue教程(五):样式绑定——class和style
1、样式代码准备 样式提前准备 <style>.basic{width: 400px;height: 100px;border: 1px solid black;}.happy{border: 4px solid red;background-color: rgba(255, 255, 0, 0.644);background: linear-gradient(30deg, yellow, pink, orange, yellow);}.sad{border: 4px …...
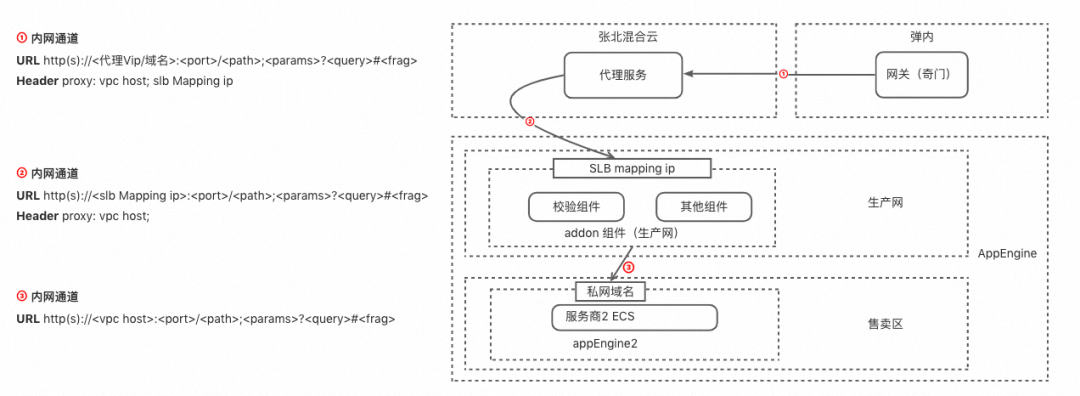
开放网关架构演进
作者:庄文弘(弘智) 淘宝开放平台是阿里与外部生态互联互通的重要开放途径,通过开放的产品技术把阿里经济体一系列基础服务,像水、电、煤一样输送给我们的商家、开发者、社区媒体以及其他合作伙伴,推动行业的…...

torch一些操作
Pytorch文档 Pytorch 官方文档 https://pytorch.org/docs/stable/index.html pytorch 里的一些基础tensor操作讲的不错 https://blog.csdn.net/abc13526222160/category_8614343.html 关于pytorch的Broadcast,合并与分割,数学运算,属性统计以及高阶操作 https://blog.csd…...
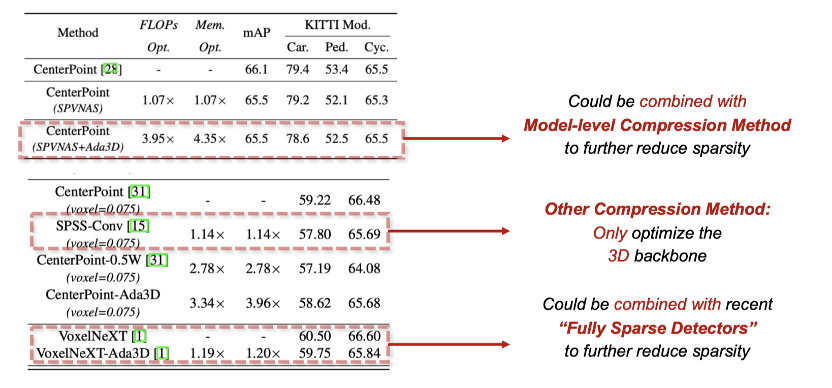
ICCV23 | Ada3D:利用动态推理挖掘3D感知任务中数据冗余性
论文地址:https://arxiv.org/abs/2307.08209 项目主页:https://a-suozhang.xyz/ada3d.github.io/ 01. 背景与动因 3D检测(3D Detection)任务是自动驾驶任务中的重要任务。由于自动驾驶任务的安全性至关重要(safety-critic),对感知算法的延…...

软件工程模型-架构师之路(四)
软件工程模型 敏捷开发: 个体和交互 胜过 过程和工具、可以工作的软件 胜过 面面俱到的文件、客户合作胜过合同谈判、响应变化 胜过 循序计划。(适应需求变化,积极响应) 敏捷开发与其他结构化方法区别特点:面向人的…...
ubuntu20.04共享文件夹—— /mnt/hgfs里没有共享文件夹
参考文章:https://blog.csdn.net/Edwinwzy/article/details/129580636 虚拟机启用共享文件夹后,/mnt/hgfs下面为空,使用 vmware-hgfsclient 查看设置的共享文件夹名字也是为空。 解决方法: 1. 重新安装vmware tools. 在菜单…...
Redis中的有序集合及其底层跳表
前言 本文着重介绍Redis中的有序集合的底层实现中的跳表 有序集合 Sorted Set Redis中的Sorted Set 是一个有序的无重复值的集合,他底层是使用压缩列表和跳表实现的,和Java中的HashMap底层数据结构(1.8)链表红黑树异曲同工之妙…...
js 小程序限流函数 return闭包函数执行不了
问题: 调用限流 ,没走闭包的函数: checkBalanceReq() loadsh.js // 限流 const throttle (fn, context, interval) > {console.log(">>>>cmm throttle", context, interval)let canRun…...

【数据结构】堆的初始化——如何初始化一个大根堆?
文章目录 源码是如何插入的?扩容向上调整实现大根堆代码: 源码是如何插入的? 扩容 在扩容的时候,如果容量小于64,那就2倍多2的扩容;如果大于64,那就1.5倍扩容。 还会进行溢出的判断,…...

【韩顺平 零基础30天学会Java】程序流程控制(2days)
day1 程序流程控制:顺序控制、分支控制、循环控制 顺序控制:从上到下逐行地执行,中间没有任何判断和跳转。 Java中定义变量时要采用合法的前向引用。 分支控制if-else:单分支、双分支和多分支。 单分支 import java.util.Scann…...

从入门到精通Python隧道代理的使用与优化
哈喽,Python爬虫小伙伴们!今天我们来聊聊如何从入门到精通地使用和优化Python隧道代理,让我们的爬虫程序更加稳定、高效!今天我们将对使用和优化进行一个简单的梳理,并且会提供相应的代码示例。 1. 什么是隧道代理&…...

19万字智慧城市总体规划与设计方案WORD
导读:原文《19万字智慧城市总体规划与设计方案WORD》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。 感知基础设施 感知基础设施架构由感知范围、感知手…...
[赛博昆仑] 腾讯QQ_PC端,逻辑漏洞导致RCE漏洞
简介 !! 内容仅供学习,请不要进行非法网络活动,网络不是法外之地!! 赛博昆仑是国内一家较为知名的网络安全公司,该公司今日报告称 Windows 版腾讯 QQ 桌面客户端出现高危安全漏洞,据称“黑客利用难度极低、危害较大”,腾讯刚刚已经紧急发布…...
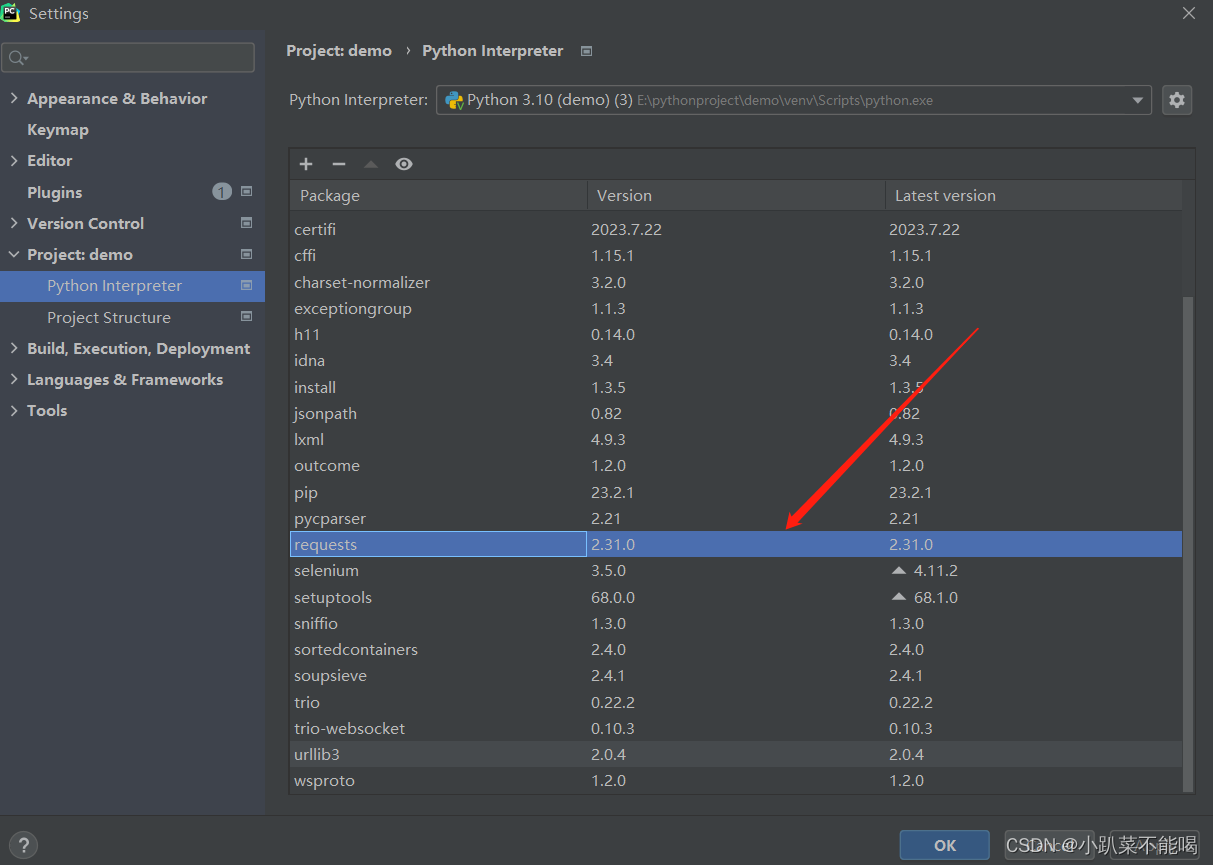
python Requests
Requests概述 官方文档:http://cn.python-requests.org/zh_CN/latest/,Requests是python的HTTP的库,我们可以安全的使用 Requests安装 pip install Requests -i https://pypi.tuna.tsinghua.edu.cn/simple Requests的使用 Respose的属性 属性说明url响…...

【深入解析:数据结构栈的魅力与应用】
本章重点 栈的概念及结构 栈的实现方式 数组实现栈接口 栈面试题目 概念选择题 一、栈的概念及结构 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端 称为栈顶,另一端称为栈底。栈中的数…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
