神经网络基础-神经网络补充概念-42-梯度检验
概念
梯度检验(Gradient Checking)是一种验证数值计算梯度与解析计算梯度之间是否一致的技术,通常用于确保实现的反向传播算法正确性。在深度学习中,通过梯度检验可以帮助验证你的神经网络模型是否正确地计算了梯度,从而减少可能的错误。
梯度检验的基本思想是使用数值近似来估计梯度,然后将数值梯度与解析梯度进行比较,如果它们之间非常接近,那么可以认为反向传播算法的实现是正确的。这是一个在调试和验证模型实现时常用的技术。
代码实现
假设你有一个简单的函数 f(x) = x^2,并且你想计算在某个点 x 处的梯度。
def forward_propagation(x):return x ** 2def backward_propagation(x):return 2 * xdef gradient_check(x, epsilon=1e-7):analytical_gradient = backward_propagation(x)# 计算数值梯度x_plus_epsilon = x + epsilonx_minus_epsilon = x - epsilonnumerical_gradient = (forward_propagation(x_plus_epsilon) - forward_propagation(x_minus_epsilon)) / (2 * epsilon)# 比较数值梯度和解析梯度diff = abs(analytical_gradient - numerical_gradient)if diff < epsilon:print("Gradient check passed!")else:print("Gradient check failed!")x = 2.0
gradient_check(x)相关文章:

神经网络基础-神经网络补充概念-42-梯度检验
概念 梯度检验(Gradient Checking)是一种验证数值计算梯度与解析计算梯度之间是否一致的技术,通常用于确保实现的反向传播算法正确性。在深度学习中,通过梯度检验可以帮助验证你的神经网络模型是否正确地计算了梯度,从…...
<kernel>kernel 6.4 USB-之-hub_port_connect()分析
<kernel>kernel 6.4 USB-之-hub_port_connect()分析 kernel 6.4 USB系列文章如下: <kernel>kernel 6.4 USB-之-hub_event()分析 <kernel>kernel 6.4 USB-之-port_event()分析 <kern…...
linux驱动学习3-外部中断
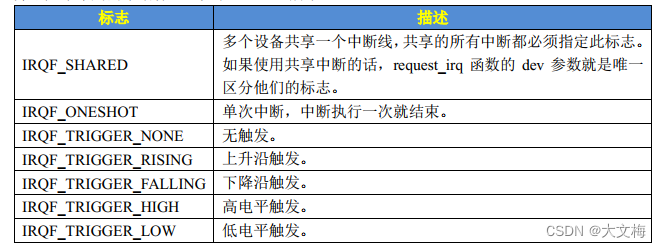
在做中断试验时,发现中断驱动总是insmod失败,之后定位到 gpio_request 失败,之后是想到使用的野火做好的系统,在uEnv.txt中会加载大量设备树插件,将key相关的设备树插件屏蔽即可。 linux中断API函数 中断号 每个中断…...

vue中的canvas插件
vue中canvas插件有vue-konva、vue-fabricjs、vue-canvas-effect、vue-chartjs和vue-threejs等。详细介绍:1、vue-konva是一个用于在Vue.js中使用Konva.js的插件,Konva.js是一个功能强大的HTML5 2D 渲染引擎,可以用于创建交互式的Canvas应用程…...
分享图片 | 快速浏览网页资源,批量保存、一键分享图片
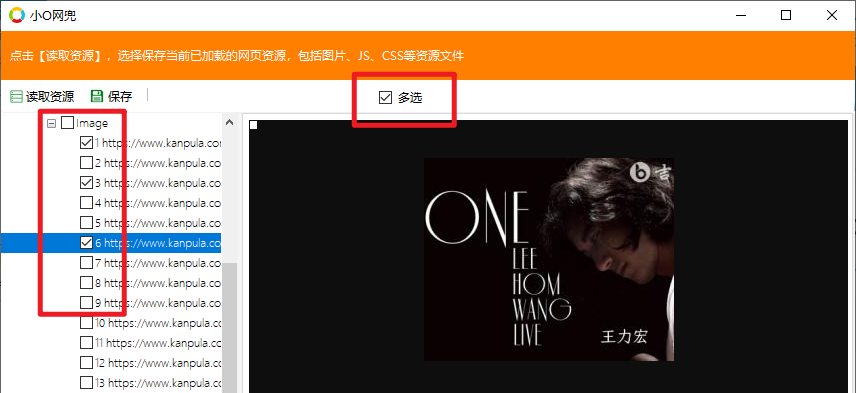
前言 小伙伴学习吉他,有时需要在互联网搜索曲谱资源,而多数曲谱均为图片,并且为多页,在电脑上显示练习很不方便,需要停下来点击鼠标进行翻页,影响练习的连贯性。 为了解决上述问题,通常把图片…...

Programming abstractions in C阅读笔记:p123-p126
《Programming Abstractions In C》学习第50天,p123-p126,总结如下: 一、技术总结 1.notaion 这也是一个在计算机相关书籍中出现的词,但有时却不是那么好理解,因为它可以指代很多对象,这里做一个记录。示…...
-[通用功能:LLMChain、RouterChain和SequentialChain])
自然语言处理从入门到应用——LangChain:链(Chains)-[通用功能:LLMChain、RouterChain和SequentialChain]
分类目录:《自然语言处理从入门到应用》总目录 LLMChain LLMChain是查询LLM对象最流行的方式之一。它使用提供的输入键值(如果有的话,还包括内存键值)格式化提示模板,将格式化的字符串传递给LLM,并返回LLM…...
ElasticSearch-安装部署全过程
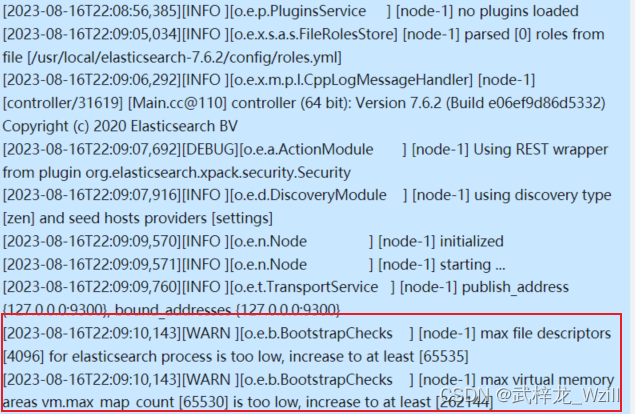
本文已收录于专栏 《中间件合集》 目录 概念说明什么是ElasticSearch什么是Kibana什么是RESTful API 提供服务安装过程安装ElasticSearch1.下载ElasticSearch 安装包2.解压安装包3.进入解压之后的文件夹4.创建一个data文件夹用来存储数据5.进入config文件夹编辑elasticsearch.y…...

mathematica报错:Tag Plus is \ Protected
在使用化简函数Simplify的时候使用了规则的语法,但是规则可能没有使用等号。 例如 Simplify[(1 - c^2)/d^2, c^2 d^2 1]等号被认为是赋值符号,要修改为两个等号: Simplify[(1 - c^2)/d^2, c^2 d^2 1]这样就不会报错了。...
Python Django 模型概述与应用
今天来为大家介绍 Django 框架的模型部分,模型是真实数据的简单明确的描述,它包含了储存的数据所必要的字段和行为,Django 遵循 DRY Principle 。它的目标是你只需要定义数据模型,然后其它的杂七杂八代码你都不用关心,…...
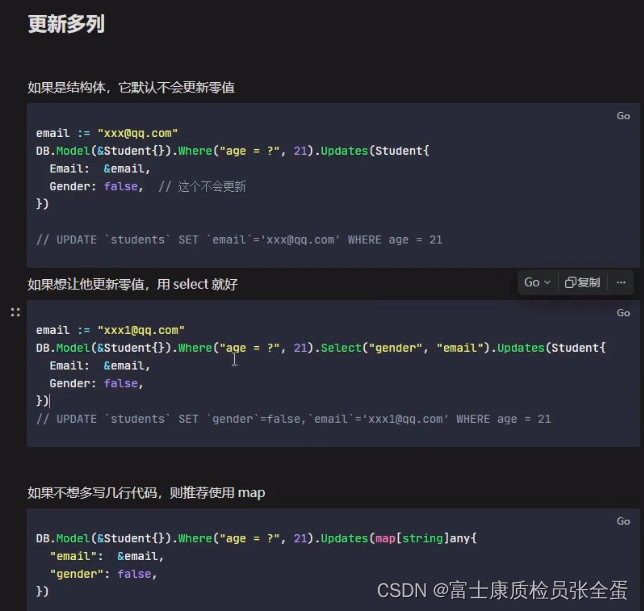
Golang Gorm 更新字段 save update updates
更新和删除操作的前提条件都是要在找到数据的情况下,先要查询到数据才可以做操作。 更新的前提的先查询到记录,Save保存所有字段,用于单个记录的全字段更新它会保控所有字段,即使零值也会保存。 在更新和删除之前,要利…...

springBoot 配置文件引入 redis 的相关参数说明
在Spring Boot应用中使用Redis作为缓存或数据存储时,可以在应用的配置文件中配置相关参数。下面是常用的Redis配置参数及其说明: spring.redis.host: Redis服务器主机地址,默认为localhost。spring.redis.port: Redis服务器端口,…...

Docker的使用心得:简化开发与部署的利器
开发与测试的无缝衔接: Docker让开发与测试之间的切换变得前所未有的顺畅。我可以在本地开发环境中创建一个与生产环境一致的Docker容器,这样不仅可以确保开发过程中不会出现意外问题,还可以在测试阶段避免不必要的繁琐配置。 跨平台的可移植…...

vue3 基于element plus对el-pagination进行二次封装
vue3 基于element plus对el-pagination进行二次封装 1、前言2、在components文件夹中新建pagination.vue文件3、在组件内使用分页 1、前言 在vue3项目中,如果每个列表页都敲一遍分页方法,显然是不合理的,那么,下面我将基于elemen…...

RuntimeError: result type Float can‘t be cast to the desired output type __int64报错解决方法
小白刚开始学习YOLOv5,跟随老哥的步骤走了一遍目标检测--手把手教你搭建自己的YOLOv5目标检测平台 最后训练最后一步出现RuntimeError: result type Float can‘t be cast to the desired output type __int64报错 解决方法:找到5.0版报错的loss.py中最…...

解析Python爬虫常见异常及处理方法
作为专业爬虫程序猿长期混迹于爬虫ip解决方案中,我们经常会遇到各种各样的异常情况。在爬虫开发过程中,处理这些异常是不可或缺的一部分。本文将为大家总结常见的Python爬虫异常,并分享相应的处理方法,帮助你避免绊倒在爬虫之路上…...
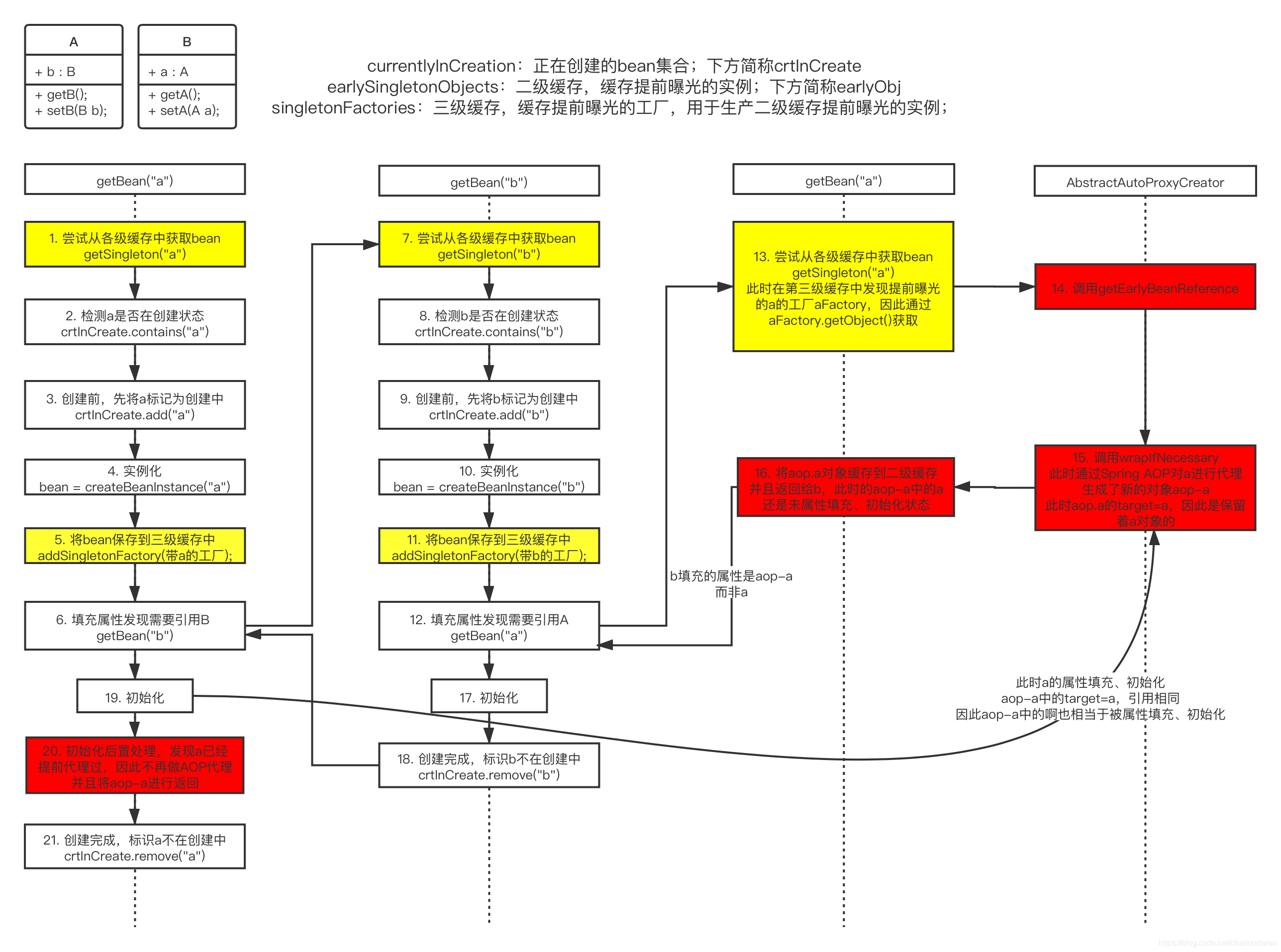
详解Spring的循环依赖问题、三级缓存解决方案源码分析
0、基础:Bean的生命周期 在Spring中,由于IOC的控制反转,创建对象不再是简单的new出来,而是交给Spring去创建,会经历一系列Bean的生命周期才创建出相应的对象。而循环依赖问题也是由Bean的生命周期过程导致的问题&#…...

oracle分析函数学习
0、建表及插入测试数据 --CREATE TEST TABLE AND INSERT TEST DATA. create table students (id number(15,0), area varchar2(10), stu_type varchar2(2), score number(20,2));insert into students values(1, 111, g, 80 ); insert into students values(1, 111, j, 80 ); …...

代码随想录训练营day17|110.平衡二叉树 257. 二叉树的所有路径 404.左叶子之和 v...
TOC 前言 代码随想录算法训练营day17 一、Leetcode 110.平衡二叉树 1.题目 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为: 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 示例 1&#x…...

C# Thread用法
C# 中的线程(Thread)是一种并发执行的机制,允许同时执行多个代码块,从而提高程序的性能和响应性。下面是关于如何使用 C# 线程的一些基本用法: 1. 创建线程: 使用 System.Threading 命名空间中的 Thread 类…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
