当前位置： 首页 > news >正文

[Go版]算法通关村第十三关白银——数组实现加法和幂运算

news 2025/10/31 20:23:41

目录

  • 数组实现加法专题
    • 题目：数组实现整数加法
      • 思路分析：
      • 复杂度：
      • Go代码
    • 题目：字符串加法
      • 思路分析：
      • 复杂度：
      • Go代码
    • 题目：二进制加法
      • 思路分析：
      • 复杂度：
      • Go代码
  • 幂运算专题
    • 题目：求2的幂
      • 思路分析：
      • 复杂度：
      • Go代码
    • 题目：求3的幂
      • 思路分析：
      • 复杂度：
      • Go代码
    • 题目：求4的幂
      • 思路分析：
      • 复杂度：
      • Go代码

数组实现加法专题

题目：数组实现整数加法

思路分析：

复杂度：

Go代码

在这里插入代码片

题目：字符串加法

思路分析：

复杂度：

Go代码

在这里插入代码片

题目：二进制加法

思路分析：

复杂度：

Go代码

在这里插入代码片

幂运算专题

题目：求2的幂

思路分析：

复杂度：

Go代码

在这里插入代码片

题目：求3的幂

思路分析：

复杂度：

Go代码

在这里插入代码片

题目：求4的幂

思路分析：

复杂度：

Go代码

在这里插入代码片

相关文章：

[Go版]算法通关村第十三关白银——数组实现加法和幂运算

目录 数组实现加法专题题目：数组实现整数加法思路分析：复杂度：Go代码 题目：字符串加法思路分析：复杂度：Go代码 题目：二进制加法思路分析：复杂度：Go代码 幂运算专题题目&a…...

编程日记 2023/8/22 11:01:37

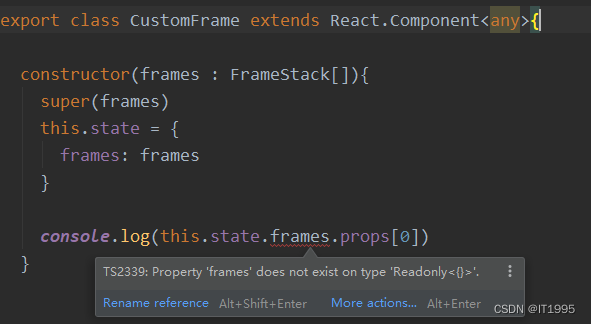
React笔记[tsx]-解决Property ‘frames‘ does not exist on type ‘Readonly＜{}＞‘

浏览器报错如下&#xff1a; 编辑器是这样的&#xff1a; 原因是React.Component<any>少了后面的any&#xff0c;改成这样即可&#xff1a; export class CustomFrame extends React.Component<any, any>{............ }...

编程日记 2023/8/22 11:00:35

ThinkPHP6.0+ 使用Redis 原始用法

composer 安装 predis/predis 依赖&#xff0c;或者安装php_redis.dll的扩展。 我这里选择的是predis/predis 依赖。 composer require predis/predis 进入config/cache.php 配置添加redis缓存支持 示例&#xff1a; <?php// -----------------------------------------…...

编程日记 2023/8/22 10:59:34

SRM系统询价竞价管理：优化采购流程的全面解析

SRM系统的询价竞价管理模块是现代企业采购管理中的重要工具。通过该模块&#xff0c;企业可以实现供应商的询价、竞价和合同管理等关键环节的自动化和优化。 一、概述 SRM系统是一种用于管理和优化供应商关系的软件系统。它通过集成各个环节&#xff0c;包括供应商信息管理、询…...

编程日记 2023/8/22 10:58:32

c++选择题笔记

局部变量能否和全局变量重名&#xff1f;可以&#xff0c;局部变量会屏蔽全局变量。在使用全局变量时需要使用 ":: "。拷贝构造函数&#xff1a;参数为同类型的对象的常量引用的构造函数函数指针&#xff1a;int (*f)(int,int) & max; 虚函数&#xff1a;在基类…...

编程日记 2023/8/22 10:57:31

Android2:构建交互式应用

一。创建项目 项目名Beer Adviser 二。更新布局 activity_main.xml <?xml version"1.0" encoding"utf-8"?><LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"…...

编程日记 2023/8/22 10:56:28

ChatGLM-6B微调记录

目录 GLM-130B和ChatGLM-6BChatGLM-6B直接部署基于PEFT的LoRA微调ChatGLM-6B GLM-130B和ChatGLM-6B 对于三类主要预训练框架&#xff1a; autoregressive&#xff08;无条件生成&#xff09;&#xff0c;GPT的训练目标是从左到右的文本生成。autoencoding&#xff08;语言理解…...

编程日记 2023/8/22 10:55:27

Linux Kernel 4.12 或将新增优化分析工具

到 7 月初&#xff0c;Linux Kernel 4.12 预计将为修复所有安全漏洞而奠定基础&#xff0c;另外新增的是一个分析工具&#xff0c;对于开发者优化启动时间时会有所帮助。 新的「个别任务统一模型」&#xff08;Per-Task Consistency Model&#xff09;为主要核心实时修补&#…...

编程日记 2023/8/22 10:54:26

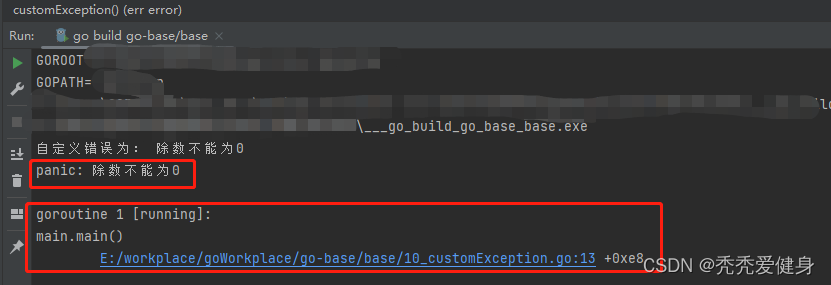
【30天熟悉Go语言】10 Go异常处理机制

作者&#xff1a;秃秃爱健身&#xff0c;多平台博客专家&#xff0c;某大厂后端开发&#xff0c;个人IP起于源码分析文章 &#x1f60b;。 源码系列专栏&#xff1a;Spring MVC源码系列、Spring Boot源码系列、SpringCloud源码系列&#xff08;含&#xff1a;Ribbon、Feign&…...

编程日记 2023/8/22 10:53:25

飞机打方块（四）游戏结束

一、游戏结束显示 1.新建节点 1.新建gameover节点 2.绑定canvas 3.新建gameover容器 4.新建文本节点 2.游戏结束逻辑 Barrier.ts update(dt: number) {//将自身生命值取整let num Math.floor(this.num);//在Label上显示this.num_lb.string num.toString();//获取GameCo…...

编程日记 2023/8/22 10:52:23

保研之旅1：西北工业大学电子信息学院夏令营

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; 本人持续分享更多关于电子通信专业内容以及嵌入式和单片机的知识&#xff0c;如果大家喜欢&#xff0c;别忘点个赞加个关注哦&#xff0c;让我们一起共同进步~ &#x…...

编程日记 2023/8/22 10:51:20

[WMCTF 2023] crypto

似乎退步不了&#xff0c;这个比赛基本不会了&#xff0c;就作了两个简单题。 SIGNIN 第1个是签到题 from Crypto.Util.number import * from random import randrange from secret import flagdef pr(msg):print(msg)pr(br"""........ …...

编程日记 2023/8/22 10:50:19

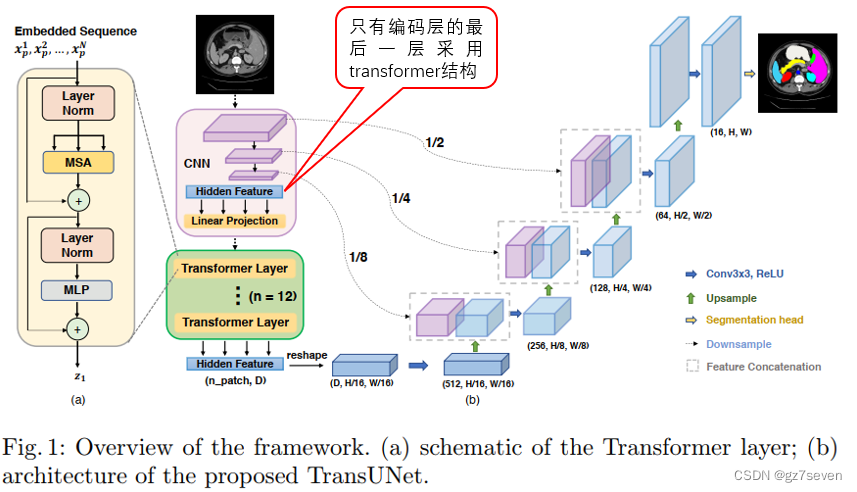
图像分割unet系列------TransUnet详解

图像分割unet系列------TransUnet详解 1、TransUnet结构2、我关心的问题3、总结与展望TransUnet发表于2021年，它是对UNet非常重要的改进，专为医学图像分割任务设计，特别用于在医学图像中分割器官或病变等解剖结构。 1、TransUnet结构 TransUNet在U-Net模型的基础上引入了混合…...

编程日记 2023/8/22 10:49:17

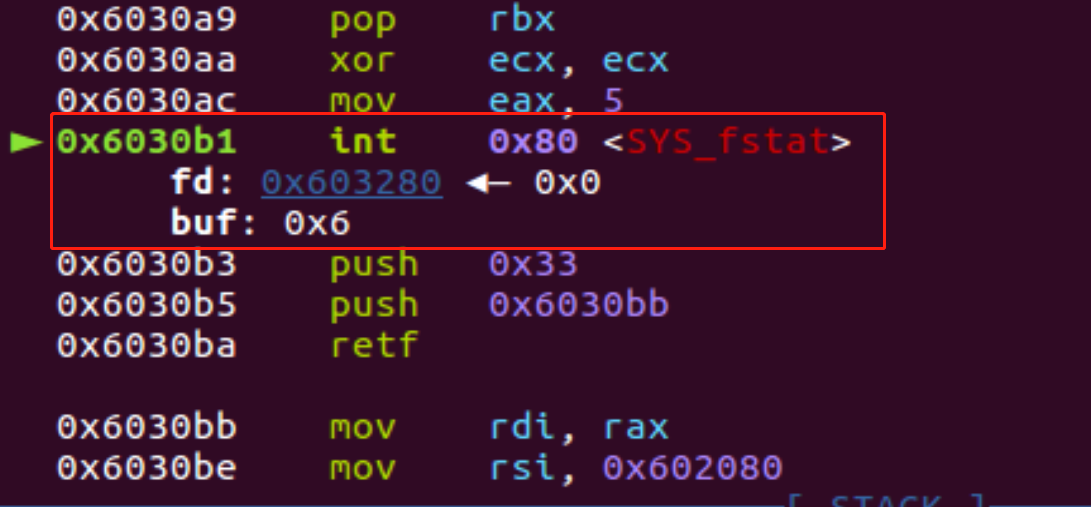
ASCII码-shellcode的技巧

网上已经有成熟的工具了&#xff0c;所以就简单记录一下工具怎么用吧 https://github.com/TaQini/alpha3 https://github.com/veritas501/ae64.git https://github.com/rcx/shellcode_encoder 结合题目来看吧&#xff0c;没有开启NX保护&#xff0c;基本这类型题目九成九都…...

编程日记 2023/8/22 10:48:16

spring cloud 之 dubbo nacos整合

整体思路&#xff1a; 搭建本地nacos服务&#xff0c;详见docker安装nacos_xgjj68163的博客-CSDN博客 共三个工程&#xff0c;生产者服务、消费者服务、生产者和消费者共同依赖的接口工程&#xff08;打成jar&#xff0c;供生产者和消费者依赖&#xff09;&#xff1b; …...

编程日记 2023/8/22 10:47:15

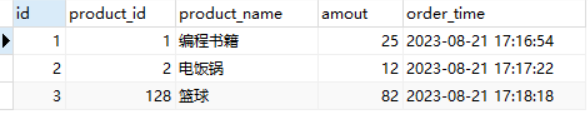
MySQL如何进行表之间的关联更新

在实际编程工作或运维实践中&#xff0c;对MySQL数据库表进行关联更新是一种比较常见的应用场景&#xff0c;比如在电商系统中&#xff0c;订单表里保存了商品名称的信息&#xff08;冗余字段设计&#xff09;&#xff0c;但如果商品名称发生变化&#xff0c;则需要通过关联商品…...

编程日记 2023/8/22 10:46:13

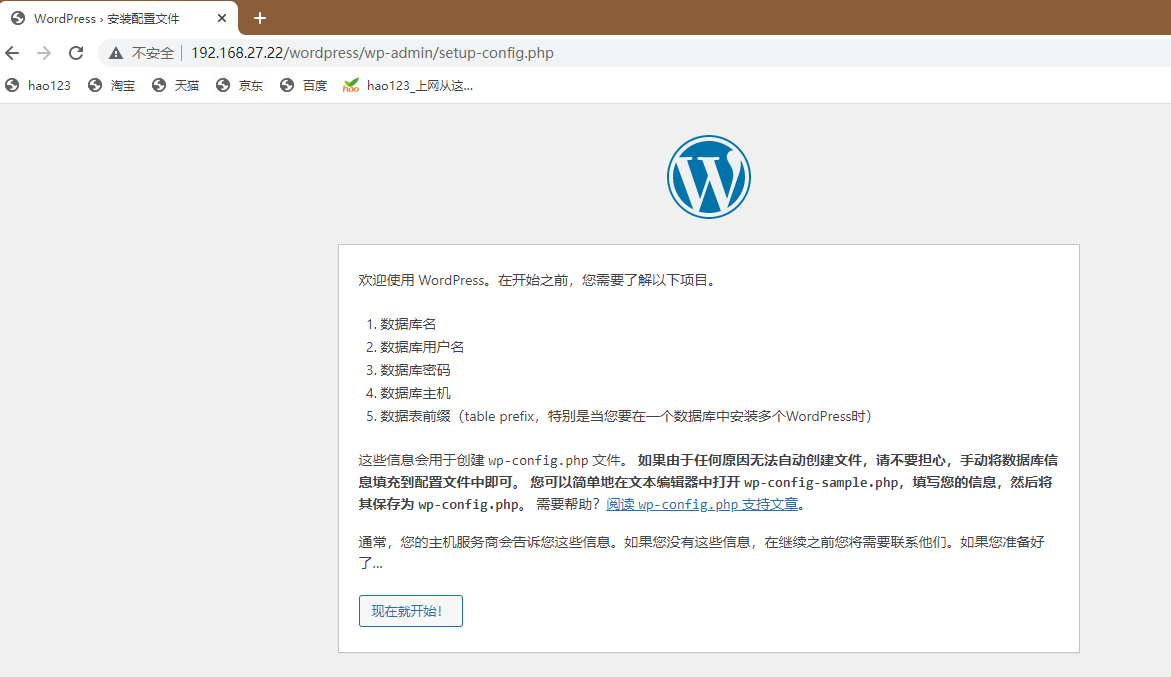
Docker创建 LNMP 服务+Wordpress 网站平台

Docker创建 LNMP 服务Wordpress 网站平台 一.环境及准备工作 1.项目环境 公司在实际的生产环境中&#xff0c;需要使用 Docker 技术在一台主机上创建 LNMP 服务并运行 Wordpress 网站平台。然后对此服务进行相关的性能调优和管理工作。 容器 系统 IP地址 软件 nginx centos…...

编程日记 2023/8/22 10:45:11

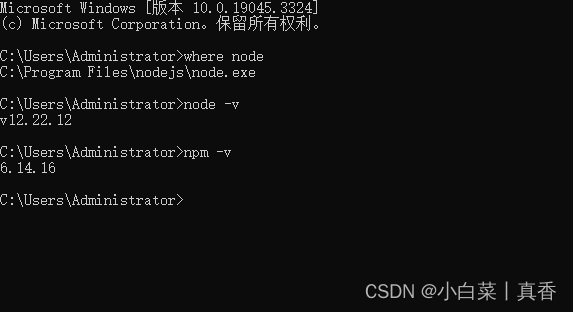
node没有自动安装npm时，如何手动安装 npm

之前写过一篇使用 nvm 管理 node 版本的文章&#xff0c;node版本管理&#xff08;Windows&#xff09; 有时候&#xff0c;我们使用 nvm 下载 node 时&#xff0c;node 没有自动下载 npm &#xff0c;此时就需要我们自己手动下载 npm 1、下载 npm下载地址&#xff1a;&…...

编程日记 2023/8/22 10:44:10

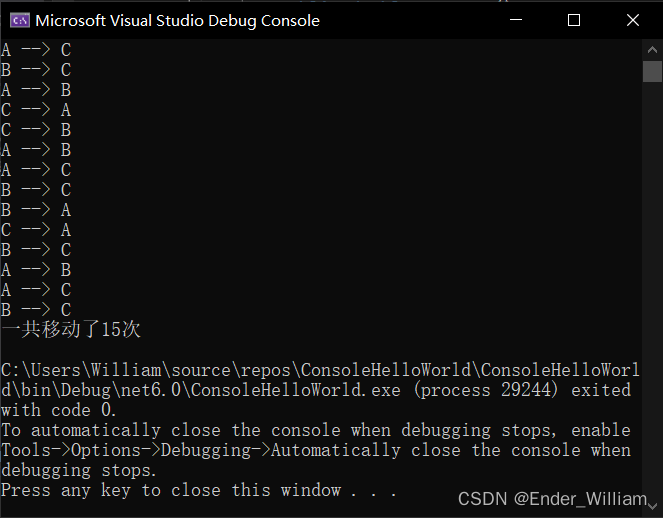
C# 使用递归方法实现汉诺塔步数计算

C# 使用递归方法实现汉诺塔步数计算 Part 1 什么是递归Part 2 汉诺塔Part 3 程序 Part 1 什么是递归 举一个例子&#xff1a;计算从 1 到 x 的总和 public int SumFrom1ToX(int x) {if(x 1){return 1;}else{int result x SumFrom1ToX_2(x - 1); // 调用自己return result…...

编程日记 2023/8/22 10:43:09

窗口函数大揭秘！轻松计算数据累计占比，玩转数据分析的绝佳利器

上一篇文章《如何用窗口函数实现排名计算》中小编为大家介绍了窗口函数在排名计算场景中的应用&#xff0c;但实际上窗口函数除了可以进行单行计算&#xff0c;还可以在每行上打开一个指定大小的计算窗口&#xff0c;这个计算窗口可以由SQL中的语句具体指定&#xff0c;大到整个…...

编程日记 2023/8/22 10:42:08

多云管理“拦路虎”：深入解析网络互联、身份同步与成本可视化的技术复杂度​

一、引言&#xff1a;多云环境的技术复杂性本质​​ 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时&#xff0c;​​基础设施的技术债呈现指数级积累​​。网络连接、身份认证、成本管理这三大核心挑战相互嵌套&#xff1a;跨云网络构建数据…...

编程新知 2025/10/31 17:16:18

idea大量爆红问题解决

问题描述 在学习和工作中&#xff0c;idea是程序员不可缺少的一个工具&#xff0c;但是突然在有些时候就会出现大量爆红的问题&#xff0c;发现无法跳转&#xff0c;无论是关机重启或者是替换root都无法解决 就是如上所展示的问题&#xff0c;但是程序依然可以启动。 问题解决…...

编程新知 2025/10/30 10:46:50

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关

一、模块概述 ngx_stream_return_module 提供了一个极简的指令&#xff1a; return <value>;在收到客户端连接后&#xff0c;立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量&#xff08;如 $time_iso8601、$remote_addr 等&#xff09;&a…...

编程新知 2025/9/21 0:49:02

反向工程与模型迁移：打造未来商品详情API的可持续创新体系

在电商行业蓬勃发展的当下&#xff0c;商品详情API作为连接电商平台与开发者、商家及用户的关键纽带&#xff0c;其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息&#xff08;如名称、价格、库存等&#xff09;的获取与展示&#xff0c;已难以满足市场对个性化、智能…...

编程新知 2025/9/15 5:56:53

【位运算】消失的两个数字（hard）

消失的两个数字&#xff08;hard&#xff09; 题⽬描述&#xff1a;解法&#xff08;位运算&#xff09;&#xff1a;Java 算法代码&#xff1a;更简便代码 题⽬链接&#xff1a;⾯试题 17.19. 消失的两个数字 题⽬描述&#xff1a; 给定⼀个数组&#xff0c;包含从 1 到 N 所有…...

编程新知 2025/10/17 12:01:41

Linux简单的操作

ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

编程新知 2025/9/11 13:56:27

C++ 基础特性深度解析

目录 引言 一、命名空间&#xff08;namespace&#xff09; C 中的命名空间​ 与 C 语言的对比​ 二、缺省参数​ C 中的缺省参数​ 与 C 语言的对比​ 三、引用&#xff08;reference&#xff09;​ C 中的引用​ 与 C 语言的对比​ 四、inline&#xff08;内联函数…...

编程新知 2025/10/17 0:18:22

【Zephyr 系列 10】实战项目：打造一个蓝牙传感器终端 + 网关系统（完整架构与全栈实现）

🧠关键词：Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者：希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数：约 5200 字 ✨ 项目总览 在物联网实际项目中，**“终端 + 网关”**是…...

编程新知 2025/10/27 21:51:36

Rapidio门铃消息FIFO溢出机制

关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系&#xff0c;以下是深入解析&#xff1a; 门铃FIFO溢出的本质 在RapidIO系统中&#xff0c;门铃消息FIFO是硬件控制器内部的缓冲区&#xff0c;用于临时存储接收到的门铃消息&#xff08;Doorbell Message&#xff09;。…...

编程新知 2025/10/30 3:57:10

莫兰迪高级灰总结计划简约商务通用PPT模版

莫兰迪高级灰总结计划简约商务通用PPT模版&#xff0c;莫兰迪调色板清新简约工作汇报PPT模版&#xff0c;莫兰迪时尚风极简设计PPT模版&#xff0c;大学生毕业论文答辩PPT模版&#xff0c;莫兰迪配色总结计划简约商务通用PPT模版&#xff0c;莫兰迪商务汇报PPT模版&#xff0c;…...

编程新知 2025/10/29 1:49:43