[WMCTF 2023] crypto

似乎退步不了,这个比赛基本不会了,就作了两个简单题。
SIGNIN
第1个是签到题
from Crypto.Util.number import *
from random import randrange
from secret import flagdef pr(msg):print(msg)pr(br"""....''''''.... .`",:;;II;II;;;;:,"^'. '"IlllI;;;;;;;;;;;;;Il!!l;^. `l><>!!!!!!!!iiiii!!!!!!!!i><!". ':>?]__++~~~~~<<<<<<<<<<<<<<<<~~+__i". .:i+}{]?-__+++~~~~~~<<<<<~~~~~~+_-?[\1_!^ .;<_}\{]-_++~<<<<<<<<<<<<<<<<<<<~+-?]\|]+<^ .!-{t|[?-}(|((){_<<<<<<<<<_}1)))1}??]{t|]_" !)nf}]-?/\){]]]_<<<<<<<<<_]]}}{\/?-][)vf?` '!tX/}]--<]{\Un[~~<<<<<~~<~-11Yz)<--?[{vv[". .<{xJt}]?!ibm0%&Ci><<<<<<<<!0kJW%w+:-?[{uu)}, !1fLf}]_::xmqQj["I~<<<<<<>"(ZqOu{I^<?[{cc)[` `}|x\}]_+<!<+~<<__~<<<<<<+_<<_+<><++-[1j/(> !\j/{]-++___--_+~~<i;I>~~~__-______?}(jf}` ;~(|}?_++++~~++~+]-++]?+++~~~~+++-[1/]>^ ;\([?__+_-?]?-_-----__-]?-_+++-]{/]. l||}?__/rjffcCQQQQQLUxffjf}+-]1\?' ,[\)[?}}-__[/nzXXvj)?__]{??}((>. .I[|(1{]_+~~~<~~<<<~+_[}1(1+^ ,~{|\)}]_++++++-?}1)1?!` ."!_]{11))1{}]-+i:' .`^","^`'.
""".decode())def gen_prime(bit):while 1:P = getPrime(bit)if len(bin(P)) - 2 == bit:return Ppq_bit = 512
offset = 16P,Q = [gen_prime(pq_bit) for i in range(2)]
N = P * Q
gift = int(bin(P ^ (Q >> offset))[2+offset:],2)
pr(N)
pr(gift)inpP = int(input())
if inpP != P:pr(b"you lose!")exit()secret = randrange(0,P)
bs = [randrange(0,P) for _ in range(38)]results = [(bi * secret) % P for bi in bs]
rs = [ri & (2 ** offset - 1) for ri in results]pr(bs)
pr(rs)
inpsecret = int(input())
if inpsecret == secret:pr(flag)两部分第一部分是个爆破p^(q>>16)
gift = int(bin(P ^ (Q >> offset))[2+offset:],2)第二部分是一个hnp问题,与常见的不同,原来是 B = A*x + b这里给的是A和b求B,这题本来不会,但前天有一个比赛也是这个题,也不会,广大姥要了WP,根据那个WP写一下就行了。
第一部分
from pwn import *io = remote('1.13.101.243', 26140 )
context.log_level = 'debug'for _ in range(24):io.recvline()def fac(x,tp,tq):global p if p != 0:returnif len(x) == 0:returnif tp*tq>N:returnif N%(tp+1)==0:print(tp+1)p = tp+1returnv = x[0]r = x[1:]l = len(r)if (tp+(1<<(l+1)))*(tq+(1<<(l+17)))<N:return if v == '0':fac(r, tp, tq)fac(r, tp+(1<<l), tq+(1<<(l+16)))else:fac(r, tp+(1<<l), tq)fac(r, tp, tq+(1<<(l+16)))N = int(io.recvline())
print(N)
gift = int(io.recvline())
x = bin(gift)[2:].zfill(512-16)
print(x[:50])p = 0
#p前15位未知
for hp in range(1<<15):if hp%0x1000 == 0:print(hex(hp))tp = (1<<511)+ (hp<<512-16-1)if x[0] == '0':tp += 1<<(512-16-1)tq = (1<<(511))fac(x[1:],tp,tq)if p != 0:break io.sendline(str(p).encode())
第二部分
A = eval(io.recvline())
b = eval(io.recvline())
B = 2^16print(f"{p = }")
print(f"{A = }")
print(f"{b = }")sol = int(input('sol='))io.sendline(str(sol).encode())
print(io.recvline())io.interactive()badprime
这是个RSA题,最后才出,难度比较小。
p = k*M + r
可以输入M,给出p%M的值,显然这里只能输入M,然后coppersimth求k
原题
from Crypto.Util.number import *
from secret import flagM = 0x7cda79f57f60a9b65478052f383ad7dadb714b4f4ac069997c7ff23d34d075fca08fdf20f95fbc5f0a981d65c3a3ee7ff74d769da52e948d6b0270dd736ef61fa99a54f80fb22091b055885dc22b9f17562778dfb2aeac87f51de339f71731d207c0af3244d35129feba028a48402247f4ba1d2b6d0755baff6def getMyprime(BIT):while True:p = int(pow(65537, getRandomRange(M>>1, M), M)) + getRandomInteger(BIT-int(M).bit_length()) * Mif isPrime(p):return pp = getMyprime(1024)
q = getPrime(1024)
n = p * q
m = bytes_to_long(flag)print("Try to crack the bad RSA")
print("Public key:", n)
print("The flag(encrypted):", pow(m, 65537, n))
print("Well well, I will give you the hint if you please me ^_^")
leak = int(input("Gift window:"))
if M % leak == 0:print("This is the gift for you: ", p % leak)
else:print("I don't like this gift!")
取数
┌──(kali㉿kali)-[~]
└─$ nc 1.13.101.243 26086
Try to crack the bad RSA
Public key: 9742410937110696461407112349699118236918457640950632920212795068374737936993342570963570443656476362238888124280173501476715660532234383908363410810325565092828457724260500094074310976465439133379654136956954969400177970645885438501653328305955812320073239582404081688376029009382502861319019563066540964659677575484346073160213626650310710260741949702931555358818963239172398313264967023252795746331804500033700165496526109847749240713539566702141086846689655725502183261216470115828779150622670477792032393842776851714610961219730469419362345806447065512890382493060186679828260265857866140764306386881882549166059
The flag(encrypted): 1673402070143155927322001035133684146816738492230807731633827901952184786734541292011662658981062894242325327877506962350481690686305101327856759348839937660438396133590644401938568726337539332758333618463217894304453290225710789062464107920895112595149601246277505775421072733759692860886887303527889771493564848232892813177891652600172884862175447947822901530128111336592984421258891521336361945375551264204284260029356005647086620008139176194080359501299190921098147822016114664277256058464418457390881573150209603439315104193219972739816965833683983804527550309212725954113363913887790377813026135333782360027419
Well well, I will give you the hint if you please me ^_^
Gift window:19467773070115377343221509599623925236459751278180415885837207534756855405403128279156705968461708578168638327032034542684864920135818987044810141311008655898015207220772515212093850725541003213054560185603695585660265284153421684796257245143362498012760214539505870197264858636122745485373430
This is the gift for you: 3919234716983693931577570915609109697211099065875069949073051641072090520857441022482511192871418764059751265895543741460544614322144961090655257474754910444266016317938260233309368531551350066234134348206616531225276790017532193136255605520389973662219840028068705375923569595556552528548183
求值
P.<x> = PolynomialRing(Zmod(n))
f = x*M + M_prime
f.small_roots(X=2^53, beta=0.2, epsilon=0.03)
k = 4429807550221656p = k*M + M_prime
q = n//p
d = inverse_mod(65537, (p-1)*(q-1))
m = pow(c,d,n)
#71802904779908417281632177730640329722234828721755228551576131323789654417934437971480843565056115983321708839293
bytes.fromhex(hex(m)[2:])
#b'wmctf{b4d_primE_f4ctor_1s_the_w3akness_for_RSA}'welconsigner2
这是WP里的,在这里复制保存一下。
两题都是对快速注入错误,求d,第一题一开始给错了,反正不会也就没看。以下是WP原文
对于快速幂的第i步运算,正常情况下已知Ai = Ai-1 * Bi-1^di (mod n);Bi = Bi-1^2 (mod n)
错误注入后,上述式子改为在模数n_下进行计算,此时得到Ai' = Ai-1 * Bi-1^di (mod n_);Bi' = Bi-1^2 (mod n_)
我们以快速幂的最后一次计算为例(错误也注入在最后一次),此时An、An'即为错误注入前、后的RSA签名。此时Bn、Bn'的值都是可以通过计算得到的,通过在模n、n_上分别尝试计算An-1的值我们即可确定dn的值(对于正确的dn值,An、An'倒推出的An-1值应该是相同的)
类似地,在得到An-1与dn的值之后,我们可以将错误注入在倒数第二次,进一步求出An-2与dn-1的值,如此即可利用n次错误注入恢复完整的RSA私钥d
from Crypto.Util.number import *nbits = 512def oracle(index):io.sendlineafter(b'| [Q]uit', b's')io.sendlineafter(b'Where your want to interfere:', str(index).encode())io.recvuntil(b'signature of \"Welcome_come_to_WMCTF\" is ')sig = int(io.recvline().strip())return sigmsg = bytes_to_long(b"Welcome_come_to_WMCTF")
def func(sig, n, e, n_):nn = nbits*2dbit = [0 for _ in range(nn+1)]from tqdm import trangefor i in trange(nn):for now_dbit in range(2):now = dbit[:]now[nn-i] = now_dbitB, B_ = msg, msgN, N_ = n, nres, res_ = 1, 1for j in range(nn):if now[j] == 1:res = res * B % Nres_ = res_ * B_ % N_if j >= nn-1-i:N_ = n_B = B ** 2 % NB_ = B_**2 % N_sig_ = oracle(i)tmp = (sig * inverse(res, N) % N) * res_ % N_if tmp == sig_:dbit = nowbreakelse:raise Exception(f"Failure[{i}]")dbit[0] = 1d = int(''.join(str(_) for _ in dbit)[::-1], 2)print(d)print(pow(233, e*d, n))return dfrom pwn import *
io = remote('1.13.101.243', 26891)io.sendlineafter(b'| [Q]uit', b'g')
io.recvuntil(b'n = ')
n = int(io.recvline().strip())
io.recvuntil(b'flag_ciphertext = ')
ct = bytes.fromhex(io.recvline().strip().decode())sig = oracle(0)io.sendlineafter(b'| [Q]uit', b'f')
io.sendlineafter(b'bytes, and index:', b'255,1')
tmp = 255
index = 1
n_ = n ^ (int(tmp)<<int(index))
e = 17d = func(sig, n, e, n_)
io.close()
from Crypto.Cipher import AES
from hashlib import md5key = bytes.fromhex(md5(str(d).encode()).hexdigest())
enc = AES.new(key, mode=AES.MODE_ECB)
flag = enc.decrypt(ct)
print(flag)
# WMCTF{F4u1t_1nj3ct1on_1n_RS4*&iu2726457}welcomesigner1
第二个的快速幂算法有变化
def myfastexp(m,d,N,j,N_):A = 1d = bin(d)[2:]n = len(d)for i in range(n-1,-1,-1):if i < j:#print(A)N = N_A = A*A % Nif d[i] == "1":A = A * m % Nreturn A
这需要将N_改为一个素数且%4==3然后通过勒让德符号计算,反正特别复杂,看得头大
from Crypto.Util.number import *
from tqdm import trangenbits = 512
m = bytes_to_long(b"Welcome_come_to_WMCTF")def init():while True:# generatep = getPrime(nbits)q = getPrime(nbits)n = p*qe = 17if GCD(e,(p-1)*(q-1)) == 1:d = inverse(e,(p-1)*(q-1))breakwhile True:n_ = next_prime(n)if n_ % 4 == 3:breakprint(f"{n = }\n{n_ = }")return n, e, n_, ddef oracle(index):io.sendlineafter(b'| [Q]uit', b's')io.sendlineafter(b'Where your want to interfere:', str(index).encode())io.recvuntil(b'signature of \"Welcome_come_to_WMCTF\" is ')sig = int(io.recvline().strip())return sigdef func(sig, n, e, n_):def ZZ_sqrt_root(res):R.<x> = ZZ[]return (x^2-ZZ(res)).roots()def GF_sqrt_root(res, p):if pow(res, (p-1)//2, p) == 1:ans = ZZ(pow(res, (p+1)//4, p))return [ans, p-ans]return []nn = 2*nbitsdbits = ''A = sigfor i in trange(1, nn+1):sig_ = oracle(i)As_ = [sig_]for j in dbits:nxt = list()for A_ in As_:if j == '1':nxt += GF_sqrt_root(ZZ(A_*inverse(m, n_)%n_), n_)else:nxt += GF_sqrt_root(ZZ(A_), n_)As_ = [ZZ(_) for _ in nxt]flag = Falsefor j in range(2):for A_ in As_:if j == 1:s = crt([ZZ(A*inverse(m, n)%n),ZZ(A_*inverse(m, n_)%n_)], [n, n_])else:s = crt([A, A_], [n, n_])ans = ZZ_sqrt_root(s)if ans:dbits += str(j)A = max(_[0] for _ in ans)flag = Trueif not flag:raise Exception(f"Error[{i}], {dbits}")ans = int(dbits.rstrip('0')[::-1], 2)print(f"{ans = }")print(pow(233, e*ans, n))return ansfrom pwn import *
host, port = '1.13.101.243:26592'.split(':')
io = remote(host, int(port))
io = process('./server.py')io.sendlineafter(b'| [Q]uit', b'g')
io.recvuntil(b'n = ')
n = int(io.recvline().strip())
io.recvuntil(b'flag_ciphertext = ')
ct = bytes.fromhex(io.recvline().strip().decode())sig = oracle(0)flag = False
for tmp in trange(256):for index in range(1024):n_ = n ^^ (int(tmp)<<int(index))if isPrime(n_) and n_%4 == 3:print(tmp, index)flag = Truebreakif flag:break
io.sendlineafter(b'| [Q]uit', b'f')
io.sendlineafter(b'bytes, and index:', f'{tmp},{index}'.encode())print(f"{ct = }")e = 17
d = func(sig, n, e, n_)
io.close()from Crypto.Cipher import AES
from hashlib import md5key = bytes.fromhex(md5(str(d).encode()).hexdigest())
enc = AES.new(key, mode=AES.MODE_ECB)
flag = enc.decrypt(ct)
print(flag)
# WMCTF{F4u1t_1nj3ct1on_1n_RS4!$%@5!#$128467}相关文章:

[WMCTF 2023] crypto
似乎退步不了,这个比赛基本不会了,就作了两个简单题。 SIGNIN 第1个是签到题 from Crypto.Util.number import * from random import randrange from secret import flagdef pr(msg):print(msg)pr(br"""........ …...
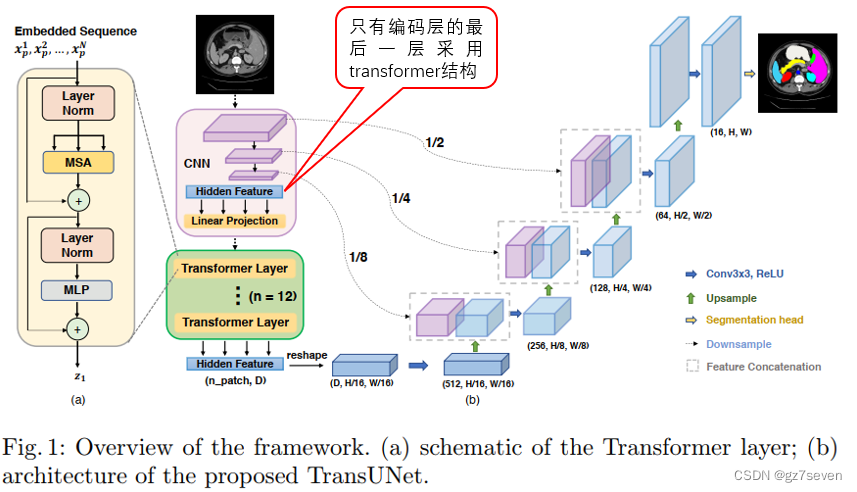
图像分割unet系列------TransUnet详解
图像分割unet系列------TransUnet详解 1、TransUnet结构2、我关心的问题3、总结与展望TransUnet发表于2021年,它是对UNet非常重要的改进,专为医学图像分割任务设计,特别用于在医学图像中分割器官或病变等解剖结构。 1、TransUnet结构 TransUNet在U-Net模型的基础上引入了混合…...
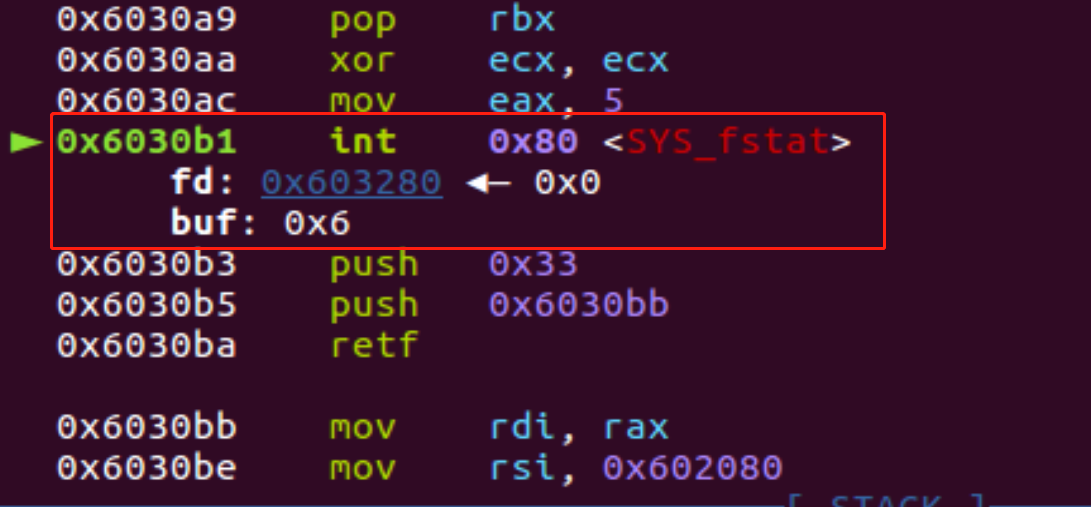
ASCII码-shellcode的技巧
网上已经有成熟的工具了,所以就简单记录一下工具怎么用吧 https://github.com/TaQini/alpha3 https://github.com/veritas501/ae64.git https://github.com/rcx/shellcode_encoder 结合题目来看吧,没有开启NX保护,基本这类型题目九成九都…...

spring cloud 之 dubbo nacos整合
整体思路: 搭建本地nacos服务,详见docker安装nacos_xgjj68163的博客-CSDN博客 共三个工程,生产者服务、消费者服务、生产者和消费者共同依赖的接口工程(打成jar,供生产者和消费者依赖); …...
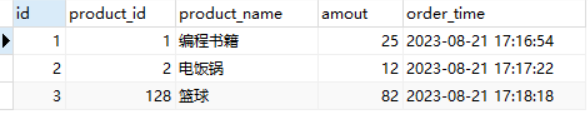
MySQL如何进行表之间的关联更新
在实际编程工作或运维实践中,对MySQL数据库表进行关联更新是一种比较常见的应用场景,比如在电商系统中,订单表里保存了商品名称的信息(冗余字段设计),但如果商品名称发生变化,则需要通过关联商品…...
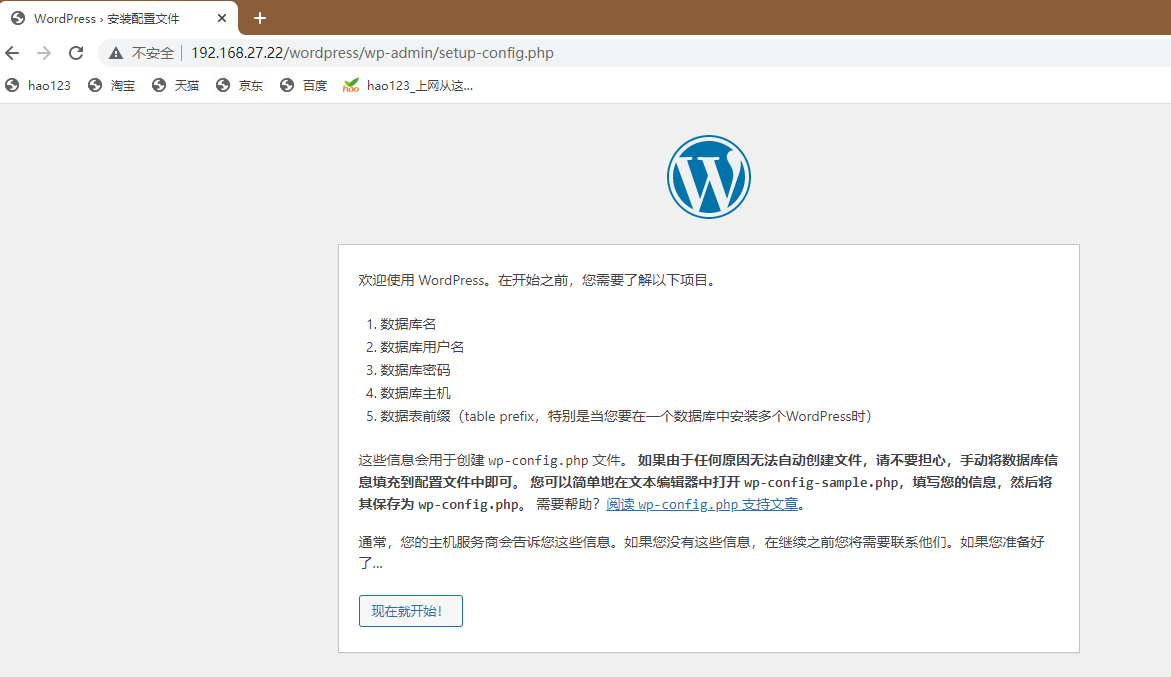
Docker创建 LNMP 服务+Wordpress 网站平台
Docker创建 LNMP 服务Wordpress 网站平台 一.环境及准备工作 1.项目环境 公司在实际的生产环境中,需要使用 Docker 技术在一台主机上创建 LNMP 服务并运行 Wordpress 网站平台。然后对此服务进行相关的性能调优和管理工作。 容器 系统 IP地址 软件 nginx centos…...
node没有自动安装npm时,如何手动安装 npm
之前写过一篇使用 nvm 管理 node 版本的文章,node版本管理(Windows) 有时候,我们使用 nvm 下载 node 时,node 没有自动下载 npm ,此时就需要我们自己手动下载 npm 1、下载 npm下载地址:&…...
C# 使用递归方法实现汉诺塔步数计算
C# 使用递归方法实现汉诺塔步数计算 Part 1 什么是递归Part 2 汉诺塔Part 3 程序 Part 1 什么是递归 举一个例子:计算从 1 到 x 的总和 public int SumFrom1ToX(int x) {if(x 1){return 1;}else{int result x SumFrom1ToX_2(x - 1); // 调用自己return result…...

窗口函数大揭秘!轻松计算数据累计占比,玩转数据分析的绝佳利器
上一篇文章《如何用窗口函数实现排名计算》中小编为大家介绍了窗口函数在排名计算场景中的应用,但实际上窗口函数除了可以进行单行计算,还可以在每行上打开一个指定大小的计算窗口,这个计算窗口可以由SQL中的语句具体指定,大到整个…...

健康检测智能睡眠床垫方案
《2022中国睡眠质量调查报告》调查结果显示,16%的被调查者存在夜间睡眠时间不足6个小时,表现为24点以后才上床睡觉,并且在6点之前起床;有83.81%的被调查者经常受到睡眠问题困扰,其中入睡困难占2…...
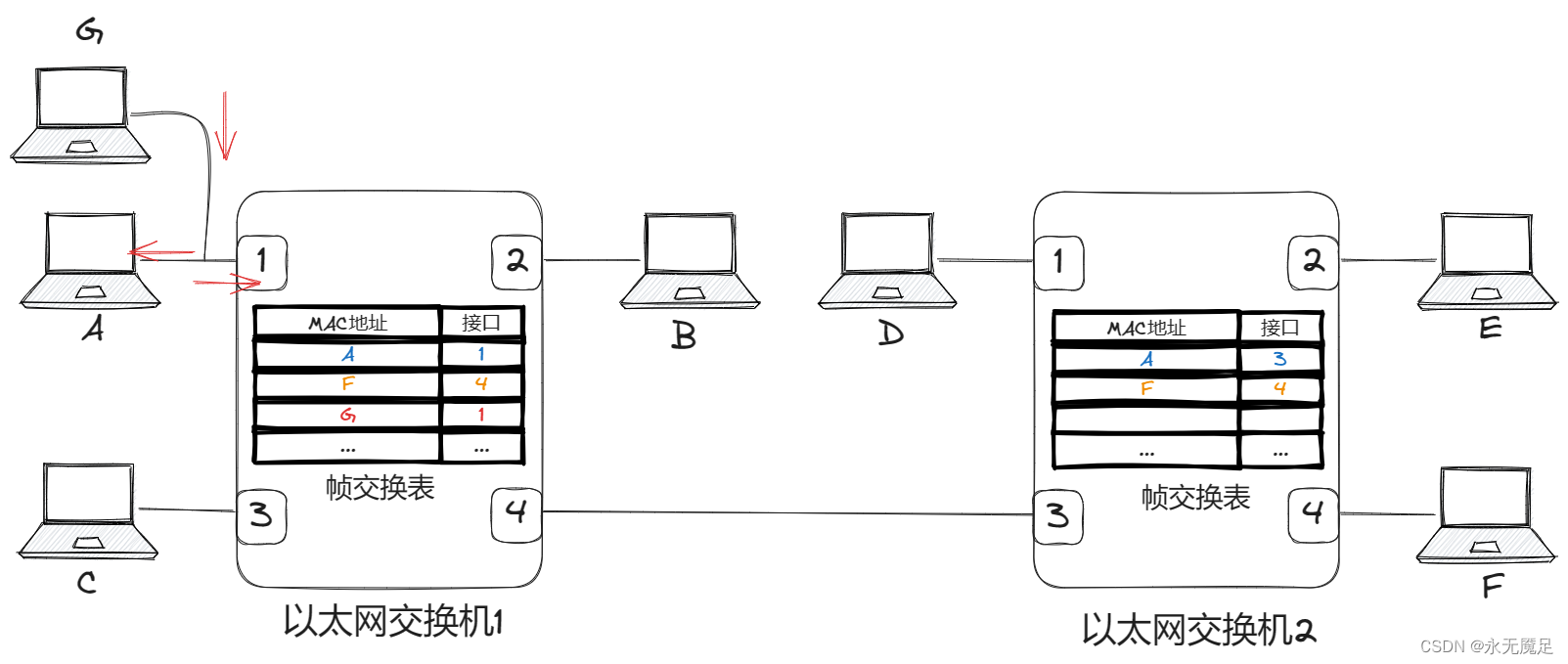
计网第三章(数据链路层)(五)
目录 一、以太网交换机自学习和转发帧的过程 1.两层交换机和三层交换机 2.以太网交换机的基本原理 3.具体实现过程 一、以太网交换机自学习和转发帧的过程 1.两层交换机和三层交换机 大家可能注意到平常做题时有叫两层交换机,或者三层交换机的。 两层交换机就…...

嵌入式系统中常见内存的划分方法
看到有小伙伴在讨论关于单片机内存的话题,今天就结合STM32给大家描述一下常见的划分区域。 在一个STM32程序代码中,从内存高地址到内存低地址,依次分布着栈区、堆区、全局区(静态区)、常量区、代码区,其中全…...

深入理解与实现:常见搜索算法的Java示例
深入理解与实现:常见搜索算法的Java示例 搜索算法在计算机科学中扮演着重要角色,用于在数据集中查找特定元素或解决问题。在本篇博客中,我们将深入探讨图算法的一个重要分支:图的搜索算法。具体而言,我们将介绍图的深…...
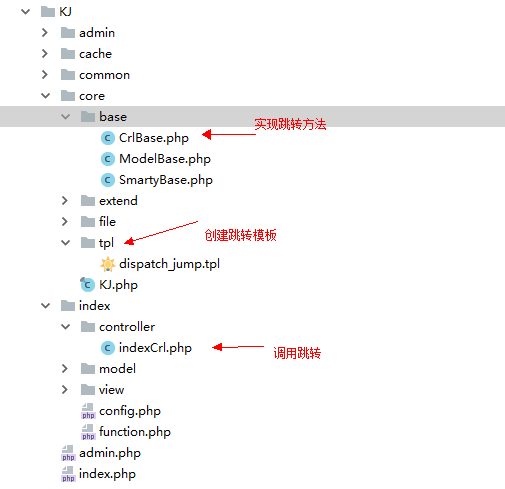
PHP自己的框架实现操作成功失败跳转(完善篇四)
1、实现效果,操作成功后失败成功自动跳转 2、创建操作成功失败跳转方法CrlBase.php /**成功后跳转*跳转地址$url* 跳转显示信息$msg* 等待时间$wait* 是否自动跳转$jump*/protected function ok($urlNULL,$msg操作成功,$wait3,$jump1){$code1;include KJ_CORE./tp…...
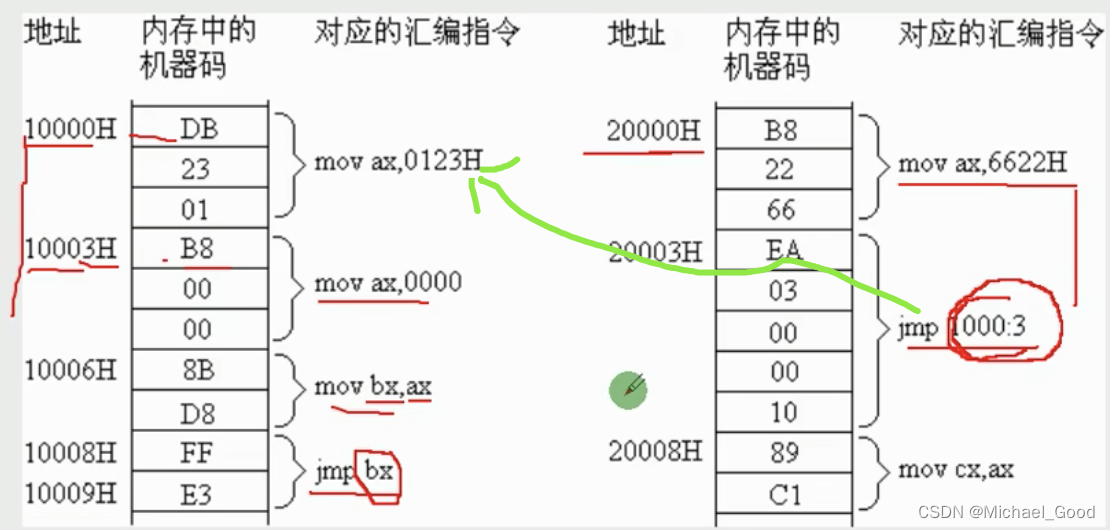
【汇编语言】CS、IP寄存器
文章目录 修改CS、IP的指令转移指令jmp问题分析 修改CS、IP的指令 理论:CPU执行何处的指令,取决于CS:IP应用:程序员可以通过改变CS、IP中的内容,进行控制CPU即将要执行的目标指令;问题:如何改变CS、IP中的…...
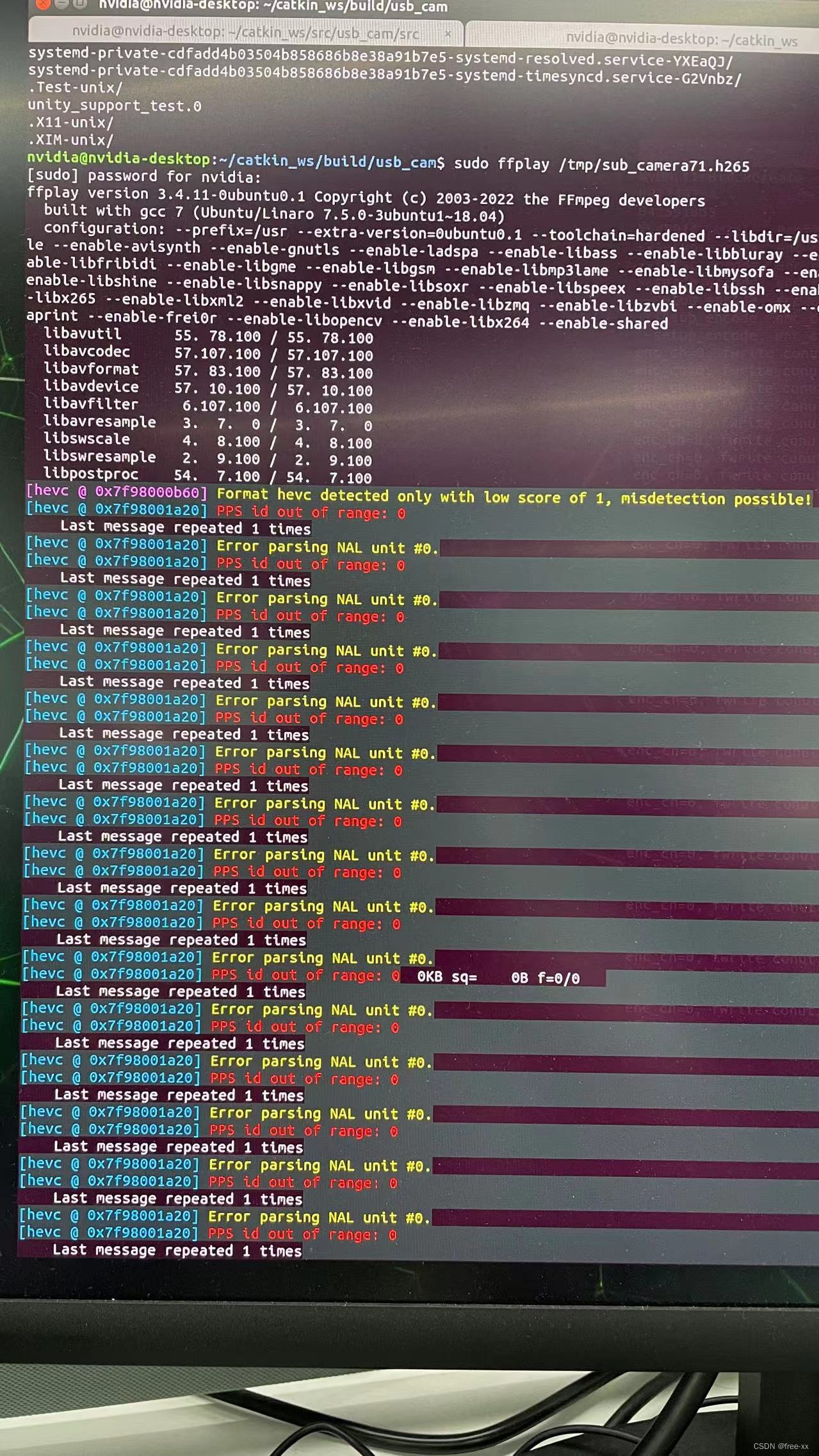
Nvidia Jetson 编解码开发(3)解决H265解码报错“PPS id out of range”
1.问题描述 基于之前的开发程序 Nvidia Jetson 编解码开发(2)Jetpack 4.x版本Multimedia API 硬件编码开发--集成encode模块_free-xx的博客-CSDN博客 通过Jetson Xavier NX 硬编码的H265发出后, 上位机断点播放发出来的H265码流, 会报“PPS id out of range” 错误 …...

Angular中如何获取URL参数?
Angular中的ActivatedRoute中保存着路由信息,可用来提取URL中的路由参数。 constructor(private route: ActivatedRoute){}ngOnInit(): void {this.getUser();}getUser(): void {const id this.route.snapshot.paramMap.get(id);} }route.snapshot是一个路由信息的…...
uniapp编写微信小程序和H5遇到的坑总结
uniapp编写微信小程序和H5遇到的坑总结 1、阻止事件冒泡2、二维码生成3、H5跨域配置4、H5时,地址栏上添加版本号5、H5时,tabBar遮挡部分内容6、uniapp使用webview通信6.1、uniapp编写的小程序嵌入h5之间的通信6.1.1、小程序向h5发送消息6.1.2、h5向小程序…...
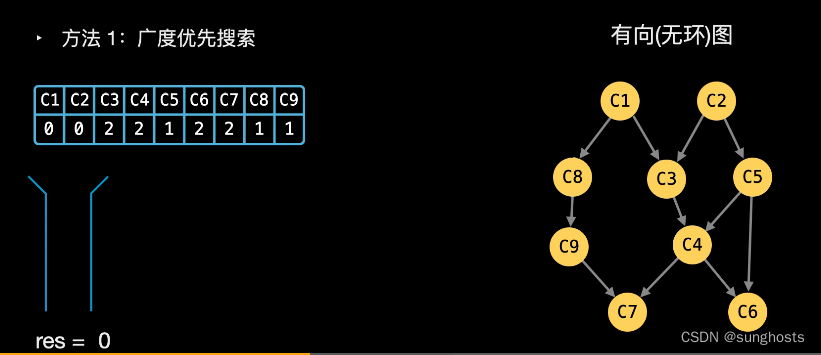
课程表-广度优先和图
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。 在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。 例如&am…...
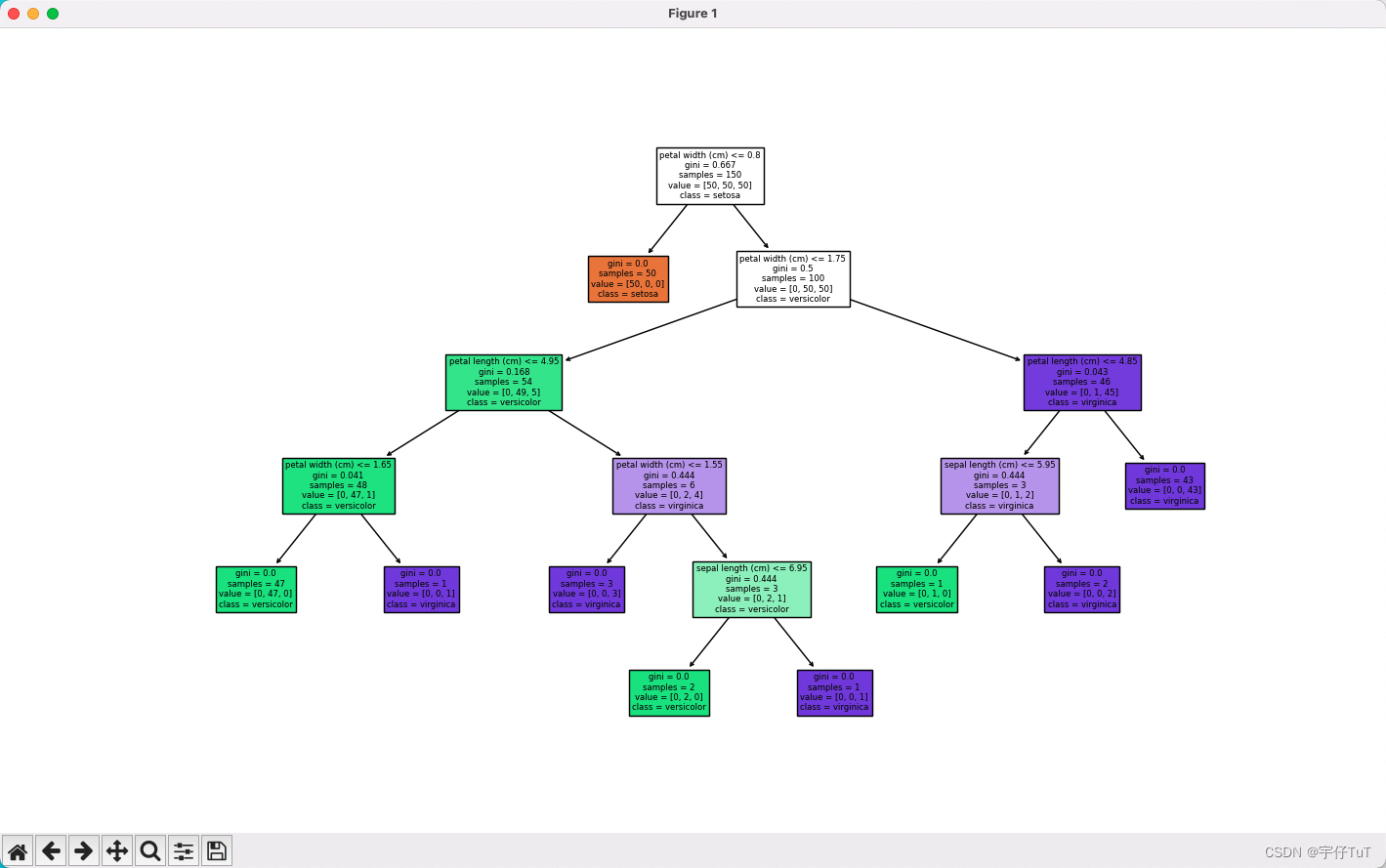
机器学习|决策树:数学原理及代码解析
机器学习|决策树:数学原理及代码解析 决策树是一种常用的监督学习算法,适用于解决分类和回归问题。在本文中,我们将深入探讨决策树的数学原理,并提供 Python 示例代码帮助读者更好地理解和实现该算法。 决策树数学原…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
