494. 目标和

原题链接：

494. 目标和

https://leetcode.cn/problems/target-sum/description/

完成情况：

解题思路：

数组回溯法

backTrack(nums, target, index+1, curSum+nums[index]);
backTrack(nums, target, index+1, curSum-nums[index]);

动态规划

	 假设P是正子集，N是负子集 例如： 假设nums = [1, 2, 3, 4, 5]，target = 3，一个可能的解决方案是+1-2+3-4+5 = 3 这里正子集P = [1, 3, 5]和负子集N = [2, 4]sum(P) - sum(N) = targetsum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)2 * sum(P) = target + sum(nums)因此，原来的问题已转化为一个求子集的和问题： 找到nums的一个子集 P，使得sum(P) = (target + sum(nums)) / 2，该式已经证明了target + sum(nums)必须是偶数，否则无解求子集的问题可以转化为01背包问题定义二维数组dp，其中dp[i][j]表示在数组下标为0...i的元素中任选元素，使得这些元素之和等于j的方案数

参考代码：

数组回溯法

package 西湖算法题解___中等题;public class __494目标和__数组回溯法 {int res = 0;public int findTargetSumWays(int[] nums, int target) {backTrack(nums,target,0,0);return res;}/**** @param nums      数组* @param target    目标值* @param index     索引位置* @param curSum    当前累计和*/private void backTrack(int[] nums, int target, int index, int curSum) {//1 <= nums.length <= 20//这种方法，属于递归，完全是因为数量级太小了//不然肯定算不出来的。if (index == nums.length){      //所有元素已经遍历完了if (curSum == target){res++;}}else{backTrack(nums, target, index+1, curSum+nums[index]);backTrack(nums, target, index+1, curSum-nums[index]);}}}

__494目标和__动态规划

package 西湖算法题解___中等题;public class __494目标和__评论区大佬 {/**题目介绍：就是说有一个数组，然后要在数组任意两两元素间插入一个【+】或者【-】最终要构成target这个值，问你有多少种拼接情况。*/public int findTargetSumWays(int[] nums, int target) {//很明显的一道dp题目，最终结果取决于过程叠加。/**假设P是正子集，N是负子集 例如： 假设nums = [1, 2, 3, 4, 5]，target = 3，一个可能的解决方案是+1-2+3-4+5 = 3 这里正子集P = [1, 3, 5]和负子集N = [2, 4]sum(P) - sum(N) = targetsum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)2 * sum(P) = target + sum(nums)因此，原来的问题已转化为一个求子集的和问题： 找到nums的一个子集 P，使得sum(P) = (target + sum(nums)) / 2，该式已经证明了target + sum(nums)必须是偶数，否则无解求子集的问题可以转化为01背包问题定义二维数组dp，其中dp[i][j]表示在数组下标为0...i的元素中任选元素，使得这些元素之和等于j的方案数*/int nLength = nums.length;//先去掉点特殊情况int sum = 0;for (int num:nums){sum += num;}// target + sum(nums)必须是偶数，否则无解     //要使target = nums[]的加减操作合，则它们必须同奇或者同偶// Math.abs(target) <= sum才有解       //目标值不能比绝对值求和还大//偶数判断还可以用   (lambda & 1) == 1   去判断if (((sum + target) & 1) == 1 || Math.abs(target) > sum){return 0;}int size = (sum + target) / 2;// 定义二维数组dp，其中dp[i][j]表示在数组下标为0...i的元素中任选元素，使得这些元素之和等于j的方案数int dp_findTargetSumWays [][] = new int[nLength][size+1];// 对dp[0][j]的初始化：除dp[0][0]和dp[0][nums[0]]外全部初始化为0// dp[0][0] = 1：nums[0]不为0时，此时dp[0][0]和dp[0][nums[0]]不重合,只有不选nums[0]，其总和为0// dp[0][0] = 2：nums[0]为0时，此时dp[0][0]和dp[0][nums[0]]重合，选或者不选nums[0]，其总和都为0if (nums[0] <= size){dp_findTargetSumWays[0][nums[0]] = 1;}if (nums[0] == 0){dp_findTargetSumWays[0][0] = 2;}else {dp_findTargetSumWays[0][0] = 1;}// 对dp[i][0]的初始化，可以放在下面整个dp的递推代码中for (int i = 1;i<nLength;i++){if (nums[i] == 0){//当nums[1]为0时，选择或者不选择nums[1]都可以使总和为0，//即dp[i][0] = dp[i - 1][0] + dp[i - 1][0 - nums[i]] = 2 * dp[i -1][0]dp_findTargetSumWays[i][0] = 2*dp_findTargetSumWays[i-1][0];}else{// 当nums[i]不为0时，只有不选nums[i]才可以使总和为0dp_findTargetSumWays[i][0] = dp_findTargetSumWays[i-1][0];}}// dp[i][j]递推：由于初始化时都将i = 0和j = 0的情况已经赋值，所以直接从i = 1和j = 1开始// 完全可以将上面对dp[i][0]的初始化放在此处，只需要将j从0开始for (int i=1;i<nLength;i++){for (int j=1;j<=size;j++){if (j>=nums[i]){dp_findTargetSumWays[i][j] = dp_findTargetSumWays[i-1][j] + dp_findTargetSumWays[i-1][j-nums[i]];}else{dp_findTargetSumWays[i][j] = dp_findTargetSumWays[i-1][j];}}}return dp_findTargetSumWays[nLength-1][size];}
}

经验吸取

1. 首先，如果最终结果可以由其中的每一步过程，造成影响得来，那么就可以考虑用dp

2. dp的难点就在于状态转移方程！！！如何将一个问题转化很重要！！！

3. 转化形式应该为：
   
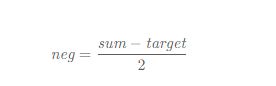
   未知状态 = 已知确定目标值
   

   dp数组过程推演情况。