CSS行内,内部,外部以及优先级
1.内联样式表:
将样式编写到style标签里
<style>.context {color: red;}
</style>2. 行内样式:
在 HTML 标签中使用 style 属性设置 CSS 样式
<div style="font-size: 18px;">行内样式</div>3.外联样式:
使用 link标签引入外部css文件
<link rel="stylesheet" href="table.css">优先级:
内联样式> 内部样式 > 外部样式
相关文章:

CSS行内,内部,外部以及优先级
1.内联样式表: 将样式编写到style标签里 <style>.context {color: red;} </style> 2. 行内样式: 在 HTML 标签中使用 style 属性设置 CSS 样式 <div style"font-size: 18px;">行内样式</div> 3.外联样式࿱…...

LCA——最近公共祖先
LCA问题是指在一棵树中找到两个节点的最近公共祖先。最近公共祖先是指两个节点在树中的最近的共同祖先节点。例如,在下面这棵树中,节点 6 6 6和节点7的最近公共祖先是节点 3 3 3。 1/ \2 3/ \ / \4 5 6 7解决LCA问题的方法有很多种ÿ…...

游戏开发与硬件结合,开启全新游戏体验!
游戏与硬件的结合可以通过多种方式实现,从改善游戏体验到创造全新的游戏玩法。以下是一些常见的游戏与硬件结合的方式: 虚拟现实(VR)和增强现实(AR)技术:VR和AR技术使玩家能够沉浸式地体验游戏…...
测试框架pytest教程(4)运行测试
运行测试文件 $ pytest -q test_example.py 会运行该文件内test_开头的测试方法 该-q/--quiet标志使输出保持简短 测试类 pytest的测试用例可以不写在类中,但如果写在类中,类名需要是Test开头,非Test开头的类下的test_方法不会被搜集为用…...
Linux 上 离线部署GeoScene Server Py3 运行时环境
默认安装ArcGIS Pro的时候,会自动部署上Python3环境,所以在windows上不需要考虑这个问题,但是linux默认并不部署Py3,因此需要单独部署,具体部署可以参考Linux 上 ArcGIS Server 的 Python 3 运行时—ArcGIS Server | A…...

Python+request+unittest实现接口测试框架集成实例
这篇文章主要介绍了Pythonrequestunittest实现接口测试框架集成实例,小编觉得挺不错的,现在分享给大家,也给大家做个参考。一起跟随小编过来看看吧 1、为什么要写代码实现接口自动化 大家知道很多接口测试工具可以实现对接口的测试…...
django/flask+python+vue汽车租赁管理系统_1ma2x
开发语言:Python 框架:django/flask Python版本:python3.7.7 数据库:mysql 数据库工具:Navicat 开发软件:PyCharm . 课题主要分为三大模块:即管理员模块、用户模块和普通管理员模块࿰…...

胜者打仗,就像高山上决开积水,势不可挡
胜者打仗,就像高山上决开积水,势不可挡 【安志强趣讲《孙子兵法》16讲】 【原文】 是故胜兵先胜而后求战,败兵先战而后求胜。善用兵者,修道而保法,故能为胜败之政。 【注释】 修道:指从各方面修治“先立于不…...

stm32的命令规则
stm32型号的说明:以STM32F103RBT6这个型号的芯片为例,该型号的组成为7个部分,其命名规则如下:...
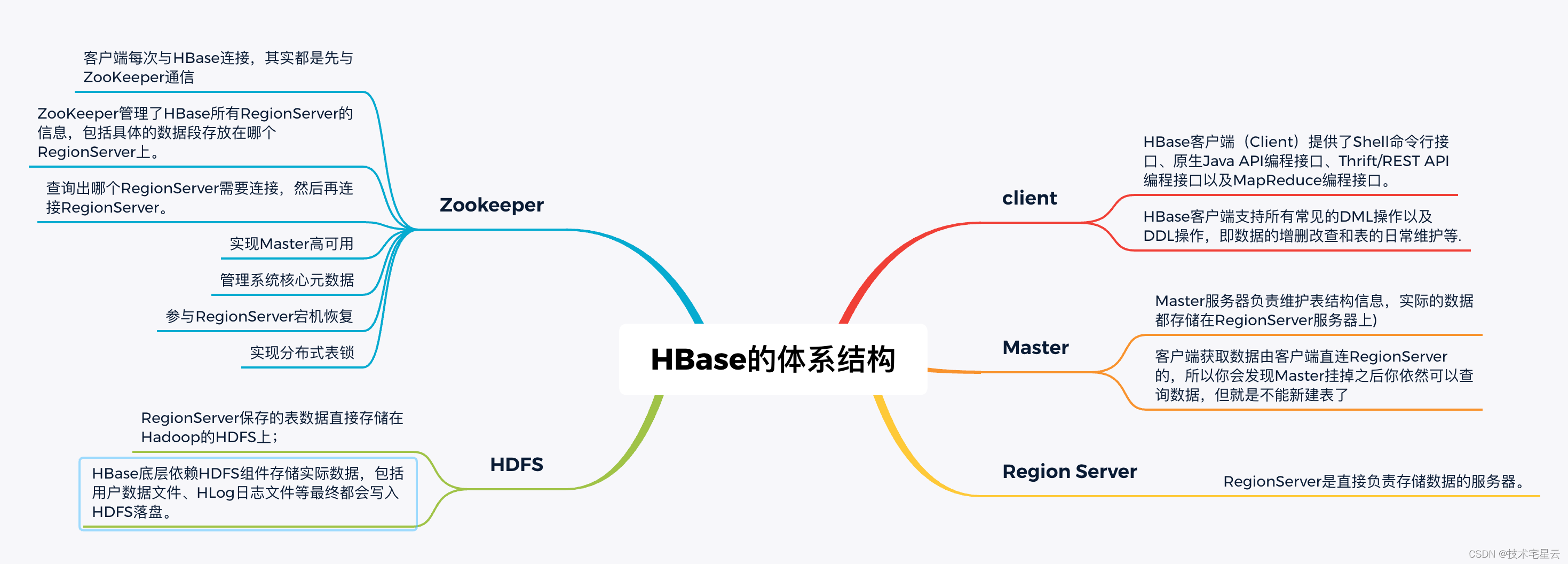
1. HBase中文学习手册之揭开Hbase的神秘面纱
揭开Hbase的神秘面纱 1.1 欢迎使用 Apache Hbase1.1.1 什么是 Hbase?1.1.2 Hbase的前世今生1.1.3 HBase的技术选型?1.1.3.1 不适合使用 HBase的场景1.1.3.2 适合使用 HBase的场景 1.1.4 HBase的特点1.1.4.1 HBase的优点1.1.4.2 HBase的缺点 1.1.5 HBase设计架构 1.…...
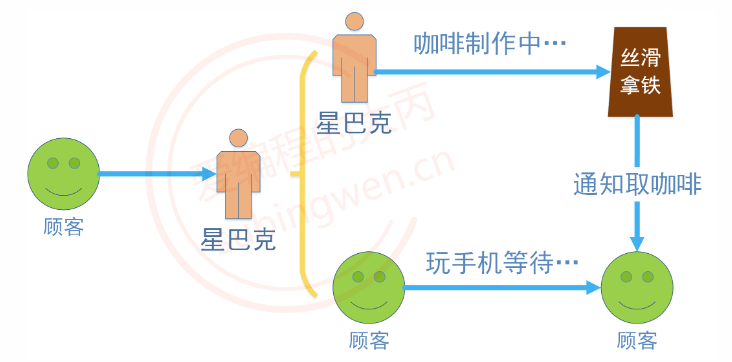
[线程/C++]线程同(异)步和原子变量
文章目录 1.线程的使用1.1 函数构造1.2 公共成员函数1.2.1 get_id()1.2.2 join()2.2.3 detach()2.2.5 joinable()2.2.6 operator 1.3 静态函数1.4 call_once 2. this_thread 命名空间2.1 get_id()2.2 sleep_for()2.3 sleep_until()2.4 yield() 3. 线程同步之互斥锁3.1 std:mute…...

全球网络加速器GA和内容分发网络CDN,哪个更适合您的组织使用?
对互联网用户来说,提供最佳的用户体验至关重要:网页加载时间过长、视频播放断断续续以及服务忽然中断等问题都足以在瞬间失去客户。因此可以帮助提高您的网站或APP提高加载性能的解决方案就至关重要:全球网络加速器和CDN就是其中的两种解决方…...
蓝凌OA custom.jsp 任意文件读取
曾子曰:“慎终追远,民德归厚矣。” 漏洞复现 访问漏洞url: 出现漏洞的文件为 custom.jsp,构造payload: /sys/ui/extend/varkind/custom.jsp var{"body":{"file":"file:///etc/passwd&q…...
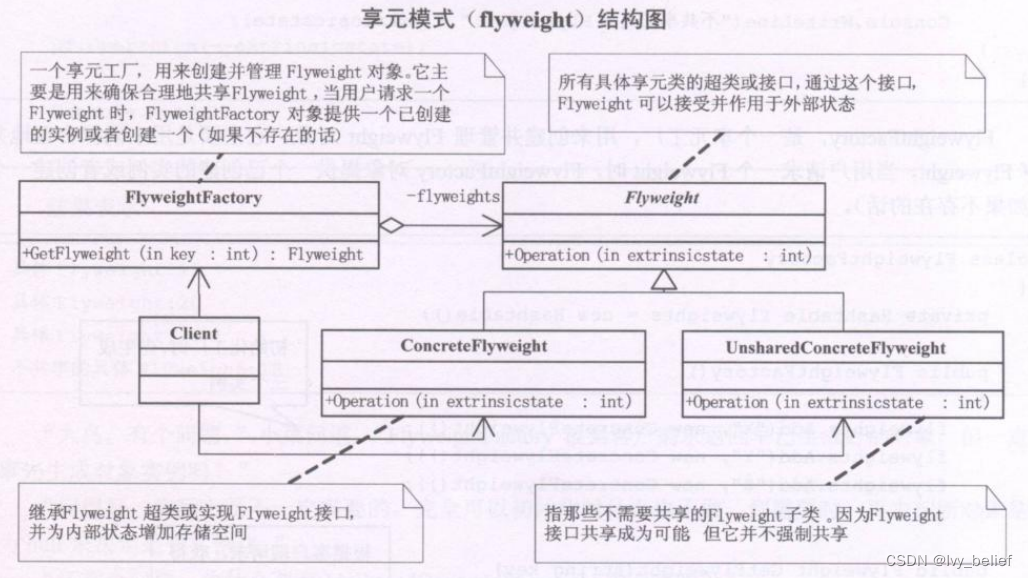
(二)结构型模式:7、享元模式(Flyweight Pattern)(C++实例)
目录 1、享元模式(Flyweight Pattern)含义 2、享元模式的UML图学习 3、享元模式的应用场景 4、享元模式的优缺点 5、C实现享元模式的简单实例 1、享元模式(Flyweight Pattern)含义 享元模式(Flyweight)…...

laravel 多次查询请求,下次请求清除上次请求的where 条件
在Laravel中,可以使用where方法来添加查询条件,但是每次添加where条件时,都会在查询构造器中持久化这些条件,直到你手动重置它们。所以,如果你想在下一次查询中清除上次查询的where条件,有以下几种选择&…...

C++根据如下使用类MyDate的程序,写出类MyDate的定义,MyDate中有三个数据成员:年year,月month,日day完成以下要求
题目: 根据如下使用类MyDate的程序,写出类MyDate的定义,MyDate中有三个数据成员: 年year,月month,日day int year,month,day; void main() { MyDate d1, d2; d1.set(2015, 12, 31); d2.set(d1); d1.…...
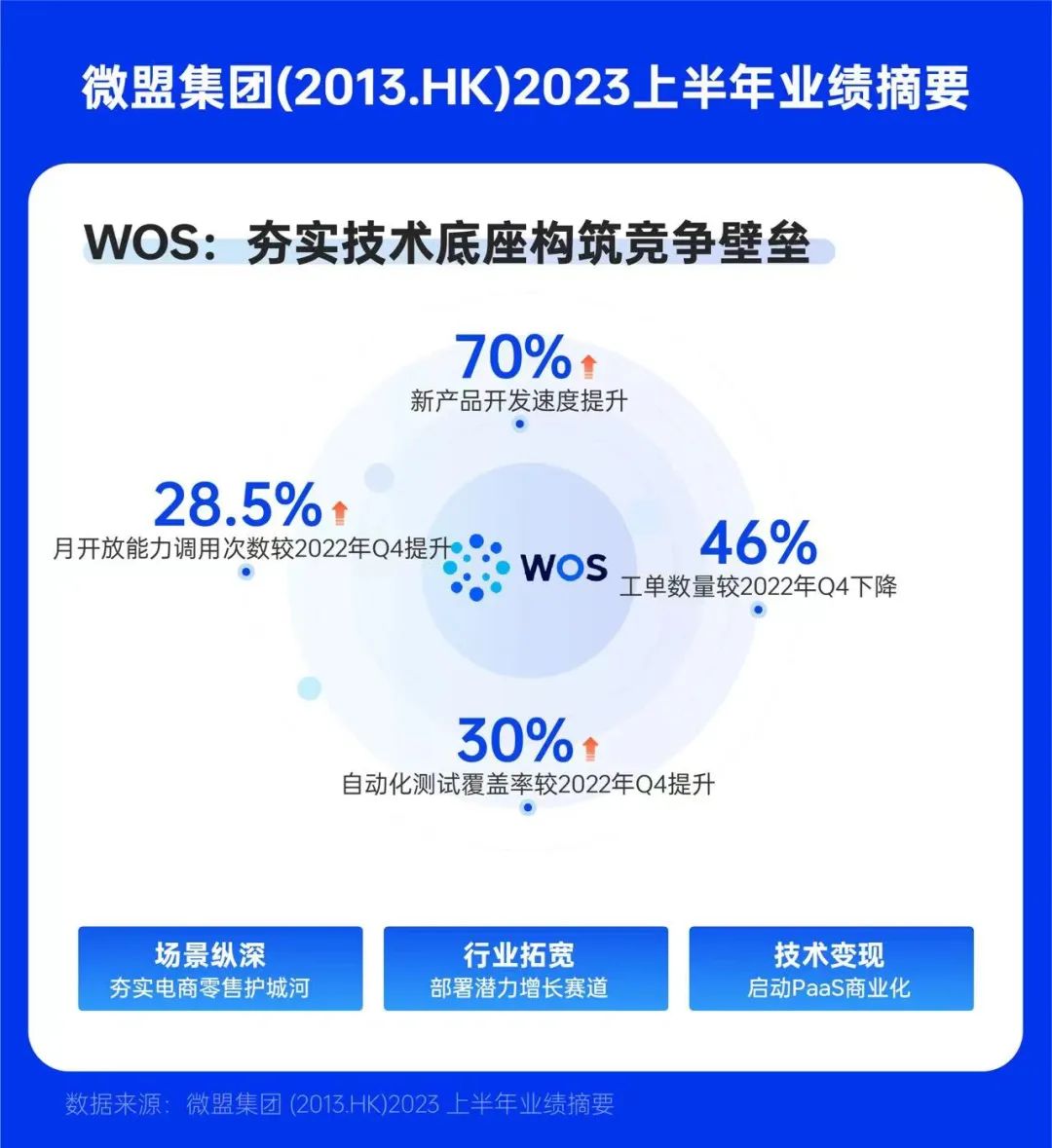
微盟集团中报增长稳健 重点发力智慧零售AI赛道
零售数字化进程已从渠道构建走向了用户的深度运营。粗放式用户运营体系无法适应“基于用户增长所需配套的精细化运营能力”,所以需要有个体、群体、个性化、自动化运营——即在对的时候、以对的方式、把对的内容推给用户。 出品|产业家 2023年已经过半,经济复苏成为…...
模板方法模式)
设计模式(7)模板方法模式
一、定义: 定义一个操作中的算法骨架,而将算法的一些步骤延迟到子类中,使得子类可以不改变该算法结构的情况下重定义该算法的某些特定步骤。它是一种类行为型模式。 //模板方法抽象类 public abstract class AbstractClass {//模板方法publ…...

2308C++协程流程9
参考 #include <协程> #include "简异中.cpp" //用来中文定义的.元<类 T>构 P;元<类 T>构 任务{用 承诺型P<T>;任务()默认;动 符号 协待()常 无异{构 等待器{极 直接协()常 无异{中 p.是准备好();}协柄 挂起协(协柄<>o)常 无异{p.连续…...

基于学习交流社区的自动化测试实现
一 项目介绍 项目名称 项目名称: 学习交流社区 项目介绍 项目介绍: 学习交流社区是一个基于Spring的前后端分离的在线论坛系统。使用了MySQL数据库来存储相关信息,项目完成后使用Xshell将其部署到云服务器上。 前端页面: 前端共由…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
