线段树详解——影子宽度
OK,今天来讲一讲线段树~~
- 线段树是什么
- 线段树的实现
- 线段树的时间复杂度
- 线段树的应用
- 线段树的节点结构
- 其他操作和优化
- 例题——影子宽度
- 输入输出格式
- 输入格式
- 输出格式
- 输入输出样例
- 输入样例
- 输出样例
- 例题讲解
线段树是什么
线段树( S e g m e n t Segment Segment T r e e ~~Tree Tree)是一种二叉树,用于区间查询。线段树的每个节点表示一个区间,根节点表示整个区间,子节点表示区间的一半。线段树的典型应用是解决区间查询问题,例如区间最大值、区间最小值等。
线段树的实现
线段树的构建过程可以通过递归实现。给定一个数组 a r r arr arr,线段树的根节点表示 a r r [ 0 ] arr[0] arr[0]到 a r r [ n − 1 ] arr[n-1] arr[n−1]之间的区间和(或其他区间操作)。根节点的左子节点表示 a r r [ 0 ] arr[0] arr[0]到 a r r [ ( n − 1 ) / 2 ] arr[(n-1)/2] arr[(n−1)/2]之间的区间和,右子节点表示 a r r [ ( n − 1 ) / 2 + 1 ] arr[(n-1)/2+1] arr[(n−1)/2+1]到 a r r [ n − 1 ] arr[n-1] arr[n−1]之间的区间和。依次类推,直到区间被划分为长度为1的节点。
线段树的每个节点都会记录该节点表示的区间的一些统计信息,例如区间和、区间最大值、区间最小值等。该统计信息可以通过节点的左子节点和右子节点的统计信息来计算得到。
当要查询的区间与当前节点表示的区间有重叠时,查询操作会继续向下递归。当要查询的区间与当前节点表示的区间完全相等时,查询操作可以直接返回当前节点的统计信息。当要查询的区间在当前节点表示的区间的左半部分时,查询操作会向左子节点递归。当要查询的区间在当前节点表示的区间的右半部分时,查询操作会向右子节点递归。
当要更新的位置在当前节点表示的区间内时,更新操作会继续向下递归。当更新到叶子节点时,将该位置的值更新为给定的新值。然后,更新操作会向上递归,将更新后的值传递给父节点并重新计算父节点的统计信息。
线段树的时间复杂度
线段树的时间复杂度为 O ( l o g ( n ) ) O(log(n)) O(log(n)),其中n为数组的长度。这是因为构建线段树需要对每个节点进行一次操作,总共需要 O ( n ) O(n) O(n)的时间。查询操作的时间复杂度为 O ( l o g ( n ) ) O(log(n)) O(log(n)),因为查询的过程类似于二分查找,每次将查询范围缩小一半,最多需要递归 l o g ( n ) log(n) log(n)次。更新操作的时间复杂度也为 O ( l o g ( n ) ) O(log(n)) O(log(n))。
线段树是一种非常强大的数据结构,可以用于解决各种区间查询问题。然而,线段树的应用并不局限于时间复杂度为 O ( l o g ( n ) ) O(log(n)) O(log(n))的问题,它还可以结合其他数据结构和算法来实现更高效的解决方案。例如,线段树可以与离散化、树状数组等结合使用,用于解决动态区间查询问题。同时,线段树还可以用于解决一些特殊情况下的区间查询问题,例如动态维护滑动窗口中的最大值、最小值等。
线段树的应用
线段树的应用非常广泛,以下是一些常见的应用场景:
-
区间最小值/最大值查询:通过线段树可以在 O ( l o g ( n ) ) O(log(n)) O(log(n))的时间内找到任意区间的最小值或最大值。这在处理动态数据的情况下非常有用,例如动态维护滑动窗口的最小值、最大值。
-
区间和查询:线段树可以用来快速计算区间内所有元素的和。这在求解数组范围内的连续子数组和、处理区间加法或区间更新操作等问题非常有用。
-
区间更新:线段树可以将区间内的某个值更新为新值。这在处理动态修改数据的情况下非常有用,例如修改数组某个位置的值,或者将区间内的所有元素增加某个固定值。
-
区间统计:除了求和、最小值、最大值等基本操作外,线段树还可以做更复杂的区间统计操作。例如,可以通过线段树求解区间内的第 k k k小元素,或者统计区间内有多少个不同的元素等。
-
离散化:离散化是一种将连续的数据映射到离散的区间中的方法。通过使用线段树可以很方便地实现离散化操作,将大量的连续数据映射到有限的离散区间内,从而减小数据规模,提高查询效率。
-
区间交集查询:线段树可以用于判断两个区间是否有交集,以及计算出两个区间的交集。这在处理区间重叠问题、查找共同区间等场景下非常有用。
-
区间覆盖查询:线段树可以用于快速查找某个区间是否完全被覆盖,以及计算出所有覆盖某个区间的区间。这在处理区间合并、区间分割等问题非常有用。
线段树是一种非常强大而灵活的数据结构,可以根据需求进行扩展和优化。通过合理地设计数据结构和算法,线段树可以高效地解决各种区间查询问题,提高程序的性能和可扩展性。
线段树的节点结构
线段树的节点结构一般包含以下几个属性:
start 和 end:表示当前节点所代表的区间的起始和结束位置。
一个外挂:依题目而定
其他操作和优化
线段树还可以进行一些其他的操作和优化,例如:
- 惰性更新:使用标记来延迟更新,减少更新操作的次数,提高效率。
- 区间增量:维护区间值的增量,而不是直接修改区间的值,可以减少更新操作的次数。
- 动态修改:支持在原始数据的基础上进行修改,而不需要重新构建整个线段树。
例题——影子宽度
精灵王的桌子上零散地放着若干个盒子,桌子的后方是一堵墙。如下图所示。现在从桌子的前方射来一束平行光,把盒子的影子投射到了墙上。问影子的总宽度是多少?
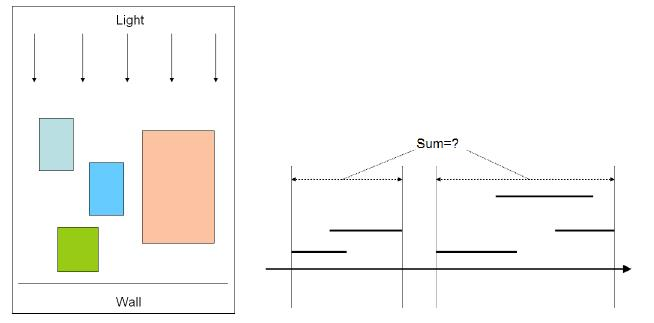
输入输出格式
输入格式
- 第1行:盒子的个数N(1≤=N≤10000)。
- 第2…N+1行:每个盒子的起始位置S和结束位置T(1≤S, T≤100000)。
输出格式
- 第1行:包含一个整数,表示影子的总宽度。
输入输出样例
输入样例
4
1 2
3 5
4 6
5 6
输出样例
4
例题讲解
这题纯纯版题呀!!
#include <bits/stdc++.h>
using namespace std;
const int N=120000;
int n,m,maxx,minn,a[N],b[N],cover[4*N];
void insert(int idx,int ll,int rr,int x,int y) {if (x<=ll && y>=rr) //如果区间范围包含当前线段cover[idx]=1;if(cover[idx]==1) //如果当前线段已经被标记了return;int mid=(ll+rr)/2;if (y<=mid)insert(idx*2,ll,mid,x,y); //左子树递归else if (x>=mid)insert(idx*2+1,mid,rr,x,y); //右子树递归else { //拆分成两边,分别递归insert(idx*2,ll,mid,x,y);insert(idx*2+1,mid,rr,x,y);}
}
int count(int idx,int ll,int rr,int x,int y) {if (cover[idx]==1) //如果当前线段被标记return rr-ll; //返回长度if (rr-ll>1) { //如果当前线段还是一个线段int mid=(ll+rr)/2;int tx=count(idx*2,ll,mid,x,y);int ty=count(idx*2+1,mid,rr,x,y);return tx+ty;}return 0;
}
int main() {scanf ("%d",&n);for (int i=1;i<=n;i++) {scanf("%d%d",&a[i],&b[i]);if (a[i]>maxx)maxx=a[i];if (a[i]<minn)minn=a[i];if (b[i]>maxx)maxx=b[i];if (b[i]<minn)minn=b[i];//一堆判断,求最大边界和最小边界//有时候 是输入的数}for (int i=1;i<=n;i++)insert(1,minn,maxx,a[i],b[i]); //标记线段printf("%d",count(1,minn,maxx,minn,maxx)); //输出结果return 0;
}
相关文章:

线段树详解——影子宽度
OK,今天来讲一讲线段树~~ 线段树是什么线段树的实现线段树的时间复杂度线段树的应用线段树的节点结构其他操作和优化例题——影子宽度输入输出格式输入格式输出格式 输入输出样例输入样例输出样例 例题讲解 线段树是什么 线段树( S e g m e n t Segmen…...
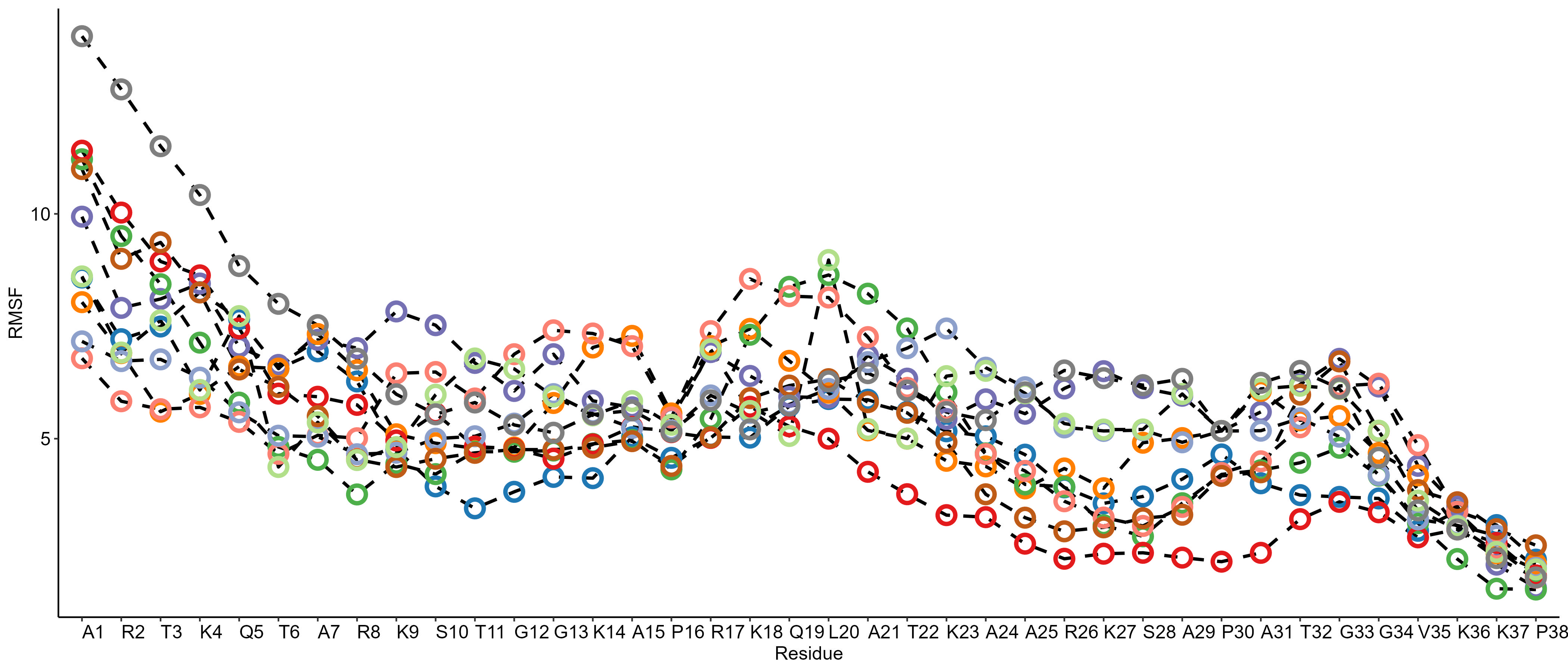
使用R语言绘制折线图
写在前面 昨天我们分享了使用Python绘制折线图的教程,跟着NC学作图 | 使用python绘制折线图,考虑到很多同学基本不使用Python绘图。那么,我们也使用R语言复现此图形。 此外,在前期的教程中,我们基本没有分享过折线图的教程。因此,我们在这里也制作一期关于折线图的教程。…...

无涯教程-Perl - wantarray函数
描述 如果当前正在执行的函数的context正在寻找列表值,则此函数返回true。在标量context中返回false。 语法 以下是此函数的简单语法- wantarray返回值 如果没有context,则此函数返回undef;如果lvalue需要标量,则该函数返回0。 例 以下是显示其基本用法的示例…...
【gitkraken】gitkraken自动更新问题
GitKraken 会自动升级!一旦自动升级,你的 GitKraken 自然就不再是最后一个免费版 6.5.1 了。 在安装 GitKraken 之后,在你的安装目录(C:\Users\<用户名>\AppData\Local\gitkraken)下会有一个名为 Update.exe 的…...

《Java Web程序设计》试卷03
《Java Web程序设计》试卷03 课程编码: 301209 适用专业: 计算机应用(包括JAVA方向) 注 意 事 项 1、首先按要求在试卷标封处填写你所在的系(部)、专业、班级及学号和姓名; 2、仔细阅读各类题目的回答要求,…...
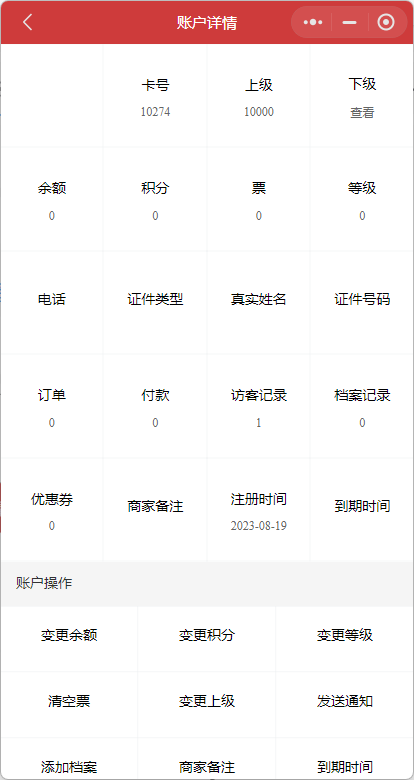
怎么查看小程序中的会员信息
商家通过查看会员信息,可以更好地了解用户,并为他们提供更个性化的服务和推荐。接下来,就将介绍如何查看会员信息。 商家在管理员后台->会员管理处,可以查看到会员列表。支持搜索会员的卡号、手机号和等级。还支持批量删除会员…...

网络安全—黑客—自学笔记
想自学网络安全(黑客技术)首先你得了解什么是网络安全!什么是黑客! 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全…...
深度解读波卡 2.0:多核、更有韧性、以应用为中心
本文基于 Polkadot 生态研究院整理,有所删节 随着波卡 1.0 的正式实现,波卡于 6 月 28 日至 29 日在哥本哈根举办了年度最重要的会议 Polkadot Decoded 2023,吸引了来自全球的行业专家、开发者和爱好者,共同探讨和分享波卡生态的…...

微服务中间件--Eureka注册中心
Eureka注册中心 a.eureka原理分析b.搭建eureka服务c.服务注册d.服务发现 a.eureka原理分析 1.每个服务启动时,将自动在eureka中注册服务信息 (每个服务每隔30秒发送一次的心跳续约,当某个服务没有发送时,eurekaServer将自动剔除该服务&#x…...
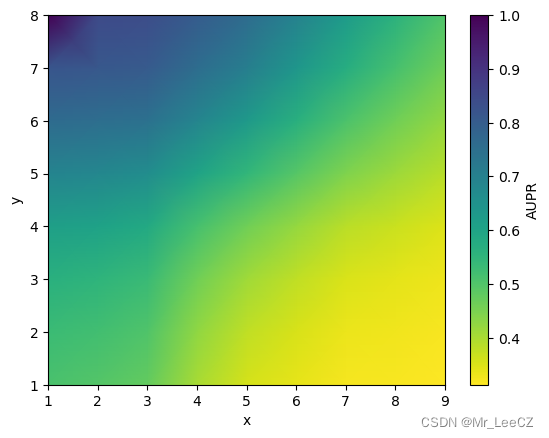
积跬步至千里 || 矩阵可视化
矩阵可视化 矩阵可以很方面地展示事物两两之间的关系,这种关系可以通过矩阵可视化的方式进行简单监控。 定义一个通用类 from matplotlib import pyplot as plt import seaborn as sns import numpy as np import pandas as pdclass matrix_monitor():def __init…...

zookeeper详细介绍
ZooKeeper是一个开源的分布式协调服务,具有以下一些关键特点: 数据模型 ZooKeeper的数据模型采用层次化的多叉树形结构,每个节点称为znode,类似于文件系统中的文件和目录。每个znode可以存储数据和控制信息。一致性保证 ZooKeeper通过ZAB协议,实现分布式环境下数据的强一致性,…...

面板市场趋势分析:价格上涨势头或将减缓 | 百能云芯
8月末,面板价格报价公布,市场研究机构TrendForce指出,电视面板今年以来已经上涨超过30%,虽然下游品牌商对于价格上涨提出了不同声音,但由于面板厂商采取了按需生产的策略,8月仍然出现了3~5%的价格上涨。Tre…...
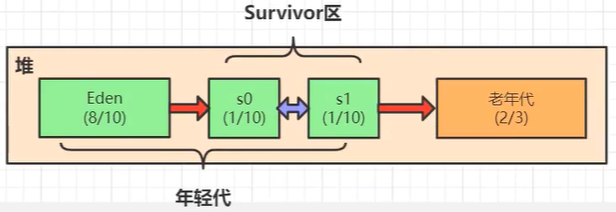
JVM性能调优
java 如何跨平台,如何一次编译到处执行 是由于java在不同的jvm上编译,jvm在软件层面屏蔽不同操作系统在底层硬件与指令上的区别。 jvm 包括 new 的对象都是放在堆中 栈,给线程单独使用(线程私有),存储一个…...

【全链路追踪】XXL-JOB添加TraceID
文章目录 一、背景调用路径部署环境问题 二、方案三、Demo示例1、MDC2、RequestInterceptor3、HandlerInterceptor4、logback.xml 四、后续改进思路 一、背景 首先这个项目属于小型项目,由于人手以及时间限制,并未引入Skywalking等中间件来做调用链路追…...

[Unity]Lua本地时间、倒计时和正计时。
惯例,直接上代码: --正计时开始时的时间戳 self.begin_time os.time() --倒计时时长,01:30:00 self.countdown_time 5400 --是否开始计时 self.is_update_local_time true--Unity Update function time_transition:update_local_timer()i…...

探究HTTP API接口测试:工具、方法与自动化
本文将深入探讨HTTP API接口测试的重要性,并介绍了相关工具、方法以及自动化测试的实施,同时比较了HTTP和API接口测试的区别。从不同角度解析这一关键测试领域,帮助读者更好地理解和应用于实际项目中。 在如今数字化的世界中,软件…...

CSS中如何实现文字溢出省略号(text-overflow: ellipsis)效果?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ CSS中如何实现文字溢出省略号(text-overflow: ellipsis)效果?⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 …...
)
CSDN编程题-每日一练(2023-08-21)
CSDN编程题-每日一练(2023-08-21) 一、题目名称:贝博士的论文审阅统计二、题目名称:生命进化书三、题目名称:寻找宝藏山一、题目名称:贝博士的论文审阅统计 时间限制:1000ms内存限制:256M 题目描述: 贝博士经常收到申请他审阅论文的信函,每封信函的信封上面只有两个申…...
:React中的事件绑定如何实现?有几种方式?)
面试题-React(四):React中的事件绑定如何实现?有几种方式?
一、React事件绑定机制 在React中,事件绑定是通过JSX语法来实现的。你可以将事件处理函数直接绑定到元素的属性上,比如onClick、onMouseOver等。当触发相应事件时,绑定的事件处理函数将被调用。 React采用了一种合成事件(Synthe…...
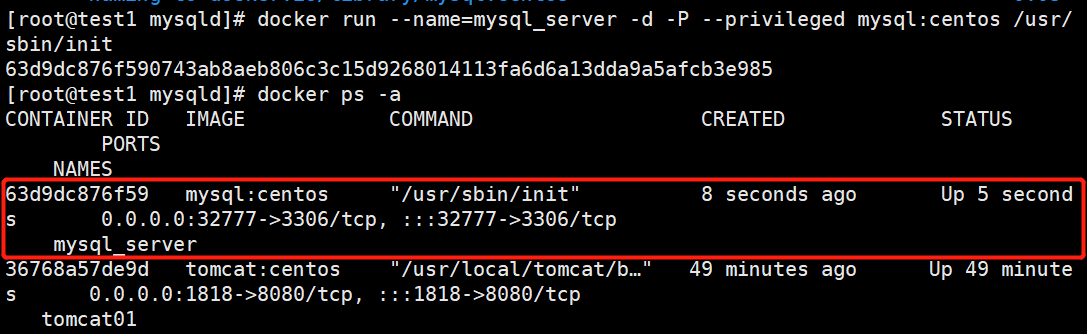
Docker容器:docker镜像的创建及dockerfile案例
文章目录 一.docker镜像的三种创建方法1.基于现有镜像创建1.1 启动镜像1.2 生成新镜像 2.基于本地模板创建2.1 OPENVZ 下载模板2.2 导入容器生成镜像 3.基于dockerfile创建3.1 dockerfile结构及分层3.2 联合文件系统3.3 docker镜像加载原理及过程 4.dockerfile操作常用的指令4.…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
