算法|Day46 动态规划14
LeetCode 1143- 最长公共子序列
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目描述:给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
解题思路
- 确定dp数组(dp table)以及下标的含义
dp[i][j],代表字符串1 从0到i-1 字符串2 从0到j-1为止,两个字符的最长公共子序列。
为什么要这样定义呢,方便dp数组的初始化,若dp[i][j]代表从0-i最长公共子序列,那我们dp[0][i]就都得判断,看是否两个对应位置字符相等,来进行初始化。
- 确定递推公式
和上一题一样,如果两个对应位字符相等,则使得
- dp数组如何初始化
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
- 如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
- 如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
- 确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历。
- 举例推导dp数组
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1.size()][text2.size()];}
};总结:
- 如果当前俩字符不想等时,取前面字符的最大值,这是和上一题不同的地方。
LeetCode 1035- 不相交的线
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目描述:在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
- nums1[i] == nums2[j]
- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
解题思路
本题和上一题一模一样,因为我们这题要找不相交的,所以我们找到两个数组的最长公共子序列就一定可以。
1.确定dp数组(dp table)以及下标的含义
dp[i][j],代表字符串1 从0到i-1 字符串2 从0到j-1为止,两个字符的最长公共子序列。
为什么要这样定义呢,方便dp数组的初始化,若dp[i][j]代表从0-i最长公共子序列,那我们dp[0][i]就都得判断,看是否两个对应位置字符相等,来进行初始化。
2.确定递推公式
和上一题一样,如果两个对应位字符相等,则使得
3.dp数组如何初始化
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
- 如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
- 如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
4.确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历。
5.举例推导dp数组
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int s1 = nums1.size();int s2 = nums2.size();vector<vector<int>> dp(s1+1,vector<int>(s2+1,0));for(int i=1;i<=s1;i++){for(int j=1;j<=s2;j++){if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1] + 1;}else{dp[i][j] = max(dp[i-1][j],dp[i][j-1]);}}}return dp[s1][s2];}
};总结:
- 和上一题一样的
LeetCode 53- 最大子数组和
题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题目描述:给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
解题思路
- 确定dp数组(dp table)以及下标的含义
dp[i]:以i为结尾的连续子数组的最大的和。
- 确定递推公式
dp[i] = max(dp[i-1]+nums[i],nums[i]);
- dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
- nums[i],即:从头开始计算当前连续子序列和
- dp数组如何初始化
全部初始化为0
- 确定遍历顺序
顺序遍历
- 举例推导dp数组
class Solution {
public://没AC是因为开始把res设置为了int的最小值,应该设置为nums[0]的int maxSubArray(vector<int>& nums) {vector<int> dp(nums.size(),0);int res = nums[0];if(nums.size() == 1) return nums[0];dp[0] = nums[0];for(int i=1;i<nums.size();i++){dp[i] = max(dp[i-1]+nums[i],nums[i]); res = max(res,dp[i]);}return res;}
};总结:
- 本题开始一直错,是初始化res错了,一直初始化成int最小值,那么如果就两个数的时候,它就会取第二个数。因为我们i是从1开始的,所以一直错。
相关文章:

算法|Day46 动态规划14
LeetCode 1143- 最长公共子序列 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目描述:给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ÿ…...
宠物小程序开发攻略:五分钟教你打造宠物店小程序
随着互联网技术的发展和智能手机的普及,小程序成为了各行各业的新宠。宠物服务行业也不例外,宠物店通过搭建小程序,可以实现线上线下的结合,提供更便捷的服务和更优质的用户体验。那么,宠物服务小程序的制作流程是怎样…...

open suse 15.5(任意版本) 使用阿里云的repo
一、shell suse 的包管理工具叫 zypper. zypper addrepo -f http://mirrors.aliyun.com/opensuse/distribution/leap/15.5/repo/oss/ openSUSE-15.5-Oss zypper addrepo -f http://mirrors.aliyun.com/opensuse/distribution/leap/15.5/repo/non-oss/ openSUSE-15.5-Non-Oss …...

第一篇:编写 Hello World 程序
编写 Hello World 程序 Hello World 程序就是让应用程序显示 Hello World 字符串。这是最简单的应用,但却包含了一个应用程序的基本要素,所以一般使用它来演示程序的创建过程。本章要讲的就是在Qt Creator 中创建一个图形用户界面的项目,从而…...

python 打印沁园春 雪 居中对齐 文本对齐
以下是python 中使用 DebugInfo 模块居中对齐打印《沁园春・雪》的效果 引入模块 pip install DebugInfopython代码 # -*- coding:UTF-8 -*-# region 引入必要依赖 from DebugInfo.DebugInfo import * # endregion诗文 沁园春 雪 作者: 毛主席 北国风光,千里冰封…...
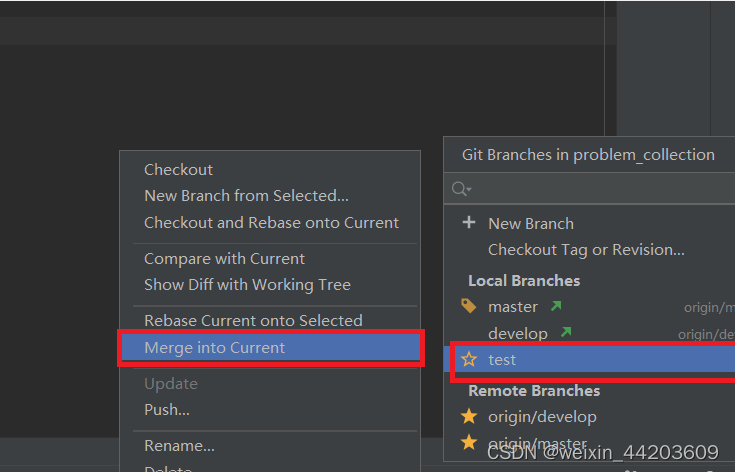
在 IDEA 中使用 Git开发 图文教程
在 IDEA 中使用 Git开发 图文教程 一、连接远程仓库二、IDEA利用Git进行开发操作三、分支操作3.1 新建分支3.2 切换分支3.3 删除分支3.4 比较分支3.5 合并分支 四、常用快捷键 一、连接远程仓库 一、打开IDEA,进入目录:File ->New ->Project from…...
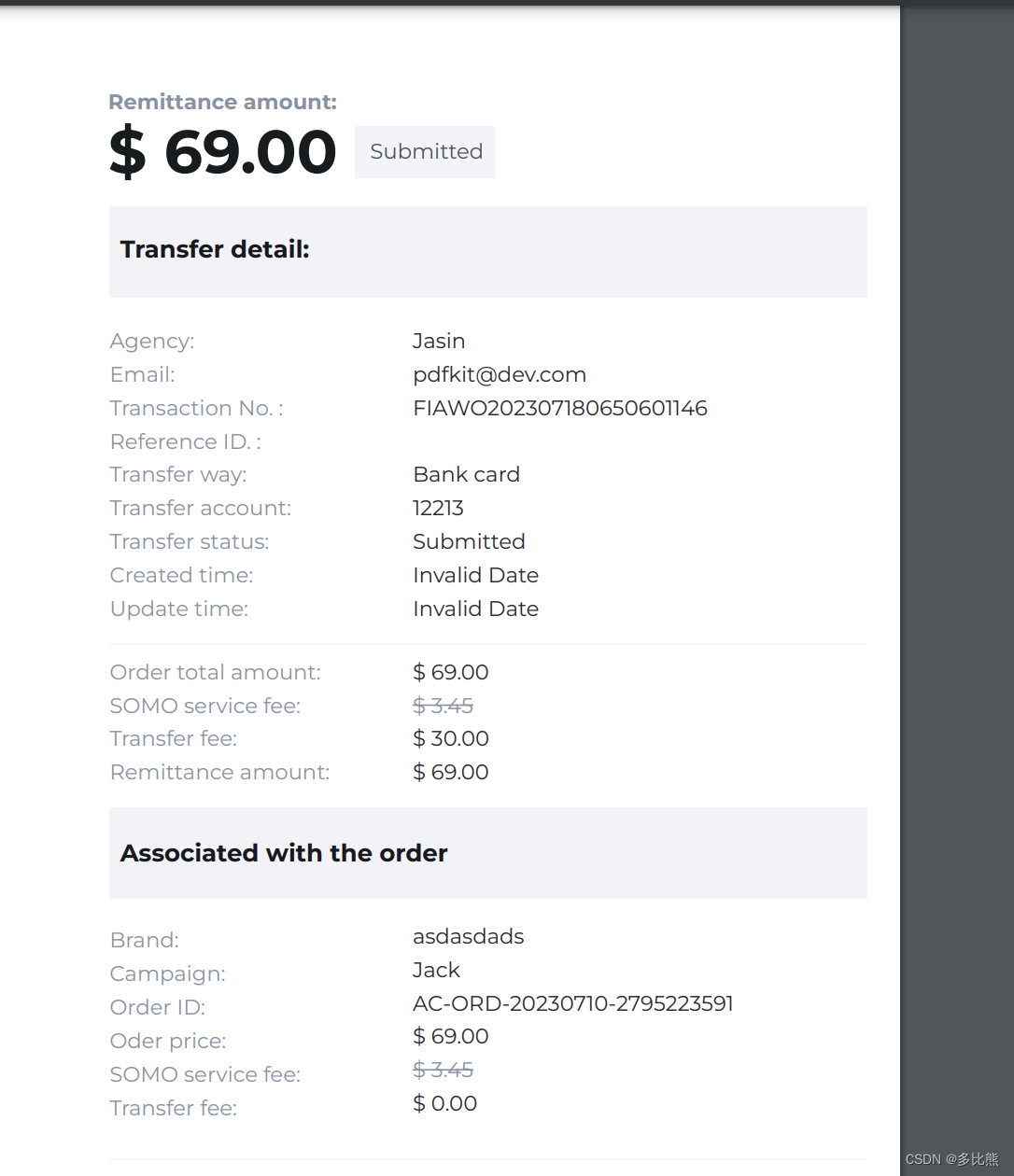
NodeJs导出PDF
(优于别人,并不高贵,真正的高贵应该是优于过去的自己。——海明威) 场景 根据订单参数生成账单PDF 结果 示例代码 /* eslint-disable no-unused-vars */ /* eslint-disable no-undef */ /* eslint-disable complexity */ const…...
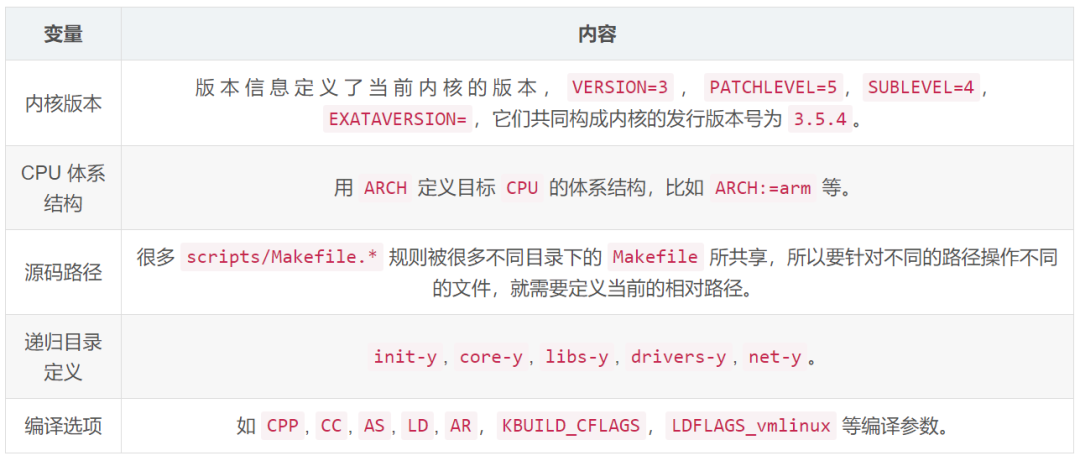
内核编译机制
inux内核的编译主要过程:配置、编译、安装。 配置主要由Kconfig提供图形界面完成 编译主要基于Kbuild编译系统,执行make完成编译 安装主要也是基于Kbuild提供的脚本,然后执行make完成安装 Kconfig Kconfig用于内核的配置,mak…...
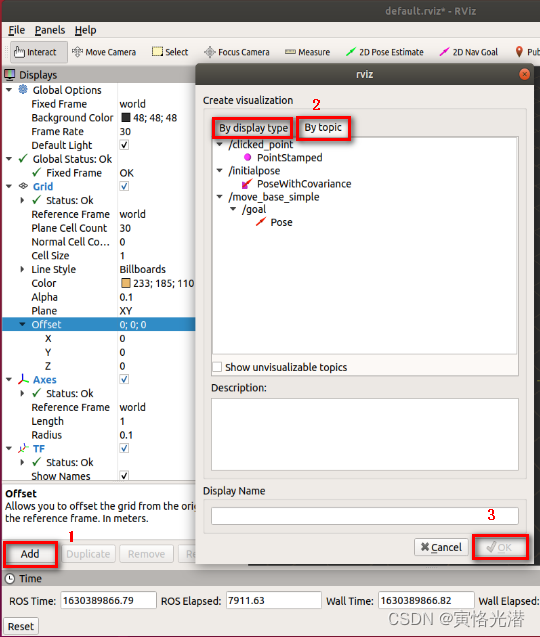
机器人TF坐标系变换与一些可视化工具的应用
TF坐标在ROS中是一个非常重要的概念,因为机器人在做日常操作任务的时候,对于其所在位置和朝向是需要时刻知道的,而机器人是由很多节点组成的协同任务,对于每个部件,我们需要知道它的位姿(位置和朝向),这使得…...
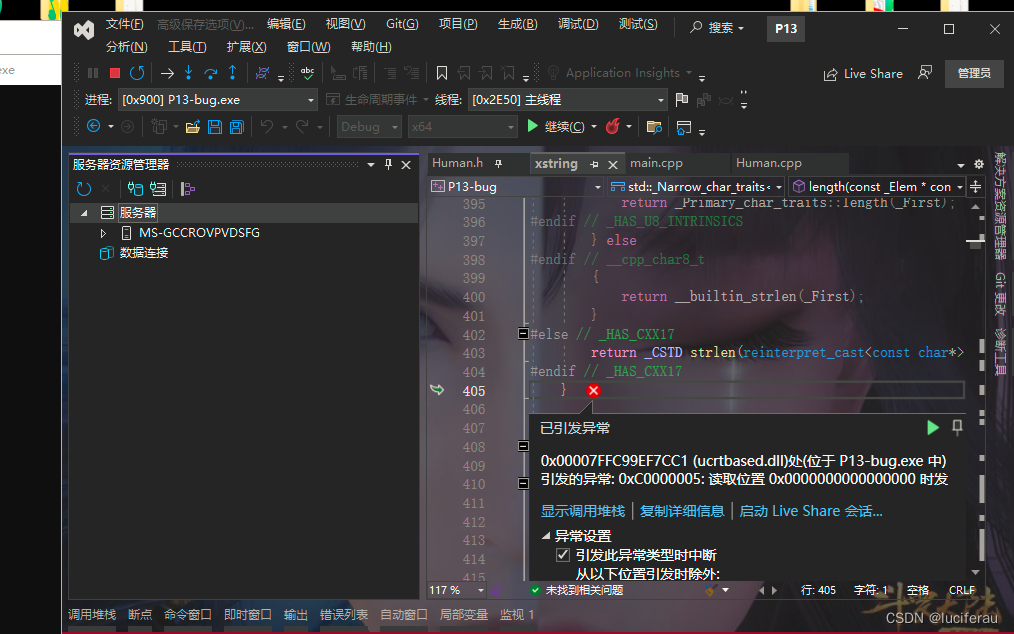
c++ 友元 运算符重载详解
友元 c是面向对象的,目的之一:封装 封装: 优点之一,就是安全。 缺点:在某些特殊的场合,不是很方便。 华为与IBM 40亿的咨询故事 IBM需要对华为各级部门做深度咨询分析, 为了提高咨询效率&a…...
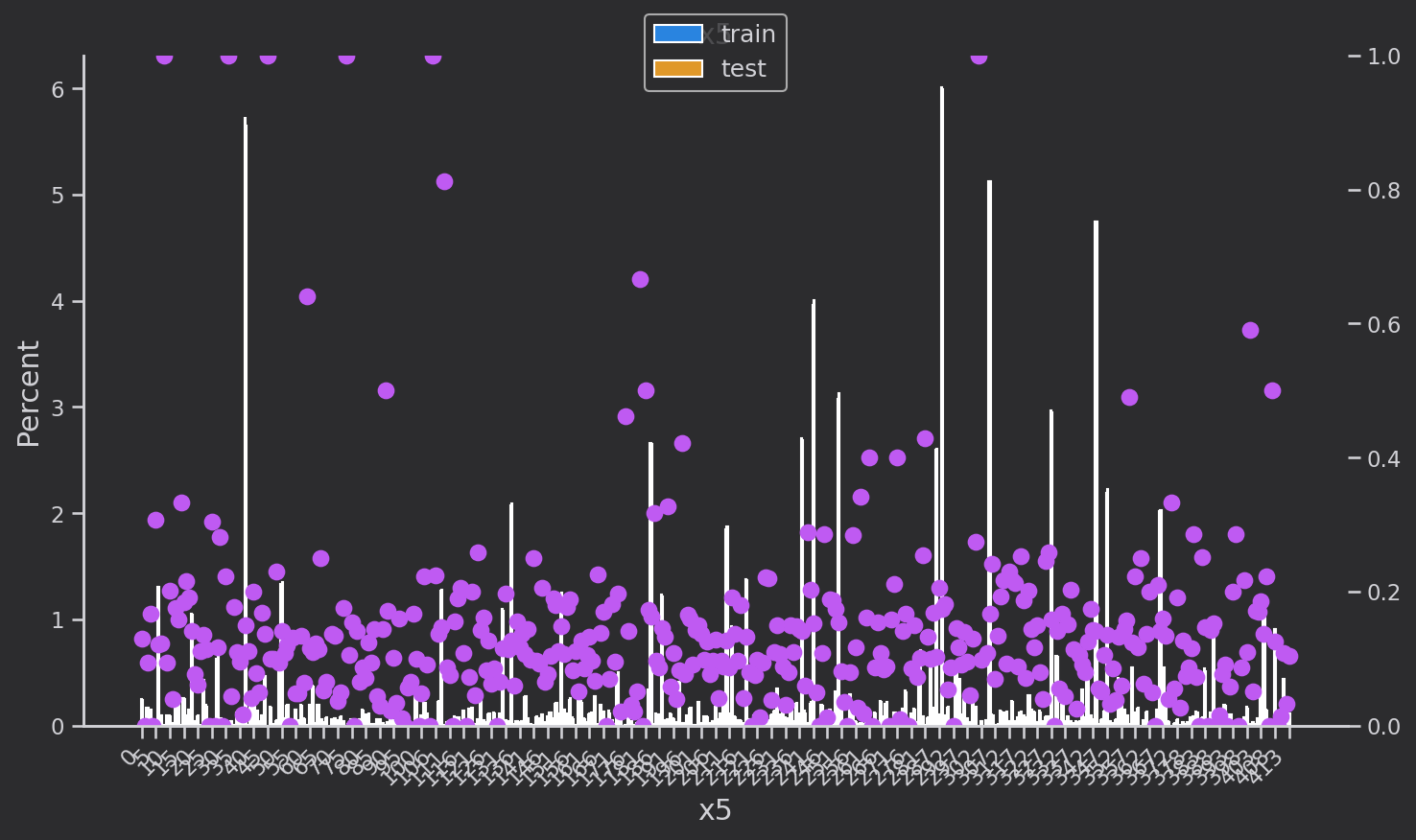
DataWhale 机器学习夏令营第三期
DataWhale 机器学习夏令营第二期 学习记录一 (2023.08.18)1.赛题理解2.缺失值分析3. 简单特征提取4. 数据可视化离散变量离散变量分布分析 DataWhale 机器学习夏令营第三期 ——用户新增预测挑战赛 学习记录一 (2023.08.18) 已跑通baseline,换为lightgbm基线&#…...

回归预测 | MATLAB实现BES-LSSVM秃鹰搜索算法优化最小二乘支持向量机多输入单输出回归预测(多指标,多图)
回归预测 | MATLAB实现BES-LSSVM秃鹰搜索算法优化最小二乘支持向量机多输入单输出回归预测(多指标,多图) 目录 回归预测 | MATLAB实现BES-LSSVM秃鹰搜索算法优化最小二乘支持向量机多输入单输出回归预测(多指标,多图&a…...
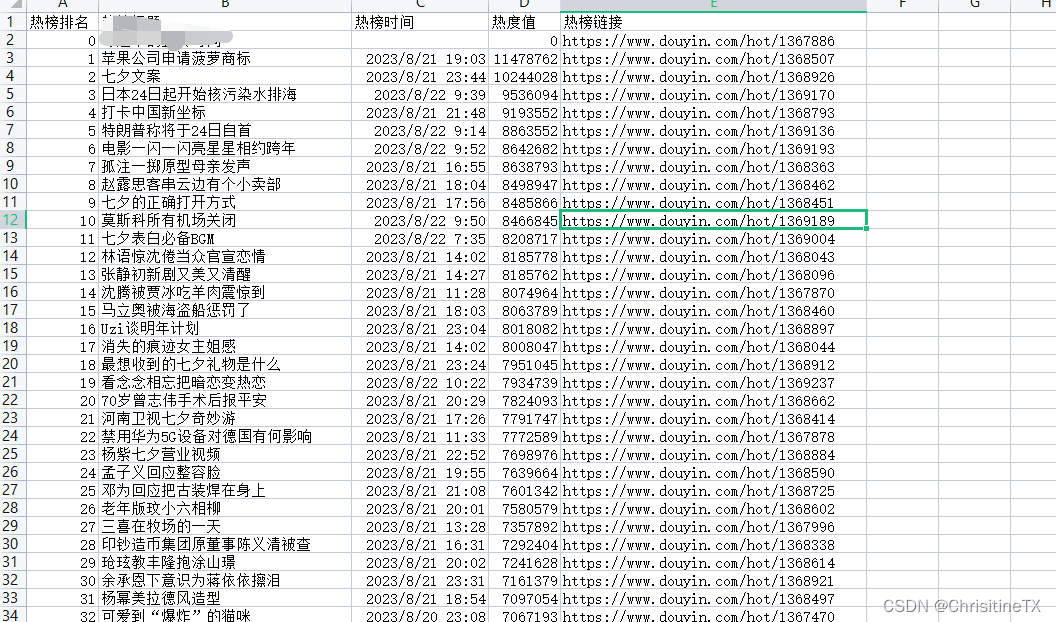
python分析实战(4)--获取某音热榜
1. 分析需求 打开某音热搜,选择需要获取的热榜如图 查找包含热搜内容的接口返回如图 将url地址保存 2. 开发 定义请求头 headers {Cookie: 自己的cookie,Accept: application/json, text/plain, */*,Accept-Encoding: gzip, deflate,Host: www.douyin.com,…...

Java根据List集合中的一个字段对集合进行去重
利用HashSet 创建了一个HashSet用于存储唯一的字段值,并创建了一个新的列表uniqueList用于存储去重后的对象。遍历原始列表时,如果字段值未在HashSet中出现过,则将其添加到HashSet和uniqueList中。 List<Person> originalList new Ar…...
)
(AtCoder Beginner Contest 315)
A.直接模拟即可 import random import sys import os import math from collections import Counter, defaultdict, deque from functools import lru_cache, reduce from itertools import accumulate, combinations, permutations from heapq import nsmallest, nlargest, h…...
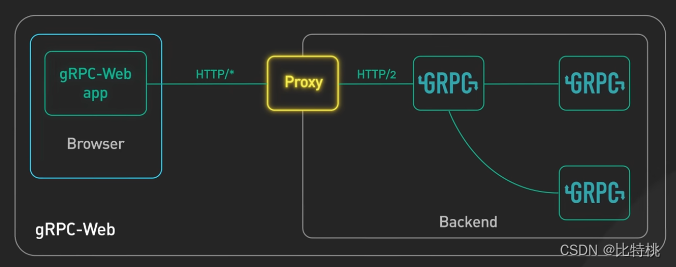
API 接口选择那个?RESTful、GraphQL、gRPC、WebSocket、Webhook
大家好,我是比特桃。目前我们的生活紧紧地被大量互联网服务所包围,互联网上每天都有数百亿次API调用。API 是两个设备相互通讯的一种方式,人们在手机上每次指尖的悦动,背后都是 API 接口的调用。 本文将列举常见的一些 API 接口&…...
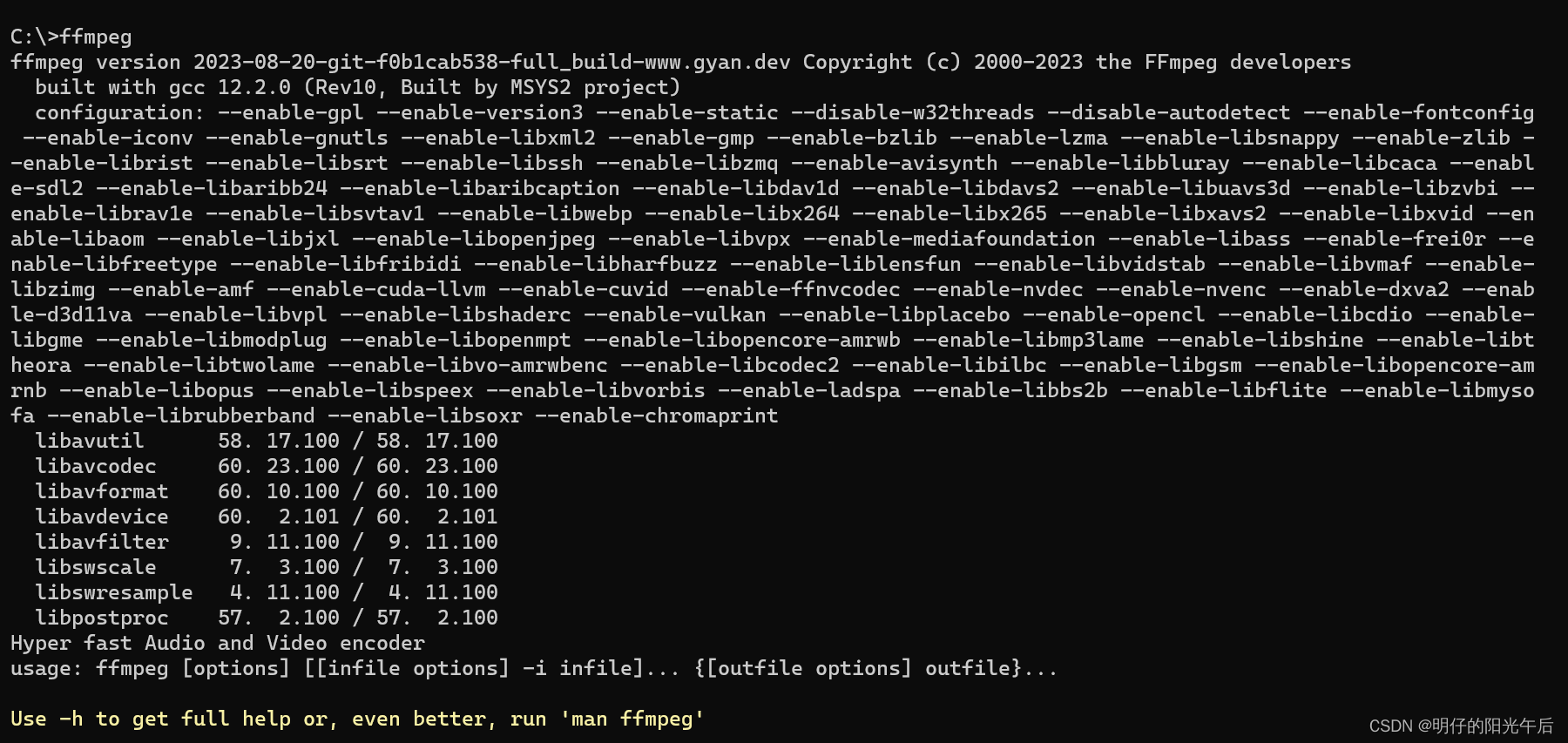
「Python|音视频处理|环境准备」如何在Windows系统下安装并配置音视频处理工具FFmpeg
本文主要介绍如何在Windows系统下安装并配置音视频处理工具FFmpeg,方便使用python进行音视频相关的下载或编辑处理。 文章目录 一、下载软件二、解压并配置三、验证安装 一、下载软件 首先要去 ffmpeg官网 下载软件包 由于上面直接下载的按钮是.tar.xz格式的。为了…...
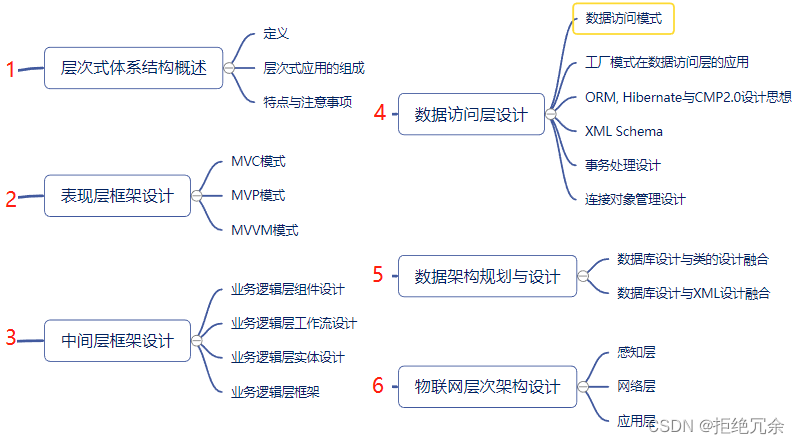
软考高级架构师下篇-12层次式架构设计理论与实践
目录 1. 考情分析2. 层次式体系结构概述3. 表现层框架设计4. 中间层框架设计5. 数据访问层设计6. 数据架构规划与设计7. 物联网层次架构设计8. 前文回顾1. 考情分析 根据考试大纲,层次式架构设计理论与实践知识点会涉及单选题型(约占2~5分)和案例题(25分),本小时内容偏重于方…...

234. 回文链表
234. 回文链表 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* L…...
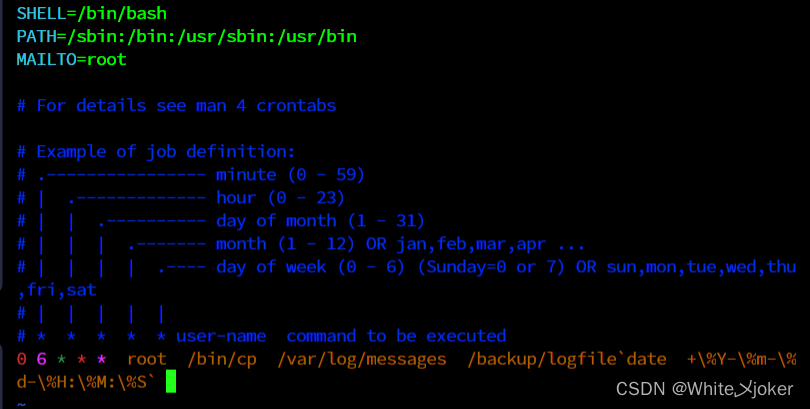
LInux之例行工作
目录 场景 单一执行例行任务 --- at(一次性) 安装 命令详解 语法格式 参数及作用 时间格式 案例 at命令执行过程分析 循环执行的例行性任务--crontab(周期性) crontd服务安装 linux 任务调度的工分类 crontab工作过程…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
