【数据结构】二叉树-堆实现及其堆的应用(堆排序topK问题)
文章目录
- 一、堆的概念及结构
- 二、堆的实现
- 1.结构的定义
- 2.堆的初始化
- 3.堆的插入
- 4.堆的向上调整
- 5.堆的删除
- 6.堆的向下调整
- 7.取出堆顶元素
- 8.返回堆的元素个数
- 9.判断堆是否为空
- 10.打印堆中的数据
- 11.堆的销毁
- 三、完整代码
- 1.Heap.h
- 2.Heap.c
- 3.test.c
- 四、堆排序
- 1.堆排序
- 2.建堆
- 3.选数
- 4.完整代码
- 五、topK问题
一、堆的概念及结构
如果有一个关键码的集合K = {k0,k1,k2…kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K 2*i+1 且Ki <= K2*i+2(Ki >= K2*i+1 且 Ki >= K2*i+2),i = 0,1,2…则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值
堆总是一棵完全二叉树
二、堆的实现
1.结构的定义
由于堆的元素是按完全二叉树的顺序存储方式存储在一个数组中,所以堆的结构和顺序表的结构一样
ypedef int HPDataType; //数据类型重定义typedef struct Heap
{HPDataType* a; //指向动态开辟的数组int size; //记录数组元素是个数int capacity; //记录容量,容量满时扩容
}HP;
2.堆的初始化
堆的初始化和顺序表的初始化方式一样,我们可以先开辟一块空间也可以不开辟,在插入数据的时候进行开辟,我们这里先不开辟空间
//初始化堆
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}
3.堆的插入
堆的插入我们需要注意两个地方:
1.由于堆只会在数组的尾部插入数据,所以我们不需要将CheckCapacity(检查容量)单独封装一个函数
2.由于我们在插入数据之后要保持堆的形态(大根堆或小根堆),所以我们需要对堆进行向上调整(调整数组里的数据,使其保持堆的形态),向上调整的过程其实也是建堆的过程
//堆的插入 -- 插入x继续保持堆形态
void HeapPush(HP* php, HPDataType x)
{assert(php);//堆为空或堆满时需要扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}//插入元素php->a[php->size] = x;php->size++;//向上调整堆,使其继续保持堆的形态AdjustUp(php->a, php->size - 1);
}4.堆的向上调整
这里我们以小根堆为例,如图,假设现在我们已经有了一个小根堆,现在我们在数组的最后(堆尾)插入一个数据,那么就可能出现两种情况:

1.插入的数据大于父亲节点,此时我们的堆仍然保存小根堆的结构,所以不需要进行调整,比如我们在上面的堆中插入30:

2.插入的数据小于父亲节点,这时我们就需要进行向上调整,直到根节点的大小小于父亲节点的大小(即小根堆),调整的次数由节点的大小决定,可能调整1次,也可能调整到根节点,比如我们插入10:

//交换两个节点
void Swap(HPDataType* p1, HPDataType* p2)
{assert(p1 && p2);HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//堆的向上调整 --小根堆
void AdjustUp(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2; //找到父节点//while (parent >= 0) 当父亲为0时,(0 - 1) / 2 = 0;又会进入循环while (child > 0) //当调整到跟节点的时候不再继续调整{//当子节点小于父节点的时候交换if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//迭代child = parent;parent = (child - 1) / 2;}//否则直接跳出循环else{break;}}
}
对于上面的代码我们需要注意循环结束的条件,如果我们使用parent >= 0这个来判断结束时,当父亲为0时,(0 - 1) / 2 = 0;又会进入循环,所以我们选择以孩子节点作为结束的条件:child > 0
【注意】如果我们需要建大根堆,只需要把交换的条件修改一下即可:
//当子节点小于父节点的时候交换
if (a[child] > a[parent])
5.堆的删除
对于堆的删除有明确的规定,我们只能删除堆顶的元素,但是顺序表头删又存在下面两个问题:
1.顺序表头删需要挪动数据,效率低下O(N)
2.头删之后堆中各节点的父子关系全被破坏了
对于上面的两个问题,我们采用如下的解决方案:
1.我们在删除之前先将堆顶的元素和堆尾的元素进行交换,然后–size(删除数组的最后一个元素/堆尾元素),这个月就相当于删除了堆顶的元素,并且时间复杂度从O(N)提升到了O(1)
2.由于我们把堆尾的元素交换到了堆顶,堆的结构被破坏,所以我们需要设计一个向下调整的算法来继续保持堆的形态:
//删除堆顶元素 --找次大或者次小 -- logN
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));//首先交换堆顶和堆尾的元素Swap(&php->a[0], &php->a[php->size - 1]);//删除堆顶的元素php->size--;//向下调整,保持堆的形态AdjustDown(php->a, php->size, 0);
}
6.堆的向下调整
堆的向下调整和堆的向下调整刚好相反,我们以小根堆为例,我们调整的思路如下:1.找出子节点中较小的节点;
2.比较父节点和较小节点的大小,如果父节点比子节点大就交换两个节点,反之说明现在的形态已经是堆,不需要进行调整了;3.交换之后,原来的子节点称为新的父节点,然后继续执行1,2步骤,直到调整为堆的结构:

//堆的向下调整 --小根堆
void AdjustDown(HPDataType* a, int n, int parent)
{assert(a);int minchild = parent * 2 + 1;while (minchild < n){//找出那个较小的孩子if (a[minchild] > a[minchild + 1] && minchild + 1 < n){minchild++;}//当子节点小于父节点的时候交换if (a[minchild] < a[parent]){Swap(&a[minchild], &a[parent]);//迭代parent = minchild;minchild = parent * 2 + 1;}else{break;}}
}
和向上调整类似,如果我们想要调整为大堆,也只需要改变交换条件即可:
// 找出较大的节点
if (a[maxchild] > a[maxchild + 1] && axchild + 1 < n)
// 如果父节点小于子节点就交换
if (a[maxchild] > a[parent])
7.取出堆顶元素
堆顶元素就是数组的第一个元素
//获取堆顶的元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
8.返回堆的元素个数
/返回堆的元素个数
int HeapSize(HP* php)
{assert(php);return php->size;
}
9.判断堆是否为空
//判断堆是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
10.打印堆中的数据
//打印堆中的数据
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}
11.堆的销毁
//堆的销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}
三、完整代码
1.Heap.h
#pragma once //防止头文件被重复包含//包含头文件
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>typedef int HPDataType; //数据类型重定义typedef struct Heap
{HPDataType* a; //指向动态开辟的数字int size; //记录数组元素是个数int capacity; //记录容量,容量满时扩容
}HP;//初始化堆
void HeapInit(HP* php);
//堆的销毁
void HeapDestroy(HP* php);
//堆的插入
void HeapPush(HP* php, HPDataType x);
//堆的向上调整
void AdjustUp(HPDataType* a, int child);
//删除堆顶元素
void HeapPop(HP* php);
//堆的向下调整
void AdjustDown(HPDataType* a, int n, int parent);
//获取堆顶的元素
HPDataType HeapTop(HP* php);
//判断堆是否为空
bool HeapEmpty(HP* php);
//返回堆的元素个数
int HeapSize(HP* php);
//打印堆中的数据
void HeapPrint(HP* php);
2.Heap.c
#include "Heap.h"//初始化堆
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//堆的销毁
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}//堆的插入 -- 插入x继续保持堆形态
void HeapPush(HP* php, HPDataType x)
{assert(php);//堆为空或堆满时需要扩容if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}//插入元素php->a[php->size] = x;php->size++;//向上调整堆,使其继续保持堆的形态AdjustUp(php->a, php->size - 1);
}//交换两个节点
void Swap(HPDataType* p1, HPDataType* p2)
{assert(p1 && p2);HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//堆的向上调整 --小根堆
void AdjustUp(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2; //找到父节点//while (parent >= 0) 当父亲为0时,(0 - 1) / 2 = 0;又会进入循环while (child > 0) //当调整到跟节点的时候不再继续调整{//当子节点小于父节点的时候交换if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//迭代child = parent;parent = (child - 1) / 2;}//否则跳出循环else{break;}}
}
//删除堆顶元素 --找次大或者次小 -- logN
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));//首先交换堆顶和堆为的元素Swap(&php->a[0], &php->a[php->size - 1]);//删除堆顶的元素php->size--;//向下调整,保持堆的形态AdjustDown(php->a, php->size, 0);
}//堆的向下调整 --小根堆
void AdjustDown(HPDataType* a, int n, int parent)
{assert(a);int minchild = parent * 2 + 1;while (minchild < n){//找出那个较小的孩子if (a[minchild] > a[minchild + 1] && minchild + 1 < n){minchild++;}//当子节点小于父节点的时候交换if (a[minchild] < a[parent]){Swap(&a[minchild], &a[parent]);//迭代parent = minchild;minchild = parent * 2 + 1;}else{break;}}
}
//获取堆顶的元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
//判断堆是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
//返回堆的元素个数
int HeapSize(HP* php)
{assert(php);return php->size;
}
//打印堆中的数据
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}
3.test.c
#include "Heap.h"int main()
{int a[10] = { 15, 18, 19, 25, 28, 34, 65, 49, 27, 37 };HP hp;//初始化堆HeapInit(&hp);//建堆for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++){HeapPush(&hp, a[i]);}//插入元素HeapPush(&hp, 10);HeapPrint(&hp);//删除堆顶元素HeapPop(&hp);HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);//打印堆的元素while (!HeapEmpty(&hp)){printf("%d ", HeapTop(&hp));HeapPop(&hp);}printf("\n");return 0;
}
【总结】
1.堆是二叉树顺序存储结构的一个具体体现,堆中的每个节点的值总是不大于或不小于父节点的值(大堆/小堆),堆总是一棵完全二叉树,堆使用顺序表进行存储
2.堆中父节点下标的计算公式:(n-1)/2;左孩子下标:n*2+1;右孩子下标:n*2+2;
3.堆只能在尾部插入数据,且插入数据后需要保证堆的结构,所以在插入数据之后我们需要进行向上调整,向上调整的时间复杂度为O(logN)(log以2为底)
4.堆只能在头部删除数据,且删除数据后需要保证堆的结构,又因为顺序表在头部删除数据需要挪动数据,效率很低而且会破坏堆的结构,所以在堆删除数据时会先将堆尾的数据和堆顶的数据进行交换,然后–size(删除数组最后一个元素/队尾元素),再进行向下调整,向下调整的时间复杂度为O(logN)(log以2为底)
四、堆排序
1.堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。时间复杂度:O(N*logN)空间复杂度:O(1)
2.建堆
堆排序的第一步就是建堆,建堆有两种方法:向上调整建堆和向下调整建堆
**向下调整建堆:**从最后一个非叶子节点(即最后一个叶子节点的父节点)开始向下调整,直到调整到根节点



向下调整建堆的时间复杂度:

调整次数 = 每一层节点个数 * 这一层节点最坏向下调整次数
T(N) = 2^0*(h-1) + 2^1*(h-2) + 2^2*(h-3) + 2^3*(h-4) + …+2^(h-2)*1
错位相减法:
2*T(N) = 2^1*(h-1) + 2^2*(h-2) + 2^3*(h-3) + … + 2^(h-2)*2 + 2^(h-1)*1
T(N) = 2^0*(h-1) + 2^1*(h-2) + 2^2*(h-3) + 2^3*(h-4) + …+2^(h-2)*1
两式相减得:
T(N) = -2^0*(h-1) + 2^1 + 2^2 + … +2^(h-2) + 2^(h-1)
T(N) = -h + 2^0 + 2^1 + 2^2 + … +2^(h-2) + 2^(h-1)
T(N) = -h + 2^h-1
高度为h,节点数量为N的完全二叉树,2^h-1=N,h = log(N+1)(log以2为底)
T(N) = N - log(N+1)(log以2为底)
所以,向下调整建堆的时间复杂度为O(N)
**向上调整建堆:**把数组的第一个元素作为堆的根节点,然后在堆尾一次插入其余元素,每插入一个元素就向上调整一次,从而保证堆的结构:

**向上调整建堆的时间复杂度:**由于堆的完全二叉树,而满二叉树又是完全二叉树的一种,所以此处为了简化计算,使用满二叉树来计算时间复杂度(时间复杂度本身看来就是近似值,多几个节点不影响最终结果)

我们知道:调整次数 = 每一层节点个数 * 这一层节点最坏向下调整次数
T(N) = 2^1*1 + 2^2*2 + 2^3*3 + …2^(h-2)*(h-2) + 2^(h-1)*(h-1)
精确算,还是用错位相减法
高度为h,节点数量为N的完全二叉树,2^h-1=N,h = log(N+1)(log以2为底)
算大概就算最后一层:2^(h-1)*(h-1)
2^(h-1)*(h-1) * 2/2
2^h*(h-1)/2
(N+1)*(log(N+1))/2
所以向上调整的时间复杂度为O(N*logN)
综合上面两种建堆的方式,我们选择向下调整建堆,所以建堆的时间复杂度为O(N);
3.选数
现在我们已经完成了建堆,那么接下来就需要进行选数,假设我们需要排升序,那么方法一共有三种:
1.建小堆,开辟一个和原数组同等大小的新数组中,每次取出堆顶元素(最小元素)放在新的数组中,然后挪动数组中的数据,最后排好序了以后再将新数组的数据覆盖到原数组;
缺点:每次挪动数据的效率很低,且挪动数据会造成堆中的其余元素的父子关系混乱,需要重新建堆,而建堆的时间复杂度也是O(N),所以排N个数,时间复杂度为O(N*N),空间复杂度为O(N)
2.建小堆,我们借鉴Pop数据的方法,先将堆顶的元素放在新的数组中,然后交换堆顶和队尾的元素,然后进行向下调数组的前n-1个数据,直到排好序,最后将新数组中的元素覆盖到原数组中;
缺点:虽然此方法可以让我们每次都拿到数组中最小的元素,但是需要开辟额外的空间,时间复杂度为O(N*lonN),空间复杂度为O(N)
3.建大堆,先将堆顶和队尾的数据进行交换,使得数组中最大的元素处于数组的末尾,然后向下调整前n-1个元素,使得次大的数据位于堆顶,然后重复前面的步骤,把次大的数据存放到最大的数据之前,直到数组有序;
优点:没有额外的空间消耗,且效率达到了O(N*logN)
综合上面的三种选数的方法:选数的时间复杂度为O(N*logN),空间复杂度为O(N)
4.完整代码
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>
#include <assert.h>//空间复杂度O(1)
//时间复杂度O(N*logN)typedef int HPDataType;
//交换两个节点
void Swap(HPDataType* p1, HPDataType* p2)
{assert(p1 && p2);HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//堆的向上调整 --小根堆
void AdjustUp(HPDataType* a, int child)
{assert(a);int parent = (child - 1) / 2; //找到父节点//while (parent >= 0) 当父亲为0时,(0 - 1) / 2 = 0;又会进入循环while (child > 0) //当调整到跟节点的时候不再继续调整{//当子节点小于父节点的时候交换//if (a[child] > a[parent]) 大根堆if (a[child] < a[parent]){Swap(&a[child], &a[parent]);//迭代child = parent;parent = (child - 1) / 2;}//否则跳出循环else{break;}}
}//堆的向下调整 --小根堆
void AdjustDown(HPDataType* a, int n, int parent)
{assert(a);int minchild = parent * 2 + 1;while (minchild < n){//找出那个较小的孩子if (a[minchild] > a[minchild + 1] && minchild + 1 < n){minchild++;}//if (a[minchild] > a[parent]) 大根堆//当子节点小于父节点的时候交换if (a[minchild] < a[parent]){Swap(&a[minchild], &a[parent]);//迭代parent = minchild;minchild = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* a, int n)
{/* 建堆 -- 向上调整建堆 - O(N*logN)for (int i = 1; i < n; ++i){AdjustUp(a, i);}*/// 大思路:选择排序,依次选数,从后往前排// 升序 -- 大堆// 降序 -- 小堆//建堆 -- 向下调整建堆 - O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}int i = 1;while (i < n){Swap(&a[0], &a[n - i]); // 交换堆尾和堆顶的数据AdjustDown(a, n - i, 0); //向下调整++i;}
}int main()
{int a[] = { 15, 1, 19, 25, 8, 34, 65, 4, 27, 7 };HeapSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}printf("\n");return 0;
}

五、topK问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大,比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。
N个数,找前K个最大的,如何处理?
1.排序 --O(N*logN)
2.堆选数
(1)建大堆:建N个数的大堆,选K次即可(Pop K次) O(N)+O(N*logK)
(2)建小堆:假设N很大,K很小,比如N=100亿,K=100,那么(1)方法就不行了
N很大的时候,内存就存不下了,就只能存在磁盘中
100亿整数=40G
400亿Byte
1G=1024MB
1024MB=1024*1024KB
1024*1024KB=1024*1024*1024Byte
时间复杂度为O(K)+O(logK*(N-K)) 空间复杂度 O(K)
思路:前K个数,建K个数的小堆,依次遍历后续N-K个数,比堆顶的数据大,就替换堆顶数据,向下调整建堆
最佳的方式就是用堆来解决,基本思路如下:
第一步,用数据集合中的前K个元素来建堆–前K个最大元素,则建小堆,前K个最小元素,则建大堆;
第二步,用剩余的N-K个元素依次与堆顶的元素进行比较,前K大的元素,则大于堆顶元素则就替换堆顶数据,进行向下调整前K小的元素,则小于堆顶的元素替换堆顶数据,进行向下调整;
#include <stdio.h>
#include <stdlib.h>// 交换两个节点
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 向下调整 --建小堆
void AdjustDown(int a[], int n, int parent)
{int minchild = parent * 2 + 1; // 找到左孩子(左孩子 + 1得到右孩子)while (minchild < n) // 调整到数组尾时不在调整{if (minchild + 1 < n && a[minchild + 1] < a[minchild]){minchild += 1;}if (a[parent] > a[minchild]){Swap(&a[parent], &a[minchild]);}else{break;}}// 迭代parent = minchild;minchild = parent * 2 + 1;
}int* TopK(int* a, int n, int k)
{// 开辟K个元素的空间int* minHeap = (int*)malloc(sizeof(int) * k);if (minHeap == NULL){perror("malloc fail");return NULL;}// 将数组的前K个元素for (int i = 0; i < k; i++){minHeap[i] = a[i];}// 建小堆 --向下调整建堆:O(N)// n-1找到最后一个叶子节点,该节点-1/2找到倒数第一个父节点for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(minHeap, k, i);}// 取N-K个元素与堆顶元素比较,如果大于堆顶元素,就如堆for (int i = k; i < n; i++){if (minHeap[0] < a[i]){minHeap[0] = a[i];AdjustDown(minHeap, k, 0);}}return minHeap;
}int main()
{int arr[] = { 15,1,19,25,8,34,65,4,27,7 };int n = sizeof(arr) / sizeof(arr[0]);// TopK问题--前K个最大的元素int k = 3;int* ret = TopK(arr, n, k);for (int i = 0; i < k; i++){printf("%d ", ret[i]);}free(ret);ret = NULL;return 0;
}
```c;minchild = parent * 2 + 1;
}int* TopK(int* a, int n, int k)
{// 开辟K个元素的空间int* minHeap = (int*)malloc(sizeof(int) * k);if (minHeap == NULL){perror("malloc fail");return NULL;}// 将数组的前K个元素for (int i = 0; i < k; i++){minHeap[i] = a[i];}// 建小堆 --向下调整建堆:O(N)// n-1找到最后一个叶子节点,该节点-1/2找到倒数第一个父节点for (int i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(minHeap, k, i);}// 取N-K个元素与堆顶元素比较,如果大于堆顶元素,就如堆for (int i = k; i < n; i++){if (minHeap[0] < a[i]){minHeap[0] = a[i];AdjustDown(minHeap, k, 0);}}return minHeap;
}int main()
{int arr[] = { 15,1,19,25,8,34,65,4,27,7 };int n = sizeof(arr) / sizeof(arr[0]);// TopK问题--前K个最大的元素int k = 3;int* ret = TopK(arr, n, k);for (int i = 0; i < k; i++){printf("%d ", ret[i]);}free(ret);ret = NULL;return 0;
}
相关文章:

【数据结构】二叉树-堆实现及其堆的应用(堆排序topK问题)
文章目录一、堆的概念及结构二、堆的实现1.结构的定义2.堆的初始化3.堆的插入4.堆的向上调整5.堆的删除6.堆的向下调整7.取出堆顶元素8.返回堆的元素个数9.判断堆是否为空10.打印堆中的数据11.堆的销毁三、完整代码1.Heap.h2.Heap.c3.test.c四、堆排序1.堆排序2.建堆3.选数4.完…...

ubuntu Repo 安装
//进入repo临时下载存放目录 cd Downloads //下载repo(从清华镜像网站) curl https://mirrors.tuna.tsinghua.edu.cn/git/git-repo -o repo //创建repo执行目录 mkdir ~/.bin //copy repo到上述目录 cp /home/xxx/Downloads/repo ~/.bin/ //添加执行权限…...

JAVA:选择排序算法及其编写
选择排序算法是一种比较经典的排序算法,与其类似的冒泡排序算法的思想有点不同,它采用的是选择第一个和后n-1个进行比较,将最小的排在第一个位置,后面的依此方式进行。 一、算法步骤 步骤1:初始化数组arry(假设其长度…...

【Linux】——基础开发工具和vim编辑器的基本使用方法
目录 Linux 软件包管理器 yum Linux编辑器-vim使用 1.vim的基本概念 2. vim的基本操作 3. vim正常模式命令集 4. vim末行模式命令集 如何配置vim Linux 软件包管理器 yum yum是Linux下的一个下载软件的软件 对于yum,现阶段只需要会使用yum的三板斧就…...

R语言部分题解
请论述大数据的四个特点 数据量大(Volume)、数据种类多(Variety)、数据价值密度低(Value)、数据增长速度快(Velocity) 为什么目前大数据被广泛使用 科技的进步、基础建设的改进、资料获取变轻松 计算1~10的平均数 mean(c(1,2,3,4,5,6,7,8,9,10))3~15…...
水文监测场景的数据通信规约解析和落地实践
[小 迪 导 读]:江苏云上需要通过云平台接入水文设备来实现水文数据的采集、存储、显示、控制、报警及传输等综合功能。企业介绍江苏云上智联物联科技有限公司是专业从事物联网相关产品与解决方案服务的高科技公司,总部位于美丽的江苏无锡。公司遵循“智联…...

【数据结构】时间复杂度和空间复杂度
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 小苏希望大家能从这篇文章中收获到许…...

从发现SQL注入到ssh连接
前言: 某天,同事扔了一个教育站点过来,里面的url看起来像有SQL注入。正好最近手痒痒,就直接开始。 一、发现时间盲注和源码 后面发现他发的url是不存在SQL注入的,但是我在其他地方发现了SQL盲注。然后改站点本身也可…...
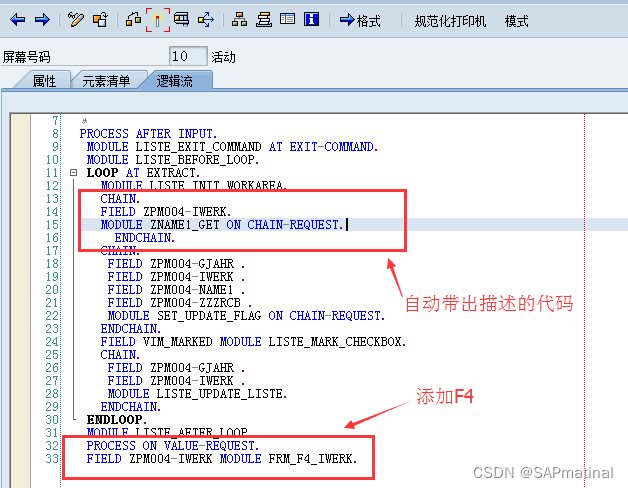
SAP ABAP
方法一: REPORT ZDCH_09_TEST2. ************************************************************************ * DATEN DEFINITION * *********************************************************************…...

C/C++每日一练(20230219)
目录 1. 用队列实现栈 2. 判断是否能组成三角形 3. 只出现一次的数字 II 附录 栈(Stack)和队列(Queue)的异同 1. 栈和队列的相同点 2. 栈和队列的不同点 1. 用队列实现栈 请你仅使用两个队列实现一个后入先出(…...

【NestJS】模块
脚手架中,可以执行 nest g mo XXX 创建模块。通过脚手架命令创建的模块,会自动被导入至根模块注册。 注意:项目中的模块都需要导入到根模块中注册一下才能被使用。 共享模块 nest g res boy、nest g res girl 如果希望在 girl 模块中使用 …...

隐私计算头条周刊(2.13-2.19)
开放隐私计算收录于合集#企业动态44个#周刊合辑44个#政策聚焦37个#隐私计算91个#行业研究36个开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播…...
【STM32笔记】低功耗模式配置及避坑汇总
【STM32笔记】低功耗模式配置及配置汇总 文章总结:(后续更新以相关文章为准) 【STM32笔记】__WFI();进入不了休眠的可能原因 【STM32笔记】HAL库低功耗模式配置(ADC唤醒无法使用、低功耗模式无法烧录解决方案&#x…...
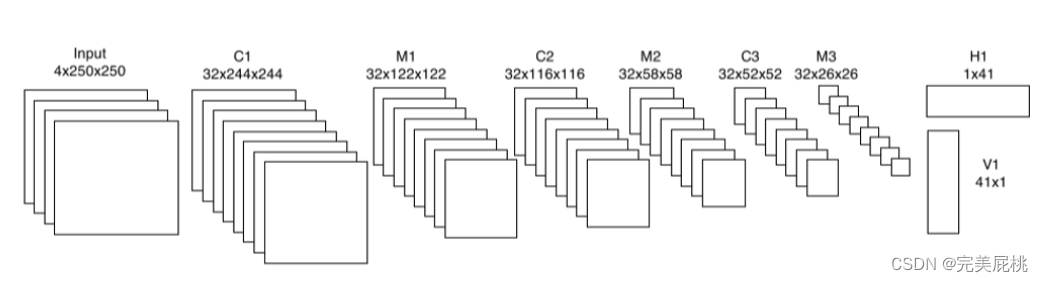
DFN: Dynamic Filter Networks-动态卷积网络
一、论文信息 论文名称:Dynamic Filter Networks 作者团队:NIPS2016 二、动机与创新 卷积层是通过将上一层的特征映射与一组过滤器进行卷积计算输出特征映射,滤波器是卷积层的唯一参数,通常用反向传播算法在训练中学习ÿ…...
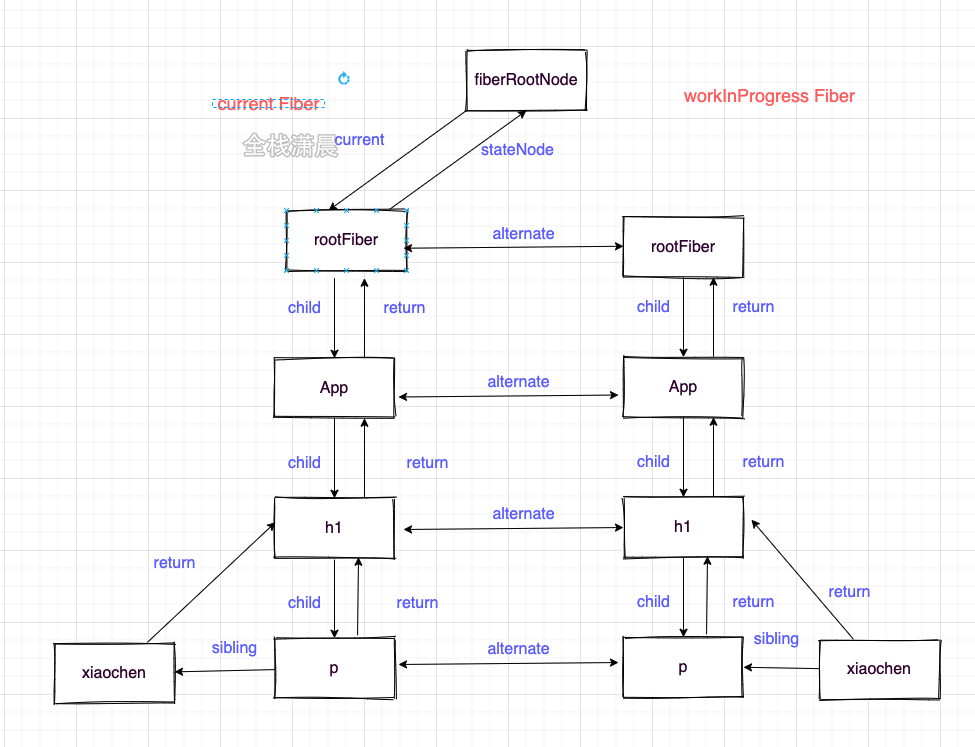
面试官:你是怎样理解Fiber的
hello,这里是潇晨,今天我们来聊一聊Fiber。不知道大家面试的时候有没有遇到过和react Fiber相关的问题呢,这一类问题比较开放,但也是考察对react源码理解深度的问题,如果面试高级前端岗,恰巧你平时用的是re…...

【C++的OpenCV】第一课-opencv的介绍和安装(Linux环境下)
第一课-目录一、基本介绍1.1 官网1.2 git源码1.3 介绍二、OpenCV的相关部署工作2.1 Linux平台下部署OpenCV一、基本介绍 1.1 官网 opencv官网 注意:官网为英文版本,可以使用浏览器自带的翻译插件进行翻译,真心不推荐大家去看别人翻译的&am…...
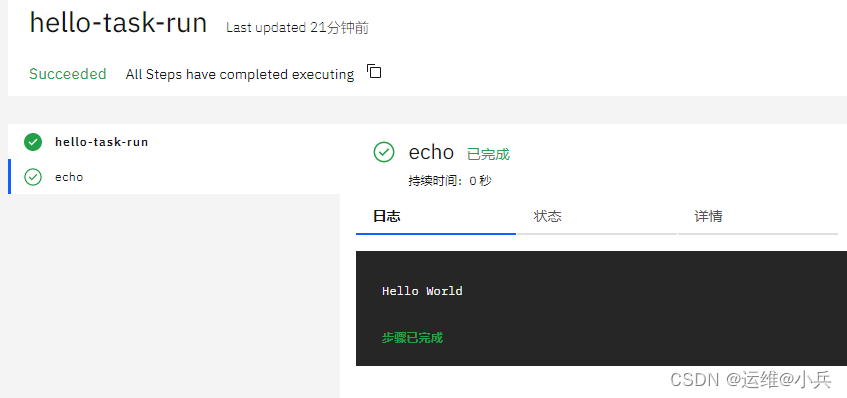
k8s安装tekton,编写task
文章目录一、官方安装二、国内资源安装安装tekton安装dashboard安装CLI三、demo编写task.yaml编写taskRun.yaml使用tkn命令查看参考文章一、官方安装 地址:https://tekton.dev/docs/installation/pipelines/#installing-tekton-pipelines-on-kubernetes 注意&#…...

K_A12_014 基于STM32等单片机驱动S12SD紫外线传感器模块 串口与OLED0.96双显示
K_A12_014 基于STM32等单片机驱动S12SD紫外线传感器模块 串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:数据对比:四、部分代码说明1、接线引脚定义1.1、STC89C52RCS12SD紫外线传感器模块1.2、STM32F103…...
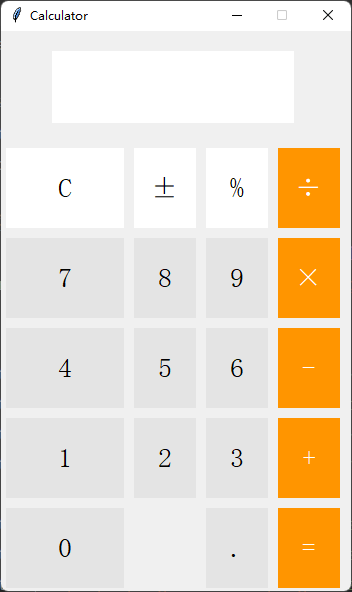
还真不错,今天 Chatgpt 教会我如何开发一款小工具开发(Python 代码实现)
上次使用 Chatgpt 写爬虫,虽然写出来的代码很多需要修改后才能运行,但Chatgpt提供的思路和框架都是没问题。 这次让 Chatgpt 写一写GUI程序,也就是你常看到的桌面图形程序。 由于第一次测试,就来个简单点的,用Python…...
Boom 3D最新版本下载电脑音频增强应用工具
为了更好地感受音乐的魅力,Boom 3D 可以让你对音效进行个性化增强,并集成 3D 环绕立体声效果,可以让你在使用任何耳机时,都拥有纯正、优质的音乐体验。Boom 3D是一款充满神奇魅力的3D环绕音效升级版,BOOM 3D是一个全新…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
