C/C++每日一练(20230219)

目录
1. 用队列实现栈
2. 判断是否能组成三角形
3. 只出现一次的数字 II
附录
栈(Stack)和队列(Queue)的异同
1. 栈和队列的相同点
2. 栈和队列的不同点
1. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x)将元素 x 压入栈顶。int pop()移除并返回栈顶元素。int top()返回栈顶元素。boolean empty()如果栈是空的,返回true;否则,返回false。
注意:
- 你只能使用队列的基本操作 —— 也就是
push to back、peek/pop from front、size和is empty这些操作。 - 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入: ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 2, 2, false]
解释: MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False
提示:
1 <= x <= 9- 最多调用
100次push、pop、top和empty - 每次调用
pop和top都保证栈不为空
进阶:你能否实现每种操作的均摊时间复杂度为 O(1) 的栈?换句话说,执行 n 个操作的总时间复杂度 O(n) ,尽管其中某个操作可能需要比其他操作更长的时间。你可以使用两个以上的队列。
代码:
#include <bits/stdc++.h>
using namespace std;
class MyStack
{
public:MyStack(){}void push(int x){std::queue<int> temp_queue;temp_queue.push(x);while (!_data.empty()){temp_queue.push(_data.front());_data.pop();}while (!temp_queue.empty()){_data.push(temp_queue.front());temp_queue.pop();}}int pop(){int x = _data.front();_data.pop();return x;}int top(){return _data.front();}bool empty(){return _data.empty();}
private:std::queue<int> _data;
};int main()
{MyStack myStack;myStack.push(1);myStack.push(2);cout << myStack.top() << endl;cout << myStack.pop() << endl;cout << myStack.empty() << endl;return 0;
}输出:
2
2
0
2. 判断是否能组成三角形
根据输入的三角形的三边判断是否能组成三角形,若可以则输出它的周长和三角的类型
代码:
#include<stdlib.h>
#include<stdio.h>int main(void)
{int num1,num2,num3;printf("请输入第一条边:");scanf("%d",&num1);printf("请输入第二条边:");scanf("%d",&num2);printf("请输入第三条边:");scanf("%d",&num3);if(num1+num2>num3&&num2+num3>num1&&num1+num3>num2){if (num1*num1+num2*num2==num3*num3||num2*num2+num3*num3==num1*num1||num1*num1+num3*num3==num2*num2){printf ( "%d、%d和%d可以组成直角三角形。",num1,num2,num3);printf ("\n三角形周长:%d\n",num1+num2+num3);}else if (num1*num1+num2*num2<num3*num3||num2*num2+num3*num3<num1*num1||num1*num1+num3*num3<num2*num2){printf ("%d、%d和%d可以组成钝角三角形。",num1,num2,num3);printf ("\n三角形周长:%d\n",num1+num2+num3);}else{printf ("%d、%d和%d可以组成锐角三角形",num1,num2,num3);printf ("\n三角形周长:%d\n",num1+num2+num3);}}elseprintf("%d, %d和%d不能组成三角形。",num1,num2,num3);system("PAUSE");return 0;
}输入输出:
请输入第一条边:3
请输入第二条边:3
请输入第三条边:3
3、3和3可以组成锐角三角形
三角形周长:9
请按任意键继续. . .
3. 只出现一次的数字 II
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
示例 1:
输入:nums = [2,2,3,2] 输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99] 输出:99
提示:
1 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1nums中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
进阶:你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
代码:
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:int singleNumber(vector<int> &nums){sort(nums.begin(), nums.end());int res = 0;int i = 0;for (int j = 1; j < nums.size(); j++){if (nums[j] != nums[i]){if (j - i == 1){res = nums[i];break;}else{i = j;}}}if (i == nums.size() - 1){res = nums[i];}return res;}
};int main()
{Solution s;vector <int> vect = {2,2,3,2};cout << s.singleNumber(vect) << endl;vect = {0,1,0,1,0,1,99};cout << s.singleNumber(vect) << endl; return 0;
}
输出:
3
99
附录
栈(Stack)和队列(Queue)的异同
线性表:线性表是一种线性结构,它是一个含有n>=0和结点的有限序列,同一个线性表中的数据元素类型相同并且满足“一对一”的逻辑关系。
“一对一”的逻辑关系,指的是除了表头和表尾的结点外,其余每个结点有且仅有一个前驱和一个后继结点。
栈和队列是两种操作受限的线性表。
1. 栈和队列的相同点
(1)都是线性结构。
(2)插入操作都是限定在表尾进行。(栈的栈顶,队列的队尾)
(3)都可以通过顺序存储结构和链式存储结构实现。
(4)插入和删除的时间复杂度都是O(1),在空间复杂度上两者也一样。
(5)多链栈和多链队列的管理模式可以相同。
2. 栈和队列的不同点
(1)删除元素的位置不同,栈的操作在表尾进行,队列的删除操作在表头进行。
(2)应用场景:常见的栈的应用场景有括号问题的求解,表达式的转换和求值,函数调用和递归实现,深度优先搜索遍历等;常见的队列的应用场景包括计算机系统中各种资源的管理,消息缓冲器的管理和广度优先遍历、还可用于实现打印机打印的冲突以及多个客户访问服务器的文件时,满足先来先服务的原则等。
(3)顺序栈能够实现多栈空间共享,而顺序队列不能。
相关文章:

C/C++每日一练(20230219)
目录 1. 用队列实现栈 2. 判断是否能组成三角形 3. 只出现一次的数字 II 附录 栈(Stack)和队列(Queue)的异同 1. 栈和队列的相同点 2. 栈和队列的不同点 1. 用队列实现栈 请你仅使用两个队列实现一个后入先出(…...

【NestJS】模块
脚手架中,可以执行 nest g mo XXX 创建模块。通过脚手架命令创建的模块,会自动被导入至根模块注册。 注意:项目中的模块都需要导入到根模块中注册一下才能被使用。 共享模块 nest g res boy、nest g res girl 如果希望在 girl 模块中使用 …...

隐私计算头条周刊(2.13-2.19)
开放隐私计算收录于合集#企业动态44个#周刊合辑44个#政策聚焦37个#隐私计算91个#行业研究36个开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播…...
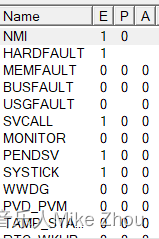
【STM32笔记】低功耗模式配置及避坑汇总
【STM32笔记】低功耗模式配置及配置汇总 文章总结:(后续更新以相关文章为准) 【STM32笔记】__WFI();进入不了休眠的可能原因 【STM32笔记】HAL库低功耗模式配置(ADC唤醒无法使用、低功耗模式无法烧录解决方案&#x…...
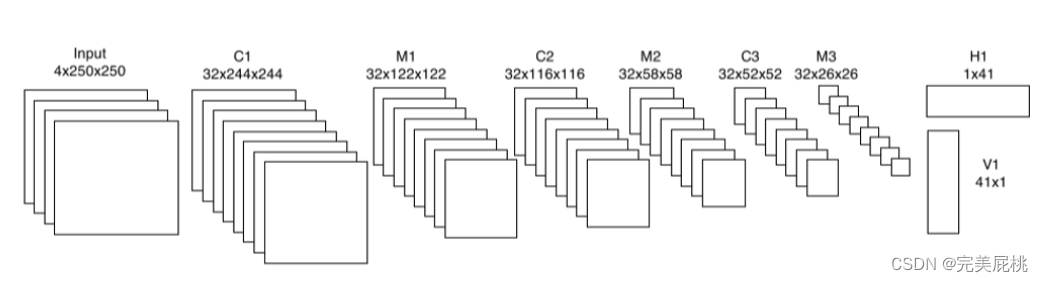
DFN: Dynamic Filter Networks-动态卷积网络
一、论文信息 论文名称:Dynamic Filter Networks 作者团队:NIPS2016 二、动机与创新 卷积层是通过将上一层的特征映射与一组过滤器进行卷积计算输出特征映射,滤波器是卷积层的唯一参数,通常用反向传播算法在训练中学习ÿ…...
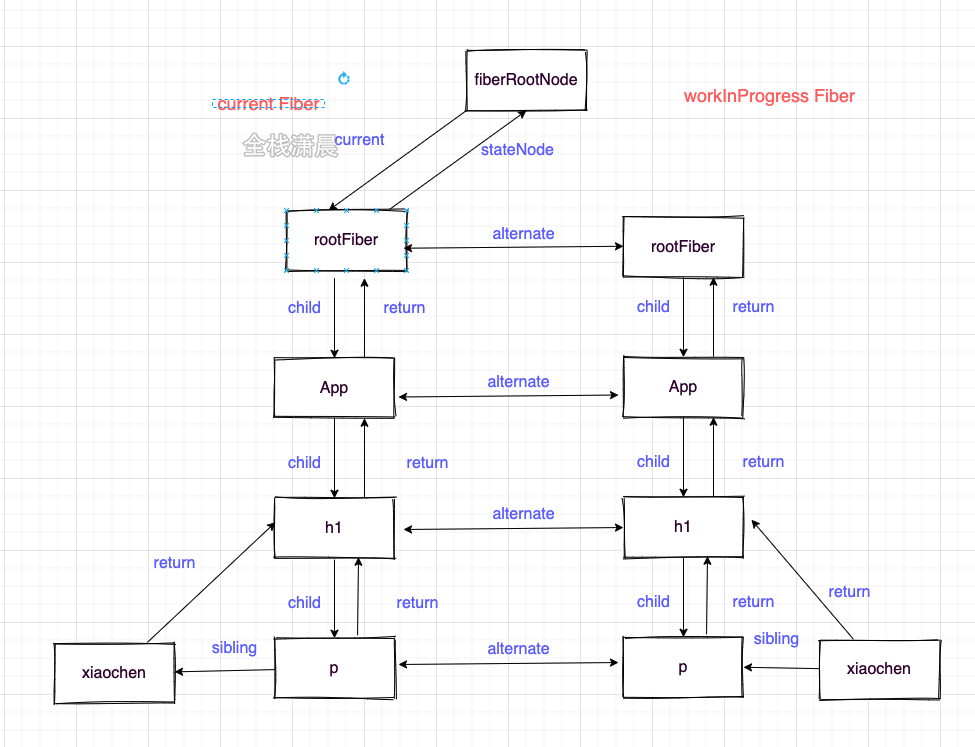
面试官:你是怎样理解Fiber的
hello,这里是潇晨,今天我们来聊一聊Fiber。不知道大家面试的时候有没有遇到过和react Fiber相关的问题呢,这一类问题比较开放,但也是考察对react源码理解深度的问题,如果面试高级前端岗,恰巧你平时用的是re…...

【C++的OpenCV】第一课-opencv的介绍和安装(Linux环境下)
第一课-目录一、基本介绍1.1 官网1.2 git源码1.3 介绍二、OpenCV的相关部署工作2.1 Linux平台下部署OpenCV一、基本介绍 1.1 官网 opencv官网 注意:官网为英文版本,可以使用浏览器自带的翻译插件进行翻译,真心不推荐大家去看别人翻译的&am…...
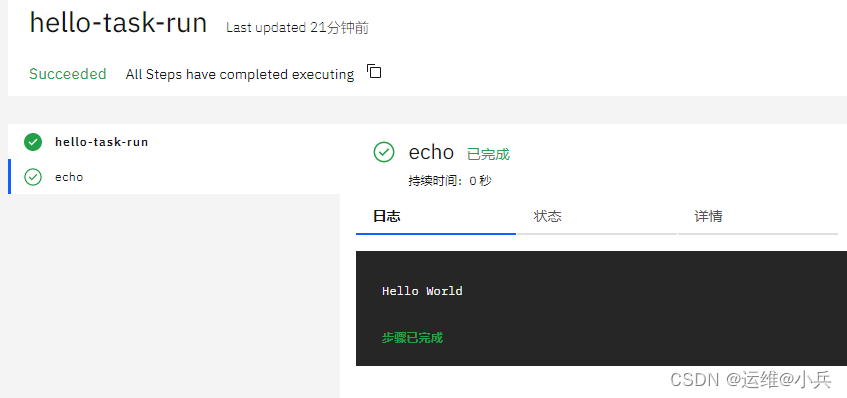
k8s安装tekton,编写task
文章目录一、官方安装二、国内资源安装安装tekton安装dashboard安装CLI三、demo编写task.yaml编写taskRun.yaml使用tkn命令查看参考文章一、官方安装 地址:https://tekton.dev/docs/installation/pipelines/#installing-tekton-pipelines-on-kubernetes 注意&#…...

K_A12_014 基于STM32等单片机驱动S12SD紫外线传感器模块 串口与OLED0.96双显示
K_A12_014 基于STM32等单片机驱动S12SD紫外线传感器模块 串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:数据对比:四、部分代码说明1、接线引脚定义1.1、STC89C52RCS12SD紫外线传感器模块1.2、STM32F103…...
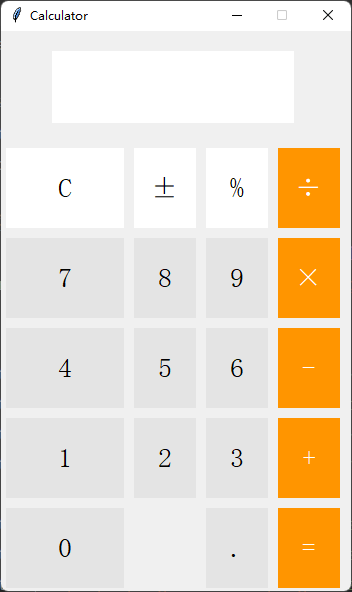
还真不错,今天 Chatgpt 教会我如何开发一款小工具开发(Python 代码实现)
上次使用 Chatgpt 写爬虫,虽然写出来的代码很多需要修改后才能运行,但Chatgpt提供的思路和框架都是没问题。 这次让 Chatgpt 写一写GUI程序,也就是你常看到的桌面图形程序。 由于第一次测试,就来个简单点的,用Python…...
Boom 3D最新版本下载电脑音频增强应用工具
为了更好地感受音乐的魅力,Boom 3D 可以让你对音效进行个性化增强,并集成 3D 环绕立体声效果,可以让你在使用任何耳机时,都拥有纯正、优质的音乐体验。Boom 3D是一款充满神奇魅力的3D环绕音效升级版,BOOM 3D是一个全新…...

redis-如何保证数据库和缓存双写一致性?
前言 数据库和缓存(比如:redis)双写数据一致性问题,是一个跟开发语言无关的公共问题。尤其在高并发的场景下,这个问题变得更加严重。 我很负责的告诉大家,该问题无论在面试,还是工作中遇到的概率…...
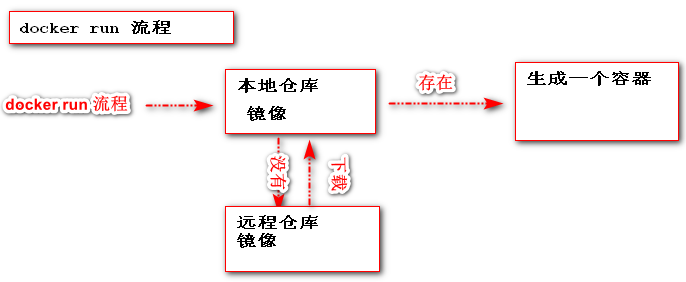
系列二、核心概念运行流程
一、镜像&容器&仓库 1.1、镜像 定义:一个镜像代表着一个软件,例如:mysql镜像、redis镜像、nginx镜像。 特点:只读 1.2、容器 定义:基于某个镜像运行一次就会生成一个程序实例,一个程序实例称之为一…...
恢复 iPhone 和 iPad 数据的 10 种简单工具
它发生了.. 有时您需要从您的手机或平板设备恢复重要数据。 许多人已经开始将重要文件存储在手机上,因为他们几乎可以在任何情况下随时随地轻松访问数据。 从技术上讲,您会在几分之一秒内丢失所有存储的信息、照片、视频、音乐、文档等。因此ÿ…...
经理与员工工资关系-课后程序(JAVA基础案例教程-黑马程序员编著-第四章-课后作业)
【案例4-6】经理与员工工资案例(利用多态实现) 欢迎点赞关注收藏 【案例介绍】 案例描述 某公司的人员分为员工和经理两种,但经理也属于员工中的一种,公司的人员都有自己的姓名和地址,员工和经理都有自己的工号、工…...
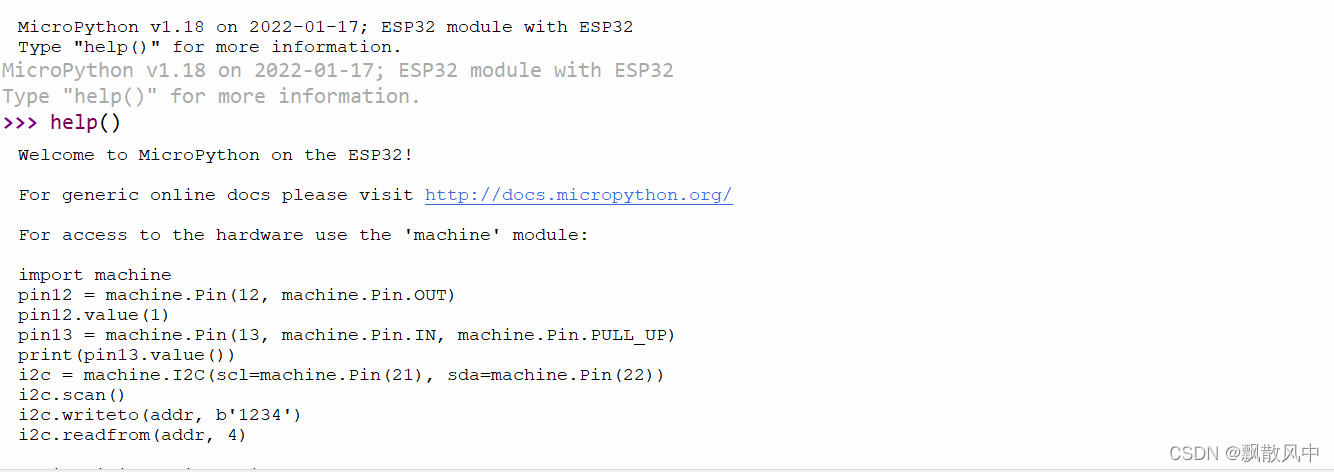
Micropython ESP32配置与烧录版本
下载ESP32的Micropython固件 官方连接https://www.micropython.org/download/esp32/ 看了下描述,上面的是IDF4.x系列编译,下面是IDF3.x系列编译,我们默认选新的 下载安装CP2102驱动 CP210x USB to UART Bridge VCP Drivers - Silicon Labs…...
)
java面试题-并发关键字(Synchronized,volatile,final)
Synchronized1.Synchronized可以作用在哪里?Synchronized可以作用在方法、代码块、静态方法和类上。方法public synchronized void method(){//同步代码块 }代码块Object lock new Object(); synchronized(lock){//同步代码块 }静态方法public static synchronized void stat…...
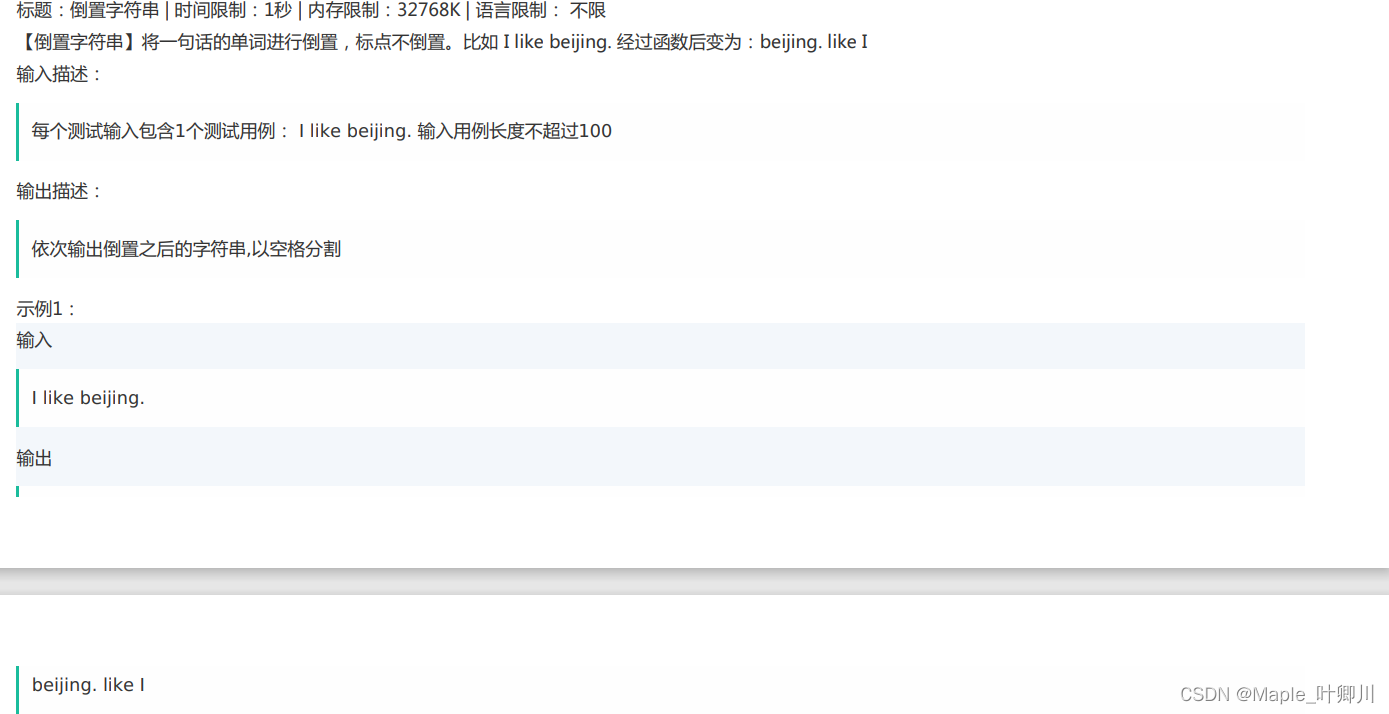
【笔试强训】Day_02
目录 一、选择题 1、 2、 3、 4、 5、 6、 7、 8、 9、 10、 二、编程题 1、排序子序列 2、倒置字符串 一、选择题 1、 使用printf函数打印一个double类型的数据,要求:输出为10进制,输出左对齐30个字符,4位精度。…...

DepGraph:适用任何结构的剪枝
文章目录摘要1、简介2、相关工作3、方法3.1、神经网络中的依赖关系3.2、依赖关系图3.3、使用依赖图剪枝4、实验4.1、设置。4.2、CIFAR的结果4.3、消融实验4.4、适用任何结构剪枝5、结论摘要 论文链接:https://arxiv.org/abs/2301.12900 源码:https://gi…...
【结构体版】通讯录
👦个人主页:Weraphael ✍🏻作者简介:目前是C语言学习者 ✈️专栏:项目 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞&#x…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
