【数据结构】时间复杂度和空间复杂度

🌇个人主页:平凡的小苏
📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情
🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html
小苏希望大家能从这篇文章中收获到许多,如果大家觉得这篇文章对你有帮助,请给小苏点赞+收藏+评论
目录
1.算法效率
1.1 如何衡量一个算法的好坏
2. 时间复杂度
2.1时间复杂度的概念
2.2 大O的渐进表示法
3.空间复杂度
4.由数据范围反推算法复杂度以及算法内容
1.算法效率
1.1 如何衡量一个算法的好坏
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
2. 时间复杂度
2.1时间复杂度的概念
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{for (int j = 0; j < N ; ++ j){++count;}
}for (int k = 0; k < 2 * N ; ++ k)
{++count;
}
int M = 10;
while (M--)
{++count;
}
printf("%d\n", count);
}Func1 执行的基本操作次数 :
F(N) = N^2+2*N+10
- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
- N = 10 F(N) = 100
- N = 100 F(N) = 10000
- N = 1000 F(N) = 1000000
3.空间复杂度
4.由数据范围反推算法复杂度以及算法内容

好了!小编的分享到这里就结束了,有什么不足的地方请大佬多多指教!!!
相关文章:

【数据结构】时间复杂度和空间复杂度
🌇个人主页:平凡的小苏 📚学习格言:别人可以拷贝我的模式,但不能拷贝我不断往前的激情 🛸C语言专栏:https://blog.csdn.net/vhhhbb/category_12174730.html 小苏希望大家能从这篇文章中收获到许…...

从发现SQL注入到ssh连接
前言: 某天,同事扔了一个教育站点过来,里面的url看起来像有SQL注入。正好最近手痒痒,就直接开始。 一、发现时间盲注和源码 后面发现他发的url是不存在SQL注入的,但是我在其他地方发现了SQL盲注。然后改站点本身也可…...
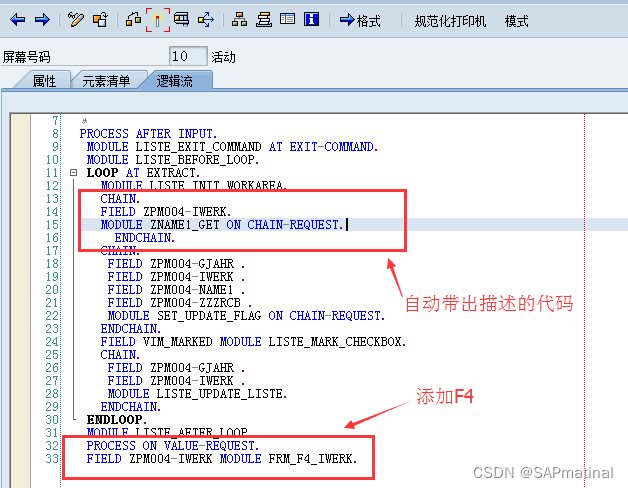
SAP ABAP
方法一: REPORT ZDCH_09_TEST2. ************************************************************************ * DATEN DEFINITION * *********************************************************************…...

C/C++每日一练(20230219)
目录 1. 用队列实现栈 2. 判断是否能组成三角形 3. 只出现一次的数字 II 附录 栈(Stack)和队列(Queue)的异同 1. 栈和队列的相同点 2. 栈和队列的不同点 1. 用队列实现栈 请你仅使用两个队列实现一个后入先出(…...

【NestJS】模块
脚手架中,可以执行 nest g mo XXX 创建模块。通过脚手架命令创建的模块,会自动被导入至根模块注册。 注意:项目中的模块都需要导入到根模块中注册一下才能被使用。 共享模块 nest g res boy、nest g res girl 如果希望在 girl 模块中使用 …...

隐私计算头条周刊(2.13-2.19)
开放隐私计算收录于合集#企业动态44个#周刊合辑44个#政策聚焦37个#隐私计算91个#行业研究36个开放隐私计算开放隐私计算OpenMPC是国内第一个且影响力最大的隐私计算开放社区。社区秉承开放共享的精神,专注于隐私计算行业的研究与布道。社区致力于隐私计算技术的传播…...
【STM32笔记】低功耗模式配置及避坑汇总
【STM32笔记】低功耗模式配置及配置汇总 文章总结:(后续更新以相关文章为准) 【STM32笔记】__WFI();进入不了休眠的可能原因 【STM32笔记】HAL库低功耗模式配置(ADC唤醒无法使用、低功耗模式无法烧录解决方案&#x…...
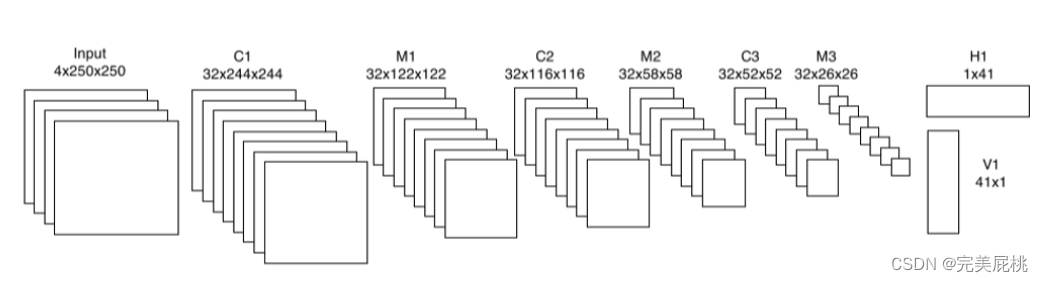
DFN: Dynamic Filter Networks-动态卷积网络
一、论文信息 论文名称:Dynamic Filter Networks 作者团队:NIPS2016 二、动机与创新 卷积层是通过将上一层的特征映射与一组过滤器进行卷积计算输出特征映射,滤波器是卷积层的唯一参数,通常用反向传播算法在训练中学习ÿ…...
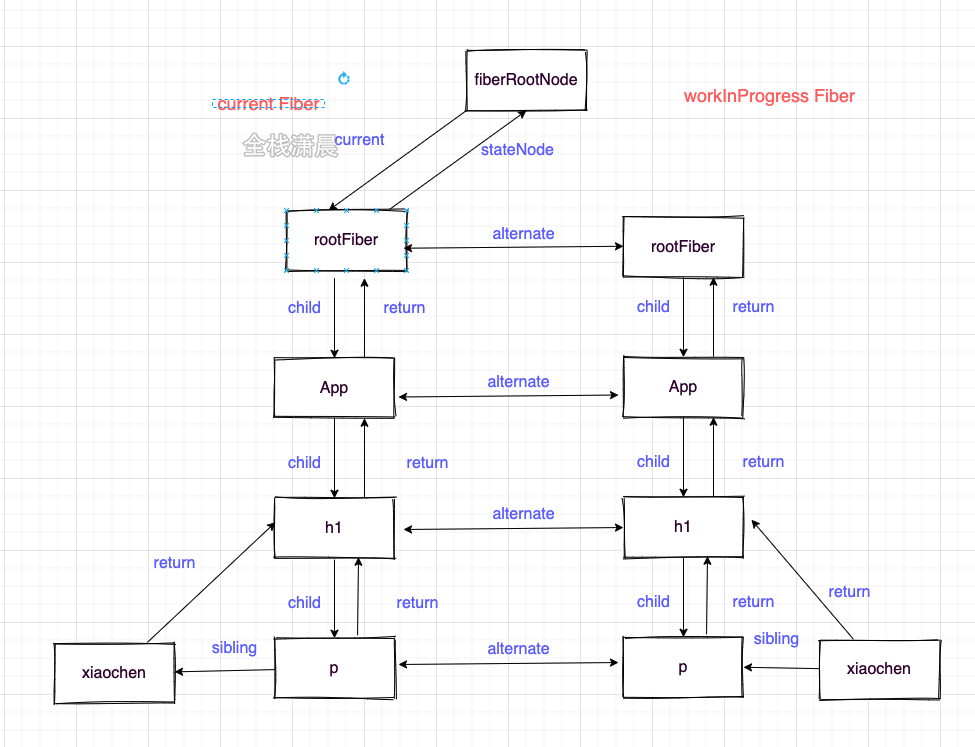
面试官:你是怎样理解Fiber的
hello,这里是潇晨,今天我们来聊一聊Fiber。不知道大家面试的时候有没有遇到过和react Fiber相关的问题呢,这一类问题比较开放,但也是考察对react源码理解深度的问题,如果面试高级前端岗,恰巧你平时用的是re…...

【C++的OpenCV】第一课-opencv的介绍和安装(Linux环境下)
第一课-目录一、基本介绍1.1 官网1.2 git源码1.3 介绍二、OpenCV的相关部署工作2.1 Linux平台下部署OpenCV一、基本介绍 1.1 官网 opencv官网 注意:官网为英文版本,可以使用浏览器自带的翻译插件进行翻译,真心不推荐大家去看别人翻译的&am…...
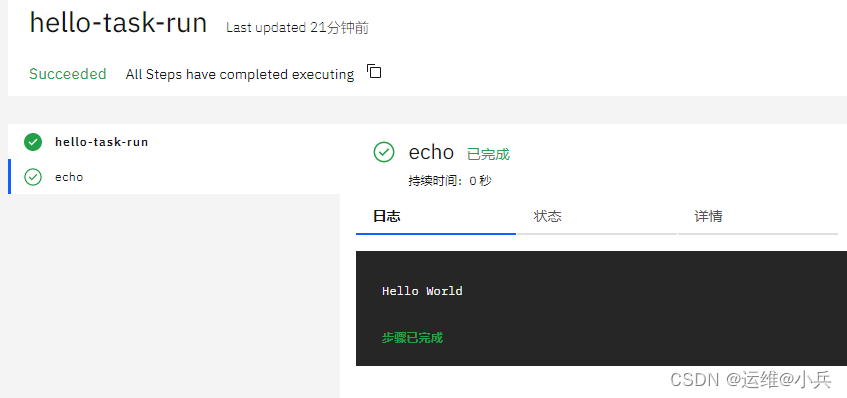
k8s安装tekton,编写task
文章目录一、官方安装二、国内资源安装安装tekton安装dashboard安装CLI三、demo编写task.yaml编写taskRun.yaml使用tkn命令查看参考文章一、官方安装 地址:https://tekton.dev/docs/installation/pipelines/#installing-tekton-pipelines-on-kubernetes 注意&#…...

K_A12_014 基于STM32等单片机驱动S12SD紫外线传感器模块 串口与OLED0.96双显示
K_A12_014 基于STM32等单片机驱动S12SD紫外线传感器模块 串口与OLED0.96双显示一、资源说明二、基本参数参数引脚说明三、驱动说明IIC地址/采集通道选择/时序对应程序:数据对比:四、部分代码说明1、接线引脚定义1.1、STC89C52RCS12SD紫外线传感器模块1.2、STM32F103…...
还真不错,今天 Chatgpt 教会我如何开发一款小工具开发(Python 代码实现)
上次使用 Chatgpt 写爬虫,虽然写出来的代码很多需要修改后才能运行,但Chatgpt提供的思路和框架都是没问题。 这次让 Chatgpt 写一写GUI程序,也就是你常看到的桌面图形程序。 由于第一次测试,就来个简单点的,用Python…...
Boom 3D最新版本下载电脑音频增强应用工具
为了更好地感受音乐的魅力,Boom 3D 可以让你对音效进行个性化增强,并集成 3D 环绕立体声效果,可以让你在使用任何耳机时,都拥有纯正、优质的音乐体验。Boom 3D是一款充满神奇魅力的3D环绕音效升级版,BOOM 3D是一个全新…...

redis-如何保证数据库和缓存双写一致性?
前言 数据库和缓存(比如:redis)双写数据一致性问题,是一个跟开发语言无关的公共问题。尤其在高并发的场景下,这个问题变得更加严重。 我很负责的告诉大家,该问题无论在面试,还是工作中遇到的概率…...
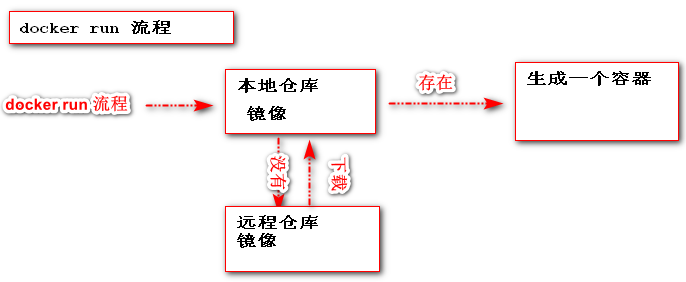
系列二、核心概念运行流程
一、镜像&容器&仓库 1.1、镜像 定义:一个镜像代表着一个软件,例如:mysql镜像、redis镜像、nginx镜像。 特点:只读 1.2、容器 定义:基于某个镜像运行一次就会生成一个程序实例,一个程序实例称之为一…...
恢复 iPhone 和 iPad 数据的 10 种简单工具
它发生了.. 有时您需要从您的手机或平板设备恢复重要数据。 许多人已经开始将重要文件存储在手机上,因为他们几乎可以在任何情况下随时随地轻松访问数据。 从技术上讲,您会在几分之一秒内丢失所有存储的信息、照片、视频、音乐、文档等。因此ÿ…...
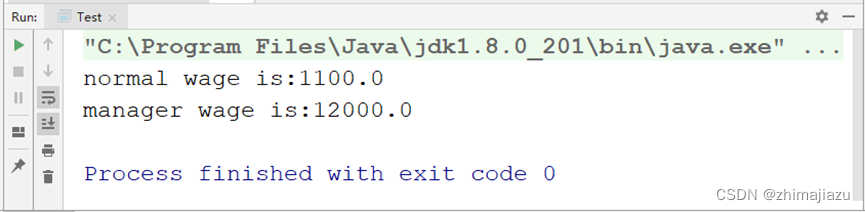
经理与员工工资关系-课后程序(JAVA基础案例教程-黑马程序员编著-第四章-课后作业)
【案例4-6】经理与员工工资案例(利用多态实现) 欢迎点赞关注收藏 【案例介绍】 案例描述 某公司的人员分为员工和经理两种,但经理也属于员工中的一种,公司的人员都有自己的姓名和地址,员工和经理都有自己的工号、工…...
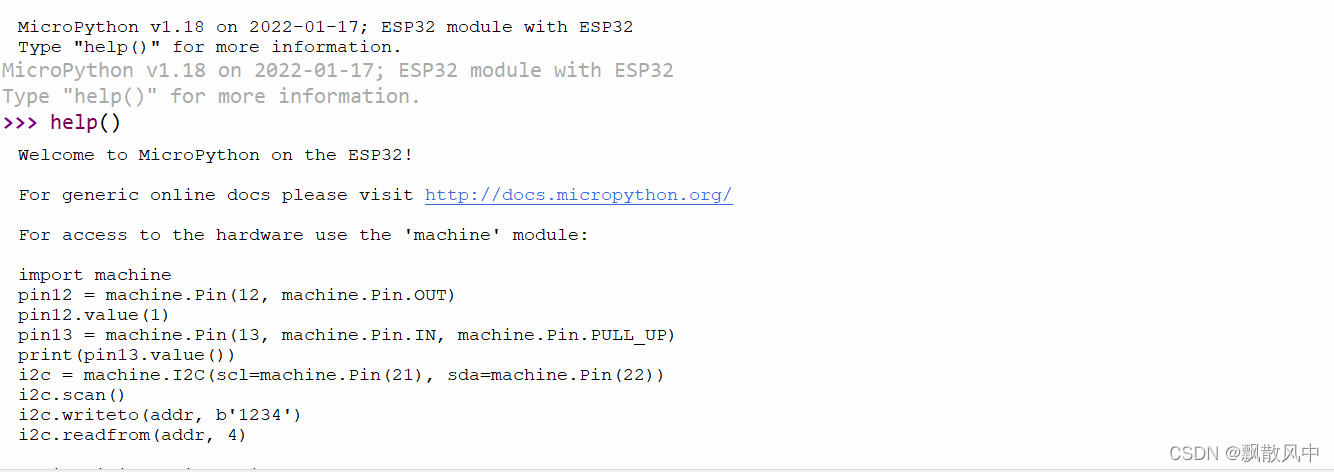
Micropython ESP32配置与烧录版本
下载ESP32的Micropython固件 官方连接https://www.micropython.org/download/esp32/ 看了下描述,上面的是IDF4.x系列编译,下面是IDF3.x系列编译,我们默认选新的 下载安装CP2102驱动 CP210x USB to UART Bridge VCP Drivers - Silicon Labs…...
)
java面试题-并发关键字(Synchronized,volatile,final)
Synchronized1.Synchronized可以作用在哪里?Synchronized可以作用在方法、代码块、静态方法和类上。方法public synchronized void method(){//同步代码块 }代码块Object lock new Object(); synchronized(lock){//同步代码块 }静态方法public static synchronized void stat…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
