当前位置： 首页 > news >正文

2023-8-23 滑动窗口

news 文章来源：https://blog.csdn.net/weixin_63522344/article/details/132439812 2024/9/22 7:40:25

题目链接：滑动窗口
在这里插入图片描述

#include <iostream>using namespace std;const int N = 1000010;int n, k;
int a[N], q[N];int main()
{scanf("%d%d", &n, &k);for(int i = 0; i < n; i++) scanf("%d", &a[i]);int hh = 0, tt = -1;for(int i = 0; i < n; i ++){// 队头出队条件if(hh <= tt && i - k + 1 > q[hh]) hh++;// 队尾出队条件while(hh <= tt && a[q[tt]] >= a[i]) tt--;q[++tt] = i;if(i >= k - 1) printf("%d ", a[q[hh]]);}puts("");hh = 0, tt = -1;for(int i = 0; i < n; i ++){// 队头出队条件if(hh <= tt && i - k + 1 > q[hh]) hh++;// 队尾出队条件while(hh <= tt && a[q[tt]] <= a[i]) tt--;q[++tt] = i;if(i >= k - 1) printf("%d ", a[q[hh]]);}return 0;
}

相关文章：

2023-8-23 滑动窗口

题目链接&#xff1a;滑动窗口 #include <iostream>using namespace std;const int N 1000010;int n, k; int a[N], q[N];int main() {scanf("%d%d", &n, &k);for(int i 0; i < n; i) scanf("%d", &a[i]);int hh 0, tt -1;for(…...

编程日记 2023/8/23 5:31:35

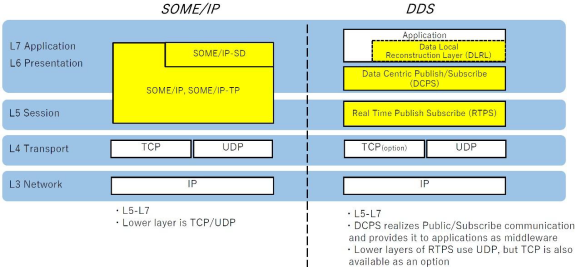
SOA通信中间件常用的通信协议

摘要&#xff1a; SOA&#xff08;面向服务的架构&#xff09;的软件设计原则之一是模块化。 前言 SOA&#xff08;面向服务的架构&#xff09;的软件设计原则之一是模块化。模块化可以提高软件系统的可维护性和代码重用性&#xff0c;并且能够隔离故障。举例来说&#xff0c;…...

编程日记 2023/8/23 5:30:34

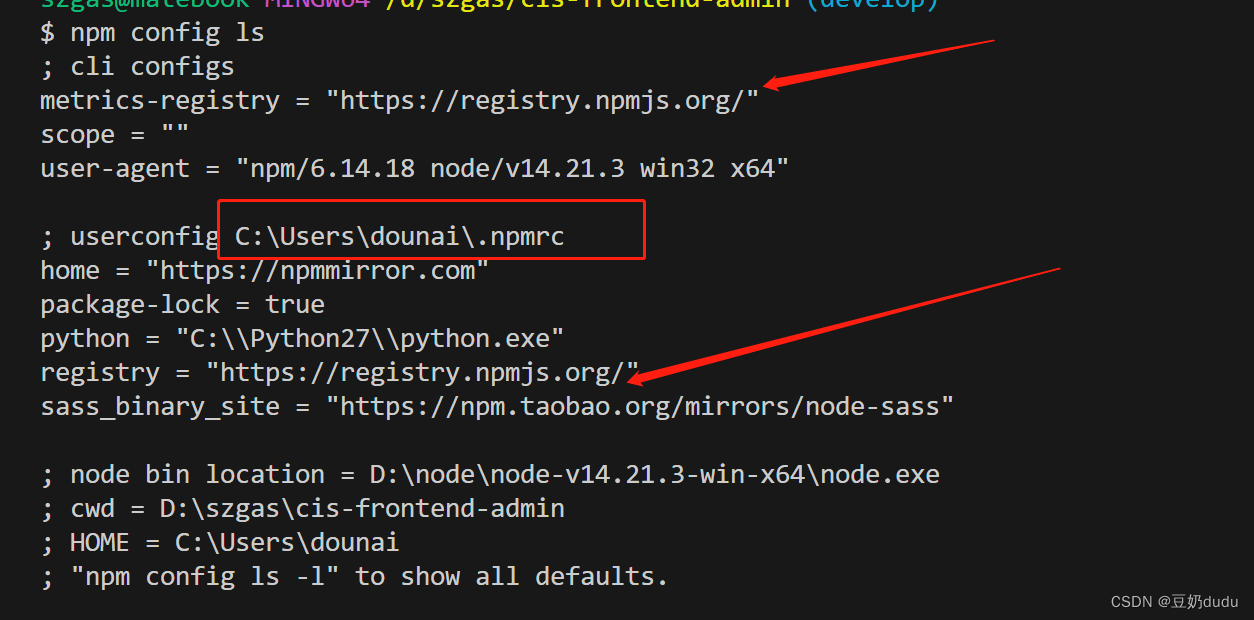
解决npm安装依赖失败，node和node-sass版本不匹配的问题

npm安装依赖报错&#xff1a; npm ERR! cb() never called! npm ERR! This is an error with npm itself. 一. 问题描述 用npm安装依赖报错&#xff1a; npm ERR! cb() never called! npm ERR! This is an error with npm itself. Please report this error at: npm ERR! …...

编程日记 2023/8/23 5:29:33

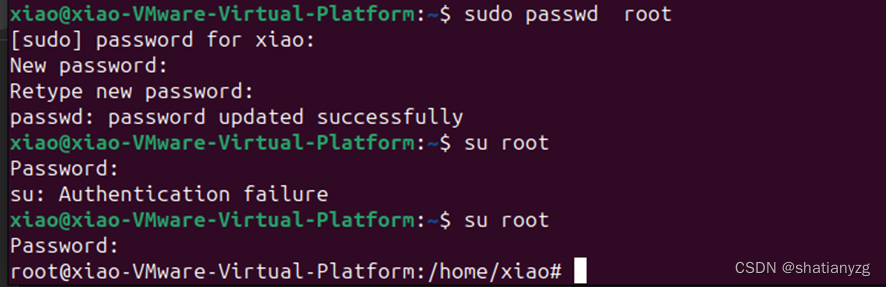
2023 网络建设与运维 X86架构计算机操作系统安装与管理题解

任务描述： 随着信息技术的快速发展，集团计划2023年把部分业务由原有的X86架构服务器上迁移到ARM架构服务器上，同时根据目前的部分业务需求进行了部分调整和优化。 一、X86架构计算机操作系统安装与管理 1.PC1系统为ubuntu-desktop-amd64系统（已安装，语言为英文），登录用户…...

编程日记 2023/8/23 5:28:31

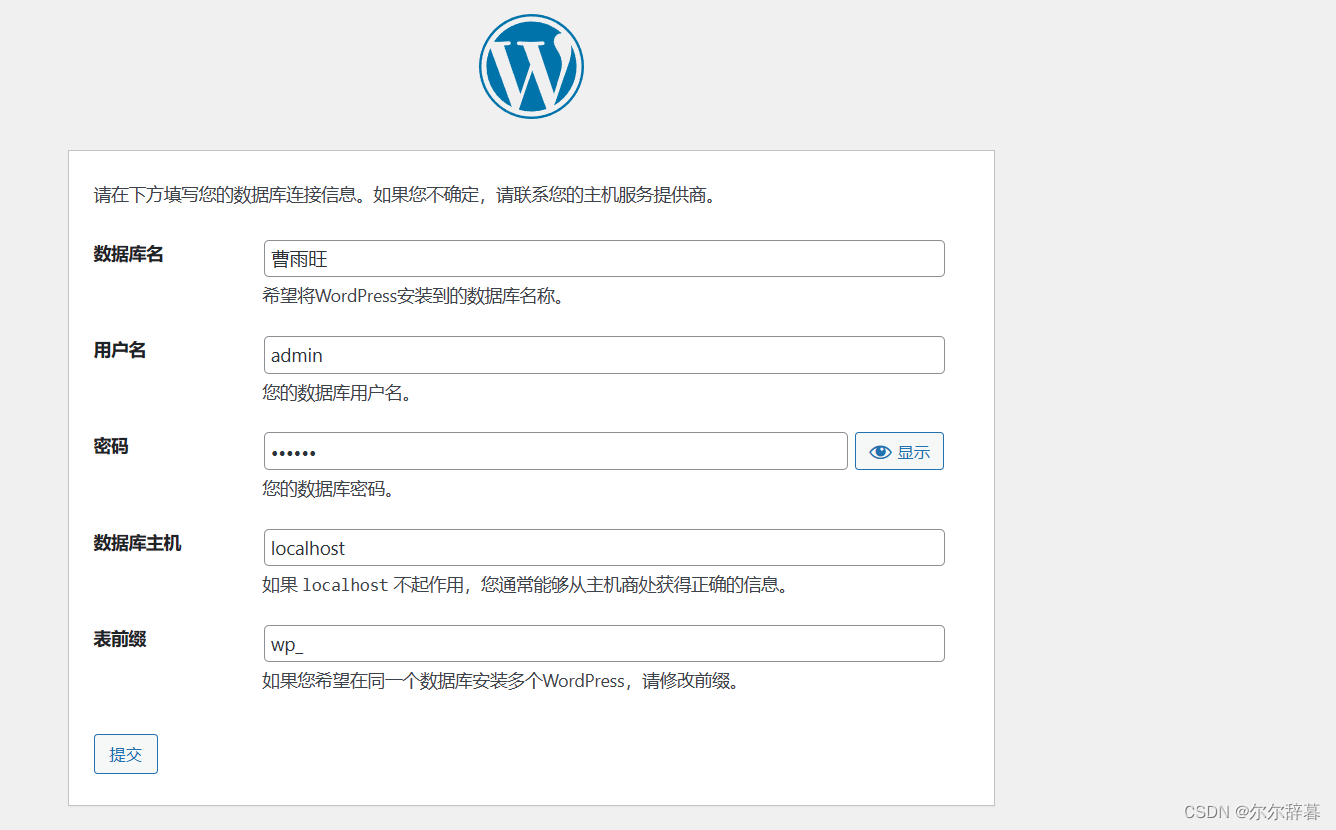
LAMP 架构及Discuz论坛与Wordpress博客搭建

目录 1 LAMP 配置与应用 1.1动态资源与语言 1.2 LAMP 架构的组成 1.2.1 主要功能 2 编译安装Apache http 服务 2.1 环境准备 2.1.1 关闭防火墙及selinux服务 2.1.2 安装依赖环境 2.2 安装软件包 2.2.1 解压软件包 2.2.2 移动apr包 apr-util包到安装目录中&#xff0c;并…...

编程日记 2023/8/23 5:27:30

考研C语言进阶题库——更新51-60题

目录 51.银行系中有很多恒星&#xff0c;H 君晚上无聊&#xff0c;便爬上房顶数星星&#xff0c;H 君将整个银河系看做一个平面&#xff0c;左上角为原点&#xff08;坐标为&#xff08;1, 1&#xff09;&#xff09;。现在有 n 颗星星&#xff0c;他给每颗星星都标上坐标&…...

编程日记 2023/8/23 5:26:27

智能算法挑战赛决赛题目——初中组

题目 1. 判断是否存在重复的子序列 从 m 个字符中选取字符&#xff0c;生成 n 个符号的序列&#xff0c;使得其中没有 2 个相邻的子序列相同。如从 1&#xff0c;2&#xff0c;3&#xff0c;生成长度为 5 的序列&#xff0c;序列“12321”是合格的&#xff0c;而“12323”和“…...

编程日记 2023/8/23 5:25:26

一分钟学算法-递归-斐波那契数列递归解法及优化

一分钟学一个算法题目。 今天我们要学习的是用递归算法求解斐波那契数列。 首先我们要知道什么是斐波那契数列。 斐波那契数列&#xff0c;又称黄金分割数列&#xff0c;是一个经典的数学数列&#xff0c;其特点是第一项&#xff0c;第二项为1&#xff0c;后面每个数字都是前…...

编程日记 2023/8/23 5:24:25

选择Rust，并在Ubuntu上使用Rust

在过去的 8 年里&#xff0c;Rust 一直是开发人员最喜欢的语言&#xff0c;并且越来越被各种规模的软件公司采用。然而&#xff0c;它的许多高级规则和抽象创造了一个陡峭的初始学习曲线&#xff0c;这可能会给人留下 Rust 是少数人的保留的印象&#xff0c;但这与事实相去甚远…...

编程日记 2023/8/23 5:23:24

SVM详解

公式太多了&#xff0c;就用图片用笔记呈现&#xff0c;SVM虽然算法本质一目了然&#xff0c;但其中用到的数学推导还是挺多的&#xff0c;其中拉格朗日约束关于α>0这块证明我看了很长时间&#xff0c;到底是因为悟性不够。对偶问题也是&#xff0c;用了一个简单的例子才明…...

编程日记 2023/8/23 5:22:23

mysql全文检索使用

数据库数据量10万左右&#xff0c;使用like %test%要耗费30秒左右&#xff0c;放弃该办法 使用mysql的全文检索 第一步:建立索引 首先修改一下设置: my.ini中ngram_token_size 1 可以通过 show variables like %token%;来查看 接下来建立索引:alter table 表名 add f…...

编程日记 2023/8/23 5:21:21

opencv 进阶17-使用K最近邻和比率检验过滤匹配（图像匹配）

K最近邻&#xff08;K-Nearest Neighbors&#xff0c;简称KNN&#xff09;和比率检验&#xff08;Ratio Test&#xff09;是在计算机视觉中用于特征匹配的常见技术。它们通常与特征描述子&#xff08;例如SIFT、SURF、ORB等&#xff09;一起使用&#xff0c;以在图像中找到相似…...

编程日记 2023/8/23 5:20:20

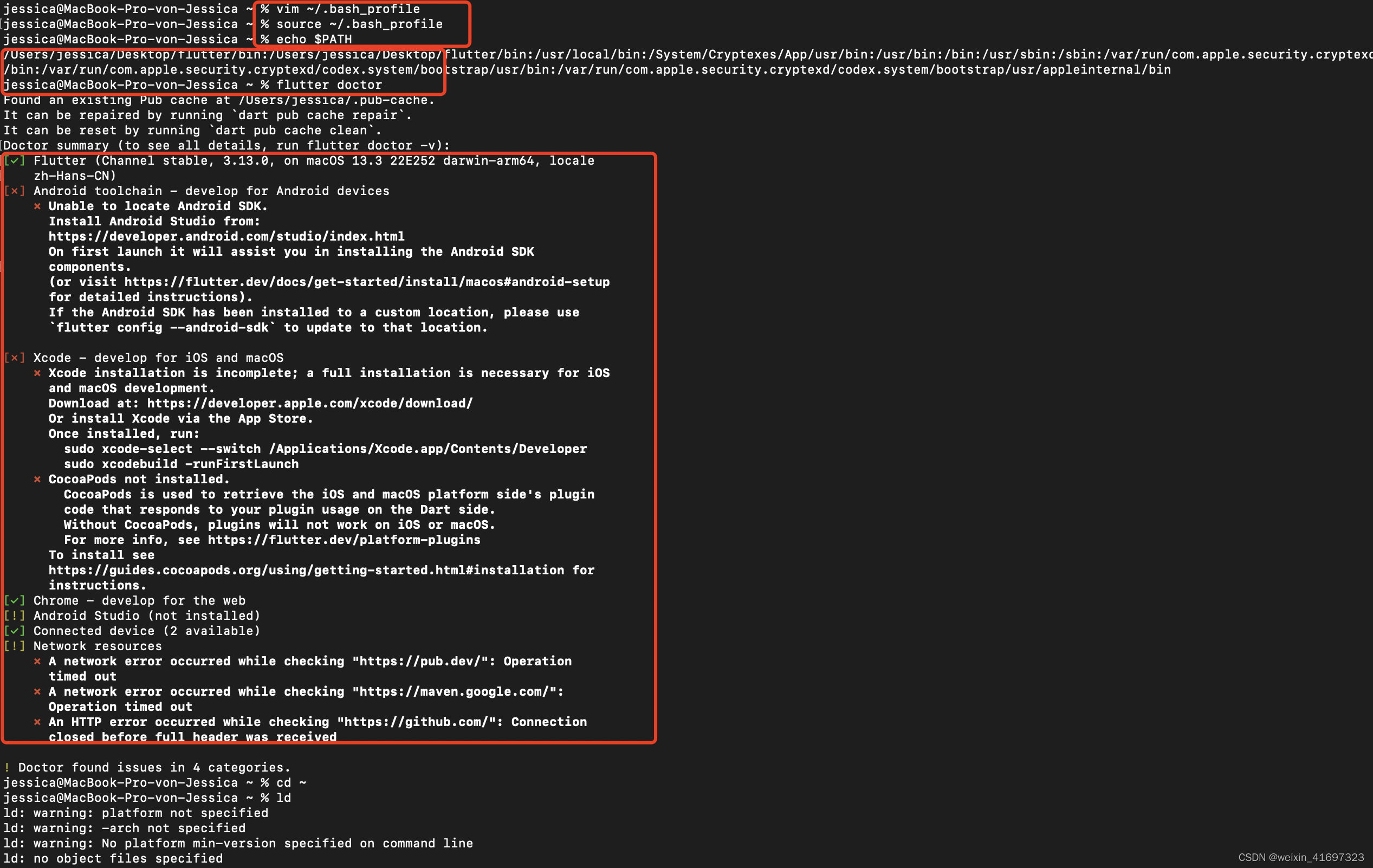
Mac Flutter web环境搭建

获取 Flutter SDK 下载以下安装包来获取最新的 stable Flutter SDK将文件解压到目标路径, 比如: cd ~/development $ unzip ~/Downloads/flutter_macos_3.13.0-stable.zip 配置 flutter 的 PATH 环境变量&#xff1a; export PATH"$PATH:pwd/flutter/bin" // 这个命…...

编程日记 2023/8/23 5:19:19

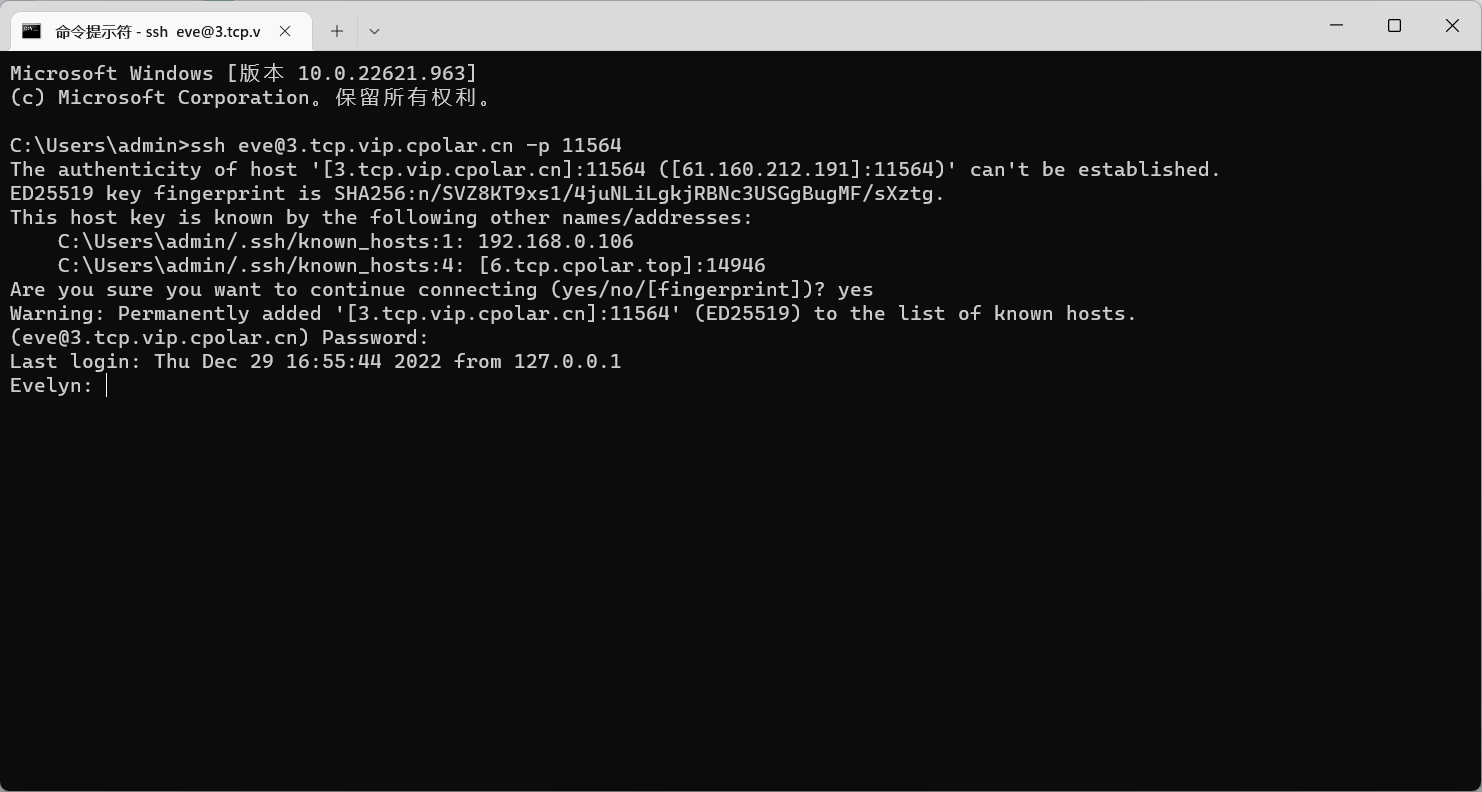
在外SSH远程连接macOS服务器

文章目录 前言1. macOS打开远程登录2. 局域网内测试ssh远程3. 公网ssh远程连接macOS3.1 macOS安装配置cpolar3.2 获取ssh隧道公网地址3.3 测试公网ssh远程连接macOS 4. 配置公网固定TCP地址4.1 保留一个固定TCP端口地址4.2 配置固定TCP端口地址 5. 使用固定TCP端口地址ssh远程 …...

编程日记 2023/8/23 5:18:17

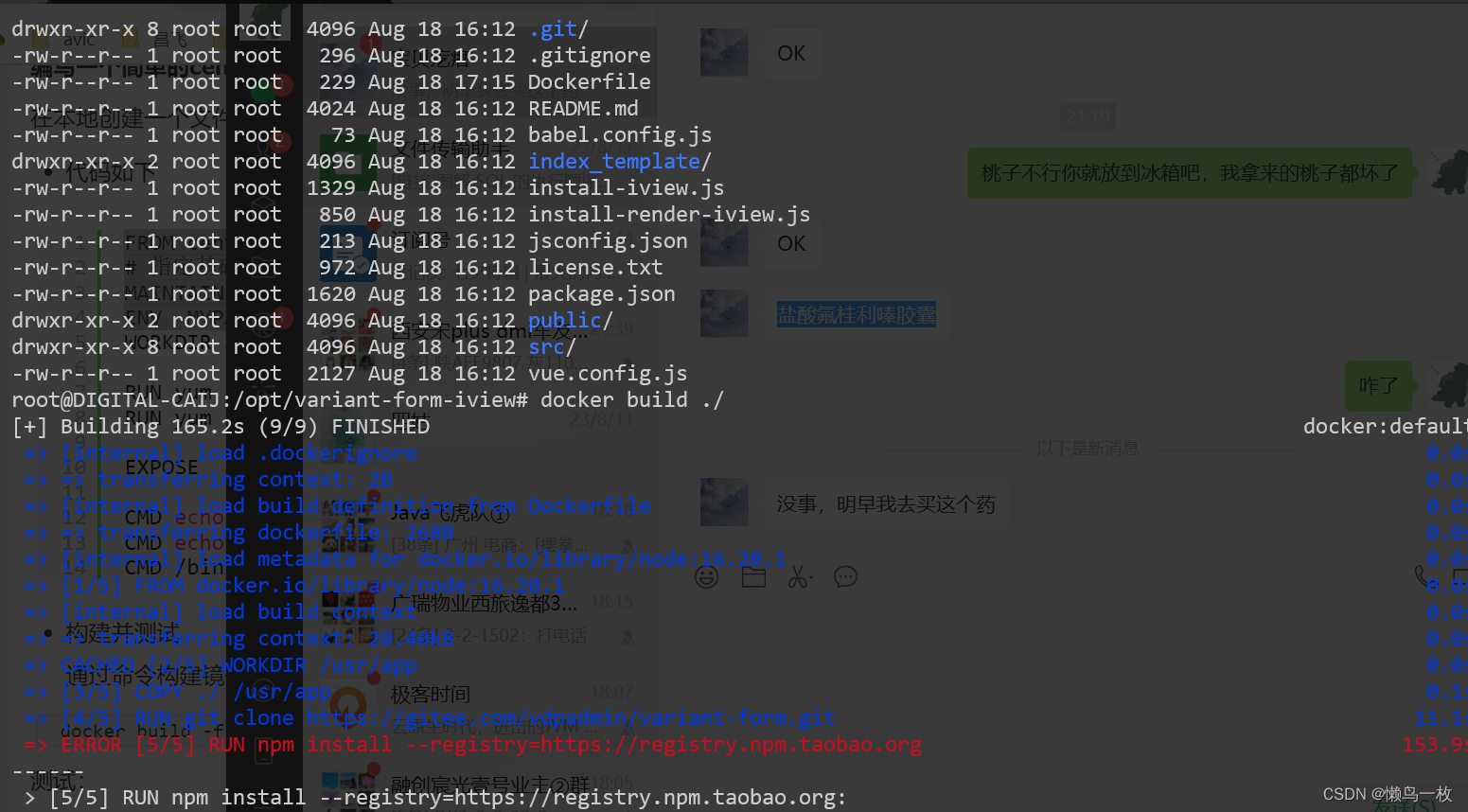
Dockerfile文件详细

Dockerfile 是一个文本文件&#xff0c;里面包含组装新镜像时用到的基础镜像和各种指令&#xff0c;使用dockerfile 文件来定义镜像&#xff0c;然后运行镜像&#xff0c;启动容器。 dockerfile文件的组成部分 一个dockerfile文件包含以下部分&#xff1a; 基础镜像信息&…...

编程日记 2023/8/23 5:17:16

C语言学习系列--＞看淡指针（3）

文章目录 一、字符指针变量二、数组指针变量2.1 概述2.2 数组指针初始化 三、二维数组传参本质四、函数指针五、typedef关键字六、函数指针数组 一、字符指针变量 在指针的类型中我们知道有⼀种指针类型为字符指针 char* 一般使用&#xff1a; #include<stdio.h>int main…...

编程日记 2023/8/23 5:16:15

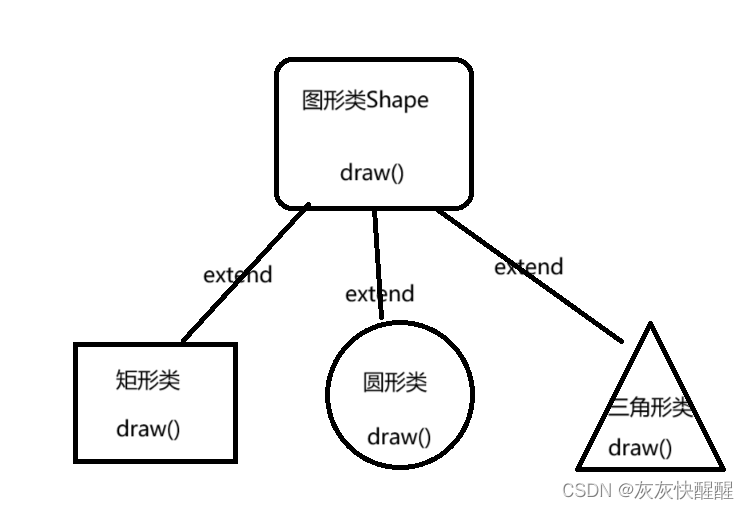
Java抽象类详解

抽象类 抽象类的概念 在面向对象的概念中&#xff0c;所有的对象都是通过类来描绘的&#xff0c;但是反过来&#xff0c;并不是所有的类都是来描绘对象的&#xff0c;如果一个类中没有包含足够的信息来描绘一个具体的对象&#xff0c;这样的类就是抽象类。比如&#xff1a; 说…...

编程日记 2023/8/23 5:15:14

06-微信小程序-注册程序-场景值

06-微信小程序-注册程序 文章目录 注册小程序参数 Object object案例代码 场景值场景值作用场景值列表案例代码 注册小程序 每个小程序都需要在 app.js 中调用 App 方法注册小程序实例&#xff0c;绑定生命周期回调函数、错误监听和页面不存在监听函数等。 详细的参数含义和使…...

编程日记 2023/8/23 5:14:13

多种方法实现 Nginx 隐藏式跳转（隐式URL，即浏览器 URL 跳转后保持不变）

多种方法实现 Nginx 隐藏式跳转（隐式URL，即浏览器 URL 跳转后保持不变）。 一个新项目，后端使用 PHP 实现，前端不做路由，提供一个模板，由后端路由控制。 Route::get(pages/{name}, [\App\Http\Controllers\ResourceController::class, getResourceVersion])...

编程日记 2023/8/23 5:13:11

视频汇聚云平台EasyCVR视频监控管理平台进行SDN转推的操作步骤

视频汇聚/视频云存储/集中存储/视频监控管理平台EasyCVR能在复杂的网络环境中&#xff0c;将分散的各类视频资源进行统一汇聚、整合、集中管理&#xff0c;实现视频资源的鉴权管理、按需调阅、全网分发、云存储、智能分析等&#xff0c;视频智能分析平台EasyCVR融合性强、开放度…...

编程日记 2023/8/23 5:12:09

SQL 语句继续学习之记录二

三&#xff0c; 聚合与排序 对表进行聚合查询&#xff0c;即使用聚合函数对表中的列进行合计值或者平均值等合计操作。 通常&#xff0c;聚合函数会对null以外的对象进行合计。但是只有count 函数例外&#xff0c;使用count(*) 可以查出包含null在内的全部数据行数。 使用dis…...

编程日记 2023/8/23 5:11:07

【Python原创设计】基于Python Flask 机器学习的全国+上海气象数据采集预测可视化系统-附下载链接以及详细论文报告，原创项目其他均为抄袭

基于Python Flask 机器学习的全国上海气象数据采集预测可视化系统 一、项目简介二、开发环境三、项目技术四、功能结构五、运行截图六、功能实现七、数据库设计八、源码获取 一、项目简介 在信息科技蓬勃发展的当代&#xff0c;我们推出了一款基于Python Flask的全国上海气象数…...

编程日记 2023/8/23 5:10:05

Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四)

文章目录 Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四)服务端客户端 Unity进阶–通过PhotonServer实现人物选择和多人同步–PhotonServer(四) 服务端 服务端结构如下&#xff1a; UserModel using System; using System.Collections.Generic; usin…...

编程日记 2023/8/23 5:09:04

【Go 基础篇】Go语言获取用户终端输入：实现交互式程序的关键一步

介绍 在许多编程场景中&#xff0c;我们需要编写交互式程序&#xff0c;以便用户可以在终端中输入数据并与程序进行交互。Go语言提供了丰富的方式来获取用户终端输入&#xff0c;使得编写交互式程序变得简单而有趣。本篇博客将深入探讨Go语言中获取用户终端输入的各种方法&…...

编程日记 2023/8/23 5:08:00

学习笔记：Opencv实现拉普拉斯图像锐化算法

2023.8.19 为了在暑假内实现深度学习的进阶学习&#xff0c;Copy大神的代码&#xff0c;记录学习日常 图像锐化的百科&#xff1a; 图像锐化算法-sharpen_lemonHe_的博客-CSDN博客 在环境配置中要配置opencv&#xff1a; pip install opencv-contrib-python Code and lena.png…...

编程日记 2023/8/23 5:06:54

如何在前端实现WebSocket发送和接收UDP消息（多线程模式）

目录 简介&#xff1a;步骤1&#xff1a;创建WebSocket连接步骤2&#xff1a;创建Web Workers步骤3&#xff1a;发送和接收UDP消息&#xff08;多线程模式&#xff09;结束语&#xff1a; 简介&#xff1a; 本文将继续介绍如何在前端应用中利用WebSocket技术发送和接收UDP消息…...

编程日记 2023/8/23 5:05:49

【微服务】一文了解 Nacos

一文了解 Nacos Nacos 在阿里巴巴起源于 2008 2008 2008 年五彩石项目&#xff08;完成微服务拆分和业务中台建设&#xff09;&#xff0c;成长于十年双十一的洪峰考验&#xff0c;沉淀了简单易用、稳定可靠、性能卓越的核心竞争力。 随着云计算兴起&#xff0c; 2018 2018 20…...

编程日记 2023/8/23 5:04:48

量子计算对信息安全的影响：探讨量子计算技术对现有加密方法和信息安全基础设施可能带来的颠覆性影响，以及应对策略

第一章&#xff1a;引言 随着科技的迅猛发展&#xff0c;量子计算作为一项颠覆性的技术正逐渐走入我们的视野。量子计算以其强大的计算能力引发了全球科技界的广泛关注。然而&#xff0c;正如硬币的两面&#xff0c;量子计算技术所带来的不仅仅是计算能力的巨大飞跃&#xff0…...

编程日记 2023/8/23 5:03:46

ajax-axios-url-form-serialize 插件

AJAX AJAX 概念 1.什么是 AJAX ? mdn 使用浏览器的 XMLHttpRequest 对象 与服务器通信 浏览器网页中&#xff0c;使用 AJAX技术&#xff08;XHR对象&#xff09;发起获取省份列表数据的请求&#xff0c;服务器代码响应准备好的省份列表数据给前端&#xff0c;前端拿到数据数…...

编程日记 2023/8/23 5:02:45

【AIGC】单图换脸离线版软件包及使用方法

云端再好&#xff0c;都不如放自己手里啊&#xff0c;想怎么就怎么玩。云端再好&#xff0c;都不如放自己手里啊&#xff0c;想怎么就怎么玩。 Roop作为一个新出的开源项目&#xff0c;配置起来还是有一定难度的。 我已经把各种依赖&#xff0c;模型&#xff0c;环境配置已经…...

编程日记 2023/8/23 5:01:43

8.19论文阅读

文章目录 Graph-Segmenter: Graph Transformer with Boundary-aware Attention for Semantic Segmentation方法 SCSC: Spatial Cross-scale Convolution Module to Strengthen both CNNs and Transformers方法 Deformable Mixer Transformer with Gating for Multi-Task Learni…...

编程日记 2023/8/23 5:00:41

HAProxy

目录 HAProxy HAProxy介绍 主要特性 LVS、nginx、HAProxy区别 nginx LVS HAProxy 负载均衡策略 Haproxy搭建 Web 群集 Haproxy服务器 编译安装 Haproxy Haproxy服务器配置 添加haproxy 系统服务 节点服务器部署 日志定义 HAProxy HAProxy介绍 HAProxy是可提供高…...

编程日记 2023/8/23 4:59:35

基于EasyExcel的Excel读取

1.引入依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.11</version> </dependency>2.读取器代码&#xff1a; package com.vz.utils.excel;import com.alibaba.excel.Eas…...

编程日记 2023/8/23 4:58:33

链路聚合详解

链路聚合详解 华为交换机链路聚合&#xff1a;Linux链路聚合bond配置 华为交换机链路聚合&#xff1a; 方式一&#xff1a;配置手工负载分担方式的链路聚合 [CORE1] interface Eth-Trunk 1 [CORE1-Eth-Trunk1] trunkport GigabitEthernet 0/0/5 to 0/0/6 [CORE1-Eth-Trunk1] p…...

编程日记 2023/8/23 4:57:32

Shell编程学习之if分支语句的应用

Shell编程中的if分支语句&#xff1a;伪代码表示&#xff1a;注意符号和表达式之间的空格&#xff1b; if [ 表达式1 ] then分支1 elif [ 表达式2 ] then分支2 elif [ 表达式3 ] then分支3 else其它 fi按整型的方式&#xff0c;if分支语句比较字符串的大小&#xff1a;等于&am…...

编程日记 2023/8/23 4:56:31

2023.8 - java - 泛型

泛型问题的引出&#xff1a; jdk 1.5 引出泛型 // package 泛型; public class index {public static void main (String[] args){test t new test();t.setContent("aaa");int a (int) t.getContent();System.out.println(a);} }class test{Object content;publi…...

编程日记 2023/8/23 4:55:28

【数据结构练习】链表面试题锦集一

目录 前言&#xff1a; 1. 删除链表中所有值为key的节点 方法一&#xff1a;正常删除&#xff0c;头结点另外讨论 方法二:虚拟头结点法 方法三&#xff1a;递归 2.反转链表 方法一&#xff1a;双指针迭代 方法二&#xff1a;递归法解析&#xff1a; 3.链表的中间结点 方法…...

编程日记 2023/8/23 4:54:25

自然语言处理从入门到应用——LangChain：链（Chains）-[通用功能：SequentialChain和TransformationChain]

分类目录&#xff1a;《自然语言处理从入门到应用》总目录 SequentialChain 在调用语言模型之后&#xff0c;下一步是对语言模型进行一系列的调用。若可以将一个调用的输出作为另一个调用的输入时则特别有用。在本节中&#xff0c;我们将介绍如何使用顺序链来实现这一点。顺序…...

编程日记 2023/8/23 4:53:24

什么是卷积神经网络

目录 什么是卷积神经网络 全链接相对笨重&#xff1a;大胖子​编辑 ​编辑 参数众多&#xff1a;容易造成过拟合 ​编辑 卷积核&#xff1a;进行图像特征提取&#xff0c;源于卷积原理&#xff1a;求相交面积 卷积的作用 卷积的意义 ​编辑 通过卷积核减少参数 深度卷积…...

编程日记 2023/8/23 4:52:22

银行数字化转型程度-根据年报词频计算（2012-2021年）

银行数字化转型程度是根据银行年报中的数字化相关词频计算所得的数据。这一数据包括数字化词频关键词、以及数字化转型程度&#xff0c;反映了银行数字化转型的程度和进展情况。从经济学研究的角度来看&#xff0c;这一数据具有重要的参考价值。 首先&#xff0c;银行数字化转…...

编程日记 2023/8/23 4:51:20

微信开发之一键修改群聊备注的技术实现

修改群备注 修改群名备注后&#xff0c;如看到群备注未更改&#xff0c;是手机缓存问题&#xff0c;可以连续点击进入其他群&#xff0c;在点击进入修改的群&#xff0c;再返回即可看到修改后的群备注名&#xff0c;群名称的备注仅自己可见 请求URL&#xff1a; http://域名地…...

编程日记 2023/8/23 4:50:19

[oneAPI] 基于BERT预训练模型的SQuAD问答任务

[oneAPI] 基于BERT预训练模型的SQuAD问答任务 Intel Optimization for PyTorch and Intel DevCloud for oneAPI基于BERT预训练模型的SQuAD问答任务语料介绍数据下载构建 模型 结果参考资料 比赛&#xff1a;https://marketing.csdn.net/p/f3e44fbfe46c465f4d9d6c23e38e0517 Int…...

编程日记 2023/8/23 4:49:17

机器学习笔记之优化算法(十七)梯度下降法在强凸函数的收敛性分析

机器学习笔记之优化算法——梯度下降法在强凸函数的收敛性分析 引言回顾&#xff1a;梯度下降法在强凸函数的收敛性二阶可微——梯度下降法在强凸函数的收敛性推论 引言 上一节介绍并证明了&#xff1a;梯度下降法在强凸函数上的收敛速度满足 Q \mathcal Q Q-线性收敛。 本节将…...

编程日记 2023/8/23 4:48:16

shell脚本中linux命令的特殊用法记录

shell脚本中linux命令的特殊用法记录 1、linux命令特殊参数选项1.1、sed -e1.2、echo -e 2、 shell 扩展2.1、[[ ]]支持用~进行正则匹配 3、特殊命令用法3.1、{} 变量替换 1、linux命令特殊参数选项 1.1、sed -e sed -e以严格模式执行脚本&#xff0c;在sed -e 后面的所有命令…...

编程日记 2023/8/23 4:47:14

Nvidia H100：今年55万张够用吗？

原文标题&#xff1a;Nvidia H100: Are 550,000 GPUs Enough for This Year? 作者&#xff1a;Doug Eadline August 17, 2023 The GPU Squeeze continues to place a premium on Nvidia H100 GPUs. In a recent Financial Times article, Nvidia reports that it expects to…...

编程日记 2023/8/23 4:46:12

【Vue2.0源码学习】生命周期篇-初始化阶段(initLifecycle)

文章目录 1. 前言2. initLifecycle函数分析3. 总结 1. 前言 在上篇文章中&#xff0c;我们介绍了生命周期初始化阶段的整体工作流程&#xff0c;以及在该阶段都做了哪些事情。我们知道了&#xff0c;在该阶段会调用一些初始化函数&#xff0c;对Vue实例的属性、数据等进行初始…...

编程日记 2023/8/23 4:45:11

Android开发基础知识总结（三）简单控件（上）

一.文本显示 考虑到结构样式相分离的思想&#xff0c;我们往往在XML中设置文本 <TextViewandroid:layout_width"342dp"android:layout_height"70dp"android:text"房价计算器"android:layout_gravity"center"android:textColor"…...

编程日记 2023/8/23 4:44:10

在Qt窗口中添加右键菜单

在Qt窗口中添加右键菜单 基于鼠标的事件实现流程demo 基于窗口的菜单策略实现Qt::DefaultContextMenuQt::ActionsContextMenuQt::CustomContextMenu信号API 基于鼠标的事件实现 流程 需要使用:事件处理器函数(回调函数) 在当前窗口类中重写鼠标操作相关的的事件处理器函数&a…...

编程日记 2023/8/23 4:43:08

Day8 智慧商城

项目演示 项目收获 创建项目 调整初始化目录 1.删components里的所有文件 2.删views里的所有文件 3.router/index.js 删路由 删规则 import Vue from vue import VueRouter from vue-routerVue.use(VueRouter)const router new VueRouter({routes: [] })export default route…...

编程日记 2023/8/23 4:42:05

LeetCode：Hot100python版本之回溯

回溯算法其实是纯暴力搜索。for循环嵌套是写不出的 组合&#xff1a;没有顺序 排列&#xff1a;有顺序 回溯法可以抽象为树形结构。只有在回溯算法中递归才会有返回值。 46. 全排列 排列是有顺序的。 组合类问题用startindex&#xff0c;排序类问题用used&#xff0c;来标…...

编程日记 2023/8/23 4:41:04