[LeetCode周赛复盘] 第 333 场周赛20230219
[LeetCode周赛复盘] 第 333 场周赛20230219
- 一、本周周赛总结
- 二、 [Easy] 6362. 合并两个二维数组 - 求和法
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、[Medium] 6365. 将整数减少到零需要的最少操作数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、[Medium] 6364. 无平方子集计数
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、[Hard] 6363. 找出对应 LCP 矩阵的字符串
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- 滑铁卢之战,以为要1题下班了,最后做出了T2,后两道不会做,一次掉80分,排名两千多。
- T1 模拟。
- T2 记忆化搜索 / dp。
- T3 子集状压DP/背包。
- T4 构造/思维题。

二、 [Easy] 6362. 合并两个二维数组 - 求和法
链接: 6362. 合并两个二维数组 - 求和法
1. 题目描述
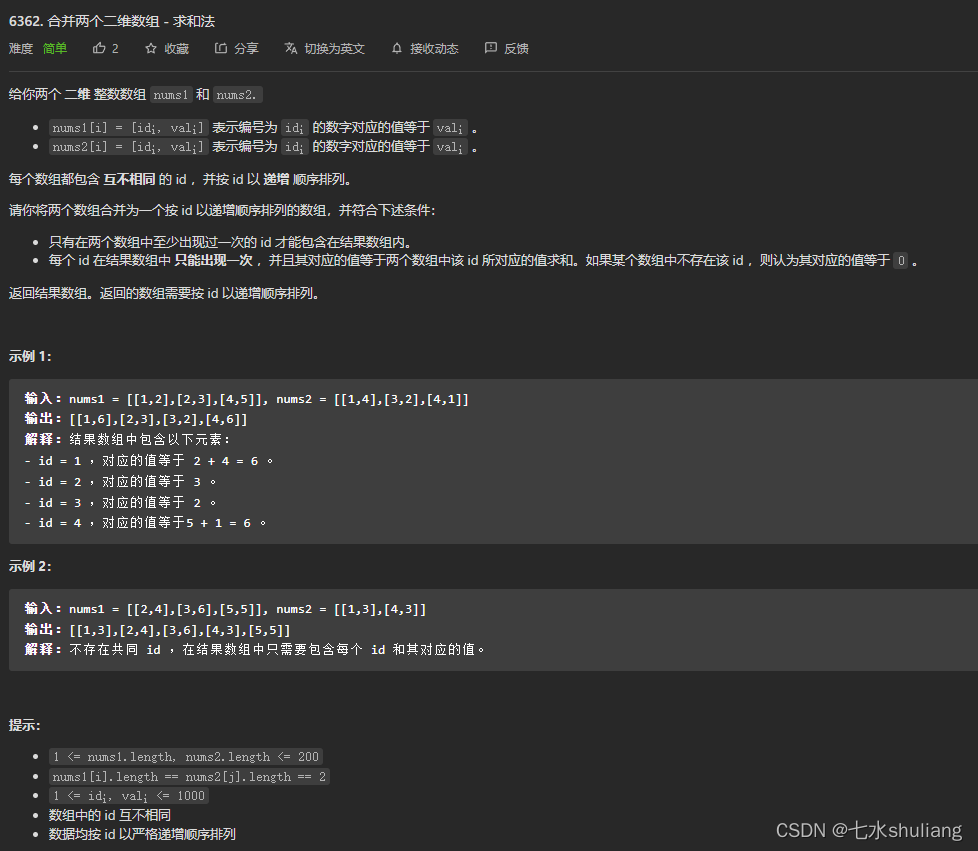
2. 思路分析
- 实际上题目考察归并排序,但是直接排序写得快。
3. 代码实现
class Solution:def mergeArrays(self, nums1: List[List[int]], nums2: List[List[int]]) -> List[List[int]]:cnt = Counter()for x,y in (nums1+nums2):cnt[x] += y return sorted([[k,v] for k,v in cnt.items()])
三、[Medium] 6365. 将整数减少到零需要的最少操作数
链接: 6365. 将整数减少到零需要的最少操作数
1. 题目描述

2. 思路分析
比赛时写了非常麻烦的两次DP。但都是在二进制串上dp的,因此复杂度是O(lgn)
- 把二进制串写出来,然后对连续的1分组,发现规律,如果是单独一个1可以直接1步减去,否则可以加lowbit然后1减去。
- 如果两组之间相隔仅1个0,可以尝试把这个0变成1,然后这两组一起加lowbit减去,共3步;但考虑到上一步已计算,因此这步多了2步,可以指直接讨论。
灵神的lowbit思路
- 从前往后讨论的比较复杂,其实从后往前讨论更方便一些,只需要考虑lowbit的加减即可。
3. 代码实现
记忆化搜索
@cache
def dfs(x):if x.bit_count() == 1:return 1lb = x & -x return 1 + min(dfs(x+lb),dfs(x-lb))
class Solution:def minOperations(self, n: int) -> int:return dfs(n)
dp
class Solution:def minOperations(self, n: int) -> int:s = bin(n)[2:]n = len(s)f = [0]*nf[0] = 1for i in range(1,n):if s[i] == '1':f[i] = f[i-1] + 1x = []p = 0for i,v in enumerate(f):if v == 0 and p != -1:x.append((p,i-1))p = -1if v == 1:p = iif p != -1:x.append((p,n-1))ans = [x[0][1]-x[0][0]+1,2]p = -2for i in range(1,len(x)):l,r = x[i]f = [0,0]f[0] = min(ans) + r-l+1f[1] = min(ans)+2if l - x[i-1][1] == 2:f[1] = min(f[1],ans[1]+1)ans = freturn min(ans)
四、[Medium] 6364. 无平方子集计数
链接: 6364. 无平方子集计数
1. 题目描述

2. 思路分析
- 这题是状压dp,比赛时想到了,但不会写。
- 其实灵神叫它:子集型状压DP。也就是枚举子集。
- 由于题目值域1~30很小,之间的质数共有10个可以先枚举出来,用10位来表示这10个质数是否被使用了。
- 然后对这30个数标记可以用的,再组合这些可以用的数,即合法的子集,求方案数。
- 状态就是哪些质数集合组成的乘积,它的方案数。
- 用刷表法转移:当处理一个合法数字时,若一个状态可以容纳这个数,那么组成的更大状态应该加上小状态的方案数。
- 这题里还学到了如何快速枚举mask子集,包括是否枚举空集的情况。
s = p # 枚举p的子集,不包含空集
while s:s = (s-1)&p
s = p # 枚举p的子集,包含空集
while True: s = (s-1)&pif s == p:break
3. 代码实现
PRIMES = 2,3,5,7,11,13,17,19,23,29
NSQ_TO_MASK = [0]*31 # 把2-30每个数都转化成它的质因子表示的位掩码
for i in range(2,31):for j, p in enumerate(PRIMES):if i % p == 0:if i%(p*p) == 0: # 如果含有平方因子则标记为否NSQ_TO_MASK[i] = -1breakNSQ_TO_MASK[i] |= 1<<j
MOD = 10**9+7
class Solution:def squareFreeSubsets(self, nums: List[int]) -> int:cnt = Counter(nums) # 计数M = 1 << len(PRIMES) # 掩码能组成状态的范围f = [0] * M # 每个状态的种类f[0] = 1 # 空方案数为1for x, c in cnt.items(): # 虽然是全部枚举,但是1的mask是0因此会跳过mask = NSQ_TO_MASK[x] # 取出掩码if mask > 0: # x是nsqother = (M-1)^mask # mask的补集j = other # 下面这一段是标准的枚举other补集(包括空集)的代码while True:f[j|mask] += f[j]*c # 补集加j的状态数应该累加上j的状态数f[j|mask] %= MOD j = (j-1)&otherif j == other:break # 由于是含空集,j会到0然后-1(二进制是全集),&other就==otherans = sum(f)*pow(2,cnt[1],MOD) - 1 # -1去掉空集return ans % MOD
五、[Hard] 6363. 找出对应 LCP 矩阵的字符串
链接: 6363. 找出对应 LCP 矩阵的字符串
1. 题目描述
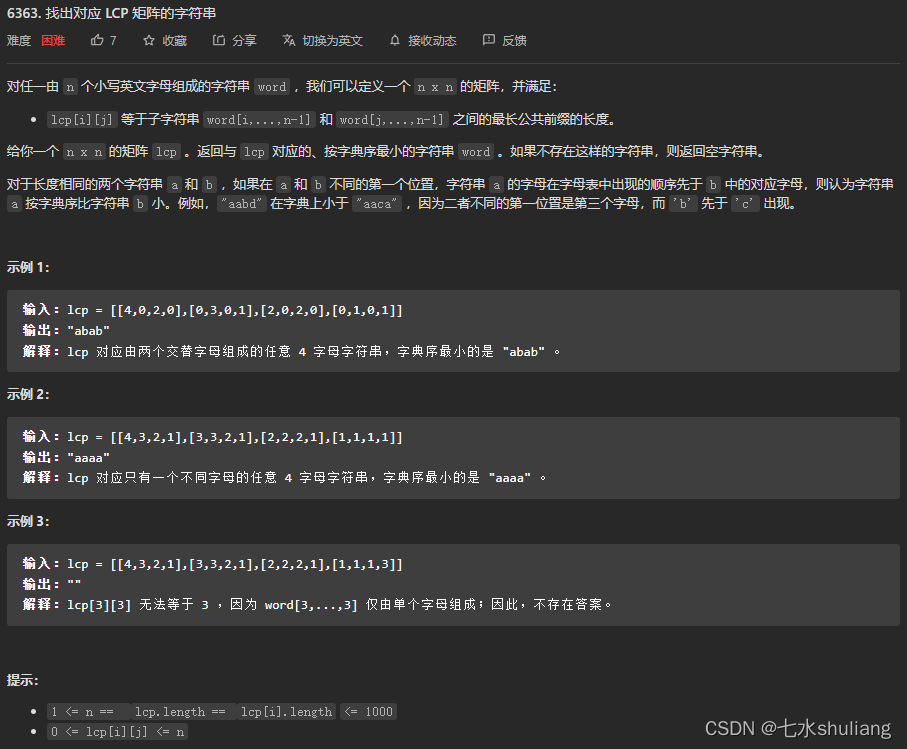
2. 思路分析
一道艰难的思维构造题。
- 首先s[0]肯定是a,否则造不出来答案。
- 并且所有lcp[i][j]不为0的位置,s[i] == s[j]。
- 所有位0的位置,字符必不可以相同。
- 那么从左到右填字符,优先填’a’,看lcp[0],即第一行,哪个数>0,则那个j也必须是a。
- 然后枚举b的位置,也从左做导游选第一个没填的位置;后续同理。
- 枚举完检查是否没填完,但字符用完了,就不合法。
- 最后在s中验证lcp数组,合法就返回s。
3. 代码实现
class Solution:def findTheString(self, lcp: List[List[int]]) -> str:n = len(lcp)s = [''] * n i = 0for c in ascii_lowercase: # 优先用小的字母while i < n and s[i]: # 找到还没填的位置i += 1if i == n:break s[i] = c # 直接填for j in range(i+1,n): # 和这个位置相同的位置都要填它if lcp[i][j]:s[j] = c if '' in s: # 如果字母都用完了还没填完就失败return ''# 在原数组上验证for i in range(n-1,-1,-1):for j in range(n-1,-1,-1):if s[i] == s[j]:if i == n-1 or j == n-1:if lcp[i][j] != 1:return ''else:if lcp[i][j] != lcp[i+1][j+1] + 1:return ''else:if lcp[i][j]:return ''return ''.join(s)
六、参考链接
相关文章:

[LeetCode周赛复盘] 第 333 场周赛20230219
[LeetCode周赛复盘] 第 333 场周赛20230219 一、本周周赛总结二、 [Easy] 6362. 合并两个二维数组 - 求和法1. 题目描述2. 思路分析3. 代码实现三、[Medium] 6365. 将整数减少到零需要的最少操作数1. 题目描述2. 思路分析3. 代码实现四、[Medium] 6364. 无平方子集计数1. 题目描…...
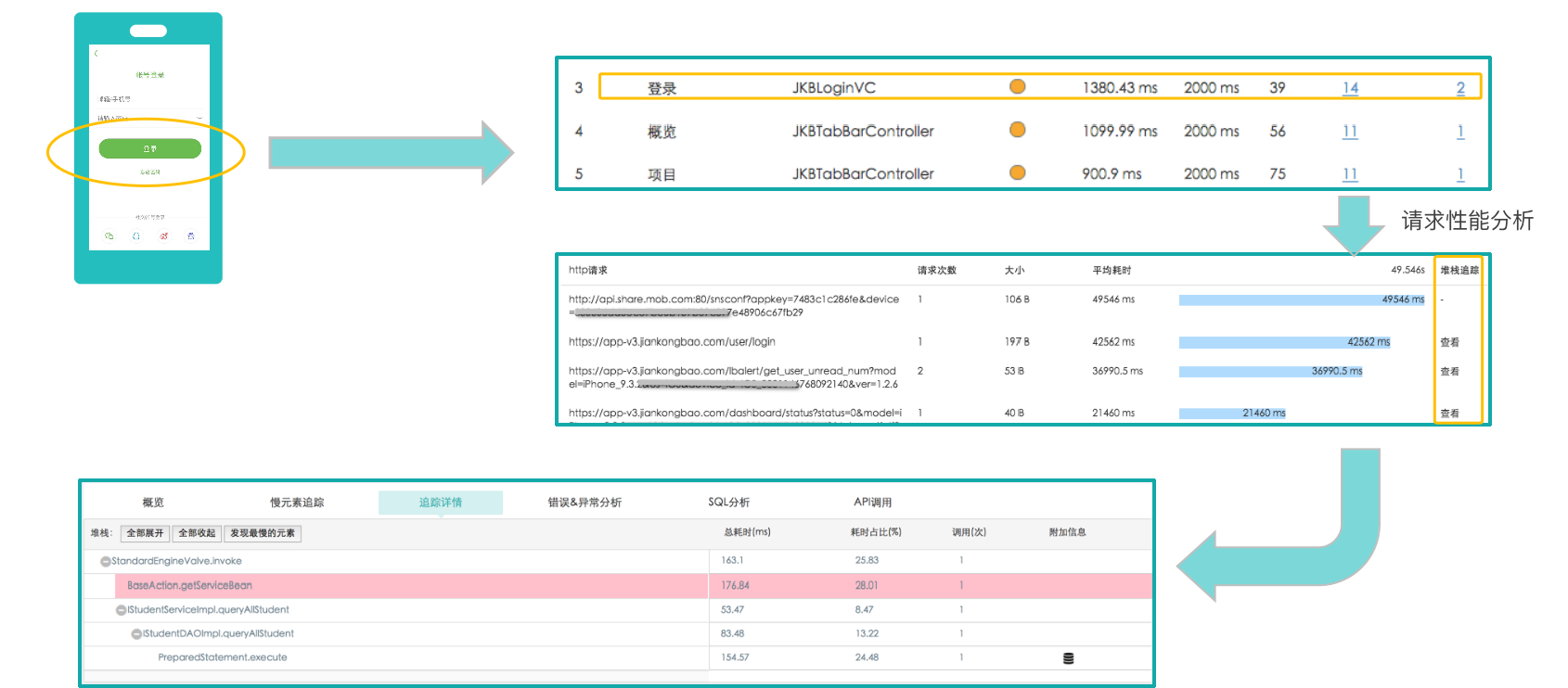
数字化时代,如何做好用户体验与应用性能管理
引言 随着数字化时代的到来,各个行业的应用系统从传统私有化部署逐渐转向公有云、行业云、微服务,这种变迁给运维部门和应用部门均带来了较大的挑战。基于当前企业 IT 运维均为多部门负责,且使用多种运维工具,因此,当…...

Python爬虫(7)selenium3种弹窗定位后点击操作,解决点击登录被隐藏iframe无法点击的登陆问题
之前的文章有关于更多操作方式详细解答,本篇基于前面的知识点进行操作,如果不了解可以先看之前的文章 Python爬虫(1)一次性搞定Selenium(新版)8种find_element元素定位方式 Python爬虫(2)-Selenium控制浏览…...

如何对项目健康度进行测量?评估项目健康状况
项目驱动变革,大部分公司逐步由运营驱动转变为项目驱动,带来更多重新和商业价值。对组织而言,从商业角度看,项目旨在推动组织从一个状态转到另一个状态,从而达成特定目标。项目的健康情况如何关乎项目和变革的成本&…...

美国原装二手keysight E4980A(安捷伦)2MHZ LCR表
Agilent E4980A、Keysight E4980A、LCR 表,20 Hz - 2 MHz E4980A 是 Agilent 的 2 MHz LCR 表。LCR表是一种电子测试设备,用于测量电子元件的电感(L)、电容(C)和电阻(R)。LCR 表可…...

《clean coder》:关于摆烂,争论和心态
“凡是不能在五分钟之内解决的争论,都不能依靠辩论解决” ---- Kent Beck 作为一个码农,我并不是一个喜欢争论的角色。很长一段时间会陷入一种摆烂的,被动的状态。“既然其他人想要这么做,就这么办吧”。这可能是非专业的行为中最…...
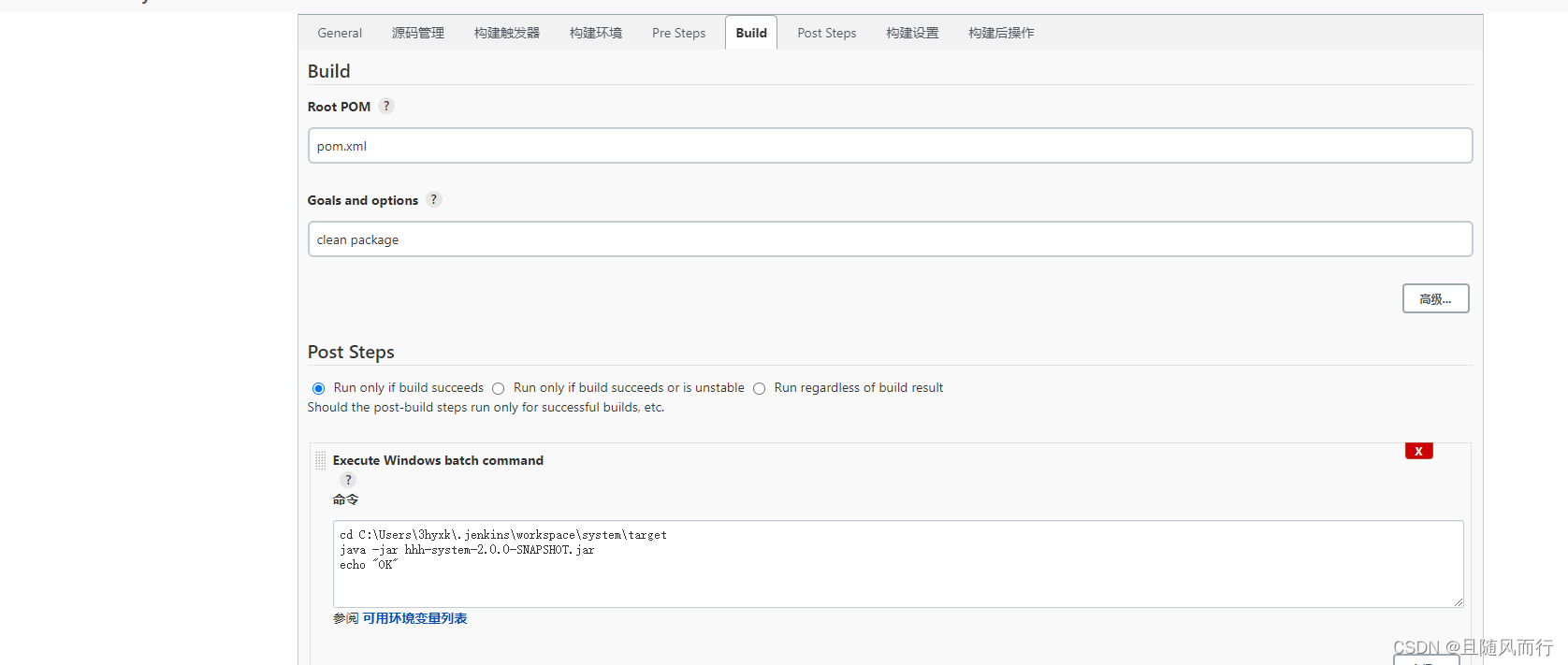
jenkins下载与简单使用
1.jenkins下载 因为我仍然使用的是jdk1.8进行开发,所以我下载的是jenkins2.332.1版本(jenkins2.346.1版本在2022年末不再支持java8,如果项目使用的是jdk11可以继续使用该jenkins版本),更多版本下载请点击jenkins下载 …...

3|物联网控制|计算机控制-刘川来胡乃平版|第3章:计算机总线技术 补充串行总线部分|课堂笔记|ppt
2022年 10月 10日 3.3 外部总线 3.3.2 RS-232-C总线 机械特性...

Blazor入门100天 : 身份验证和授权 (3) - DB改Sqlite
目录 建立默认带身份验证 Blazor 程序角色/组件/特性/过程逻辑DB 改 Sqlite将自定义字段添加到用户表脚手架拉取IDS文件,本地化资源freesql 生成实体类,freesql 管理ids数据表初始化 Roles,freesql 外键 > 导航属性完善 freesql 和 bb 特性 本节源码 https://github.com/…...

阅读源码和查看官方文档,是解决问题最高效的办法。
作为一个工作8年的老程序员告诉你:阅读源码和查看官方文档,是解决问题最高效的办法。不信你来看,这个困扰了读者半天的问题我查了源码和文档后瞬间解决。 前言 上周五有位读者私信我一个问题,说困扰了他半天,研究了一…...

云原生流量管理系统中 Service , Ingress 和 Endpoint 的关系
摘要 Kubernetes(简称 K8s)是一个用于容器编排和管理的开源平台,其中流量管理是 K8s 的重要功能之一。K8s 提供了多种流量管理方式,以便对不同场景下的流量进行控制和管理。以下是 K8s 中常用的流量管理系统: Service:Service 是 K8s 中最基本的流量管理方式,用于提供…...

给你安利几款好用的谷歌浏览器插件
给你安利几款好用的谷歌浏览器插件前言一 Octotree 插件二 GitCodeTree 插件三 SourceGraph 插件四 GitZip 插件五 Enhanced GitHub 插件六 插件下载安装6.1 谷歌应用商店下载6.2 离线安装6.2.1 下载插件6.2.2 安装插件七 移除、启用、停用插件小结前言 GitHub是全球最大的代码…...
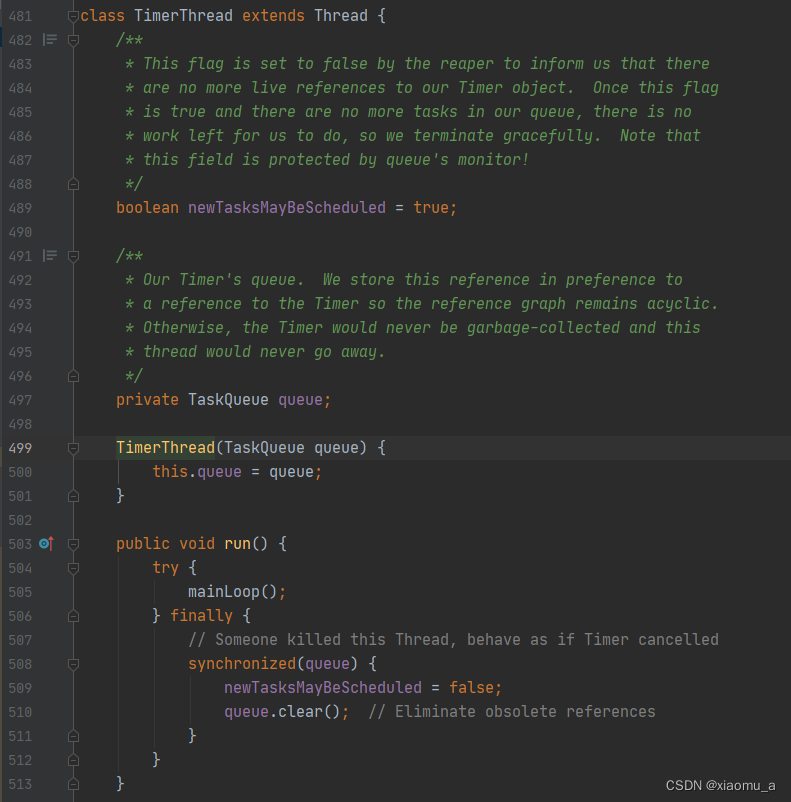
JDK定时器Timer原理
前言 前些时间想到利用redis实现延时队列,但是底层的定时器不止如何实现好些,故此研究了一下jdk的Timer。 Timer是一个用于执行定时任务的类,可以单次执行或按指定时间间隔循环执行(直到主动cancel或线程被杀掉)。Ti…...

vue3中使用swiper完整版教程
介绍 在 vue3 中使用 swiper, 实现轮播图的效果;如果组件样式等模块引入不当,很有可能导致,页面无效果;或者想要的箭头或者切换效果异常问题。具体使用方式如下所示: 使用方式 使用命令 npm install swiper 安装 sw…...

某个div的滚动条样式
.item-body,.chart2{/*滚动条整体样式*/&::-webkit-scrollbar {/*高宽分别对应横竖滚动条的尺寸*/width: 10px;height: 1px;}/*滚动条里面小方块*/&::-webkit-scrollbar-thumb {border-radius: 10px;-webkit-box-shadow: inset 0 0 5px rgba(0, 0, 0, 0.2);background:…...
Spring Boot框架基础介绍
Spring Boot 是一款基于 Spring 框架的开源应用程序开发工具,它旨在简化 Spring 应用程序的配置和开发过程。Spring Boot 提供了一种简单的方式来创建可独立运行的、生产级别的应用程序,并在需要时进行部署。Spring Boot 在微服务架构和云计算环境下得到…...
Git - 在主分支上创建分支并提交代码
拉取最新代码 因为当前在 master 分支下,你必须拉取最新代码,保证当前代码与线上同步(最新),执行以下命令: git pull origin master创建分支 目前我们在 master 主分支上,需要执行以下命令&…...

第三届无线通信AI大赛分享交流会暨颁奖典礼顺利举办,大赛圆满收官
2月16日,第三届无线通信AI大赛分享交流会暨颁奖典礼在北京顺利举行,宣告大赛圆满收官。 分享交流会暨颁奖典礼以线上线下结合的形式展开,邀请无线通信领域的多位专家、学者与「基于AI的信道估计与信道状态信息反馈联合设计」、「基于AI的高精…...

程序的本质与类的说明
摘自《深入浅出WPF完整版》P132程序的本质就是“数据算法”,,这一本质一直没有改变一一类的作用只是把散落在程序中的变量和函数进行归档封装并控制对它们的访问而已。被封装在类里的变量称为字段 (Fied)它表示的是类或实例的状态:被封装在类里的函数称为…...
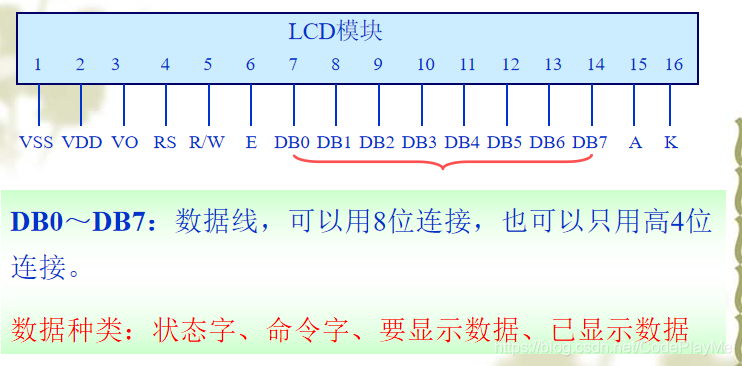
单片机——显示方式
数码LED 一、静态显示方式 1、连接 所有LED的位选均共同连接到VCC或GND,每个LED的8根段选线分别连接一个8位并行I/O口,从该I/O口送出相应的字型码显示字型。 2、这种连接方式的缺点就是需要的数据线太多:我们可以计算一下:8*4133根…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
