西瓜书第三章
广义线性模型
考虑单点可微函数 g ( ⋅ ) g(\cdot) g(⋅),令 y = g − 1 ( ω T x + b ) y=g^{-1}(\omega^{T}x+b) y=g−1(ωTx+b),这样得到的模型称为“广义线性模型”,其中函数 g ( ⋅ ) g(\cdot) g(⋅)称为“联系函数”。显然,对数线性回归是广义线性模型在 g ( ⋅ ) = ln ( ⋅ ) g(\cdot)=\ln (\cdot) g(⋅)=ln(⋅)时的特例。
对数几率回归
在线性回归模型的基础上,改进以完成分类任务。关键在于寻找一个单调可微函数,将分类任务的真实标记 y y y与线性回归模型的预测值联系起来。
考虑二分类任务
y ∈ { 0 , 1 } ⇔ z = ω T x + b y\in \{0,1\}\Leftrightarrow z=\omega^Tx+b y∈{0,1}⇔z=ωTx+b
于是,我们需将实值z转换为0/1值。
- 单位跃阶函数:
y = { 0 , z < 0 0.5 , z = 0 1 , z > 0 y= \left\{ \begin{aligned} 0,\quad z<0\\ 0.5,\quad z=0\\ 1,\quad z>0 \end{aligned} \right. y=⎩ ⎨ ⎧0,z<00.5,z=01,z>0
单位跃阶函数不连续,从而不可微,故不能直接作为联系函数。 - 对数几率函数
y = 1 1 + e − z y=\frac{1}{1+e^{-z}} y=1+e−z1
对数几率函数是一种Sigmoid函数。
Sigmoid函数即形似S的函数,对率函数是Sigmoid函数最重要代表。
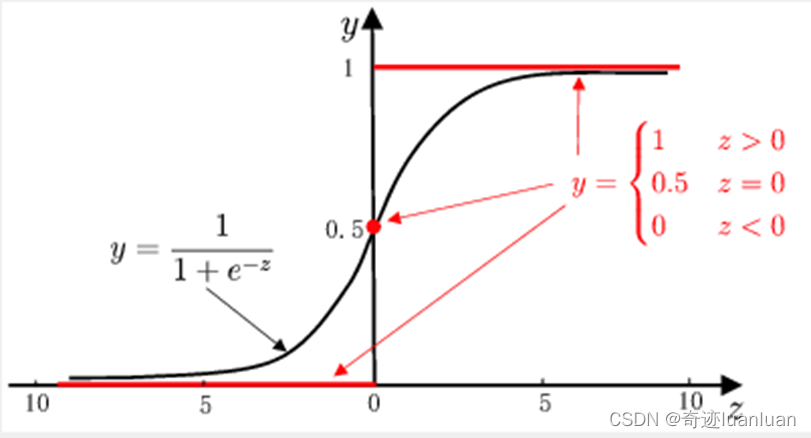
代入广义线性模型中得到
y = 1 1 + e − ( ω T x + b ) = e ω T x + b 1 + e ω T x + b 1 − y = e − ( ω T x + b ) 1 + e − ( ω T x + b ) = 1 1 + e ω T x + b y 1 − y = e ω T x + b ln y 1 − y = ω T x + b \begin{aligned} &y=\frac{1}{1+e^{-(\omega^{T}x+b)}}=\frac{e^{\omega^Tx+b}}{1+e^{\omega^Tx+b}} \\ &1-y=\frac{e^{-(\omega^Tx+b)}}{1+e^{-(\omega^Tx+b)}}=\frac{1}{1+e^{\omega^Tx+b}}\\ &\frac{y}{1-y}=e^{\omega^Tx+b}\\ &\ln \frac{y}{1-y}=\omega^Tx+b \end{aligned} y=1+e−(ωTx+b)1=1+eωTx+beωTx+b1−y=1+e−(ωTx+b)e−(ωTx+b)=1+eωTx+b11−yy=eωTx+bln1−yy=ωTx+b
若将y视为样本x作为正例的可能性,则1-y为样本x为反例的可能性,两者的比值 y 1 − y \frac{y}{1-y} 1−yy称为“几率”,反映了样本x作为正例的可能性。对几率取对数则得到“对数几率”: ln y 1 − y \ln \frac{y}{1-y} ln1−yy。
l n y 1 − y = ω T x + b ln \frac{y}{1-y}=\omega^Tx+b ln1−yy=ωTx+b
实际上是用线性回归模型的预测结果去逼近真实的对数几率,因此该模型也称为“对数几率回归”。(虽然名字叫做回归,但实际上是一种分类学习方法)
对数几率回归的优点
- 它是直接对分类的可能性进行建模,无需事先假设数据的分布,这样就避免了假设分布不准确所带来的问题。
- 它不仅预能预测出类别,而是可以得到近似概率预测,这对许多需要利用概率辅助决策的任务很有用。
- 对率函数是任意阶可导的凸函数,有很好的数学性质,现有的很多数值优化算法都可以直接用于求取最优解。
求解对率回归模型中的参数
将y视为类后验概率估计 p ( y = 1 ∣ x ) p(y=1|x) p(y=1∣x),则对率函数可重写为 ln p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) = ω T x + b \ln \frac{p(y=1|x)}{p(y=0|x)}=\omega^Tx+b lnp(y=0∣x)p(y=1∣x)=ωTx+b
由于 p ( y = 1 ∣ x ) + p ( y = 0 ∣ x ) = 1 p(y=1|x)+p(y=0|x)=1 p(y=1∣x)+p(y=0∣x)=1,从而有 y = p ( y = 1 ∣ x ) = e ω T x + b 1 + e ω T x + b 1 − y = p ( y = 0 ∣ x ) = 1 1 + e ω T x + b \begin{aligned} y=p(y=1|x)=\frac{e^{\omega^Tx+b}}{1+e^{\omega^Tx+b}} \\ 1-y=p(y=0|x)=\frac{1}{1+e^{\omega^Tx+b}} \end{aligned} y=p(y=1∣x)=1+eωTx+beωTx+b1−y=p(y=0∣x)=1+eωTx+b1于是可以通过极大似然法来估计 ω \omega ω和 b b b。给定数据集 { ( x i , y i ) } i = 1 m \{(x_i,y_i)\}_{i=1}^m {(xi,yi)}i=1m,对率回归模型最大化“对数似然”
l ( ω ; b ) = ∑ i = 1 m ln p ( y i ∣ x i ; ω , b ) l(\omega;b)=\sum_{i=1}^m{\ln p(y_i|x_i;\omega,b)} l(ω;b)=i=1∑mlnp(yi∣xi;ω,b)即令每个样本属于其真实标记的概率越大越好。为了便于讨论,令 β = ( ω ; b ) , x ^ = ( x ; 1 ) \beta=(\omega;b),\quad \hat{x}=(x;1) β=(ω;b),x^=(x;1),则 ω T x + b \omega^Tx+b ωTx+b可以简写为 β T x ^ \beta^T\hat{x} βTx^。再令 p 1 ( x ^ ; β ) = p ( y = 1 ∣ x ^ ; β ) , p 0 ( x ^ ; β ) = p ( y = 0 ∣ x ^ ; β ) = 1 − p 1 ( x ^ ; β ) p_1(\hat{x};\beta)=p(y=1|\hat{x};\beta),p_0(\hat{x};\beta)=p(y=0|\hat{x};\beta)=1-p_1(\hat{x};\beta) p1(x^;β)=p(y=1∣x^;β),p0(x^;β)=p(y=0∣x^;β)=1−p1(x^;β),则上式中的似然项可重写为 p ( y i ∣ x i ; ω , b ) = y i p 1 ( x ^ i ; β ) + ( 1 − y i ) p 0 ( x ^ i ; β ) p(y_i|x_i;\omega,b)=y_ip_1(\hat{x}_i;\beta)+(1-y_i)p_0(\hat{x}_i;\beta) p(yi∣xi;ω,b)=yip1(x^i;β)+(1−yi)p0(x^i;β),进一步代入得
l ( ω ; b ) = ∑ i = 1 m ln [ y i p 1 ( x ^ i ; β ) + ( 1 − y i ) p 0 ( x ^ i ; β ) ] = ∑ i = 1 m ln [ y i e ω T x i + b 1 + e ω T x i + b + ( 1 − y i ) 1 1 + e ω T x i + b ] = ∑ i = 1 m ln [ y i e β T x ^ i 1 + e β T x ^ i + ( 1 − y i ) 1 1 + e β T x ^ i ] = ∑ i = 1 m ln [ y i e β T x ^ i − y i + 1 1 + e β T x ^ i ] = ∑ i = 1 m [ ln ( y i e β T x ^ i − y i + 1 ) − ln ( 1 + e β T x ^ i ) ] = ∑ y i = 0 − ln ( 1 + e β T x ^ i ) + ∑ y i = 1 [ ln ( e β T x ^ i ) − ln ( 1 + e β T x ^ i ) ] = − ∑ y i = 0 ln ( 1 + e β T x ^ i ) + ∑ y i = 1 [ β T x ^ i − ln ( 1 + e β T x ^ i ) ] = ∑ i = 1 m [ y i β T x ^ i − ln ( 1 + e β T x ^ i ) ] \begin{aligned} l(\omega;b)&=\sum_{i=1}^m{\ln \left[ y_ip_1(\hat{x}_i;\beta)+(1-y_i)p_0(\hat{x}_i;\beta)\right]}\\ &=\sum_{i=1}^m{\ln \left[y_i\frac{e^{\omega^Tx_i+b}}{1+e^{\omega^Tx_i+b}}+(1-y_i)\frac{1}{1+e^{\omega^Tx_i+b}}\right]}\\ &=\sum_{i=1}^m{\ln \left[y_i\frac{e^{\beta^T\hat{x}_i}}{1+e^{\beta^T\hat{x}_i}}+(1-y_i)\frac{1}{1+e^{\beta^T\hat{x}_i}}\right]}\\ &=\sum_{i=1}^m{\ln \left[\frac{y_ie^{\beta^T\hat{x}_i}-y_i+1}{1+e^{\beta^T\hat{x}_i}}\right]}\\ &=\sum_{i=1}^m{\left[\ln (y_ie^{\beta^T\hat{x}_i}-y_i+1)-\ln (1+e^{\beta^T\hat{x}_i})\right]}\\ &=\sum_{y_i=0}{-\ln (1+e^{\beta^T\hat{x}_i})}+\sum_{y_i=1}{\left[\ln(e^{\beta^T\hat{x}_i})-\ln(1+e^{\beta^T\hat{x}_i})\right]}\\ &=-\sum_{y_i=0}{\ln (1+e^{\beta^T\hat{x}_i})}+\sum_{y_i=1}{\left[\beta^T\hat{x}_i-\ln(1+e^{\beta^T\hat{x}_i})\right]}\\ &=\sum_{i=1}^m{\left[y_i\beta^T\hat{x}_i-\ln(1+e^{\beta^T\hat{x}_i})\right]} \end{aligned} l(ω;b)=i=1∑mln[yip1(x^i;β)+(1−yi)p0(x^i;β)]=i=1∑mln[yi1+eωTxi+beωTxi+b+(1−yi)1+eωTxi+b1]=i=1∑mln[yi1+eβTx^ieβTx^i+(1−yi)1+eβTx^i1]=i=1∑mln[1+eβTx^iyieβTx^i−yi+1]=i=1∑m[ln(yieβTx^i−yi+1)−ln(1+eβTx^i)]=yi=0∑−ln(1+eβTx^i)+yi=1∑[ln(eβTx^i)−ln(1+eβTx^i)]=−yi=0∑ln(1+eβTx^i)+yi=1∑[βTx^i−ln(1+eβTx^i)]=i=1∑m[yiβTx^i−ln(1+eβTx^i)]
从而最大化 l ( ω ; b ) l(\omega;b) l(ω;b)等价于最小化
l ( β ) = ∑ i = 1 m ( − y i β T x ^ i + ln ( 1 + e β T x ^ i ) ) l(\beta)=\sum_{i=1}^m{\left(-y_i\beta^T\hat{x}_i+\ln(1+e^{\beta^T\hat{x}_i})\right)} l(β)=i=1∑m(−yiβTx^i+ln(1+eβTx^i)) l ( β ) l(\beta) l(β)是关于 β \beta β的高阶可导函数,根据凸优化理论,经典的数值优化方法如梯度下降法、牛顿法等都可求得其最优解,于是就得到 β ∗ = a r g m i n β l ( β ) \beta^*=argmin_{\beta}l(\beta) β∗=argminβl(β)
例如牛顿法,其第t+1次轮迭代解的更新公式为
β t + 1 = β t − ( ∂ 2 l ( β ) ∂ β ∂ β T ) − 1 ∂ l ( β ) ∂ β \beta^{t+1}=\beta^{t}-{\left(\frac{\partial^2l(\beta)}{\partial\beta\partial\beta^T}\right)^{-1}\frac{\partial l(\beta)}{\partial\beta}} βt+1=βt−(∂β∂βT∂2l(β))−1∂β∂l(β)
其中关于 β \beta β的一阶、二阶导数分别为
∂ l ( β ) ∂ β = − ∑ i = 1 m x ^ i ( y i − p 1 ( x ^ i ; β ) ) ∂ 2 l ( β ) ∂ β ∂ β T = ∑ i = 1 m x ^ i x ^ i T p 1 ( x ^ i ; β ) ( 1 − p 1 ( x ^ i ; β ) ) \begin{aligned} \frac{\partial l(\beta)}{\partial \beta}&=-\sum_{i=1}^m{\hat{x}_i(y_i-p_1(\hat{x}_i;\beta))}\\ \frac{\partial^2l(\beta)}{\partial\beta\partial\beta^T}&=\sum_{i=1}^m{\hat{x}_i\hat{x}_i^Tp_1(\hat{x}_i;\beta)(1-p_1(\hat{x}_i;\beta))} \end{aligned} ∂β∂l(β)∂β∂βT∂2l(β)=−i=1∑mx^i(yi−p1(x^i;β))=i=1∑mx^ix^iTp1(x^i;β)(1−p1(x^i;β))
【小试牛刀】
编程实现对率回归,并给出西瓜数据集3.0a上的结果。
import numpy as np
import pandas as pd
import xlrd#第一步导入数据
DataSet=pd.read_excel("西瓜数据集3.0a.xlsx")
Data=DataSet.values
#print(Data.shape) #17行4列
X=np.delete(Data,0,1)#在Data的copy基础上删除第一列编号
X=np.delete(X,2,1)
#print(X)
y=Data[:,3]
#print(y)#仍然是ndarray#利用牛顿法求解
def calp1(x,Beta):"""求解样本x在参数beta下取正例的概率p1此处Beta为列向量(3,1),x为列向量(3,1)"""temp=np.exp(np.dot(x.T,Beta))p1=temp/float(1+temp)return p1def calpartial1(X_hat,y,beta):"""求解l(beta)关于参数beta的一阶导数X_hat[i]是行向量,每一行代表一个样本"""m=len(y)partial1=0for i in range(m):x_hat=X_hat[i].reshape(3,1)#把样本x变为列矩阵temp=np.dot(x_hat,y[i]-calp1(x_hat,beta))partial1=partial1+tempreturn -partial1def calpartial2(X_hat,y,beta):"""求解l(beta)关于beta的二阶导数beta为列向量"""m=len(y)partial2=0for i in range(m):x_hat=X_hat[i].reshape(3,1)#把样本x变为列矩阵xxT=np.dot(x_hat,x_hat.T)p1=calp1(x_hat,beta)temp=p1*(1-p1)*xxTpartial2+=tempreturn partial2def LR(X,y,beta,error):"""error为误差"""#在数据集X(每行为一个样本)添加一列1#方法一X_hat=np.insert(X,2,values=1,axis=1)"""col=np.ones((17,1))#创建一个17行1列的元素全为1的二维数组Z=np.c_[X,col]print(Z)"""t=0#迭代次数while t<10000:beta1=beta-np.linalg.inv(calpartial2(X_hat,y,beta)).dot(calpartial1(X_hat,y,beta))if np.linalg.norm(beta-beta1,2)<error:return beta1else:t=t+1beta=beta1print("超过最大迭代次数,认为不收敛!")
np.random.seed(1)
beta=np.random.rand(3,1)
Beta=LR(X,y,beta,1e-5)
print(Beta)
输出:

【编程中注意的一些问题】
- DataSet是Pandas内的对象,决策树的构建需要用到scikit-learn。
Pandas和Scikit-learn没有完美整合,而Numpy和scikit-learn能够很好的协同使用。
从而现将Pandas中的值转化为Numpy,然后再配合scikit-learn工作
numpy中的ndarray为多维数组,是numpy中最为重要也是python进行科学计算非常重要和基本的数据类型。 - numpy矩阵运算大全见这篇博客
numpy中文官网:https://www.numpy.org.cn/reference/
numpy英文官网:https://numpy.org/doc/stable/index.html/
特别注意矩阵乘法:ndarray 是 NumPy 的基础元素,NumPy 又主要是用来进行矩阵运算的.首先,在矩阵用 ±*/ 这些常规操作符操作的时候,是对元素进行操作。这和其他诸如 MATLAB 等语言不一样。 ∗ * ∗并没有进行矩阵乘法,而是矩阵和矩阵的元素进行了相乘。想要进行矩阵乘法计算,需要用dot方法
- numpy.dot()用法:
- numpy.dot()如果处理的是一维数组,则代表向量点积,并且结果与两个参数的位置顺序无关
a1=np.array([1,2,3])
b1=np.array([2,2,2])
print(a1.shape,b1.shape)#(3,) (3,)
print(np.dot(a1,b1),np.dot(b1,a1))#12 12
- numpy.dot()如果处理的是二维数组(矩阵),则代表矩阵乘法
a2=np.arange(3,6,1).reshape(1,3)
print(a2,a2.shape)#[[3,4,5]] (1,3)
b2=np.array([[2,4,6]])
print(b2.shape)#(1,3)
#print(np.dot(b2,a2))#报错
c2=b2.reshape(3,1)
print(c2,c2.shape)
"""
[[2][4][6]] (3,1)
"""
print(np.dot(c2,a2),np.dot(a2,c2))
"""
[[ 6 8 10][12 16 20][18 24 30]] [[52]]
"""
- 标量p与二维数组A相乘时,直接使用p*A
- 向量与二维数组做运算时,不能直接使用numpy.dot()
#解决(3,1)和(3,)在做矩阵积的时候维度不匹配的问题
np.random.seed(1)
a=np.random.randint(1,10,size=(3,1))
print(a.shape)
b=np.append(X[5],[1],0)
print(b)
c=b.reshape(1,3)
print(c)
print(np.dot(a,c))
线性判别分析
线性判别的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,异样样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的直线上,再根据投影点的位置来确定新样本的类别。
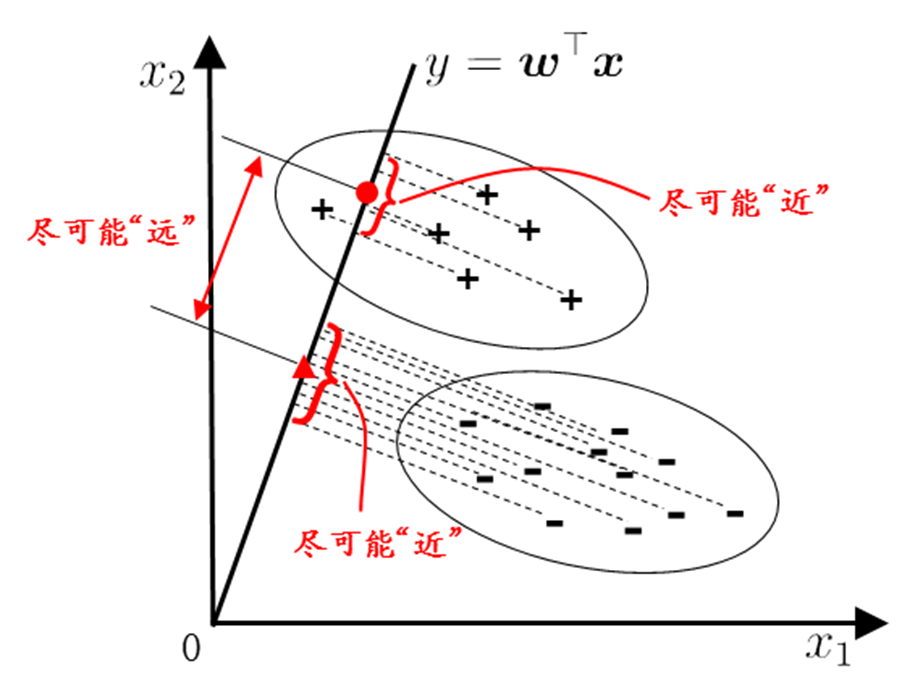
理论推导过程:
数据集: D = { ( x i , y i ) } i = 1 m , y i ∈ { 0 , 1 } , x i ∈ R d D=\{(x_i,y_i)\}_{i=1}^m,y_i\in\{0,1\},x_i\in R^d D={(xi,yi)}i=1m,yi∈{0,1},xi∈Rd
X 0 = { x i ∣ y i = 0 } , X 1 = { x i ∣ y i = 1 } X_0=\{x_i|y_i=0\},X_1=\{x_i|y_i=1\} X0={xi∣yi=0},X1={xi∣yi=1}
设 X i ( i = 0 , 1 ) X_i(i=0,1) Xi(i=0,1)中的样例数量为 n i , n 0 + n 1 = m n_i,n_0+n_1=m ni,n0+n1=m,均值向量为 μ i = ∑ x ∈ X i x \mu_i=\sum_{x\in X_i}x μi=∑x∈Xix,协方差矩阵 Σ i = 1 n i ∑ x j ∈ X i ( x j − μ i ) ( x j − μ i ) T \Sigma_i=\frac{1}{n_i}\sum_{x_j\in X_i}{(x_j-\mu_i)(x_j-\mu_i)^T} Σi=ni1∑xj∈Xi(xj−μi)(xj−μi)T
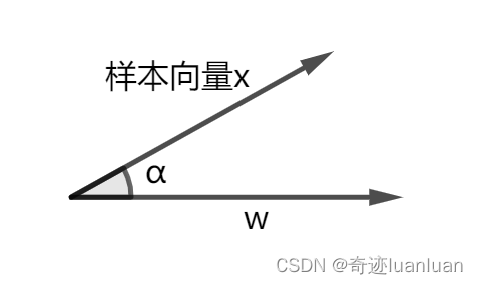
向量x在向量w上的投影 a ( a ∈ R ) a(a\in R) a(a∈R): a = ∣ x ∣ c o s α = ∣ ω ∣ ∣ x ∣ c o s α ∣ o m e g a ∣ = ω T x ∣ ω ∣ a=|x|cos\alpha=\frac{|\omega||x|cos\alpha}{|omega|}=\frac{\omega^Tx}{|\omega|} a=∣x∣cosα=∣omega∣∣ω∣∣x∣cosα=∣ω∣ωTx
则对应的投影向量为 a ω ∣ ω ∣ = ω T x ∣ ω ∣ ω ∣ ω ∣ = ω T x ω ω T ω a\frac{\omega}{|\omega|}=\frac{\omega^Tx}{|\omega|}\frac{\omega}{|\omega|}=\frac{\omega^Tx\omega}{\omega^T\omega} a∣ω∣ω=∣ω∣ωTx∣ω∣ω=ωTωωTxω
容易证明, X i X_i Xi中样例在 ω \omega ω上投影的均值= X i X_i Xi中样例的均值向量在 ω \omega ω上的投影,即 1 n i ∑ x j ∈ X i ω T x j = ω T ( 1 n i ∑ x j ∈ X i x j ) = ω T μ i \frac{1}{n_i}\sum_{x_j\in X_i}\omega^Tx_j=\omega^T(\frac{1}{n_i}\sum_{x_j\in X_i}x_j)=\omega^T\mu_i ni1∑xj∈XiωTxj=ωT(ni1∑xj∈Xixj)=ωTμi
从而将两类样本投影到向量 ω \omega ω上,则两类样本投影点的中心分别为 ω T μ 0 ( μ 0 T ω ) \omega^T\mu_0(\mu_0^T\omega) ωTμ0(μ0Tω)和 ω T μ 1 ( μ 1 T ω ) \omega^T\mu_1(\mu_1^T\omega) ωTμ1(μ1Tω)
两类样本点投影的协方差分别为 X 0 : 1 n 0 ∑ x j ∈ X 0 ( ω T x j − ω T μ 0 ) ( ω T x j − ω T μ 0 ) T 【协方差的计算公式之一】 = 1 n 0 ∑ x j ∈ X 0 ω T ( x i − μ 0 ) ( x i − μ 0 ) T ω = ω T ( 1 n 0 ∑ x j ∈ X 0 ( x i − μ 0 ) ( x i − μ 0 ) T ) ω = ω T Σ 0 ω X 1 : ω T Σ 1 ω 【同理】 \begin{aligned} X_0&:\frac{1}{n_0}\sum_{x_j\in X_0}{(\omega^Tx_j-\omega^T\mu_0)(\omega^Tx_j-\omega^T\mu_0)^T}【协方差的计算公式之一】\\ &=\frac{1}{n_0}\sum_{x_j\in X_0}{\omega^T(x_i-\mu_0)(x_i-\mu_0)^T\omega}\\ &=\omega^T\left(\frac{1}{n_0}\sum_{x_j\in X_0}{(x_i-\mu_0)(x_i-\mu_0)^T}\right)\omega\\ &=\omega^T\Sigma_0\omega\\ X_1&:\omega^T\Sigma_1\omega【同理】 \end{aligned} X0X1:n01xj∈X0∑(ωTxj−ωTμ0)(ωTxj−ωTμ0)T【协方差的计算公式之一】=n01xj∈X0∑ωT(xi−μ0)(xi−μ0)Tω=ωT n01xj∈X0∑(xi−μ0)(xi−μ0)T ω=ωTΣ0ω:ωTΣ1ω【同理】
欲使同类样本点的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小,即 ω T Σ 0 ω + ω T Σ 1 ω \omega^T\Sigma_0\omega+\omega^T\Sigma_1\omega ωTΣ0ω+ωTΣ1ω尽可能小;欲使异类样本的投影点尽可能远离,可以让异类样本点投影后的中心之间的距离尽可能的大,即 ∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 {||\omega^T\mu_0-\omega^T\mu_1||}_2^2 ∣∣ωTμ0−ωTμ1∣∣22尽可能大。 同时考虑二者,可以得到优化目标: J ( ω ) = ∣ ∣ ω T μ 0 − ω T μ 1 ∣ ∣ 2 2 ω T Σ 0 ω + ω T Σ 1 ω = ω T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T ω ω T ( Σ 0 + Σ 1 ) ω \begin{aligned} J(\omega)&=\frac{{||\omega^T\mu_0-\omega^T\mu_1||}_2^2}{\omega^T\Sigma_0\omega+\omega^T\Sigma_1\omega}\\ &=\frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\Sigma_0+\Sigma_1)\omega} \end{aligned} J(ω)=ωTΣ0ω+ωTΣ1ω∣∣ωTμ0−ωTμ1∣∣22=ωT(Σ0+Σ1)ωωT(μ0−μ1)(μ0−μ1)Tω
定义类内散度矩阵 S ω S_{\omega} Sω(与 ω \omega ω无关)
S ω = Σ 0 + Σ 1 S_{\omega}=\Sigma_0+\Sigma_1 Sω=Σ0+Σ1
类间散度矩阵 S b S_b Sb(与 ω \omega ω无关)
S b = ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T Sb=(μ0−μ1)(μ0−μ1)T
此时优化目标可重写为 J ( ω ) = ω T S b ω ω T S ω ω J(\omega)=\frac{\omega^TS_b\omega}{\omega^TS_{\omega}\omega} J(ω)=ωTSωωωTSbω,即 S b S_b Sb与 S ω S_{\omega} Sω的“广义瑞利商”。
ω \omega ω的确定:
分子分母都是关于 ω \omega ω的二次项,因此J与 ω \omega ω的长度无关 J ( ω ) = ( ω ∣ ω ∣ ) T S b ( ω ∣ ω ∣ ) ( ω ∣ ω ∣ ) T S ω ( ω ∣ ω ∣ ) J(\omega)=\frac{\left(\frac{\omega}{|\omega|}\right)^TS_b\left(\frac{\omega}{|\omega|}\right)}{\left(\frac{\omega}{|\omega|}\right)^TS_{\omega}\left(\frac{\omega}{|\omega|}\right)} J(ω)=(∣ω∣ω)TSω(∣ω∣ω)(∣ω∣ω)TSb(∣ω∣ω),只与 ω \omega ω的方向有关。不是一般性,令 ω T S ω ω = 1 \omega^TS_{\omega}\omega=1 ωTSωω=1,则LDA的优化目标等价于 m i n ω − ω T S b ω s . t . ω T S ω ω = 1 \begin{aligned} min_{\omega}\quad -\omega^TS_b\omega\\ s.t.\quad \omega^TS_{\omega}\omega=1 \end{aligned} minω−ωTSbωs.t.ωTSωω=1
相关文章:

西瓜书第三章
广义线性模型 考虑单点可微函数 g ( ⋅ ) g(\cdot) g(⋅),令 y g − 1 ( ω T x b ) yg^{-1}(\omega^{T}xb) yg−1(ωTxb),这样得到的模型称为“广义线性模型”,其中函数 g ( ⋅ ) g(\cdot) g(⋅)称为“联系函数”。显然,对数线…...

关于python如何使用sqlalchemy连接sap_hana数据库
1.先安装sqlalchemy pip install sqlalchemy 2.from sqlalchemy import create_engine 3.创建数据库连接方式: 假设数据连接方式如下: usernameH_TEOPT passwordww122222 jdbcUrljdbc:sap://192.163.1.161:21681/?currentschema 那么使用sqlalchemy 的…...
)
微信小程序教学系列(5)
微信小程序教学系列 第五章:小程序发布与推广 第一节:小程序发布流程介绍 小伙伴们,欢迎来到第五章的教学啦!在这一章中,我们将一起来探索小程序的发布与推广流程。你准备好了吗?让我们开始吧࿰…...

【计算机网络篇】TCP协议
✅作者简介:大家好,我是小杨 📃个人主页:「小杨」的csdn博客 🐳希望大家多多支持🥰一起进步呀! TCP协议 1,TCP 简介 TCP(Transmission Control Protocol)是…...

Disruptor并发编程框架
Disruptor是一款高性能的并发编程框架,主要具有以下特点和功能: 1. RingBuffer环形数据结构 Disruptor的核心数据结构是RingBuffer环形队列,用于存储客户端的并发数据并在生产者和消费者之间传递。队列以批量方式的顺序存储,可以高效地进行并发读写操作。 2. 无锁设计 Disrup…...

matlab 点云精配准(1)——point to point ICP(点到点的ICP)
目录 一、算法原理参考文献二、代码实现三、结果展示四、参考链接本文由CSDN点云侠原创,爬虫自重。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 参考文献 [1] BESL P J,MCKAY N D.A method for registration of 3-Dshapes[J].IEEE Tran…...
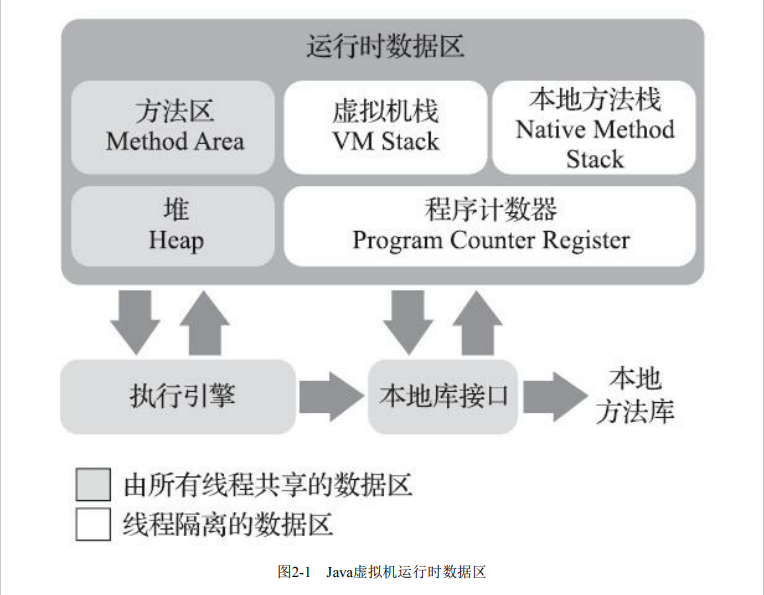
【JVM】运行时数据区域
文章目录 说明程序计数器虚拟机栈本地方法栈Java堆方法区运行时常量池直接内存 说明 Java虚拟机在执行Java程序的过程中会把它所管理的内存划分为若干个不同的数据区域。这些区域有各自的用途,以及创建和销毁的时间,有的区域随着虚拟机进程的启动而一直…...

uniapp踩坑合集
1、onPullDownRefresh下拉刷新不生效 pages.json对应的style中enablePullDownRefresh设置为true,开启下拉刷新 {"path" : "pages/list/list","style" :{"navigationBarTitleText": "页面标题名称","enable…...

再JAVA中如何使用qsort对类进行排序?
目录 结论: 解析: 结论: import java.util.Arrays;class Person implements Comparable<Person>{public String name;public int age;public Person(String name, int age) {this.name name;this.age age;}Overridepublic Stri…...
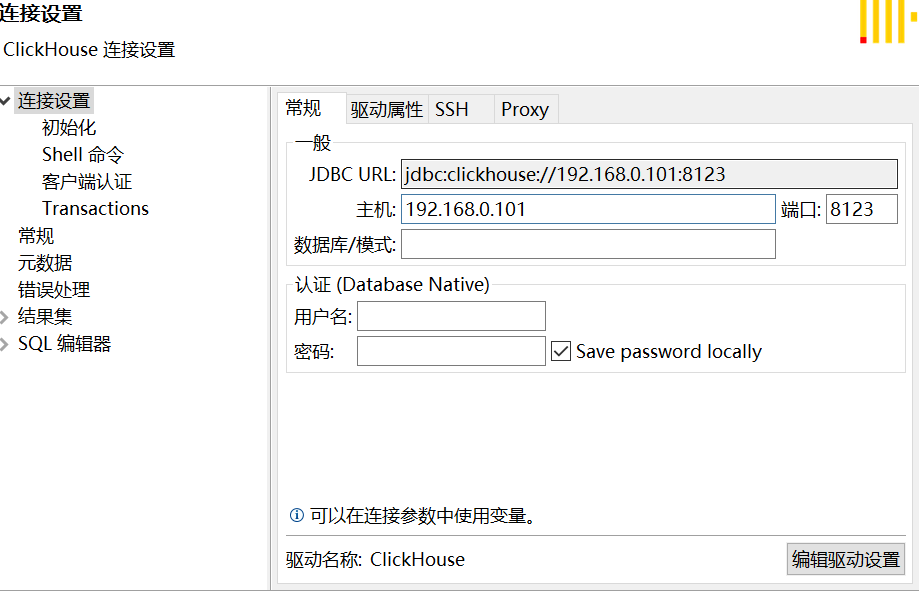
docker安装clickhouse
安装 docker安装 创建clickhouse目录 mkdir -P /data/clickhouse/datamkdir -P /data/clickhouse/confmkdir -P /data/clickhouse/log 拉取镜像 这里直接拉取最新镜像, 如果需要某个特定版本, 则再拉取的时候指定版本号即可. docker pull clickhouse/clickhouse-server 启动临…...
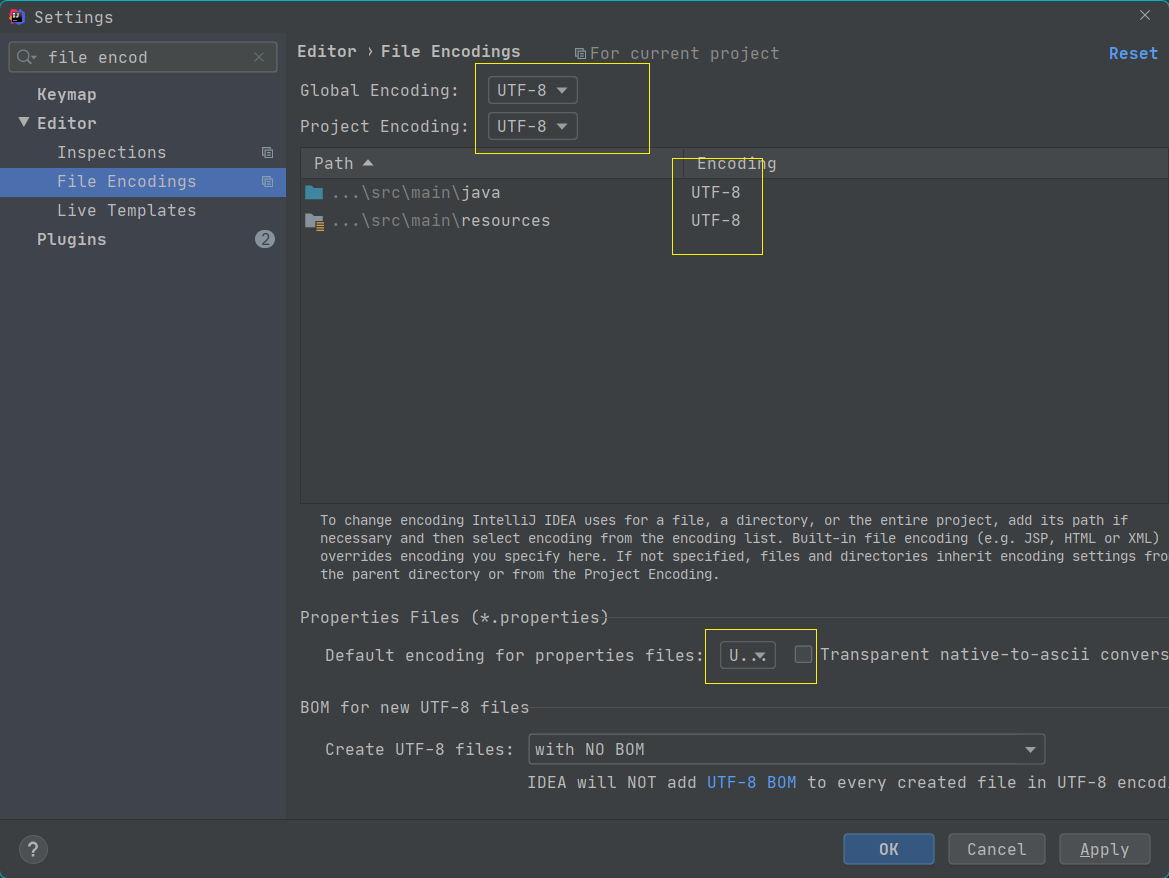
解决`idea`中`database`工具查询起别名乱码问题
文章目录 解决idea中database工具查询起别名乱码问题场景复现如何解决方式一 设置编码方式二:修改字体 原因说明 解决idea中database工具查询起别名乱码问题 场景复现 使用Idea做查询的并且起别名出现了中文乱码 如何解决 方式一 设置编码 settings->输入框输…...
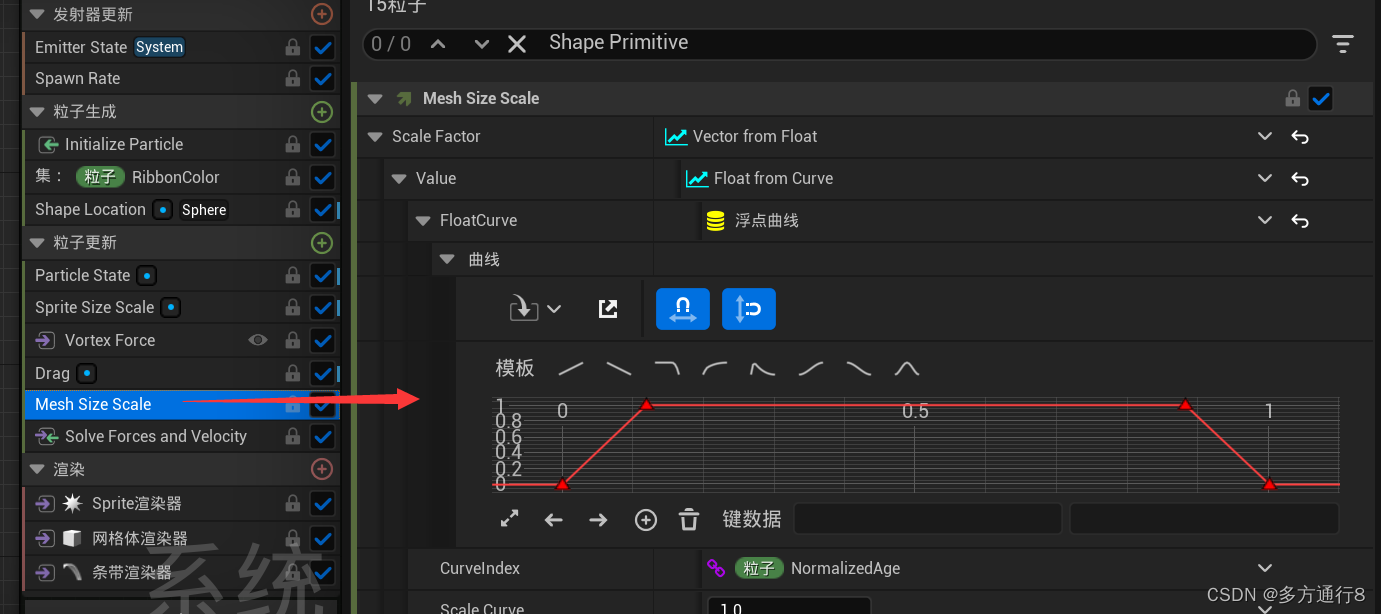
UE4/5Niagara粒子特效之Niagara_Particles官方案例:1.5->2.3
目录 之前的文章: 1.5 Blend Attributes by Value 发射器更新 粒子生成 粒子更新 2.1 Static Beams 编辑 发射器更新: 粒子生成 粒子更新 2.2 Dynamic Beams 没有开始模拟前的效果是: 开始模拟后的效果是: 发射器更新 …...
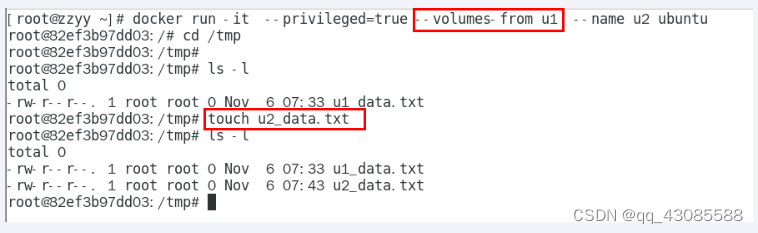
Docker 容器数据卷
Docker挂载主机目录访问如果出现cannot open directory .: Permission denied 解决办法:在挂载目录后多加一个--privilegedtrue参数即可 如果是CentOS7安全模块会比之前系统版本加强,不安全的会先禁止,所以目录挂载的情况被默认为不安全的行…...
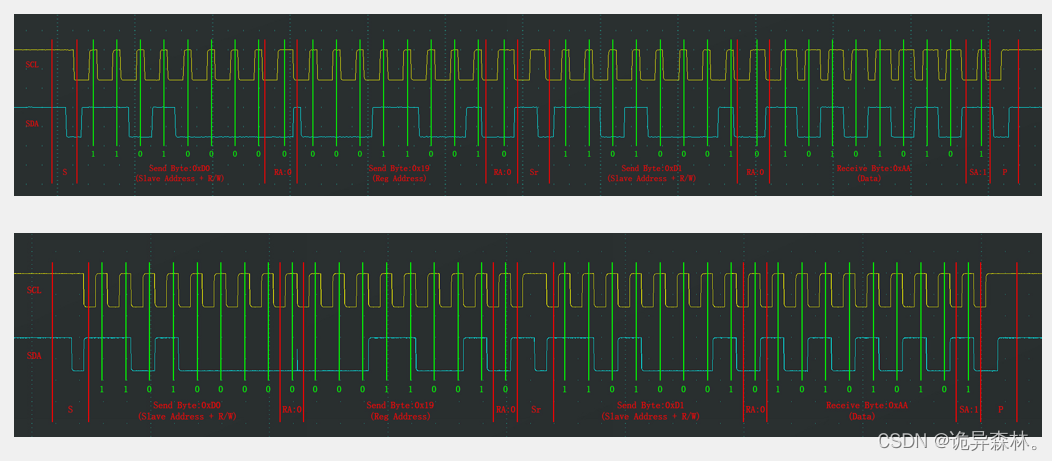
STM32--MPU6050与I2C外设
文章目录 前言MPU6050参数电路MPU6050框图 IIC外设框图 IIC的基本结构软件IIC实现MPU6050硬件IIC实现MPU6050 前言 在51单片机专栏中,用过I2C通信来进行实现AT24C02的数据存储; 里面介绍的是利用程序的编程来实现I2C的时序,进而实现AT24C02与…...

项目管理实战笔记1:项目管理常识
序 看了下极客时间的《项目管理实战》,觉得跟之前学习PMP的标准资料还是有所侧重。重新整理下,相比书上繁杂的知识,这个更通俗易懂。 1 角色转换:三大误区 误区1:事必躬亲 自己做事情是可控的,做项目依赖…...
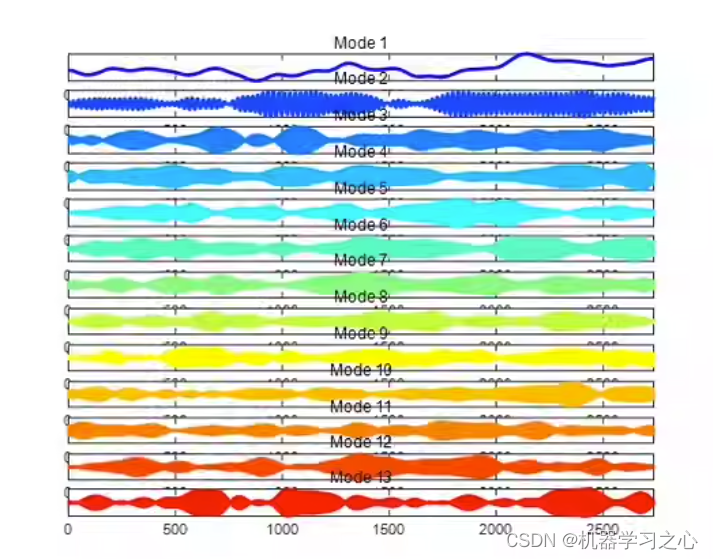
时序分解 | MATLAB实现基于SVMD逐次变分模态分解的信号分解分量可视化
时序分解 | MATLAB实现基于SVMD逐次变分模态分解的信号分解分量可视化 目录 时序分解 | MATLAB实现基于SVMD逐次变分模态分解的信号分解分量可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 SVMD分解算法,分解结果可视化,MATLAB程序ÿ…...

阿里云访问端口被限制解决方法记录
阿里云服务器,80端口可以访问,但是加入了安全组端口8080 通过公网访问改端口策略,发现不能被访问 问题出在防火墙,需要重置一下 解决方法: 在运行的服务器上执行如下命令: # iptables -A INPUT -j ACCEP…...
antd5源码调试环境启动(MacOS)
将源码下载至本地 这里antd5 版本是5.8.3 $ git clone gitgithub.com:ant-design/ant-design.git $ cd ant-design $ npm install $ npm start前提:安装python3、node版本18.14.0(这是本人当前下载的版本) python3安装教程可参考:https://…...

单片机使用基于时间片轮询系统的-状态机-[1]
目的:【1】用C实现一个超轻量化任务管理系统 【2】具有任务suspend, resume, runonce ,auto loop ,task_delay功能 【3】易于移植,不涉及硬件底层。 示例例码: 利用switch case结构实现了单一层的 task_delay功能。弊端就是switch..case不…...

前端开发怎么解决性能优化的问题? - 易智编译EaseEditing
前端性能优化是确保网站或应用在加载速度、响应性和用户体验等方面达到最佳状态的关键任务。以下是一些解决前端性能优化问题的方法: 压缩和合并代码: 压缩和合并CSS、JavaScript和HTML文件可以减少文件大小,加快加载速度。使用压缩工具&am…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
