数据结构——二叉搜索树(附带C++实现版本)
文章目录
- 二叉搜索树
- 概念
- 二叉树的实际应用
- 二叉树模拟实现
- 存储结构
- 二叉搜索树构成
- 二叉搜索树的查找
- 插入操作
- 中序遍历
- 二叉树的删除
- 循环(利用左子树最右节点)
- 递归(利用右子树根节点)
- 二叉树拷贝
- 二叉树资源的销毁
- 二叉树实现完整代码
- 总结
二叉搜索树
概念
二叉搜索树又叫二叉排序树,二叉搜索树也是一种树形结构。
它是一课满足以下性质的搜索树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别是二叉搜索树
注意,二叉搜索树对于值相同的节点只能存储一个
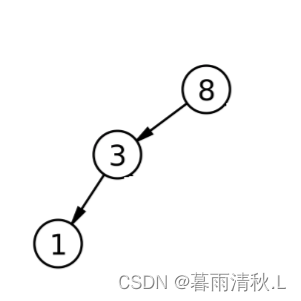
优点:这样的结构能够平均用logn的时间复杂度找到我们想要的值,但是其最坏时间复杂度是O(n), 这是由于搜索二叉树不一定是平衡的,如下图所示:
这个结构也满足二叉搜索树的性质,但是其查找所需要的复杂度是O(n)
二叉树的实际应用
- K模型:K模型只以key为关键码,结构中只需要存储K即可,关键码即为需要搜索道的值。
例如: 给一个单词word,判断该单词是否拼写正确,具体方法如下:
- 以词库中的所有单词集合中的每一个单词作为key,构建一颗二叉搜索树。
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误
- KV模型: 每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方 式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出 现次数就是<word, count>就构成一种键值对
二叉树模拟实现
在这里为大家以kv模型为例模拟实现二叉搜索树,只要稍作修改即可变成k模型。
存储结构
首先,二叉搜索树中存储的是节点,所以我们需要定义一个表示节点的结构体,如下:
template<typename K, typename V>struct BSTree_node{K _key = K();V _value = V();BSTree_node* _left = nullptr;BSTree_node* _right = nullptr;BSTree_node() {}BSTree_node(const K& key, const V& value):_key(key), _value(value){}};
K模型和K,V模型差别就在k,v模型里面还存储了键所对应的值的内容,而k模型没有
二叉搜索树构成
对于二叉搜索树来说,我们想要找到其中的全部成员,和二叉树一样,我们只需要存储它的根节点即可。
template<typename K, typename V>
class BSTree
{//typedef减少代码长度typedef BSTree_node<K, V> node;
private:node* _root = nullptr;
二叉搜索树的查找
由于二叉搜索树的性质,想要从中查找就很简单了。
a. 从根开始比较查找,比根大往右走,比根小往左走。
b. 最多查找高度次,如果走到空还没找到,则这个值不存在
//循环操作
node* find(const K& key)
{//find不需要查找值,只需要查找键node* cur = _root;while (cur){if (cur->_key > key) cur = cur->_left;else if (cur->_key < key) cur = cur->_right;else return cur;}return nullptr;
}
//递归的方式
//由于递归需要传递this指针来找到根节点,而方法不能在外面使用this指针,因此我们需要写一个子函数来完成任务
private:node* _findR(node* root, const K& key){if (!root) return nullptr;if (root->_key < key) return _findR(root->_right, key);else if (root->_key > key) return _findR(root->_left, key);else return root;}
public:node* findR(const K& key){return _findR(_root,key);}
插入操作
插入操作同样两个要点:
a. 如果树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树的位置不断进行比较找到插入位置,如果找到相同值的节点则插入失败,否则插入新节点
同样提供递归和循环两种方法:
//循环
//对于循环,由于当找到空节点的时候并不知道其在其双亲的左侧还是右侧,所以每次变换时需要记录其是在左侧还是右侧//成功插入返回true,插入失败返回falsebool insert(const K& key, const V& value){node* tmp = new node(key, value);if (!_root){_root = tmp;return true;}//需要存储parent,还要存储所在的方向node* parent = nullptr;node* cur = _root;bool is_right = false;while (cur){if (cur->_key < key) {is_right = true;parent = cur;cur = cur->_right;}else if (cur->_key > key) {is_right = false;parent = cur;cur = cur->_left;}else return false;}//出循环时,cur已经指向空指针//如果直接对cur赋值,是在对该拷贝赋值,并没有修改其双亲的指向if (is_right) parent->_right = tmp;else parent->_left = tmp;return true;}//递归//同样,我们需要一个子函数来传递this指针private://这里使用引用是为了解决循环中无法知道新节点在其双亲的左边还是右边的问题bool _insertR(node*& root, const K& key, const V& value)
{//引用解决了找不到父亲的问题if (!root){//由于使用的是引用,这里其实是在修改双亲的指向root = new node(key, value);return true;}if (root->_key < key) return _insertR(root->_right, key, value);else if (root->_key > key) return _insertR(root->_left, key, value);else return false;
}
中序遍历
由于二叉树的特殊性质,其中序遍历一定是有序的,因此我们可以写一个inorder函数输出存储结果用于检验我们操作是否正确实现
private:void _inorder(node* root){if (!root) return;_inorder(root->_left);std::cout << root->_key << ":" << root->_value << std::endl;_inorder(root->_right); }
public:void inorder(){_inorder(_root);std::cout << std::endl;}二叉树的删除
- 首先查找元素是否在二叉树中,如果不存在,则返回
- 如果存在,则删除节点还需要分以下几种情况:
- 要删除的节点无左孩子
- 要删除的节点只有左孩子节点
- 要删除的节点只有右孩子节点
- 要删除的节点有左,右孩子节点
在实际删除过程中,可以将情况1和情况2或情况3合并起来,删除过程如下:
- 情况1: 删除该节点且使被删除节点的双亲节点指向被删除节点的左孩子——直接删除
情况2: 删除该节点且使被删除节点的双亲指向被删除节点的右孩子
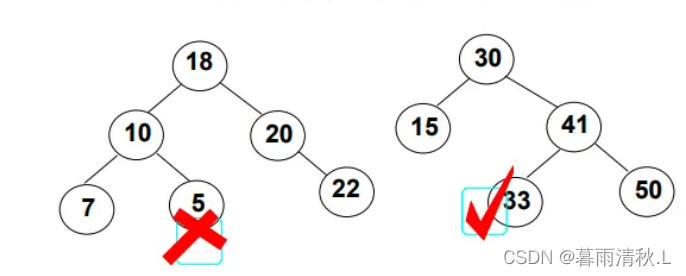
情况3: 寻找和节点的值最相近的节点(左子树最右节点或者该节点右子树的根节点),用它的值填补道被删除节点,然后再来处理该节点的删除问题。
节点的删除操作实现是二叉搜索树中最困难的一个,由于其的细节很多,这里同样还是给出递归和循环各一种方法。
循环(利用左子树最右节点)
对于循环,博主选择了和左子树的最右节点进行交换的方法,这是由于只要找到了左子树的最右节点,和此时的根节点交换,然后就只需要进行左右都没孩子的删除操作即可。
但是,和插入有着同样的问题,我们在查找待删除节点的时候并不知道它在左侧还是右侧,所以我们仍然要保存其双亲节点的位置,但是,还有例外。
先看情况一和情况二:
对于这种情况来说,如果要删除的是根节点,那么其双亲节点的指针就是nullptr,如果不加以判断,就会出错,当待删除节点为根节点时,我们直接将树的_root节点改成_root->left/_root->right即可
情况三:
对于情况三来说,虽然我们需要找的是左子树的最右节点,但是一定不要认为左子树最右节点一定在其双亲的右边,有一种情况是例外的。如下:
如果此时要删除的是根节点,那么其左子树的最右节点就在其双亲的左边,所以我们仍然需要一个标记来判断该节点是在双亲的左边还是右边。
对于二叉树的删除操作来说,循环需要考虑的细节较多,递归虽然也有细节,但是相对更简单一些,但是循环的好处就是不会爆栈,因此在数据量非常大的时候还是使用循环更合适。
循环模拟代码如下:
bool erase(const K& key)
{//可以分为两种大情况//无子节点,有一个子节点 -> 采用托孤处理//托孤要注意删根节点的情况//两个子节点都有 -> 将其与左树最大节点或者右数最小节点相交换,然后删除//第一步先找到要删除的值的位置node* parent = nullptr;node* cur = _root;//保存节点位于其双亲的位置bool is_right = false;while (cur){if (cur->_key < key){is_right = true;parent = cur;cur = cur->_right;}else if (cur->_key > key){is_right = false;parent = cur;cur = cur->_left;}else break;}if (!cur) return false;node* del = cur;//这里需要找到父节点的本质原因是引用不能改变指向if (!cur->_left){//特殊情况,删除的是根节点if (!parent) _root = _root->_right;else{if (is_right) parent->_right = cur->_right;else parent->_left = cur->_right;}}else if (!cur->_right){//同理if (!parent) _root = _root->_left;else{if (is_right) parent->_right = cur->_left;else parent->_left = cur->_left;}}else{//左右两边都不为空//这里循环找左边最大更方便node* leftMax = cur->_left;//bool is_up = true;//出现 特殊情况的本质是下面这个循环没有生效while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;//is_up = false;}std::swap(leftMax->_key, cur->_key);//如果左子树最大节点就是初始的leftMax,则将待删除节点的左指向leftMax的左//if(is_up)if (leftMax == cur->_left) cur->_left = leftMax->_left;else parent->_right = leftMax->_left;//转换待释放的节点del = leftMax;}delete del;return true;
}
递归(利用右子树根节点)
对于递归来说,如果我们选择右子树的根节点进行操作,整个删除过程就可以变成子问题解决。
首先,由于递归可以使用引用作为参数,我们不需要纠结双亲以及其位于双亲左还是右的问题,因此对于循环中情况1,2删除根节点的问题就不需要考虑了
另外,对于情况3来说,选择右子树的根节点也使得情况简单了许多,因为将右子树节点与待删除节点的值交换后,就变成了删除其右子树的根的子问题,完美符合递归的逻辑,直到根只有一个孩子的时侯就变成情况1了,不需要考虑其他特殊情况。
代码如下:
private:bool _erase(node*& root, const K& key)
{if (!root) return false;if (root->_key < key) return _erase(root->_right, key);else if (root->_key > key) return _erase(root->_left, key);else{//用引用就不需要考虑父亲指向的问题了if (!root->_left) {root = root->_right;return true;}else if (!root->_right){root = root->_left;return true;}else{swap(root->_key, root->_right->_key);return _erase(root->_right, key);}}
}
public:bool eraseR(const K& key){_erase(_root, key);}
二叉树拷贝
二叉树的拷贝构造也可以利用递归的性质来实现,先拷贝根节点,然后拷贝左子树,最后拷贝右子树,拷贝左子树和右子树的逻辑与主逻辑相同。
代码:
private:node* _copy(node*& root, node* copy){if (!copy) return nullptr;root = new node(copy->_key, copy->_value);root->_left = _copy(root->_left, copy->_left);root->_right = _copy(root->_right, copy->_right);return root;}
public:BSTree(const BSTree& t){_copy(_root, t._root);}
二叉树资源的销毁
由于二叉树的节点都是new出来的节点,所以我们在结束使用时也需要释放资源,否则就会导致内存泄漏的问题,对于释放资源,我们可以放在析构函数解决,运用递归后序遍历的思路,先释放左子树的资源,然后释放右子树的资源,最后释放根节点的资源,代码如下:
private:void _destroy(node* root){if (!root) return;_destroy(root->_left);_destroy(root->_right);delete root;}public:~BSTree(){_destroy(_root);}
二叉树实现完整代码
#pragma once
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;namespace key_value
{template<typename K, typename V>struct BSTree_node{K _key = K();V _value = V();BSTree_node* _left = nullptr;BSTree_node* _right = nullptr;BSTree_node() {}BSTree_node(const K& key, const V& value):_key(key), _value(value){}};template<typename K, typename V>class BSTree{typedef BSTree_node<K, V> node;private:node* _root = nullptr;void _inorder(node* root){if (!root) return;_inorder(root->_left);std::cout << root->_key << ":" << root->_value << std::endl;_inorder(root->_right); }bool _insertR(node*& root, const K& key, const V& value){//引用解决了找不到父亲的问题if (!root){root = new node(key, value);return true;}if (root->_key < key) return _insertR(root->_right, key, value);else if (root->_key > key) return _insertR(root->_left, key, value);else return false;}node* _findR(node* root, const K& key){if (!root) return nullptr;if (root->_key < key) return _findR(root->_right, key);else if (root->_key > key) return _findR(root->_left, key);else return root;}//同理,这里要修改的不是局部变量,而是上一个指针的指向,所以要使用引用bool _erase(node*& root, const K& key){if (!root) return false;if (root->_key < key) return _erase(root->_right, key);else if (root->_key > key) return _erase(root->_left, key);else{//用引用就不需要考虑父亲指向的问题了if (!root->_left) {root = root->_right;return true;}else if (!root->_right){root = root->_left;return true;}else{swap(root->_key, root->_right->_key);return _erase(root->_right, key);}}}void _destroy(node* root){if (!root) return;_destroy(root->_left);_destroy(root->_right);delete root;}node* _copy(node*& root, node* copy){if (!copy) return nullptr;root = new node(copy->_key, copy->_value);root->_left = _copy(root->_left, copy->_left);root->_right = _copy(root->_right, copy->_right);return root;}public:BSTree() {}//循环///插入,如果已经存在就不用插入bool insert(const K& key, const V& value){node* tmp = new node(key, value);if (!_root){_root = tmp;return true;}//需要存储parent,还要存储所在的方向node* parent = nullptr;node* cur = _root;bool is_right = false;while (cur){if (cur->_key < key) {is_right = true;parent = cur;cur = cur->_right;}else if (cur->_key > key) {is_right = false;parent = cur;cur = cur->_left;}else return false;}//出循环时,cur已经指向空指针if (is_right) parent->_right = tmp;else parent->_left = tmp;return true;}node* find(const K& key){//find不需要查找值,只需要查找键node* cur = _root;while (cur){if (cur->_key > key) cur = cur->_left;else if (cur->_key < key) cur = cur->_right;else return cur;}return nullptr;}bool erase(const K& key){//可以分为两种大情况//无子节点,有一个子节点 -> 采用托孤处理//托孤要注意删根节点的情况//两个子节点都有 -> 将其与左树最大节点或者右数最小节点相交换,然后删除//第一步先找到要删除的值的位置node* parent = nullptr;node* cur = _root;//保存节点位于其双亲的位置bool is_right = false;while (cur){if (cur->_key < key){is_right = true;parent = cur;cur = cur->_right;}else if (cur->_key > key){is_right = false;parent = cur;cur = cur->_left;}else break;}if (!cur) return false;node* del = cur;//这里需要找到父节点的本质原因是引用不能改变指向if (!cur->_left){//特殊情况,删除的是根节点if (!parent) _root = _root->_right;else{if (is_right) parent->_right = cur->_right;else parent->_left = cur->_right;}}else if (!cur->_right){//同理if (!parent) _root = _root->_left;else{if (is_right) parent->_right = cur->_left;else parent->_left = cur->_left;}}else{//左右两边都不为空//这里循环找左边最大更方便node* leftMax = cur->_left;//bool is_up = true;//出现 特殊情况的本质是下面这个循环没有生效while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;//is_up = false;}std::swap(leftMax->_key, cur->_key);//如果左子树最大节点就是初始的leftMax,则将待删除节点的左指向leftMax的左//if(is_up)if (leftMax == cur->_left) cur->_left = leftMax->_left;else parent->_right = leftMax->_left;//转换待释放的节点del = leftMax;}delete del;return true;}//递归///中序遍历void inorder(){_inorder(_root);std::cout << std::endl;}bool insertR(const K& key, const V& value){return _insertR(_root, key, value);}node* findR(const K& key) { return _findR(_root, key); }bool eraseR(const K& key){_erase(_root, key);}~BSTree(){_destroy(_root);}BSTree(const BSTree& t){_copy(_root,t._root);}};//测试用例1void test_BSTree(){int a[] = { 8,3,1,10,6,4,7,14,13 };BSTree<int, int> bst;for (auto e : a) bst.insert(e,e);std::cout << bst.find(8)->_key << std::endl;std::cout << bst.find(13)->_key << std::endl;//std::cout << bst.find(18)->_key << std::endl;BSTree<int, int> t1(bst);t1.inorder();bst.erase(4);bst.inorder();bst.erase(6);bst.inorder();bst.erase(7);bst.inorder();bst.erase(3);bst.inorder();for (auto e : a){bst.erase(e);}bst.inorder();}//测试用例2void TestBSTree(){BSTree<string, string> dict;dict.insertR("insert", "插入");dict.insertR("erase", "删除");dict.insertR("left", "左边");dict.insertR("string", "字符串");string str;while (cin >> str){auto ret = dict.findR(str);if (ret){cout << str << ":" << ret->_value << endl;}else{cout << "单词拼写错误" << endl;}}string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };// 统计水果出现的次BSTree<string, int> countTree;for (auto str : strs){auto ret = countTree.findR(str);if (ret == nullptr){countTree.insertR(str, 1);}else{ret->_value++;}}BSTree<string, int> t1(countTree);countTree.inorder();t1.inorder();}
}
总结
前面提到了对于二叉查找树来说,
- 最好情况下二叉树为完全二叉树(或接近完全二叉树),其平均比较次数为: l o g 2 N log_2 N log2N
- 但最坏情况下,二叉搜索树有可能退化成单支树(或类似单支),其平均比较次数为: N 2 \frac{N}{2} 2N
那么就有一个问题了,如果退化成单支树,二叉搜索树的性能就消失了,那么是否能够改进,不论按什么次数插入关键码,二叉搜索树的性能都能达到最优呢?
那么就需要用到AVL树和红黑树了,这两种树都是特殊的搜索二叉树,但是底层相对于普通的二叉搜索树又复杂了许多,加入了翻转二叉树等操作来达到最有优效率!
STL中的map和set底层就是用红黑树实现的,其做到了查找最坏时间复杂度为 O ( l o g 2 N ) O(log_2 N) O(log2N),这样大家就感受到红黑树的强大了把!
对于AVL树和红黑树的知识,博主会在之后的博客中讲解,大家敬请期待!
以上就是二叉树实现的增删查改的相关知识内容,完整代码以及其作用和性能分析的总结了,希望大家看完能够有所收获!如果对博主的内容有疑惑或者博主内容有误的话,欢迎评论区指出!
相关文章:
数据结构——二叉搜索树(附带C++实现版本)
文章目录 二叉搜索树概念 二叉树的实际应用二叉树模拟实现存储结构二叉搜索树构成二叉搜索树的查找插入操作中序遍历二叉树的删除循环(利用左子树最右节点)递归(利用右子树根节点) 二叉树拷贝二叉树资源的销毁 二叉树实现完整代码总结 二叉搜索树 概念 二叉搜索树…...
C++对C的扩展Extension)
C++(3)C++对C的扩展Extension
类型增强 1、类型更加严格 不初始化,无法通过编译;C不初始化,则随机赋值 #include <iostream> #include <stdlib.h>int main() {const int a 100; //真正的const,无法修改 // int *p &a; 报错const int *p…...
使用GitHub账号、Copilot异常)
在vscode(idea)使用GitHub账号、Copilot异常
在idea使用GitHub账号、Copilot异常 登录GitHub显示 Invalid authentication data.Connection refused: connect或者副驾驶显示 Failed to initiate the GitHub login process. Please try again.一般网上的方法推荐使用token登录,或者降级副驾驶 经过研究&#x…...

新的后端渲染:服务器驱动UI
通过API发送UI是一种彻底的新方法,将改变传统的UI开发。 一项正在改变我们对用户界面 (UI) 的看法的技术是通过 API 发送 UI,也称为服务器驱动UI。这种方法提供了新水平的活力和灵活性,正在改变 UI 开发的传统范例。 服务器驱动 UI 不仅仅是…...

Postman如何做接口自动化测试?
前言 什么是自动化测试 把人对软件的测试行为转化为由机器执行测试行为的一种实践。 例如GUI自动化测试,模拟人去操作软件界面,把人从简单重复的劳动中解放出来。 本质是用代码去测试另一段代码,属于一种软件开发工作,已经开发完…...

excel文本函数篇2
本期主要介绍LEN、FIND、SEARCH以及后面加B的情况: (1)后缀没有B:一个字节代表一个中文字符 (2)后缀有B:两个字节代表一个中文字符 1、LEN(text):返回文本字符串中的字符个数 2、…...
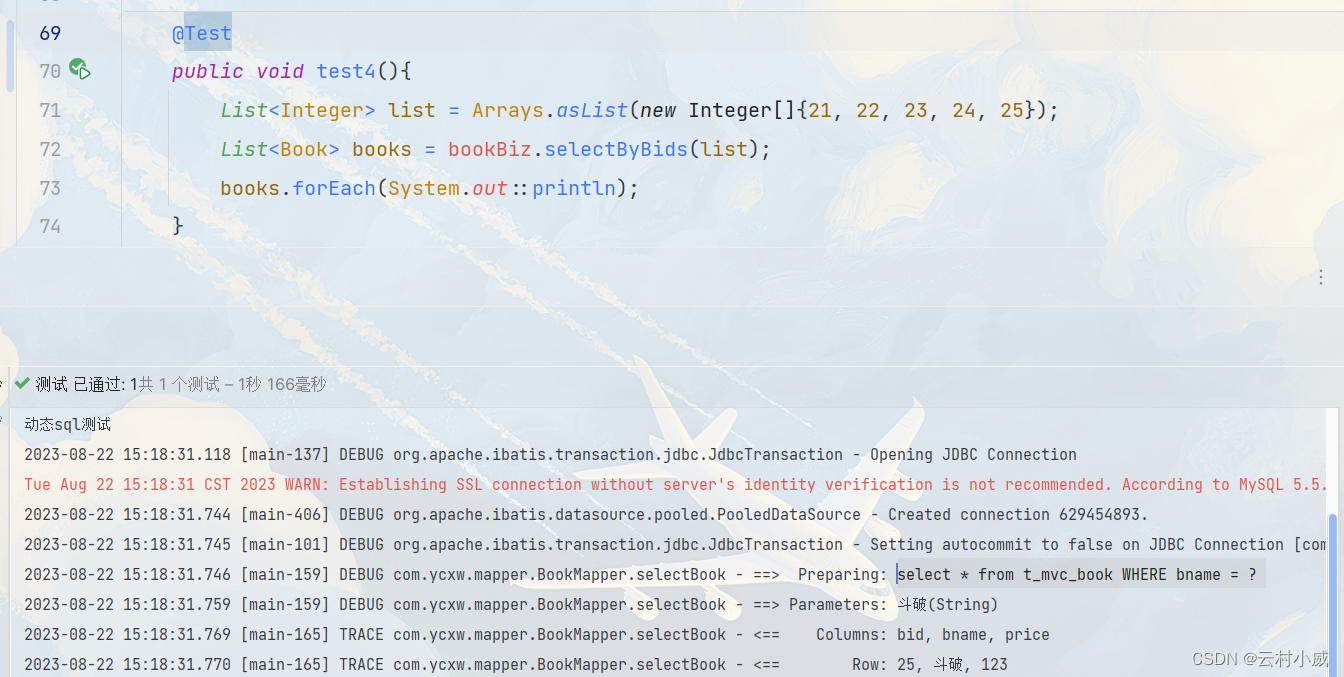
【MyBatis】动态SQL > 重点:${...}和#{...}与resultMap和resultType的区别
目录 一、MyBatis动态sql 1.1 动态sql的作用 1.2 动态sql作用论证 1.2.1 条件判断:<if> 1.2.2 循环迭代:<foreach> 1.2.3 SQL片段重用 1.2.4 动态条件组合:<choose><when><otherwise> 1.2.5 <where…...

什么是BEM命名规范?为什么要使用BEM命名规范?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ BEM命名规范⭐ 为什么使用BEM命名规范?⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为…...

JavaScript:交集和差集的应用场景
在集合A和集合B中,属于集合A,同时也属于集合B的元素组成的集合,就是交集。 在A中所有不属于集合B元素,组合成集合,就是差集。 那么在平时的开发中,如何使用差集和交集来解决问题呢? 现在有这…...
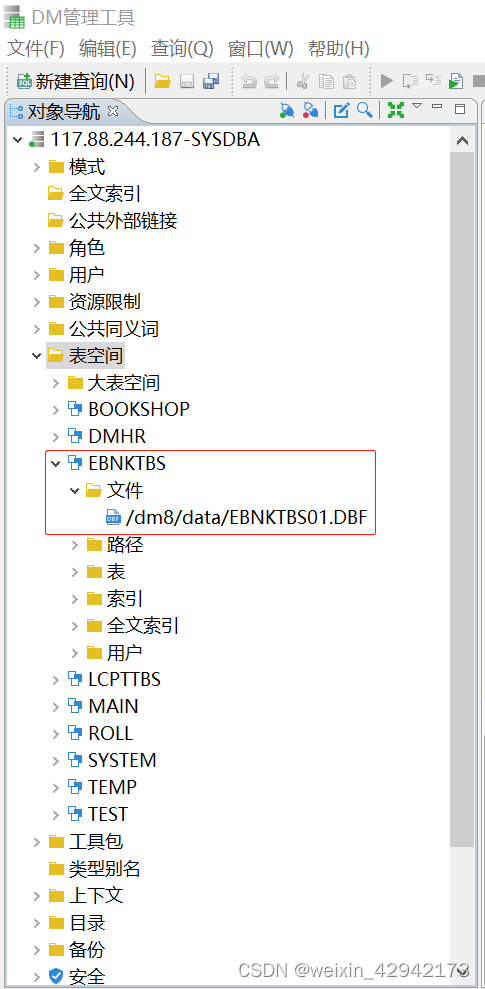
达梦数据库表空间创建和管理
概述 本文将介绍在达梦数据库如何创建和管理表空间。 1.创建表空间 1.1表空间个数限制 理论上最多允许有65535个表空间,但用户允许创建的表空间 ID 取值范围为0~32767, 超过 32767 的只允许系统使用,ID 由系统自动分配,ID不能…...

三、MySQL 数据库安装集
一、CentOS—YUM 1. MySQL—卸载 # 1、查看存在的MySQL。 rpm -qa | grep -i mysql rpm -qa | grep mysql# 2、删除存在的MySQL。 rpm -e –-nodeps 包名# 3、查找存在的MySQL目录。 find / -name mysql# 4、删除存在的MySQL目录。 rm -rf 目录# 5、删除存在的MySQL配置文件。…...
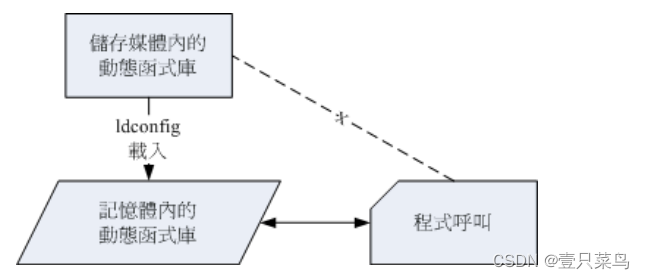
【BASH】回顾与知识点梳理(三十九)
【BASH】回顾与知识点梳理 三十九 三十九. make、tarball、函数库及软件校验39.1 用 make 进行宏编译为什么要用 makemakefile 的基本语法与变量 39.2 Tarball 的管理与建议使用原始码管理软件所需要的基础软件Tarball 安装的基本步骤一般 Tarball 软件安装的建议事项 (如何移除…...

蓝蓝设计-UI设计公司案例-HMI列车监控系统界面设计解决方案
2013年,为加拿大庞巴迪(Bombardier)设计列车监控系统界面设计。 2015-至今,为中车集团旗下若干公司提供HMI列车监控系统界面设计,综合考虑中车特点、城轨车、动车组的不同需求以及HMI硬键屏和触摸 屏的不同操作方式,重构框架设计、交互设计、…...

Blazor前后端框架Known-V1.2.13
V1.2.13 Known是基于C#和Blazor开发的前后端分离快速开发框架,开箱即用,跨平台,一处代码,多处运行。 Gitee: https://gitee.com/known/KnownGithub:https://github.com/known/Known 概述 基于C#和Blazo…...

vue 复制文本
一个常用的库就是 clipboard.js,它可以帮助您实现跨浏览器的复制到剪贴板功能 首先,安装 clipboard.js: cnpm install clipboard 创建一个 Vue 组件并使用 clipboard.js: <template><div><input v-model"…...
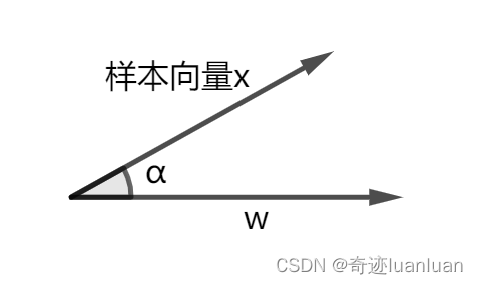
西瓜书第三章
广义线性模型 考虑单点可微函数 g ( ⋅ ) g(\cdot) g(⋅),令 y g − 1 ( ω T x b ) yg^{-1}(\omega^{T}xb) yg−1(ωTxb),这样得到的模型称为“广义线性模型”,其中函数 g ( ⋅ ) g(\cdot) g(⋅)称为“联系函数”。显然,对数线…...

关于python如何使用sqlalchemy连接sap_hana数据库
1.先安装sqlalchemy pip install sqlalchemy 2.from sqlalchemy import create_engine 3.创建数据库连接方式: 假设数据连接方式如下: usernameH_TEOPT passwordww122222 jdbcUrljdbc:sap://192.163.1.161:21681/?currentschema 那么使用sqlalchemy 的…...
)
微信小程序教学系列(5)
微信小程序教学系列 第五章:小程序发布与推广 第一节:小程序发布流程介绍 小伙伴们,欢迎来到第五章的教学啦!在这一章中,我们将一起来探索小程序的发布与推广流程。你准备好了吗?让我们开始吧࿰…...

【计算机网络篇】TCP协议
✅作者简介:大家好,我是小杨 📃个人主页:「小杨」的csdn博客 🐳希望大家多多支持🥰一起进步呀! TCP协议 1,TCP 简介 TCP(Transmission Control Protocol)是…...

Disruptor并发编程框架
Disruptor是一款高性能的并发编程框架,主要具有以下特点和功能: 1. RingBuffer环形数据结构 Disruptor的核心数据结构是RingBuffer环形队列,用于存储客户端的并发数据并在生产者和消费者之间传递。队列以批量方式的顺序存储,可以高效地进行并发读写操作。 2. 无锁设计 Disrup…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...