算法通关村第九关——中序遍历与搜索树
1 中序遍历和搜索树原理
二叉搜索树按照中序遍历正好是一个递增序列。其比较规范的定义是:
- 若它的左子树不为空,则左子树上所有节点的值均小于它的根节点的值;
- 若它的右子树不为空,则右子树所有节点的值均大于它的根节点的值;
- 它的左、右子树也分别为二叉搜索树,比如下面的例子:

这两棵树的中序遍历分别是[1, 2, 3, 4, 5, 6, 7, 8, 9]和[6, 7, 8, 9],都是二叉搜索树。
2 二叉搜索树中搜索特定值
力扣700题,给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
比如target为3,给定二叉搜索树:
5/ \3 4/ \1 2
应该返回如下子树:
3 / \1 2
2.1 递归实现
使用递归来实现,先来分析一下有哪些情况:
- 如果根节点
root === null或者root.val === target就直接返回根节点; - 如果
target < root.val,说明比右子树的值小,去根节点的左子树进行查找searchBST(root.left, target); - 如果
target > root.val,说明比左子树的值大,去根节点的右子树进行查找searchBST(root.right, target)。
递归完整代码如下:
// 递归法
function searchBST(root, target) {// 如果根节点为空或者root.val === target,直接返回rootif (root === null || root.val === target) {return root;}// 如果target < root.val,进入根节点的左子树查找// 如果target > root.val,进入根节点的右子树查找return target < root.val ? searchBST(root.left, target) : searchBST(root.right, target);
}
2.2 迭代实现
迭代逻辑:
- 如果根节点
root === null或者root.val !== target,进入下面的判断- 如果
target < root.val,说明比右子树的值小,去根节点的左子树进行查找,root = root.left; - 如果
target > root.val,说明比左子树的值大,去根节点的右子树进行查找,root = root.right
- 如果
迭代完整代码如下:
// 迭代法
function searchBST(root, target) {// 如果根节点为空或者target !== root.valwhile (root !==null && target !== root.val) {// 如果target < root.val,进入根节点的左子树查找,root = root.left// 如果target > root.val,进入根节点的右子树查找,root = root.rightroot = (target < root.val ? root.left : root.right);}return root;
}3 验证二叉搜索树
力扣98题,给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。有效二叉树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
分析:根据题目以及中序遍历的特性,可以知道二叉搜索树中序遍历得到的序列是一个升序序列,要判断是否是一个有效二叉树,只需要在中序遍历的时候一边遍历一边检查当前节点的值是否大于前一个遍历到的节点值即可。
3.1 递归实现
递归实现,代码如下:
function isValidBST(root) {let pre = Number.MIN_SAFE_INTEGER;return validBST(root);function validBST(node) {if (node === null) {return true;}// 如果左子树某个元素不满足要求就退出if (!validBST(node.left)) {return false;}// 如果当前节点值≤中序遍历前一个节点的值,不能满足二叉搜索树条件if (node.val <= pre) {return false;}pre = node.val;return validBST(node.right);}
}
3.2 迭代实现
测试用例的最小节点有可能是javascript中的最小值,因此初始化preVal = -Infinity。
function isValidBST(root) {const nodeStack= [];let preVal = -Infinity;while (nodeStack.length !== 0 || root !== null) {while (root !== null) {nodeStack.push(root);// 先遍历左子树root = root.left;}// 比较左子树中间根节点与前一个节点的值,如果小与前一个节点值,说明不是二叉搜索树root = nodeStack.pop();if (root.val <= preVal) {return false;}preVal = root.val;// 再遍历右子树root = root.right;}return true;
}
相关文章:

算法通关村第九关——中序遍历与搜索树
1 中序遍历和搜索树原理 二叉搜索树按照中序遍历正好是一个递增序列。其比较规范的定义是: 若它的左子树不为空,则左子树上所有节点的值均小于它的根节点的值;若它的右子树不为空,则右子树所有节点的值均大于它的根节点的值&…...
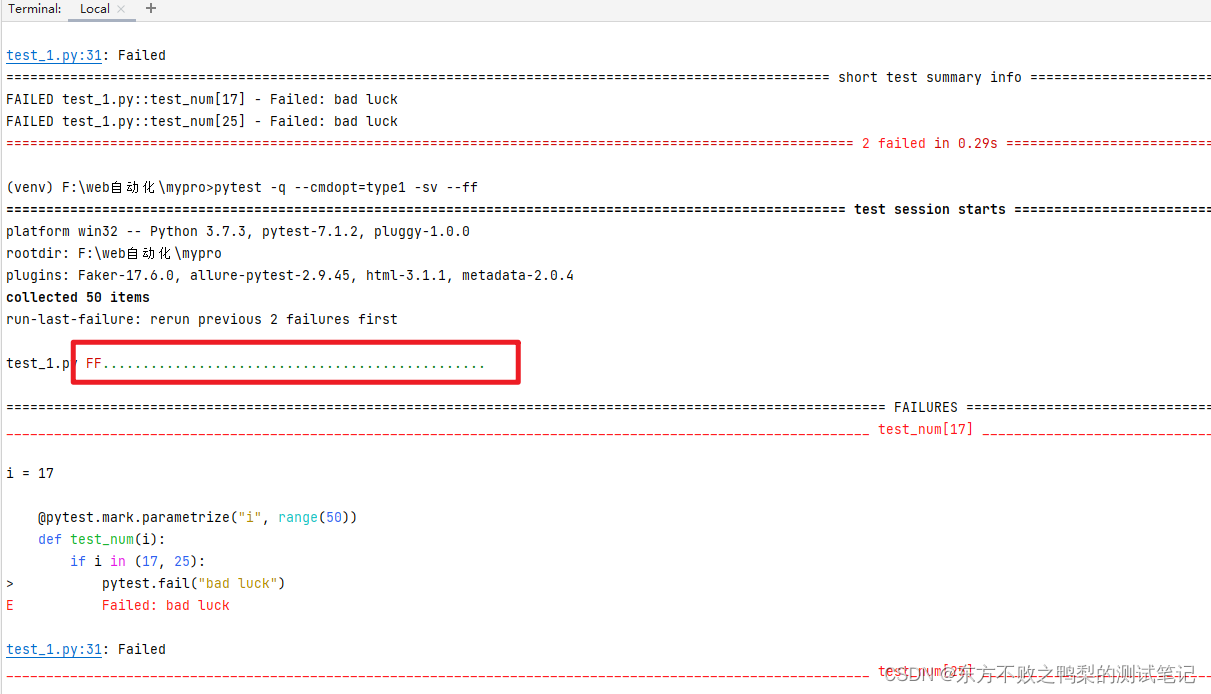
测试框架pytest教程(5)运行失败用例-rerun failed tests
# content of test_50.py import pytestpytest.mark.parametrize("i", range(50)) def test_num(i):if i in (17, 25):pytest.fail("bad luck") 运行这个文件,2个失败,48个通过。 要运行上次失败的测试用例,可以使用--l…...
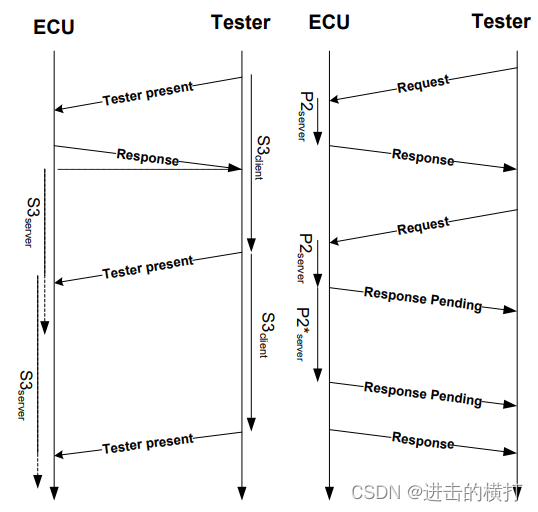
【车载开发系列】UDS当中的时间参数
【车载开发系列】UDS当中的时间参数 UDS当中的时间参数 【车载开发系列】UDS当中的时间参数一. 术语定义二. 网络层时间调整参数三. ECU诊断层与会话层参数 一. 术语定义 缩写全称中文说明BSBlock Size块大小STminSeparation time min时间间隙SIService Identifier服务标识符S…...

PDF中的表格怎么转换为Excel?这两个工具一定得收藏!
PDF是一种常见的文件格式,它可以保持文件的原始样式和内容,但是也有一些缺点,比如不易编辑和处理数据。如果你想要将PDF中的表格或数据导出到Excel中,以便进行分析、计算或制作图表,那么你可能需要一个专业的PDF转Exce…...

ssh scp sshpass
ssh命令用于远程连接主机 ssh usernamehostname更多用法参考: ssh常用用法 scp 命令是用于通过 SSH 协议安全地将文件复制到远程系统和从远程系统复制文件到本地的命令 比如: scp /data/log/a.txt root192.168.1.100:/data/log该命令就就将本地的a.t…...
)
leetcode 1996. 游戏中弱角色的数量(排序的魅力)
题目 题意: 给定n个人的攻击力和防御力,对于一个人来说,如果存在某个人的攻击力和防御力都比他高,那么称这个人为弱角色。统计弱角色的数量 思路: 排序,攻击力按从大到小排序,这样遍历的时候某个数时前边的攻击力都比他…...
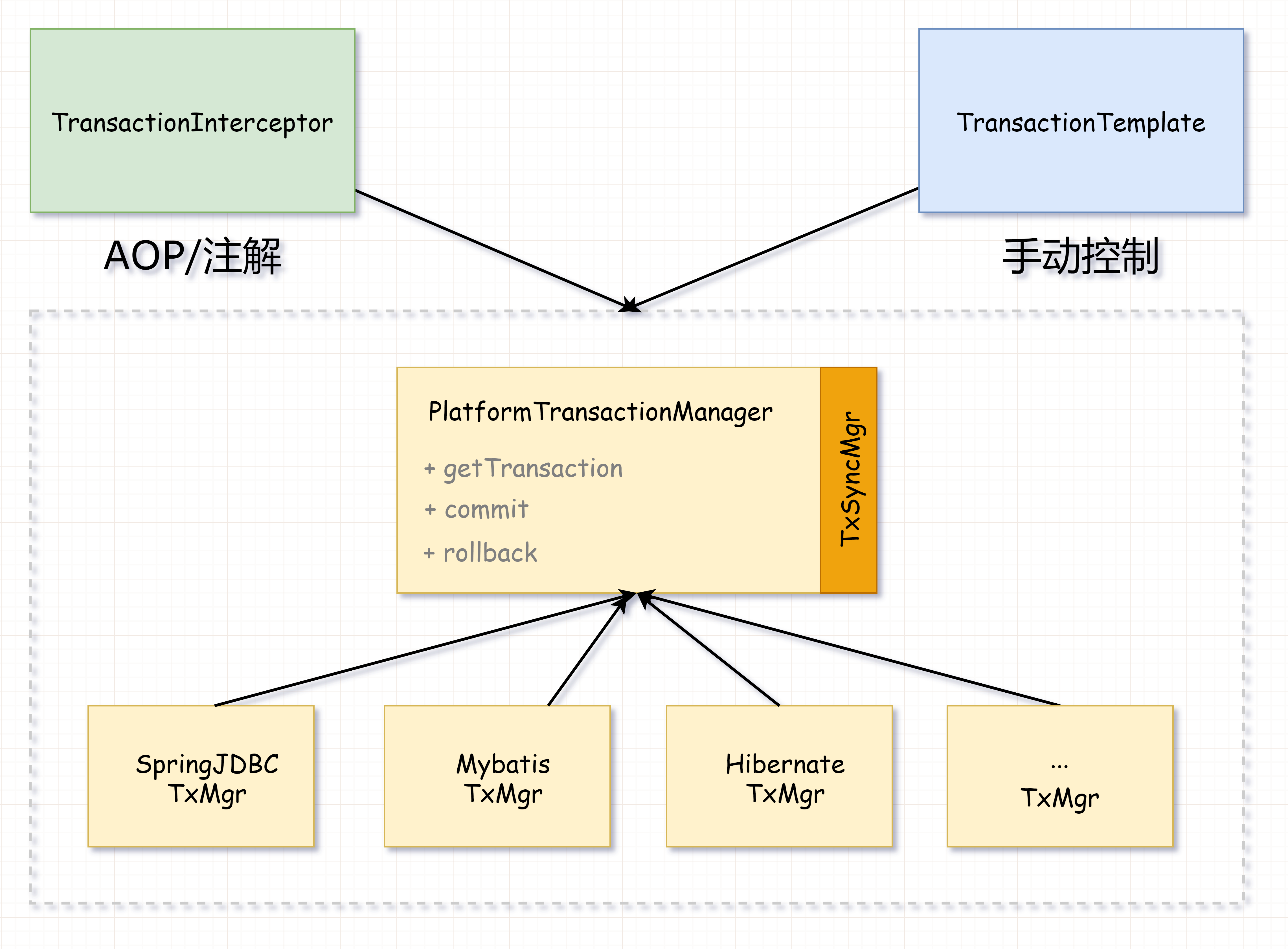
从头到尾说一次 Spring 事务管理(器) | 京东云技术团队
事务管理,一个被说烂的也被看烂的话题,还是八股文中的基础股之一。 本文会从设计角度,一步步的剖析 Spring 事务管理的设计思路(都会设计事务管理器了,还能玩不转?) 为什么需要事务管理&…...
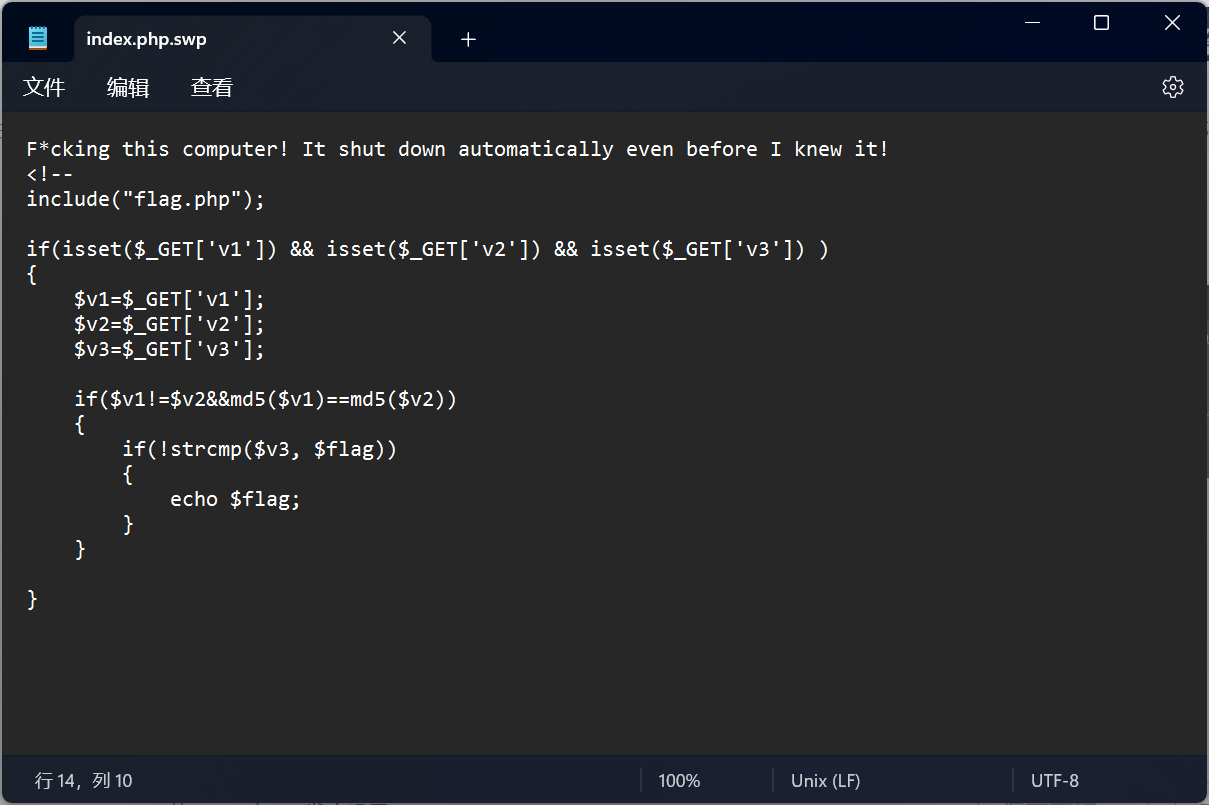
php 系列题目,包含查看后端源代码
一、弱类型比较问题 原则: 1.字符串和数字比较,字符串回被转换成数字。 "admin" 0(true) admin被转换成数字,由于admin是字符串,转换失败,变成0 int(admin)0,所以比较结果是ture 2.混合字符串转…...

令牌桶C语言代码实现
令牌桶实例 令牌桶三要素 cps 每秒钟传输字节数 burst 令牌桶内最多能传输的字节数,token的最大值 token 令牌的个数 之前是一个令牌(token)对应一个字节,现在将一个token变为一个cps,cps是解码速率,每攒到一个令牌ÿ…...
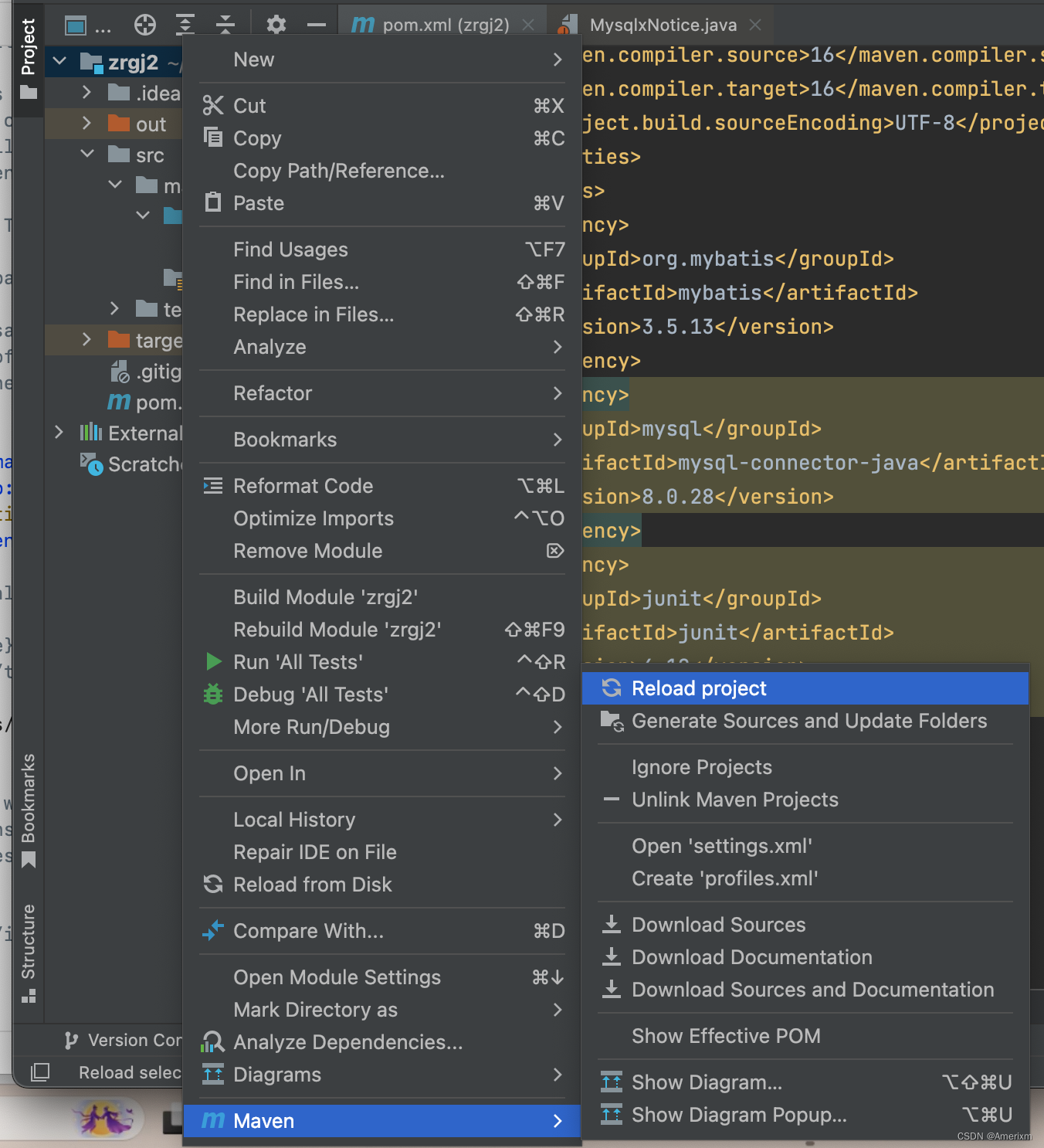
Mybatis 建立依赖失败:报错Dependency ‘mysql:mysql-connector-java:8.0.28‘ not found
Mybatis 建立依赖失败:报错Dependency ‘mysql:mysql-connector-java:8.0.28’ not found 解决办法: 写完依赖代码,直接重构,下载依赖。 图片: 
多线程+隧道代理:提升爬虫速度
在进行大规模数据爬取时,爬虫速度往往是一个关键问题。本文将介绍一个提升爬虫速度的秘密武器:多线程隧道代理。通过合理地利用多线程技术和使用隧道代理,我们可以显著提高爬虫的效率和稳定性。本文将为你提供详细的解决方案和实际操作价值&a…...

使用@Configuration和@Bean给spring容器中注入组件
Confguration->告诉spring这是一个配置类 以前我们是使用配置文件来注册bean的,现如今可以用Configuration 来代替配置文件。 //配置配配置文件 Configuration // 告诉Spring这是一个配置类,等同于以前的配置文件 public class MainConfig {// Bean注解是给IOC…...
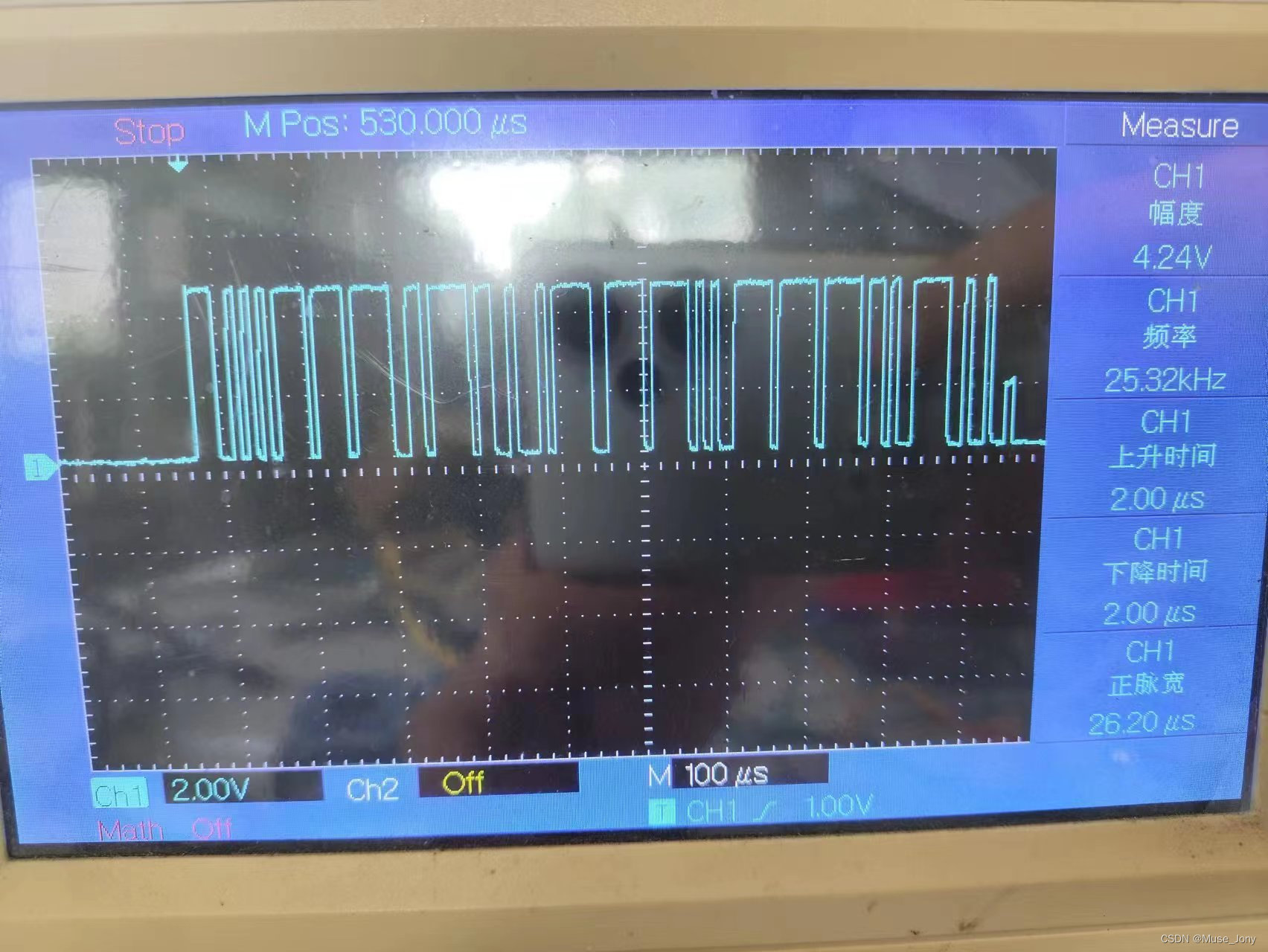
信号波形解读
can波形解读 实际波形 标准帧 发送数据 仲裁段 0x1AA 数据长度为8字节 内容为:0x41, 0x20, 0x38, 0x41, 0x00, 0x16, 0x00, 0x00 波特率 111K...
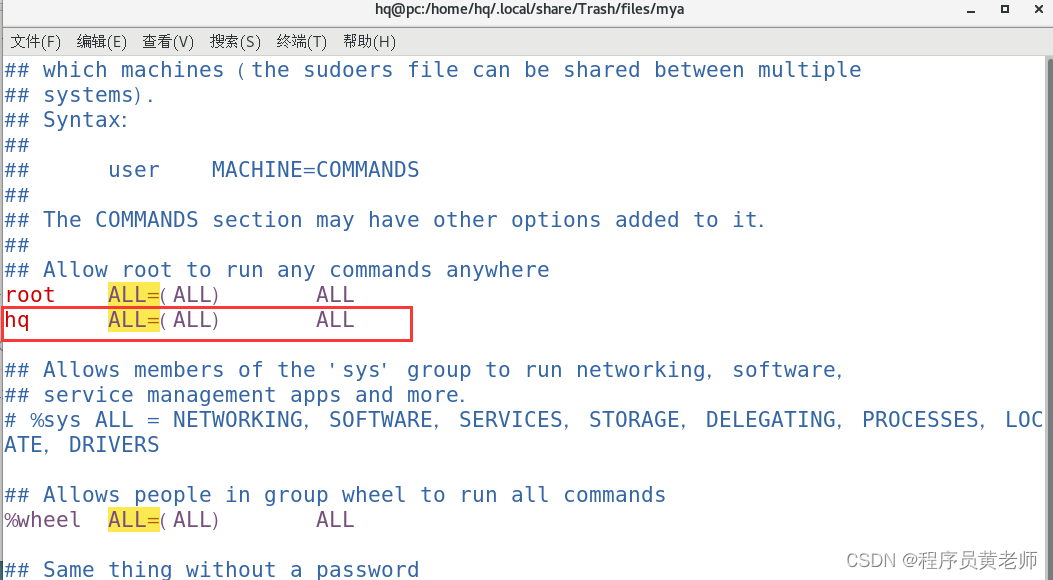
Centos 解决 XXX不在 sudoers 文件中。此事将被报告。的错误
本来想使用 sudo 拷贝一个文件,结果出现上面的问题! 下面是解决方法: 首先登录root,然后执行下面的命令 vim /etc/sudoers 将你需要添加的用户带红色框线的地方,模仿root写一遍,然后保存! …...

雪花算法和uuid的区别
雪花算法(Snowflake Algorithm)和 UUID(Universally Unique Identifier)都是用于生成唯一标识符的方法,但它们在实现和适用场景上存在一些区别。 雪花算法: 雪花算法是Twitter开发的一种分布式ID生成算法…...
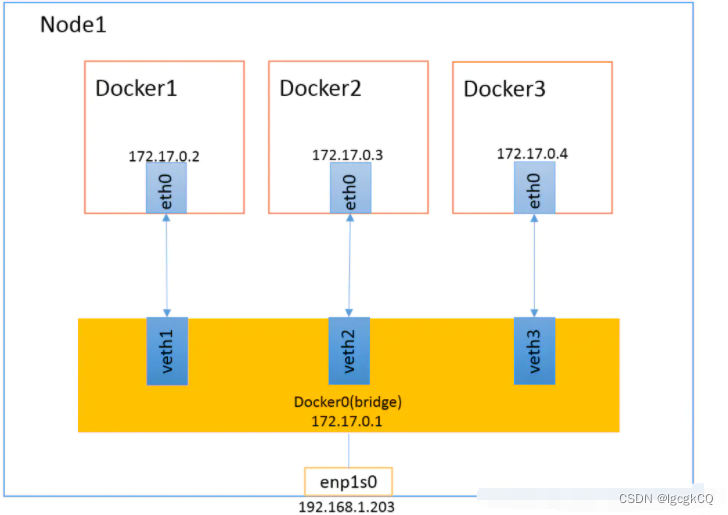
docker之DockerFile与网络
目录 DockerFile 构建步骤 基础知识 指令 实战:构建自己的centos 第一步:编写dockerfile文件 第二步:构建镜像文件 docker网络 原理 功能 网络模式 host模式 container模式 none模式 bridge模式 DockerFile dockerfile 是用来…...

知识蒸馏开山之作(部分解读)—Distilling the Knowledge in a Neural Network
1、蒸馏温度T 正常的模型学习到的就是在正确的类别上得到最大的概率,但是不正确的分类上也会得到一些概率尽管有时这些概率很小,但是在这些不正确的分类中,有一些分类的可能性仍然是其他类别的很多倍。但是对这些非正确类别的预测概率也能反…...

centos 7 安装 docker-compose curl 设置代理
sudo curl -x “http://192.168.1.2:3128” 需要验证的代理 sudo curl -x “http://username:password192.168.1.2:3128” 1.下载 sudo curl -L "https://github.com/docker/compose/releases/download/1.23.2/docker-compose-$(uname -s)-$(uname -m)" -o /usr/lo…...

3D姿态相关的损失函数
loss_mpjpe: 计算预测3D关键点与真值之间的平均距离误差(MPJPE)。 loss_n_mpjpe: 计算去除尺度后预测3D关键点误差(N-MPJPE),评估结构误差。 loss_velocity: 计算3D关键点的速度/移动的误差,评估运动的平滑程度。 loss_limb_var: 计算肢体长度的方差,引导生成合理的肢体长度…...
ChatGPT取代人类仍然是空想?有没有一种可能是AI在迷惑人类
ChatGPT自从去年发布以来,就掀起了这些大语言模型将如何颠覆一切的激烈讨论,从为学生写作文、输出SEO文章,甚至取代谷歌成为世界上最受欢迎的搜索引擎,影响领域无所不包,甚至可能取代编剧、小说家和音乐家等从事创意工…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
